详解数组的轮转
𝙉𝙞𝙘𝙚!!👏🏻‧✧̣̥̇‧✦👏🏻‧✧̣̥̇‧✦ 👏🏻‧✧̣̥̇:Solitary-walk
⸝⋆ ━━━┓
- 个性标签 - :来于“云”的“羽球人”。 Talk is cheap. Show me the code
┗━━━━━━━ ➴ ⷯ本人座右铭 : 欲达高峰,必忍其痛;欲戴王冠,必承其重。
👑💎💎👑💎💎👑
💎💎💎自💎💎💎
💎💎💎信💎💎💎
👑💎💎 💎💎👑 希望在看完我的此篇博客后可以对你有帮助哟👑👑💎💎💎👑👑 此外,希望各位大佬们在看完后,可以互赞互关一下,看到必回
👑👑👑💎👑👑👑
目录:
一:题目
二:解题思路的分析
三:触类旁通
四:结语
一:题目

二:解题思路的分析
1:暴力求解
1)当 k = 1,要想达到最终结果我们只需要将数组最后一个元素保留,其余元素依次为我的元素 7让道,(依次往后挪动)
2)那么问题又来了,到底是从后往前挪动 还是从前往后挪动数据

当然是从后往前挪动了,你想对了吗???(因为从前往后挪动数据会造成数据的覆盖,全部是数据2)
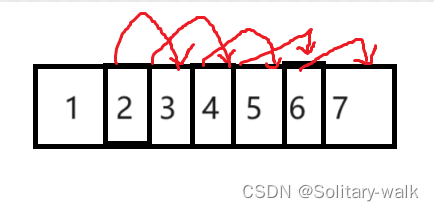

当 k = 2 ,我们直接接着再 k = 1的那个图的基础上进行同样的挪动,这里用循环来实现就可以
void rotate(int* nums, int numsSize, int k)
{k %= numsSize;//避免k的大小超过数组的大小,造成旋转无效 k = 8,numSize = 4,此时不需要轮转//暴力求解// 数组最后一个元素进行保留,其余元素一次后挪动for(int j = 0 ;j<k;j++){int temp = *(nums+numsSize-1);//挪动数据:从后往前挪动for(int i = numsSize-1;i >= 1;i--){*(nums+i) = *(nums+i-1);}*(nums) = temp;}}注意这里有个坑:就是当k大于数组的大小的时候要进行 k对numsSize进行取余,避免无效的旋转
k = 9,这里只需要进行1次旋转就可以
暴力求解对应的事件复杂度是 O(N^2) ,在力扣上是跑不过去的
2: 借助3段逆置
核心思想:
1)先对前 n-k 个元素进行逆置
2)在对后 k 个元素进行逆置
3)最后再对整个数组进行逆置
注意: 以上的顺序不能颠倒;其次就是进行下标传参的时候要仔细
这里我们借助Reverse(int*arr,int lef,int rig)这个函数来进行逆置
void Reverse(int* arr, int lef, int rig)
{while (lef < rig){int tmp = *(arr + lef);//便于进行交换*(arr + lef) = *(arr + rig);*(arr + rig) = tmp;//类似于双指针的思想lef++;rig--;}
}此方法对应的时间复杂度是 O(N),空间复杂度O(1)
三:触类旁通
借助三段逆置的思想实现字符串的逆置
题目:
把字符串 "abcd" 经过2次旋转后实现 "cdab"
前 n - k 对应的

后k对应的
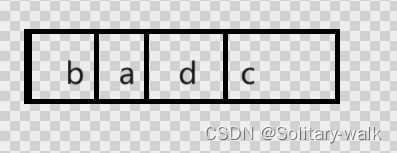
最后整个数组对应的
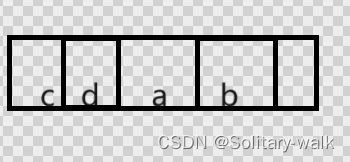
ok~~~话不多说,咱代码见
void Reverse(char* str, int left, int right)
{// 逆置数组while (left < right){int tmp = *(str + left);*(str + left) = *(str + right);*(str + right) = tmp;left++;right--;}
}
void LeftRound3(char* str, int k)
{// 局部旋转 只需进行翻转3次即可//逆置数组 确定下标位置int len = strlen(str);int k = k % len; // 避免无效旋转Reverse(str,0,k - 1);Reverse(str, k,len-1);Reverse(str, 0, len - 1);}结语:以上就是小生今日为大家要share的内容,要是感觉还不错的话,给个关注,咱一波赞走起,看到必回~~~
相关文章:

详解数组的轮转
𝙉𝙞𝙘𝙚!!👏🏻‧✧̣̥̇‧✦👏🏻‧✧̣̥̇‧✦ 👏🏻‧✧̣̥̇:Solitary-walk ⸝⋆ ━━━┓ - 个性标签 - :来于“云”的“羽球人”。…...

html 表格 笔记
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>第二个页面</title><meta name"language" content"cn"> </head> <body><h2 sytle"width:500px;…...
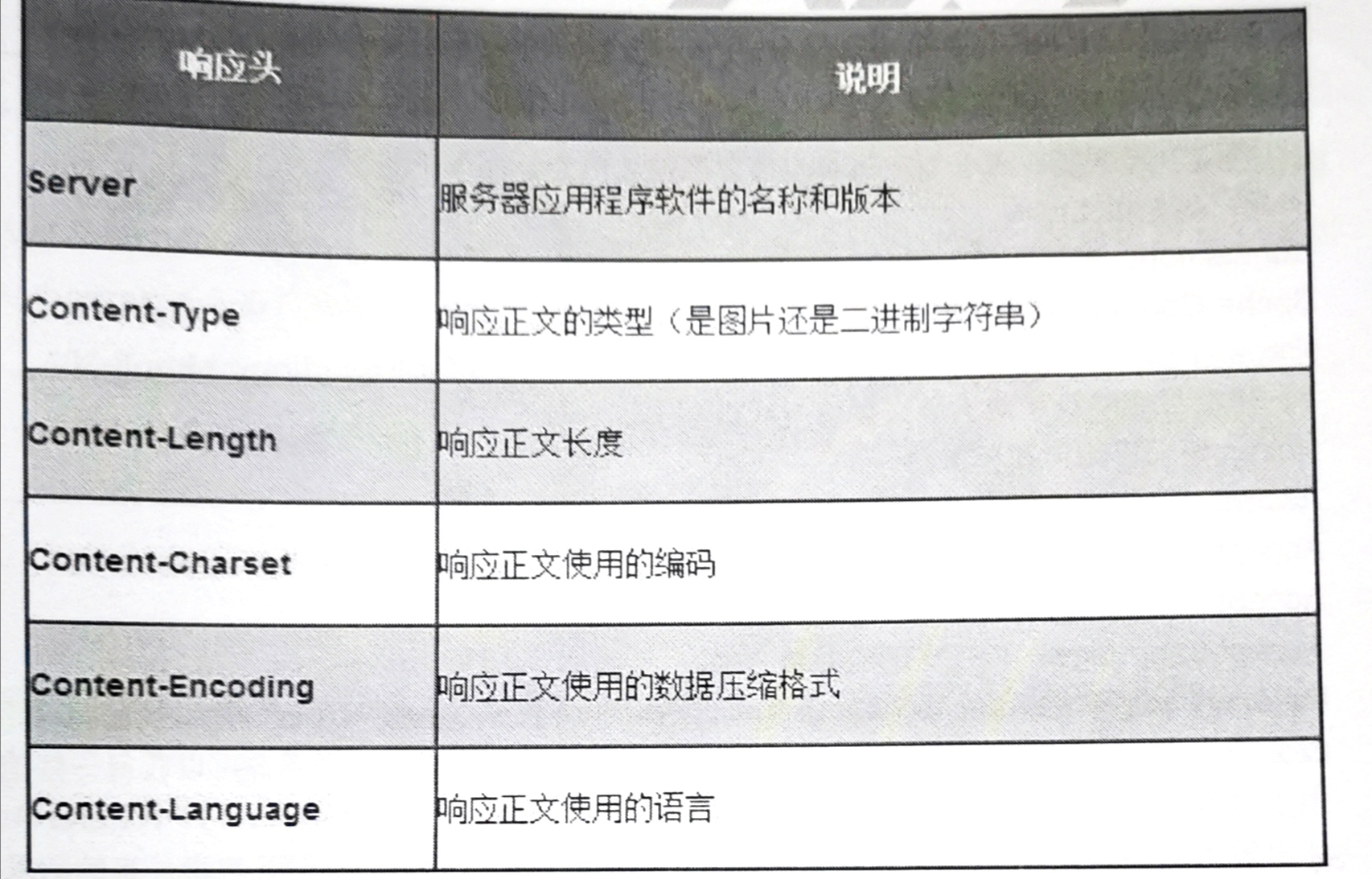
计算机网络【HTTP 面试题】
HTTP的请求报文结构和响应报文结构 HTTP请求报文主要由请求行、请求头、空行、请求正文(Get请求没有请求正文)4部分组成。 1、请求行 由三部分组成,分别为:请求方法、URL以及协议版本,之间由空格分隔;请…...

linux基于用户身份对资源访问进行控制的解析及过程
linux中用户分为三类 1.超级用户(root) 拥有至高无上的权限 2.普通用户 人为创建、权限小,权限受到控制 3.程序用户 运行程序的用户,不是给人使用的,给程序使用的,一般不给登录! 组账…...
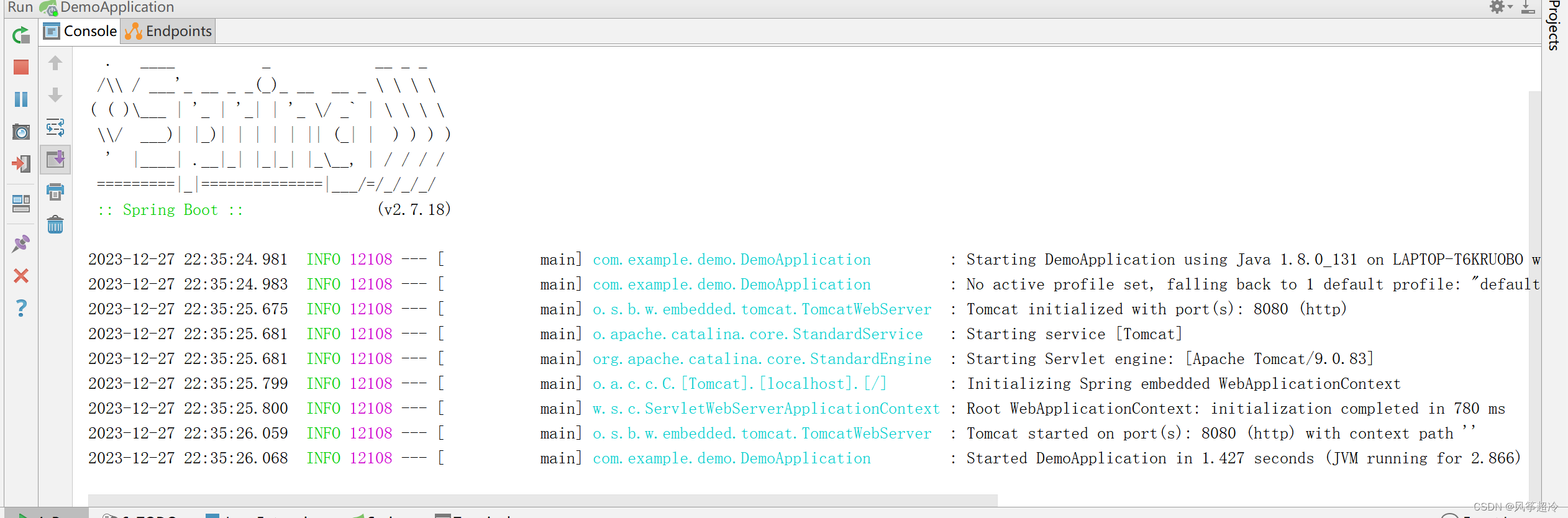
手动创建idea SpringBoot 项目
步骤一: 步骤二: 选择Spring initializer -> Project SDK 选择自己的JDK版本 ->Next 步骤三: Maven POM ->Next 步骤四: 根据JDK版本选择Spring Boot版本 11版本及以上JDK建议选用3.2版本,JDK为11版本…...

【Go语言入门:Go语言的数据结构】
文章目录 3.Go语言的数据结构:3.1. 指针3.2. struct(结构体)3.3. Map(映射,哈希) 3.Go语言的数据结构: 简介: 在Go语言中,数据结构体可以分为四种类型:基础类型、聚合类型、引用类型…...

QT designer的ui文件转py文件之后,实现pycharm中运行以方便修改逻辑,即添加实时模板框架
为PyCharm中的实时模板,你需要遵循以下步骤: 打开PyCharm的设置: 选择 File > Settings(在macOS上是 PyCharm > Preferences)。 导航到实时模板: 在设置中找到 Editor > Live Templates。 添加新的模板组 (可选): 为了…...

什么是负载均衡?
负载均衡是指在计算机网络领域中,将客户端请求分配到多台服务器上以实现带宽资源共享、优化资源利用率和提高系统性能的技术。负载均衡可以帮助小云有效解决单个服务器容量不足或性能瓶颈的问题,小云通过平衡流量负载,使得多台服务器能够共同…...

Python和Java的优缺点
Python的优点: 简单易学:Python的语法简洁清晰,易于学习和理解。丰富的库和框架:Python拥有庞大的标准库和活跃的开源社区,可以快速使用各种功能强大的库和框架,比如NumPy、Pandas、Django等。可读性强&am…...
)
AES - 在tiny-AES-c基础上封装了2个应用函数(加密/解密)
文章目录 AES - 在tiny-AES-c基础上封装了2个应用函数(加密/解密)概述增加2个封装函数的AES库aes.haes.c在官方测试程序上改的测试程序(用来测试这2个封装函数)END AES - 在tiny-AES-c基础上封装了2个应用函数(加密/解密) 概述 在github山有个星数很高的AES的C库 tiny-AES-c …...

51和32单片机读取FSR薄膜压力传感器压力变化
文章目录 简介线性电压转换模块51单片机读取DO接线方式51代码实验效果 32单片机读取AO接线方式32代码实验效果 总结 简介 FSR薄膜压力传感器是可以将压力变化转换为电阻变化的一种传感器,单片机可以读取然后作为粗略测量压力(仅提供压力变化,…...

【maven】pom.xml 文件详解
有关 maven 其他配置讲解参考 maven 配置文件 setting.xml 详解 pom.xml 文件是 Maven 项目的核心配置文件,其中包含了项目的元数据、构建配置、依赖管理等信息。以下是一个 pom.xml 文件的主要部分: <?xml version"1.0" encoding"U…...
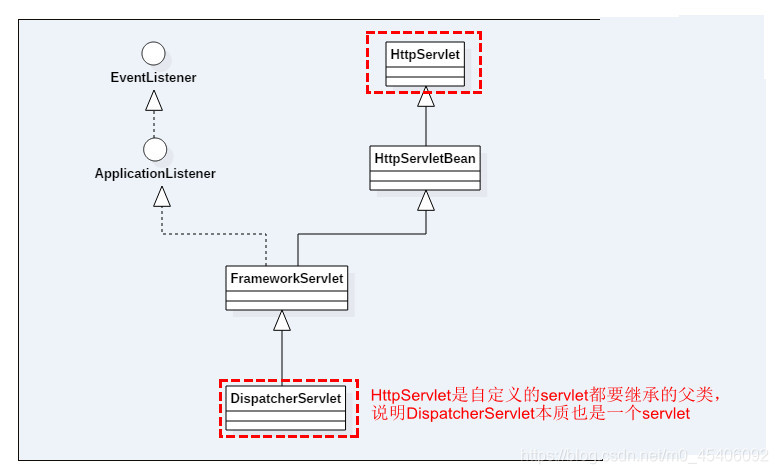
SpringMVC源码解析——DispatcherServlet初始化
在Spring中,ContextLoaderListener只是辅助功能,用于创建WebApplicationContext类型的实例,而真正的逻辑实现其实是在DispatcherServlet中进行的,DispatcherServlet是实现Servlet接口的实现类。Servlet是一个JAVA编写的程序&#…...
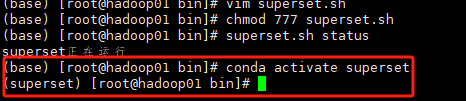
搞定Apache Superset
踩雷了无数次终于解决了Superset的一系列问题 现在是北京时间2023年12月27日,亲测有效。 Superset概述 Apache Superset是一个现代的数据探索和可视化平台。它功能强大且十分易用,可对接各种数据源,包括很多现代的大数据分析引擎ÿ…...

【每日试题】java面试之ssm框架
以下是20道常见的SSM(SpringSpring MVCMyBatis)面试题目和答案: 什么是SSM框架? SSM是指SpringSpring MVCMyBatis的组合,它是Java Web开发中常用的轻量级框架集合。 介绍一下SSM框架各个组件的作用? Sprin…...

Flutter 疑难杂症集合
一. Flutter集成uni小程序sdk 1. 手机连接电脑测试打开uni小程序没问题,打包成apk后debug编译下的apk也没问题,但就是release编译的apk包打不开小程序。 报错情景:点击后页面会闪现一下黑色的背景,然后又跳转回了点击之前的页面。…...

PHP序列化总结1--序列化和反序列化的基础知识
序列化和反序列化的作用 1.序列化:将对象转化成数组或者字符串的形式 2.反序列化:将数组或字符串的形式转化为对象 为什么要进行序列化 这种数据形式中间会有很多空格,不同人有不同的书写情况,可能还会出现换行的情况 为此为了…...

【Linux】 last 命令使用
last 命令 用于检索和展示系统中用户的登录信息。它从/var/log/wtmp文件中读取记录,并将登录信息按时间顺序列出。 著者 Miquel van Smoorenburg 语法 last [-R] [-num] [ -n num ] [-adiox] [ -f file ] [name...] [tty...]last 命令 -Linux手册页 选项及作用…...

Git 分布式版本控制系统(序章1)
第一章 Git 分布式版本控制系统 为什么学Git? 某些企业面试需要掌握Git,同时,也方便管理自己的Qt项目。 一、Git 客户端下载(Windows) 下载地址 https://gitee.com/all-about-git#git-%E5%A4%A7%E5%85%A8 二、Git 的特点 分支…...

给WordPress网站添加返回顶部按钮
给WordPress网站底部添加一个按钮,点它就可以现实快速返回到顶部。有两种方法可以现实,一种是通过安装相关插件来实现。另外一种方式就是以纯属代码的方式来实现。 给WordPress网站底部添加一个按钮,点它就可以现实快速返回到顶部。有两种方…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...



