目标检测损失函数:IoU、GIoU、DIoU、CIoU、EIoU、alpha IoU、SIoU、WIoU原理及Pytorch实现
前言
损失函数是用来评价模型的预测值和真实值一致程度,损失函数越小,通常模型的性能越好。不同的模型用的损失函数一般也不一样。损失函数主要是用在模型的训练阶段,如果我们想让预测值无限接近于真实值,就需要将损失值降到最低,在这个过程中就需要引入损失函数,而损失函数的选择又是十分关键。尤其是在目标检测中,损失函数直接关乎到检测效果是否准确,其中IOU损失函数目前主要应用于目标检测的领域,其演变的过程如下:IOU --> GIOU --> DIOU -->CIOU损失函数,每一种损失函数都较上一种损失函数有所提升,下面来具体介绍这几种损失函数。
1 IoU(Intersection over Union)
1.1 IoU简介
UnitBox: An Advanced Object Detection Network
IoU全称Intersection over Union,交并比。IoU是一种测量在特定数据集中检测相应物体准确度的一个标准。只要是在输出中得出一个预测范围(bounding boxes)的任务都可以用IoU来进行测量。
IoU算法是使用最广泛的算法,大部分的检测算法都是使用的这个算法。在目标识别中,我们的预测框与实际框的某种比值就是IoU。

1.2 IoU公式
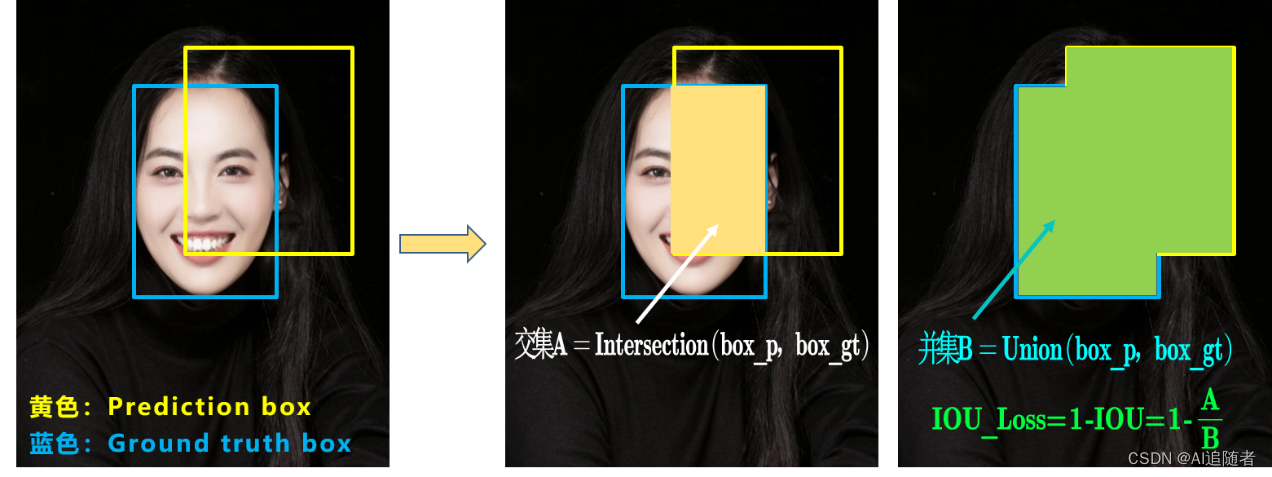
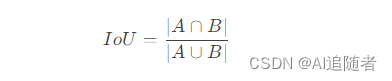
1.3 优点
- IOU能够直观地反映出目标检测结果与真实情况之间的匹配程度。
- IOU具有尺度不变性,由于IOU是基于重叠度量的,它不受目标尺度和形状变换的影响,这使得IOU适用于各种不同尺度和形状的目标检测任务。
1.4 缺点
- 当预测框和目标框不相交时,即IOU=0时,不能反映两个目标之间距离的远近,此时损失函数不可导,IOU Loss 无法优化。
- 当两个检测框大小相同,两个IOU也相同,IOU_Loss无法精确的反映两个框的重合度大小。

1.5 IoU代码
def IoU(box1, box2):b1_x1, b1_y1, b1_x2, b1_y2 = box1b2_x1, b2_y1, b2_x2, b2_y2 = box2xx1 = np.maximum(b1_x1, b2_x1)yy1 = np.maximum(b1_y1, b2_y1)xx2 = np.minimum(b1_x2, b2_x2)yy2 = np.minimum(b1_y2, b2_y2)w = np.maximum(0.0, yy2 - yy1)h = np.maximum(0.0, xx2 - xx1)inter = w * hIoU = inter/((b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - inter)print("IoU: ", IoU)if __name__ == "__main__":box1 = np.array([100, 100, 210, 210])box2 = np.array([150, 150, 230, 220])IoU(box1, box2)2 GIoU
Generalized Intersection over Union: A Metric and A Loss for Bounding BoxRegression
2.1 GIoU简介
通过上述分析,当预测框和真实框不相交时IoU值为0,导致很大范围内损失函数没有梯度。针对这一问题,提出了GIoU作为损失函数。GIoU比IoU多了一个‘Generalized’,能在更广义的层面上计算IoU。当检测框和真实框没有出现重叠的时候IoU的loss都是一样的,因此GIoU就引入了最小封闭形状C(C可以把A,B包含在内),在不重叠情况下能让预测框尽可能朝着真实框前进,这样就可以解决检测框和真实框没有重叠的问题 。
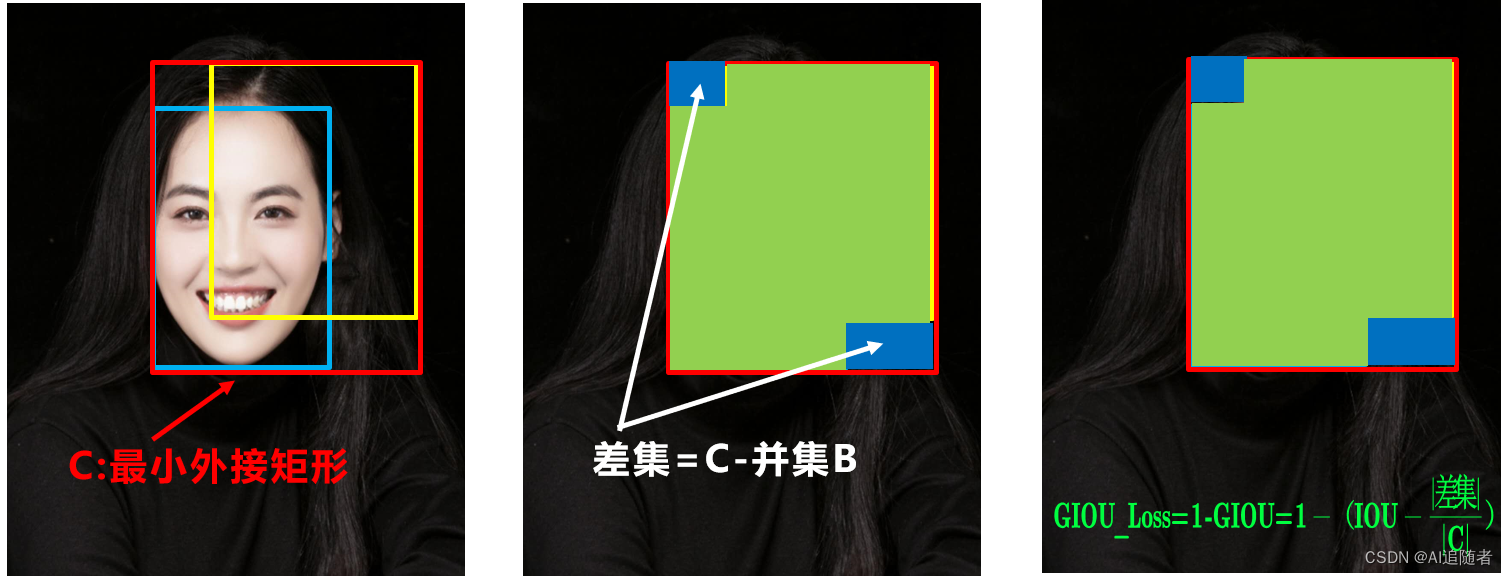
2.2 GIoU公式
算法公式及其解释:其实想法也很简单(但这一步很难):假如现在有两个box A,B,我们找到一个最小的封闭形状C,让C可以把A,B包含在内,然后再计算C中没有覆盖A和B的面积占C总面积的比值,最后用A与B的IoU减去这个比值,GIoU计算公式如下
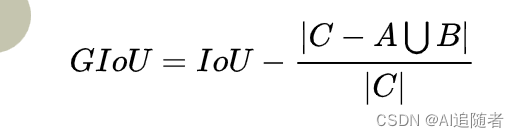
2.3 优点
- GIOU_Loss中,增加了相交尺度的衡量方式,缓解了单纯IOU_Loss时的尴尬,但是依然没有完全解决IoU存在的问题
2.4 缺点
- 对每个预测框与真实框均要去计算最小外接矩形,计算及收敛速度受到限制
- 状态1、2、3都是预测框在目标框内部且预测框大小一致的情况,这时预测框和目标框的差集都是相同的,因此这三种状态的GIoU值也都是相同的,这时GIoU退化成了IoU,无法区分相对位置关系。

2.5 GIoU代码
def GIoU(box1, box2):b1_x1, b1_y1, b1_x2, b1_y2 = box1b2_x1, b2_y1, b2_x2, b2_y2 = box2# IOUxx1 = np.maximum(b1_x1, b2_x1)yy1 = np.maximum(b1_y1, b2_y1)xx2 = np.minimum(b1_x2, b2_x2)yy2 = np.minimum(b1_y2, b2_y2)inter_w = np.maximum(0.0, yy2 - yy1)inter_h = np.maximum(0.0, xx2 - xx1)inter = inter_w * inter_hUnion = (b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - inter# GIOUC_xx1 = np.minimum(b1_x1, b2_x1)C_yy1 = np.minimum(b1_y1, b2_y1)C_xx2 = np.maximum(b1_x2, b2_x2)C_yy2 = np.maximum(b1_y2, b2_y2)C_area = (C_xx2 - C_xx1) * (C_yy2 - C_yy1)IOU = inter / UnionGIOU = IOU - abs((C_area-Union)/C_area)print("GIOU:", GIOU)if __name__ == "__main__":box1 = np.array([100, 100, 210, 210])box2 = np.array([150, 150, 230, 220])GIoU(box1, box2)3 DIoU
Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
3.1 简介
好的目标框回归函数应该考虑三个重要几何因素:重叠面积、中心点距离,长宽比。针对IoU和GIoU存在的问题,作者从两个方面进行考虑
- 一:如何最小化预测框和目标框之间的归一化距离?
- 二:如何在预测框和目标框重叠时,回归的更准确?
针对第一个问题,提出了DIoU_Loss(Distance_IoU_Loss),从而使收敛速度更快,性能更好。
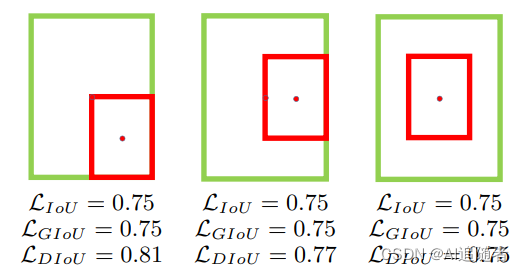
3.2 DIoU公式
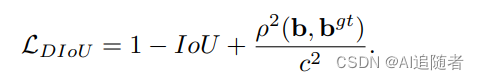
其中,,
分别表示预测框和真实框的中心点,且
表示两个中心点间的欧式距离,
表示能够同时包含预测框和真实框的最小闭包区域的对角线距离。

3.3 优点
- DIOU在与目标框重叠时,仍然可以为边界框提供移动方向;
- DIOU可以直接最小化两个目标框的距离,因此比GIOU收敛快得多;
- DIOU还可以替换普通的IOU评价策略,应用于NMS中,使得NMS得到的结果更加合理和有效。
3.4 缺点
- DIoU考虑了重叠面积和中心点距离,当目标框包裹预测框的时候,直接度量2个框的距离,因此DIoU收敛的更快,但并没有考虑到长宽比。
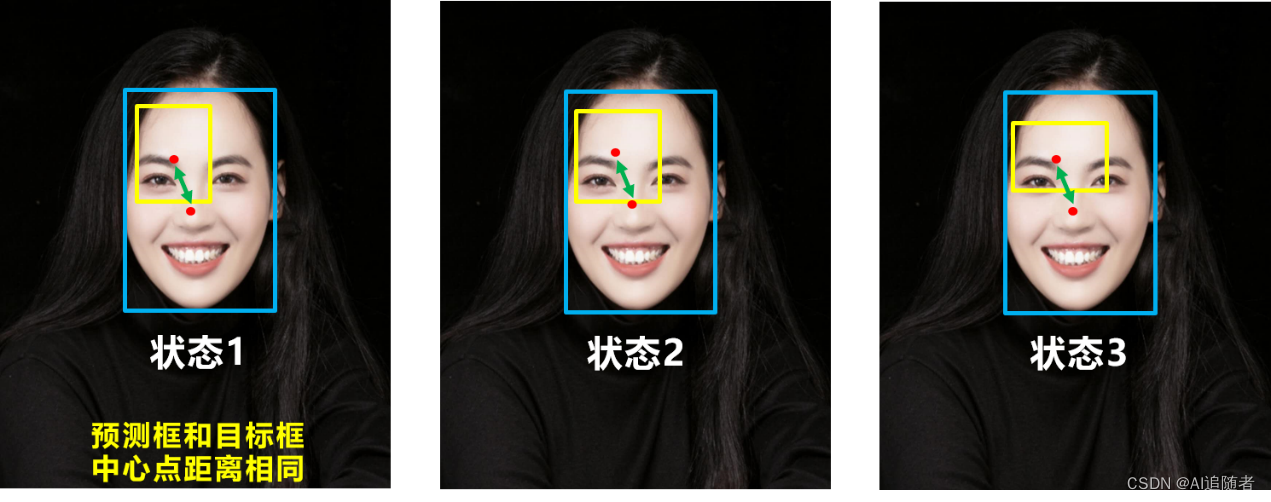
比如上面三种情况,目标框包裹预测框,本来DIOU_Loss可以起作用。但预测框的中心点的位置都是一样的,因此按照DIOU_Loss的计算公式,三者的值都是相同的。
3.5 DIoU代码
def DIoU(box1, box2):b1_x1, b1_y1, b1_x2, b1_y2 = box1b2_x1, b2_y1, b2_x2, b2_y2 = box2# IOUxx1 = np.maximum(b1_x1, b2_x1)yy1 = np.maximum(b1_y1, b2_y1)xx2 = np.minimum(b1_x2, b2_x2)yy2 = np.minimum(b1_y2, b2_y2)inter_w = np.maximum(0.0, xx2 - xx1)inter_h = np.maximum(0.0, yy2 - yy1)inter = inter_w * inter_hUnion = (b1_x2 - b1_x1)*(b1_y2 - b1_y1) + (b2_x2 - b2_x1)*(b2_y2 - b2_y1) - inter# DISTANCEC_xx1 = np.minimum(b1_x1, b2_x1)C_yy1 = np.minimum(b1_y1, b2_y1)C_xx2 = np.maximum(b1_x2, b2_x2)C_yy2 = np.maximum(b1_y2, b2_y2)C_area = (C_xx2 - C_xx1) * (C_yy2 - C_yy1)center_b_x = (b1_x1+b1_x2)/2center_b_y = (b1_y1+b1_y2)/2center_gtb_x = (b2_x1+b2_x2)/2center_gtb_y = (b2_y1+b2_y2)/2center_distance = (center_gtb_x-center_b_x)**2 + (center_gtb_y-center_b_y)**2c_distance = (C_xx2 - C_xx1)**2 + (C_yy2 - C_yy1)**2IOU = inter/UnionDIOU = IOU - center_distance /c_distanceprint("DIOU:", DIOU)if __name__ == "__main__":box1 = np.array([100, 100, 210, 210])box2 = np.array([150, 150, 230, 220])DIoU(box1, box2)4 CIoU
Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
4.1 简介
DIoU考虑了重叠面积和中心点距离,当目标框包裹预测框的时候,直接度量2个框的距离,因此DIoU收敛的更快,但并没有考虑到长宽比。针对这个问题,又提出了CIOU_Loss,不对不说,科学总是在解决问题中,不断进步!!
CIoU就是在DIoU的基础上增加了检测框尺度的loss,增加了长和宽的loss,使得目标框回归更加稳定,不会像IoU和GIoU一样出现训练过程中发散等问题。
4.2 CIoU公式
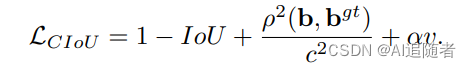
是用来衡量长宽比一致性的参数,
定义如下:
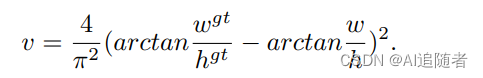
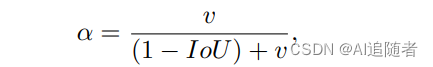
4.3 优点
- 形状不变性: CIOU 损失函数在设计上考虑了目标框的形状信息,通过引入修正因子,使得损失对于不同形状的目标框更具鲁棒性。这使得模型更容易捕捉目标的准确形状。
- 对定位精度的敏感性: CIOU 损失函数对目标框的位置预测更为敏感,因为它考虑了目标框的对角线距离。这有助于提高目标检测模型在定位目标时的精度。
- 全面性: CIOU 损失函数综合考虑了位置、形状和方向等多个因素,使得模型更全面地学习目标框的特征。这有助于提高模型在复杂场景中的性能。
4.4 缺点
- 如果预测框和gt框的长宽比是相同的,那么长宽比的惩罚项恒为0,不合理
- 观察CIoU中w, h相对于v的梯度,发现这两个梯度是一对相反数,也就是说,w和h不能同时增大或减小,这显然也不够合理的。
4.5 代码
def CIoU(box1, box2):b1_x1, b1_y1, b1_x2, b1_y2 = box1b2_x1, b2_y1, b2_x2, b2_y2 = box2# IOUxx1 = np.maximum(b1_x1, b2_x1)yy1 = np.maximum(b1_y1, b2_y1)xx2 = np.minimum(b1_x2, b2_x2)yy2 = np.minimum(b1_y2, b2_y2)inter_w = np.maximum(0.0, xx2 - xx1)inter_h = np.maximum(0.0, yy2 - yy1)inter = inter_w*inter_hUnion = (b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - interIOU = inter/UnionC_xx1 = np.minimum(b1_x1, b2_x1)C_yy1 = np.minimum(b1_y1, b2_y1)C_xx2 = np.maximum(b1_x2, b2_x2)C_yy2 = np.maximum(b1_y2, b2_y2)# DISTANCEcenter_b_x = (b1_x1 + b1_x2)/2center_b_y = (b1_y1 + b1_y2)/2center_gtb_x = (b2_x1 + b2_x2)/2center_gtb_y = (b2_y1 + b2_y2)/2C_area = (C_xx2-C_xx1)*(C_yy2-C_yy1)Distance = (center_gtb_x-center_b_x)**2 + (center_gtb_y-center_b_y)**2Distance_area = Distance/C_area**2# aspect ratiopred_w = b1_y2 - b1_y1pred_h = b1_x2 - b1_x1gt_w = b2_y2 - b2_y1gt_h = b2_x2 - b2_x1v = (4/(np.pi)**2)*(np.arctan(gt_w/gt_h) - np.arctan(pred_w/pred_h))**2alpha = v/((1-IOU) + v)CIOU = IOU - Distance_area - alpha*vprint("CIOU:", CIOU)if __name__ == "__main__":box1 = np.array([100, 100, 210, 210])box2 = np.array([150, 150, 230, 220])CIoU(box1, box2)相关文章:
目标检测损失函数:IoU、GIoU、DIoU、CIoU、EIoU、alpha IoU、SIoU、WIoU原理及Pytorch实现
前言 损失函数是用来评价模型的预测值和真实值一致程度,损失函数越小,通常模型的性能越好。不同的模型用的损失函数一般也不一样。损失函数主要是用在模型的训练阶段,如果我们想让预测值无限接近于真实值,就需要将损失值降到最低…...

今年努力输出的嵌入式Linux视频
今年努力了一波,几个月周六日无休,自己在嵌入式linux工作有些年头,结合自己也是一直和SLAM工程师对接,所以输出了一波面向SLAM算法工程师Linux课程,当然嵌入式入门的同学也可以学习。下面是合作的官方前面发的宣传文章…...

python非常好用的文件系统监控库
如果你不想使用Watchdog库,而是自己编写代码来监视文件系统的变化,可以使用Python的内置模块os和time来实现。 下面是一个简单的示例代码,演示如何使用os和time模块来监视文件系统中文件的变化: pythonimport osimport timedef m…...

基于SpringBoot的电影购票系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的电影购票系统,java项目…...

Spring系列:Spring如何解决循环依赖
❤ 作者主页:欢迎来到我的技术博客😎 ❀ 个人介绍:大家好,本人热衷于Java后端开发,欢迎来交流学习哦!( ̄▽ ̄)~* 🍊 如果文章对您有帮助,记得关注、点赞、收藏、…...
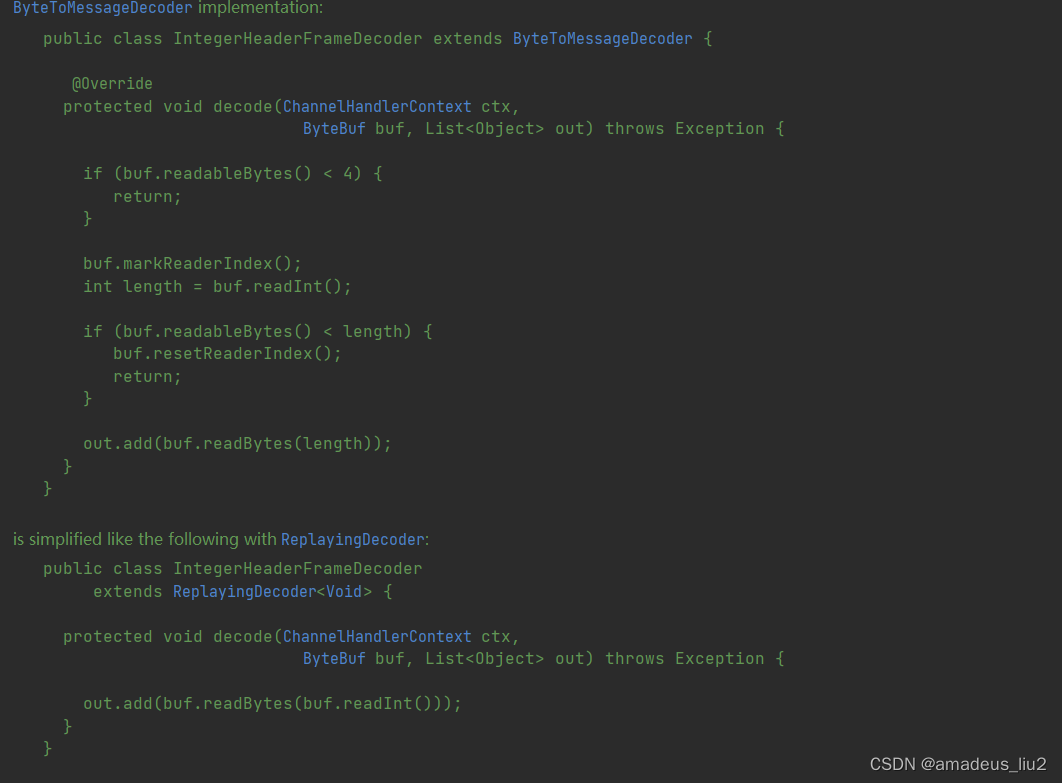
netty源码:(40)ReplayingDecoder
ReplayingDecoder是ByteToMessageDecoder的子类,我们继承这个类时,也要实现decode方法,示例如下: package cn.edu.tju;import io.netty.buffer.ByteBuf; import io.netty.channel.ChannelHandlerContext; import io.netty.handle…...

Apache Doris (五十五): Doris Join类型 - Colocation Join
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹哥教你大数据个人主页-哔哩哔哩视频 目录 1. Colocation Join原理...
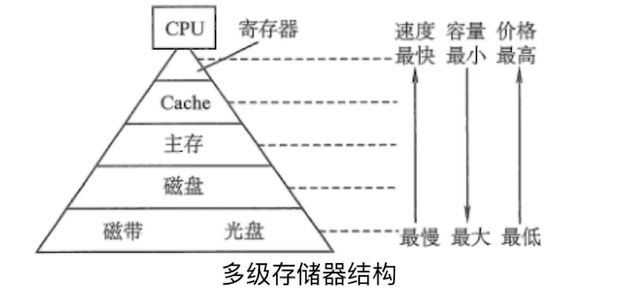
计算机组成原理复习7
内存管理 文章目录 内存管理存储器概述存储器的分类按在计算机中的作用(层次)分类按存储介质分类按存取方式分类按信息的可保存性分类 存储器的性能指标存储容量单位成本存储速度:数据传输率数据的宽度/存储周期 存储器的层次化结构多级存储系…...

python使用openpyxl操作excel
文章目录 前提读取已有excel创建一个excel工作簿对象创建excel工作簿中的工作表获取工作表第一种:.active 方法第二种:通过工作表名获取指定工作表第三种:.get_sheet_name() 修改工作表的名称数据操作写入数据按单元格写入通过指…...
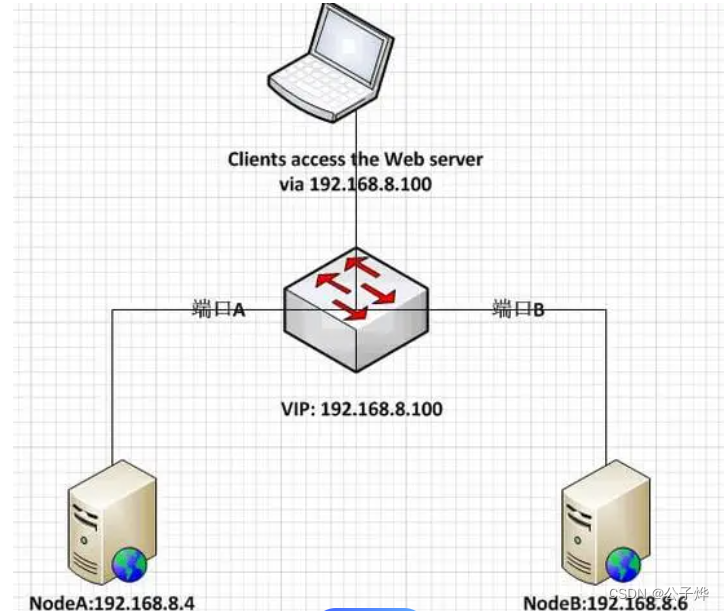
使用keepalived时虚拟IP漂移注意事项
什么是Keepalived服务 keepalived是一个开源的软件项目,用于实现高可用性(HA)的网络服务器负载均衡和故障转移。它允许将多台服务器组合在一起,形成一个虚拟服务器集群,实现负载均衡和故障转移。 keepalived的核心功…...
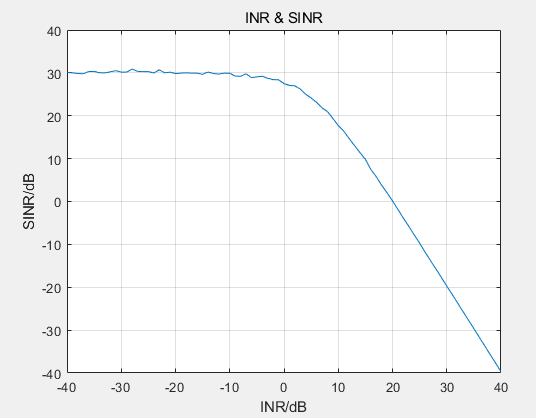
32阵元 MVDR和DREC DOA估计波束方向图对比
32阵元 MVDR和DREC DOA估计波束方向图对比 一、原理 MVDR原理:https://zhuanlan.zhihu.com/p/457528114 DREC原理(无失真响应特征干扰相消器):http://radarst.ijournal.cn/html/2019/3/201903018.html 主要参数: 阵…...
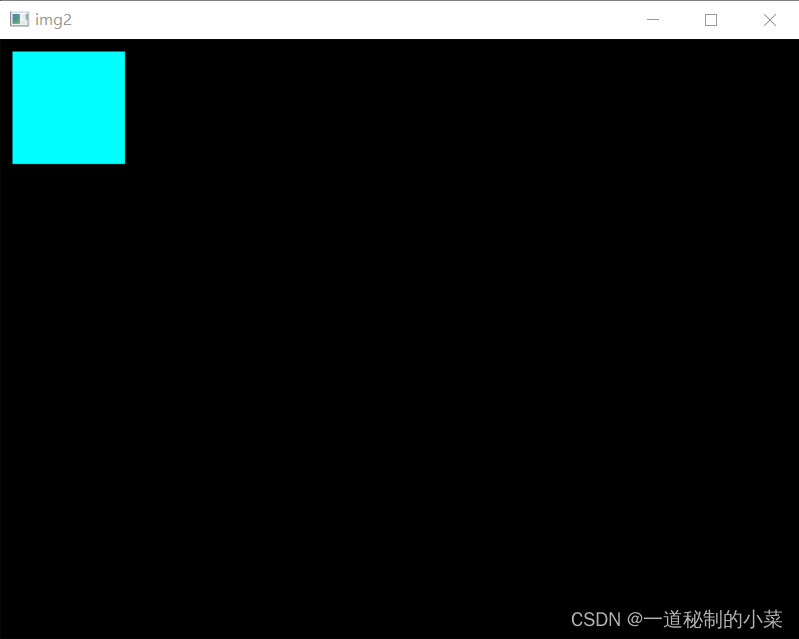
OpenCV-11颜色通道的分离与合并
本次我们使用两个比较重要的API split(mat)将图像的通道进行分割。 merge((ch1,ch2,ch3))将多个通道进行融合。 示例代码如下: import cv2 import numpy as npimg np.zeros((480, 640, 3),…...

从0到1入门C++编程——01 C++基础知识
文章目录 一、工具安装二、新建项目三、设置字体、注释、行号四、C基础知识1.数据类型2.输入输出3.运算符4.选择、循环结构5.跳转语句6.数组7.函数8.指针9.结构体 一、工具安装 学习C使用到的工具是Visual Studio,Visual Studio 2010旗舰版下载链接:点此…...

C#编程-编写和执行C#程序2
C#编程-编写和执行C#程序 问题陈述 Dvid所在的团队正在为网球比赛开发自动排名软件。他负责创建一个程序来接受网球选手的以下详细信息并将其显示在屏幕上: 1.姓名 2.排名 您需要帮助David创建该程序。 要创建所需的程序,David需要执行以下步骤: 1.打开“记事本”。 2.在“…...

Day02-ES6
一.proxy代理 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title> </head>…...

2023年12月记录内容管理
文章目录 前言1.[vue构建项目](https://mp.csdn.net/mp_blog/creation/editor/134829688)2. [Nodejs后端express框架](https://mp.csdn.net/mp_blog/creation/editor/134841711)3. [前端知识点](https://mp.csdn.net/mp_blog/creation/editor/132810879)4.[前端知识点-vue篇&am…...
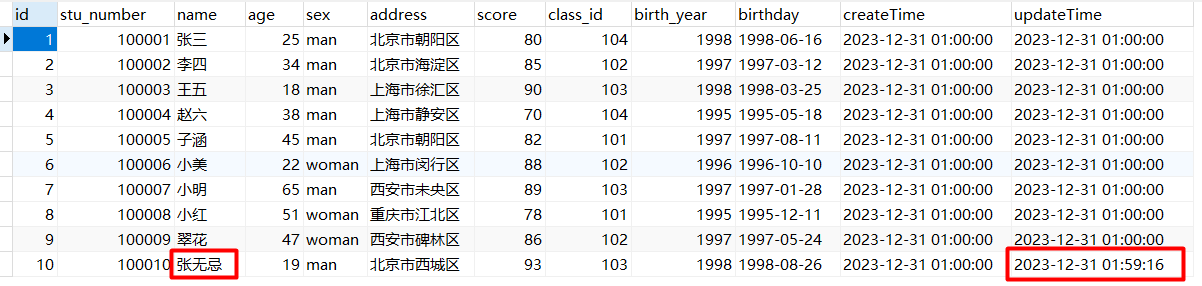
【测试基础】构造测试数据之 MySQL 篇
构造测试数据之 MySQL 篇 作为一名测试工程师,我们经常会构造测试数据进行一些功能验证。为了暴露更多的问题,在测试数据的构造上,我们应该尽可能的构造不同类型字段的数据,且一张表的字段最好不低于 10 10 10 个。 对于 MySQL …...

基于单片机的语音识别自动避障小车(论文+源码)
1.系统设计 此次基于单片机的语音识别自动避障小车,以STC89C52单片机作为系统的主控制器,利用超声波模块来实现小车与障碍物距离的测量并通过LCD液晶显示,当距离低于阈值时会通过WT588语音模块进行报警提示,并且小车会后退来躲避…...
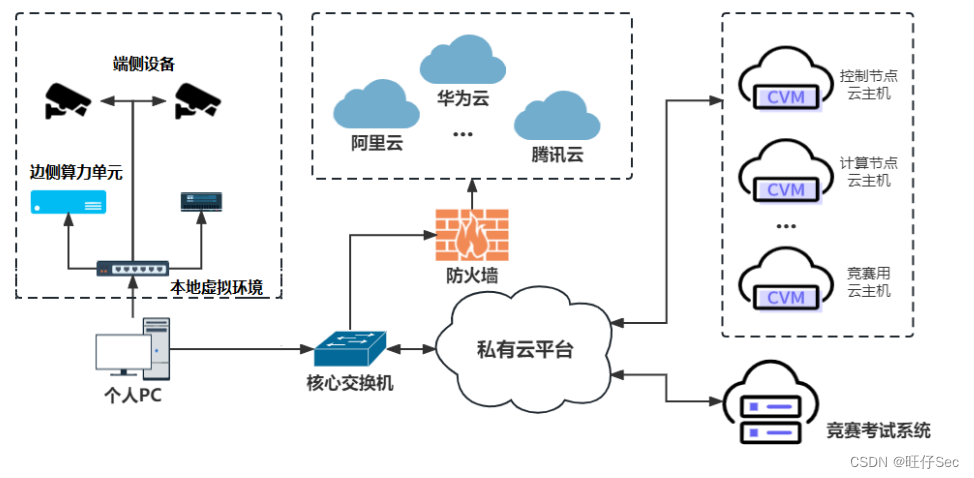
2023年“中银杯”四川省职业院校技能大赛“云计算应用”赛项样题卷①
2023年“中银杯”四川省职业院校技能大赛“云计算应用”赛项(高职组) 样题(第1套) 目录 2023年“中银杯”四川省职业院校技能大赛“云计算应用”赛项(高职组) 样题(第1套) 模块一…...
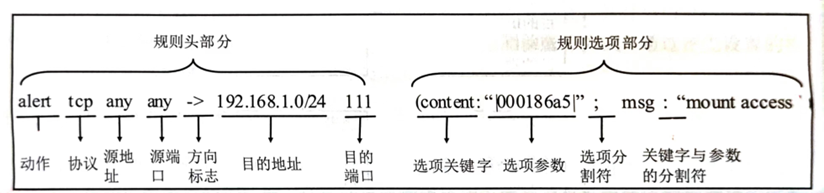
【信息安全原理】——入侵检测与网络欺骗(学习笔记)
📖 前言:在网络安全防护领域,防火墙是保护网络安全的一种最常用的设备。网络管理员希望通过在网络边界合理使用防火墙,屏蔽源于外网的各类网络攻击。但是,防火墙由于自身的种种限制,并不能阻止所有攻击行为…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
