线性代数基础知识
计算机视觉一些算法中常会用到线性代数的一些知识，为了便于理解和快速回忆，博主这边对常用的一些知识点做下整理，主要来源于如下这本书籍。
1. 矩阵不仅仅是数字排列而已，不然也不会有那么大精力研究它。其可以表示一种映射
关于映射，变换的一些帖子可以参考如下的
仿射变换（AffineTransform）与仿射矩阵-CSDN博客
图像的仿射变换 - 知乎
https://www.cnblogs.com/bnuvincent/p/6691189.html
2. 矩阵即是映射
3. 矩阵的运算
4.矩阵的逆
5.行列式
.
行列式计算也可参考其它帖子
行列式10种计算方法！几何及线代必考知识点梳理！ - 知乎
线性代数行列式知识点总结
线代学习笔记（7）- 行列式 - 知乎
6. 逆矩阵的计算
求逆矩阵的三种方法
计算逆矩阵的三种方法_矩阵求逆公式-CSDN博客
7. 初等变换
矩阵的初等变换 - 知乎
百度安全验证
8. 线性方程组的解
高斯-若尔当消元法_百度百科
线性代数的学习和整理14: 线性方程组求解的3种方法，重点讲矩阵函数求解-CSDN博客
矩阵基础4-线性方程组详解 - 简书
齐次线性方程组_百度百科
https://jingyan.baidu.com/article/fec7a1e5cb631f1190b4e732.html
线代-3.非齐次线性方程组解法 - 知乎
齐次和非齐次线性方程组的解法(整理定稿)
9. 单射，满设，双射
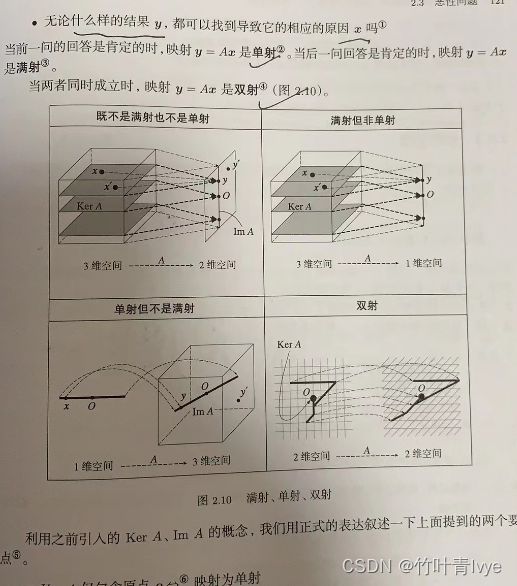
10. 矩阵的秩
一些关于矩阵秩的总结 - 知乎
DAY46|线代『矩阵』核心考点：矩阵的秩
如何理解矩阵的「秩」？
解的关系所确定的系数矩阵秩的关系 - 知乎
11.2 齐次线性方程组的基础解系和通解 - 知乎
11. 特征值和特征向量
线性代数的本质(10)-特征值与特征向量 - 知乎
11.3 求解特征值和特征向量（基础解系法） - 知乎
12. 矩阵对角化
12.2 对称矩阵的正交对角化 - 知乎
什么样的矩阵可以对角化？ - 知乎
对角化_百度百科
13. 相似性矩阵
相似矩阵_百度百科
怎么证明两个矩阵相似？ - 知乎
百度安全验证
如何证两矩阵相似 - 知乎
“拨开迷雾”，如何判定矩阵相似？ - 知乎
线性代数（相似矩阵） - 知乎
14. Jordan标准型
矩阵分析：特征值，相似度对角化，Jordan标准形_jordan标准型和特征值的关系-CSDN博客
Jordan标准型_百度百科
15. 正定矩阵
浅谈「正定矩阵」和「半正定矩阵」
矩阵理论| 特殊矩阵：正定矩阵-CSDN博客
MIT—微分方程与线性代数笔记7.2 正定矩阵 - 知乎
·16.正交矩阵
14、范数、内积、归一、正交化、标准正交(Schmidt化） - 知乎
线性代数（正交矩阵） - 知乎
线性代数（正交矩阵） - 知乎
正交规范化、正交矩阵_矩阵正交规范化-CSDN博客
如何理解施密特（Schmidt）正交化 - 知乎
正交矩阵的几何意义是什么？ - 知乎
17.矩阵和坐标系变换的关系
浅谈矩阵乘法与坐标系变换 - 知乎
一些关于矩阵秩的总结 - 知乎’
矩阵与坐标系的映射关系_矩阵坐标-CSDN博客
矩阵变换坐标系 深入理解 - 知乎
线性代数（三）：坐标变换 - 知乎
18.奇异值分解
SVD-矩阵奇异值分解 —— 原理与几何意义 - 知乎
百度安全验证
奇异值分解（SVD）原理总结
《统计学习方法》之SVD - 知乎
基础算法-奇异值分解SVD_右奇异向量-CSDN博客
线性代数的本质(10)-特征值与特征向量 - 知乎
19.常见矩阵
线性代数导学（八）： 那些常见且特殊的矩阵与其目的 - 知乎
20.LU分解
LU分解 - 知乎
lu分解有什么意义啊？ - 知乎
相关文章：
线性代数基础知识
计算机视觉一些算法中常会用到线性代数的一些知识，为了便于理解和快速回忆，博主这边对常用的一些知识点做下整理，主要来源于如下这本书籍。 1. 矩阵不仅仅是数字排列而已，不然也不会有那么大精力研究它。其可以表示一种映射 关于…...
Linux Shell 016-文本比较工具diff
Linux Shell 016-文本比较工具diff 本节关键字：Linux、Bash Shell、文本比较 相关指令：diff、cat、patch diff介绍 diff工具用于逐行比较文件的不同，如果指定要比较目录，则diff会比较目录中相同文件名的文件，但不会…...
八股文打卡day13——计算机网络（13）
面试题：DNS是什么？DNS的查询过程是什么？ 我的回答： 我来讲一下我对DNS的理解 DNS是域名系统，它是一个域名和IP地址相互映射的数据库。通过DNS，可以将我们浏览器中输入的域名，例如：…...
android studio导入module
在Android Studio中导入一个Module（模块），可以按照以下步骤进行操作： 打开Android Studio，并打开你的项目。在菜单栏中，点击 "File"（文件）-> "New"…...
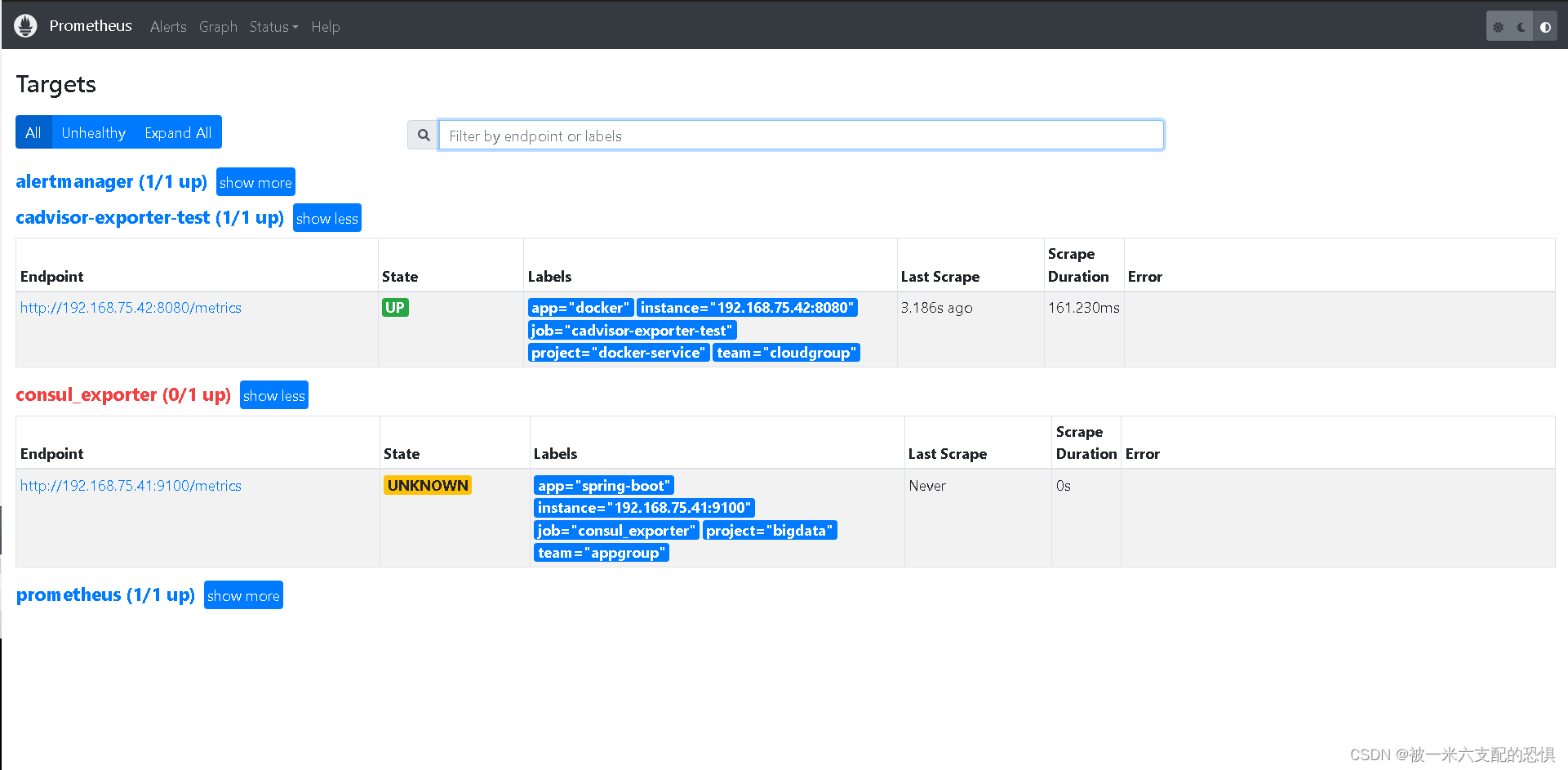
Prometheus通过consul实现自动服务发现
环境,软件准备 本次演示环境，我是在虚拟机上安装 Linux 系统来执行操作，以下是安装的软件及版本： System: CentOS Linux release 7.6Docker: 24.0.5Prometheus: v2.37.6Consul: 1.6.1 注意：这里为了方便启动 Prometheus、Consul服…...
c++11--原子操作，顺序一致性，内存模型
1.原子操作 多线程下为了实现对临界区资源的互斥访问，最普遍的方式是使用互斥锁保护临界区。 然而，如果临界区资源仅仅是数值类型时，对这些类型c提供了原子类型，通过使用原子类型可以更简洁的获得互斥保护的支持。 (1). 一个实例…...
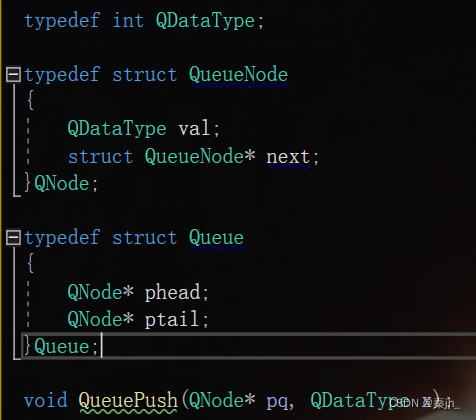
【数据结构】栈和队列（队列的基本操作和基础知识）
🌈个人主页：秦jh__https://blog.csdn.net/qinjh_?spm1010.2135.3001.5343🔥 系列专栏：《数据结构》https://blog.csdn.net/qinjh_/category_12536791.html?spm1001.2014.3001.5482 目录 前言 队列 队列的概念和结构 队列的…...
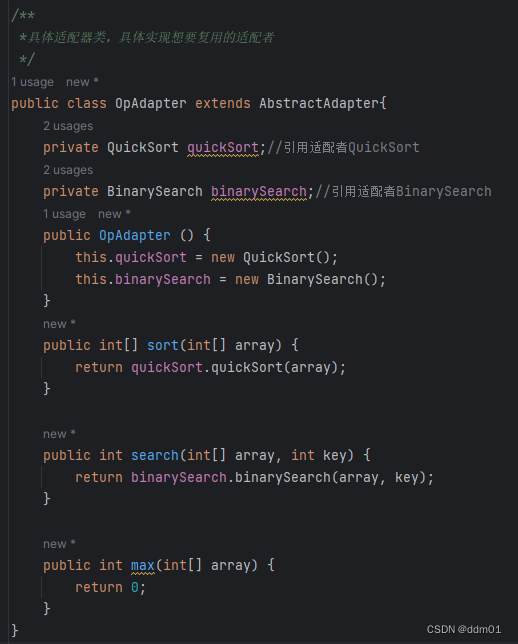
设计模式——适配器模式（Adapter Pattern）
概述 适配器模式可以将一个类的接口和另一个类的接口匹配起来，而无须修改原来的适配者接口和抽象目标类接口。适配器模式(Adapter Pattern)：将一个接口转换成客户希望的另一个接口，使接口不兼容的那些类可以一起工作，其别名为包装…...
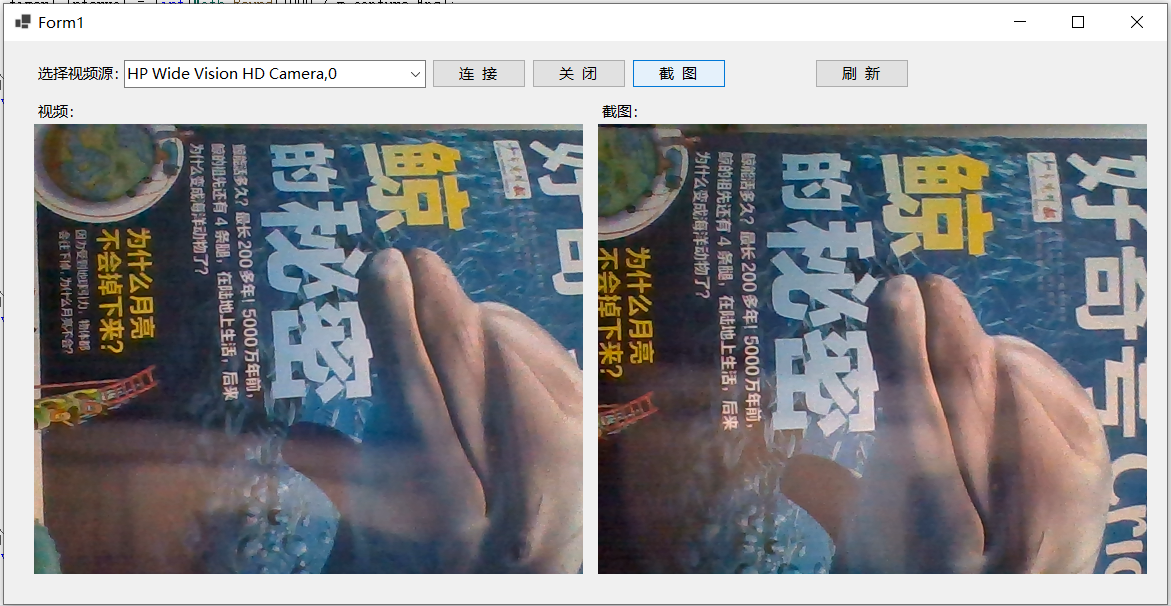
测试C#使用OpenCvSharp从摄像头获取图片
OpenCvSharp也支持获取摄像头数据，不同于之前测试AForge时使用AForge控件显示摄像头数据流并从中截图图片，OpenCvSharp中显示摄像头数据流需要周期性地从摄像头中截取图片并显示在指定控件中。本文学习C#使用OpenCvSharp从摄像头获取图片的基本方式。 …...
【基础】【Python网络爬虫】【12.App抓包】reqable 安装与配置（附大量案例代码）（建议收藏）
Python网络爬虫基础 App抓包1. App爬虫原理2. reqable 的安装与配置reqable 安装教程reqable 的配置 3. 模拟器的安装与配置夜神模拟器的安装夜神模拟器的配置配置代理配置证书 4. 内联调试及注意事项软件启动顺开启抓包功reqable面板功列表部件功能列表数据快捷操作栏 夜神模拟…...
LabVIEW在电机噪声与振动探测的应用
LabVIEW在电机噪声与振动探测的应用 硬件部分是电机噪声和振动测试分析系统的基础，主要由三大核心组件构成：高灵敏度振动传感器、先进的信号调理电路和高性能数据采集卡。这些设备协同工作，确保了从电机捕获的噪声和振动信号的准确性和可靠性…...
编码器是什么，以光电编码器为例，说明一下光电编码器的名字由来，结构，原理，特点，用处
问题描述： 问题解答： 定义：编码器是一种测量角度、位置、速度等物理量的传感器，它可以将物理量转换成电信号，以便计算机或控制系统进行处理和控制。编码器通常由码盘和光电转换器组成，码盘上刻有若干条码道…...
MySQL：主从复制
准备两台服务器：安装好mysql mysql1：192.168.2.222 master mysql2：192.168.2.226 slave 1、主从服务器分别作以下 1.1、版本一致 1.2、初始化表，并在后台启动mysql 1.3、修改root的密码 2、修改主服务器master #vi /etc/my…...
【K8S 二进制部署】部署Kurbernetes的网络组件、高可用集群、相关工具
目录 一、K8S的网络类型： 1、K8S中的通信模式： 1.1、、pod内部之间容器与容器之间的通信 1.2、同一个node节点之内，不同pod之间的通信方式： 1.3、不同node节点上的pod之间是如何通信的呢？ 2、网络插件一ÿ…...
Ubuntu 常用命令之 locate 命令用法介绍
🔥Linux/Ubuntu 常用命令归类整理 locate命令是在Ubuntu系统下用于查找文件或目录的命令。它使用一个预先构建的数据库（通常由updatedb命令创建）来查找文件或目录，因此它的查找速度非常快。 plocate 安装 locate 不是 Ubuntu 系统的原生命令/功能，要想在 Ubuntu 系统中…...
java中file类常用方法举例说明
java中file类常用方法举例说明 当使用 java.io.File 类时，以下是一些常用方法的举例说明： 创建文件或目录： // 使用路径名创建File实例 File file new File("C:\\Users\\UserName\\Documents\\example.txt");// 使用父路径和子路…...
机器学习分类模型
机器学习常见分类模型及特点 机器学习常见分类模型优缺点 决策树模型 决策树（Decision Tree）是一类常见的机器学习方法，可应用于分类与回归任务，这里主要讨论分类决策树。决策树是基于树结构来进行决策的。下图是使用决策树来决定…...
LaTeX符号大全：打破排版的边界
LaTeX符号大全：打破排版的边界 大家好，我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编，也是冬天不穿秋裤，天冷也要风度的程序猿！今天，让我们一起探索一门极富表现力的排版艺术——LaTeX&…...
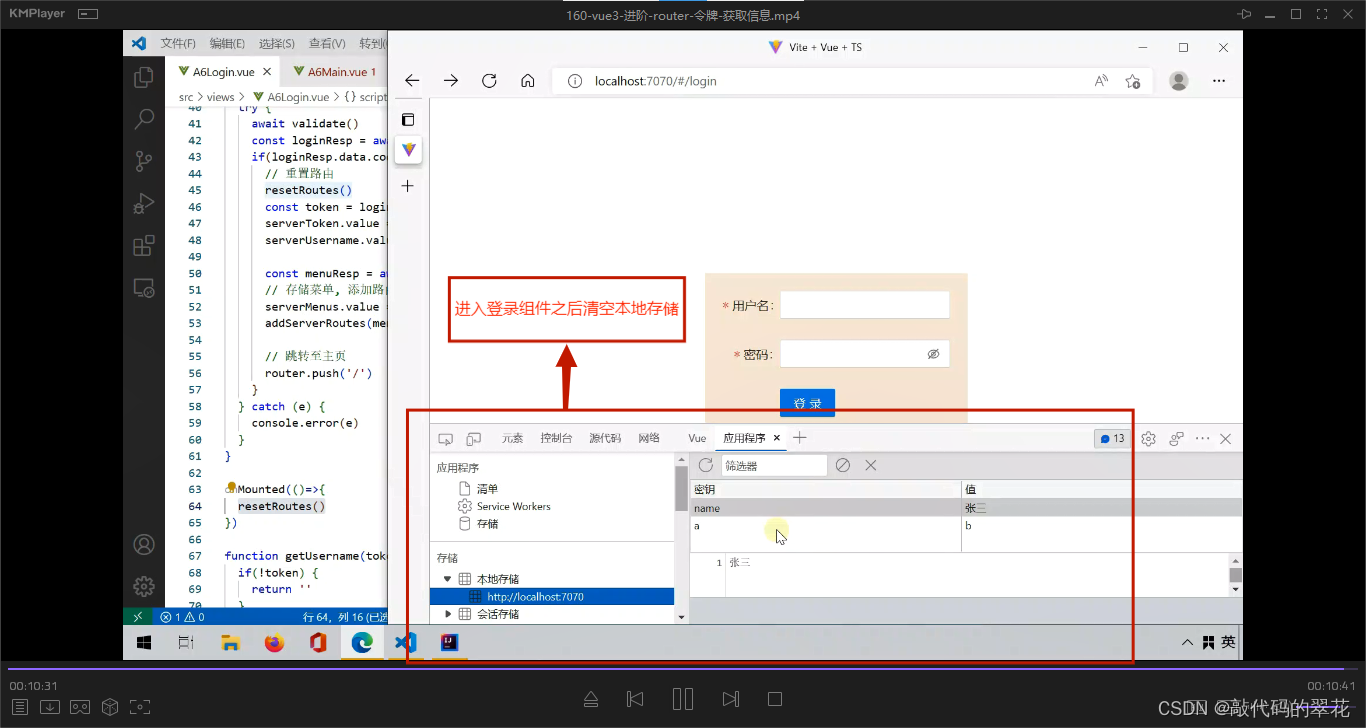
vue3-11
后端Java代码 src\router\a6router.ts文件 import { createRouter, createWebHashHistory } from vue-router import { useStorage } from vueuse/core import { Menu, Route } from ../model/Model8080 const clientRoutes [{path: /login,name: login,component: () > …...
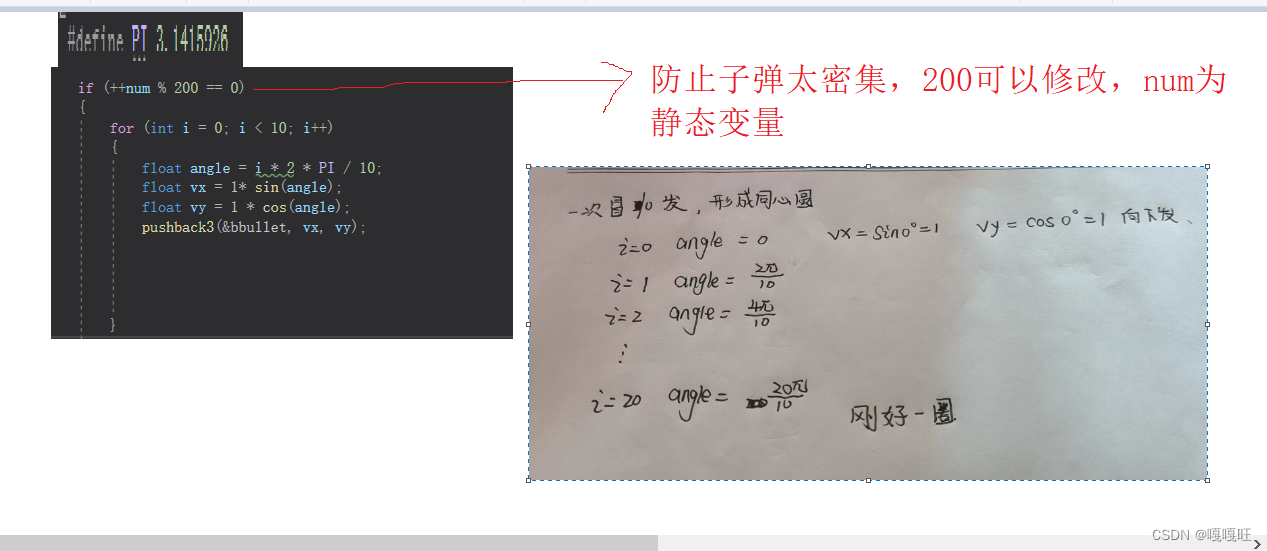
【c语言】飞机大战2
1.优化边界问题 之前视频中当使用drawAlpha函数时，是为了去除飞机后面变透明，当时当飞机到达边界的时候，会出现异常退出，这是因为drawAlpha函数不稳定，昨天试过制作掩码图，下载了一个ps,改的话，…...
Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码，写上注释 当然可以！这段代码是 Qt …...
CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本： 3.8.1 语言： JavaScript/TypeScript、C、Java 环境：Window 参考：Java原生反射机制 您好，我是鹤九日！ 回顾 在上篇文章中：CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
【决胜公务员考试】求职OMG——见面课测验1
2025最新版！！！6.8截至答题，大家注意呀！ 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:（ B ） A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
GO协程(Goroutine)问题总结
在使用Go语言来编写代码时，遇到的一些问题总结一下 [参考文档]：https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现： 今天在看到这个教程的时候，在自己的电…...
MySQL 主从同步异常处理
阅读原文：https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主，遇到的这个错误： Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一，通常表示ÿ…...
Java求职者面试指南：Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南：Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么？它的作用是什么？ Spring框架的核心容器是IoC（控制反转）容器。它的主要作用是管理对…...
QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下，音视频内容犹如璀璨繁星，点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频，到在线课堂中知识渊博的专家授课，再到影视平台上扣人心弦的高清大片，音…...
针对药品仓库的效期管理问题，如何利用WMS系统“破局”
案例： 某医药分销企业，主要经营各类药品的批发与零售。由于药品的特殊性，效期管理至关重要，但该企业一直面临效期问题的困扰。在未使用WMS系统之前，其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库，基于 mysql 库改进而来，具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点： 支持 Promise / async-await…...
链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好，我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题，统一使用 二重复合函数： z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式（偏导…...