图文证明 费马,罗尔,拉格朗日,柯西
图文证明 罗尔,拉格朗日,柯西
费马引理和罗尔都比较好证,不过多阐述,看图即可:
费马引理:
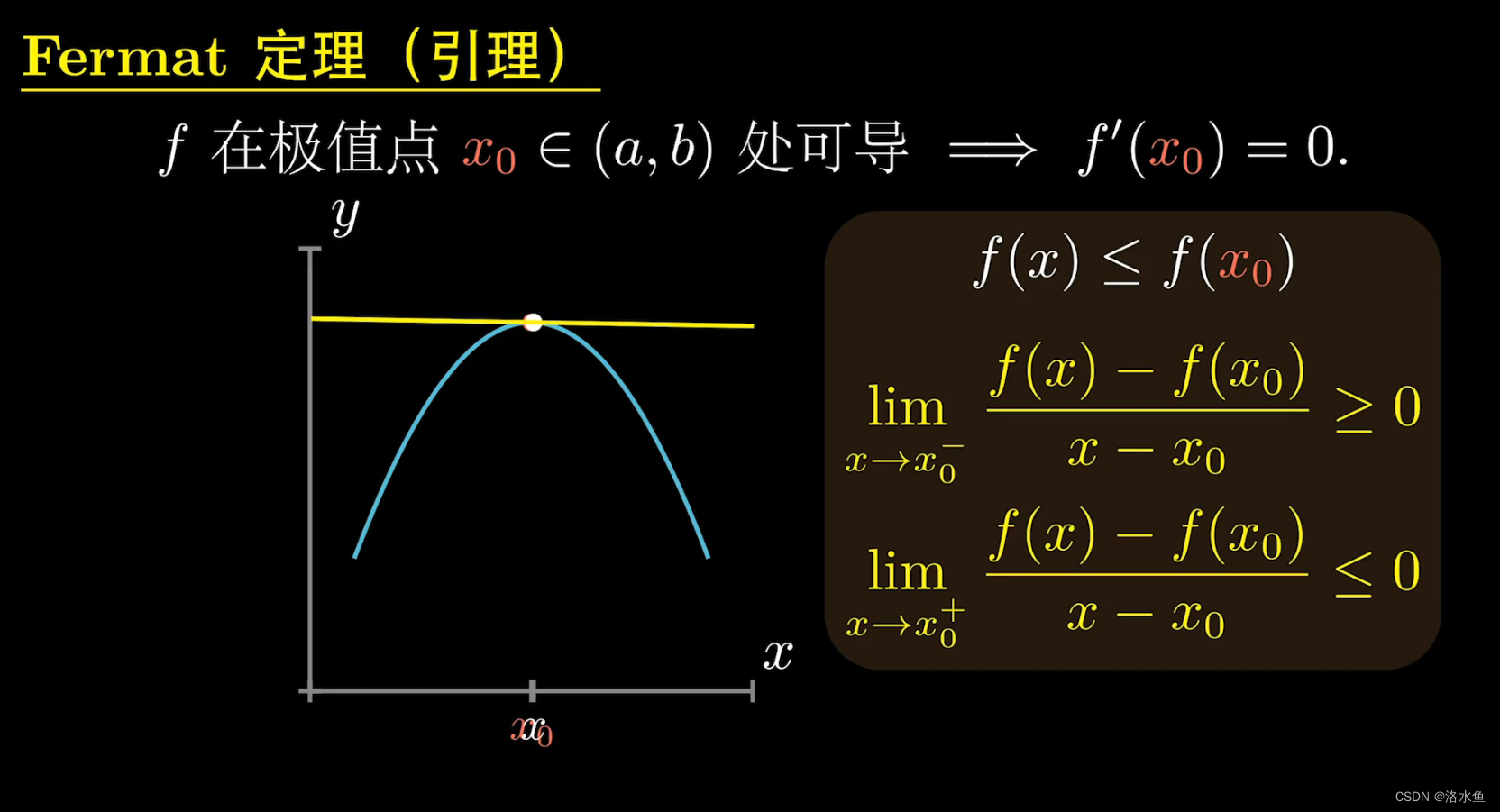
罗尔定理:

重点来证明拉格朗日和柯西
拉格朗日:

我认为不需要去看l(x)的那一行更好推:
详细的推理过程:
构造 h ( x ) = f ( x ) − l ( x ) , 因为 a , b 两点为交点 , f ( a ) = l ( a ) , f ( b ) = l ( b ) , 构造h(x) = f(x) - l(x), \quad \text{因为} \; a, b \; \text{两点为交点}, \; f(a) = l(a), \; f(b) = l(b), 构造h(x)=f(x)−l(x),因为a,b两点为交点,f(a)=l(a),f(b)=l(b),
所以 h ( a ) = h ( b ) = 0. 根据罗尔定理 , ∃ c ∈ ( a , b ) 使得 h ′ ( ξ ) = 0. \text{所以} \; h(a) = h(b) = 0. \quad \text{根据罗尔定理}, \; \exists \, c \in (a, b) \; \text{使得} \; h'(\xi ) = 0. 所以h(a)=h(b)=0.根据罗尔定理,∃c∈(a,b)使得h′(ξ)=0.
因为 h ( ξ ) = f ( ξ ) − l ( ξ ) , 我们有 h ′ ( ξ ) = f ′ ( ξ ) − l ′ ( ξ ) . 因此 , h ′ ( ξ ) = f ′ ( ξ ) − l ′ ( ξ ) = 0. \text{因为} \; h(\xi ) = f(\xi ) - l(\xi ), \; \text{我们有} \; h'(\xi ) = f'(\xi ) - l'(\xi ). \quad \text{因此}, \; h'(\xi ) = f'(\xi ) - l'(\xi ) = 0. 因为h(ξ)=f(ξ)−l(ξ),我们有h′(ξ)=f′(ξ)−l′(ξ).因此,h′(ξ)=f′(ξ)−l′(ξ)=0.
由此得出 f ′ ( ξ ) = l ′ ( ξ ) . \text{由此得出} \; f'(\xi ) = l'(\xi ). 由此得出f′(ξ)=l′(ξ).
根据两点式得: l ′ ( ξ ) = f ( b ) − f ( a ) b − a \text{根据两点式得:} \; l'(\xi ) = \frac{{f(b)-f(a)}}{{b-a}} 根据两点式得:l′(ξ)=b−af(b)−f(a)
由于已知 f ′ ( ξ ) = l ′ ( ξ ) , 你可以使用这个信息进一步推导出 f ′ ( x ) = l ′ ( x ) = f ( b ) − f ( a ) b − a . \text{由于已知} \; f'(\xi ) = l'(\xi ), \; \text{你可以使用这个信息进一步推导出} \; \ f'(x) = l'(x) = \frac{{f(b)-f(a)}}{{b-a}}. 由于已知f′(ξ)=l′(ξ),你可以使用这个信息进一步推导出 f′(x)=l′(x)=b−af(b)−f(a).
柯西:

给定两个函数 f ( x ) 和 g ( x ) \text{给定两个函数} \; f(x) \; \text{和} \; g(x) \; 给定两个函数f(x)和g(x)
在区间 [ a , b ] 上,其中 f ( x ) ≠ g ( x ) 。根据拉格朗日中值定理,存在 c ∈ ( a , b ) 使得 \text{在区间} \; [a, b] \; \text{上,其中} \; f(x) \neq g(x) \; \text{。根据拉格朗日中值定理,存在} \; c \in (a, b) \; \text{使得} 在区间[a,b]上,其中f(x)=g(x)。根据拉格朗日中值定理,存在c∈(a,b)使得
f ′ ( ξ ) = f ( b ) − f ( a ) b − a , g ′ ( ξ ) = g ( b ) − g ( a ) b − a . f'(\xi ) = \frac{f(b) - f(a)}{b - a}, \quad g'(\xi ) = \frac{g(b) - g(a)}{b - a}. f′(ξ)=b−af(b)−f(a),g′(ξ)=b−ag(b)−g(a).
现在,我们使用换元法,将 f ′ ( ξ ) 的 ( b − a ) 替换为 g ( b ) − g ( a ) g ′ ( ξ ) \text{现在,我们使用换元法,将} \; f'(\xi ) \; \text{的} \; (b - a) \; \text{替换为} \; \frac{g(b) - g(a)}{g'(\xi )} 现在,我们使用换元法,将f′(ξ)的(b−a)替换为g′(ξ)g(b)−g(a)
f ′ ( c ) = f ( b ) − f ( a ) g ( b ) − g ( a ) g ′ ( c ) . f'(c) = \frac{f(b) - f(a)}{\frac{g(b) - g(a)}{g'(c)}}. f′(c)=g′(c)g(b)−g(a)f(b)−f(a).
通过简化得到 f ′ ( c ) = f ( b ) − f ( a ) g ( b ) − g ( a ) ⋅ g ′ ( c ) . \text{通过简化得到} \; f'(c) = \frac{f(b) - f(a)}{g(b) - g(a)} \cdot g'(c). 通过简化得到f′(c)=g(b)−g(a)f(b)−f(a)⋅g′(c).
发现一个看一眼就明了的列子
拉格朗日:如果你一小时跑了5km,你的平均速度就是5km/h。那么在这一小时以内,要么一直保持5km/h,要么一部分比这个速度快,一部分比这个速度慢。在快慢转换的点,你的速度就是5km/h。
柯西:我一小时跑了5km,你一小时跑了20km。要么你的速度一直是我的20/5=4倍,要么你一部分比我四倍还快,一部分比我四倍慢,在这转换的这一点,你的速度是我的四倍。
参考视频:
罗尔、拉格朗日、柯西【中值定理】 证明
相关文章:

图文证明 费马,罗尔,拉格朗日,柯西
图文证明 罗尔,拉格朗日,柯西 费马引理和罗尔都比较好证,不过多阐述,看图即可: 费马引理: 罗尔定理: 重点来证明拉格朗日和柯西 拉格朗日: 我认为不需要去看l(x)的那一行更好推: 详细的推理过程: 构造 h ( x ) f ( x ) − l ( x ) , 因为 a , b 两点为交点 , f ( a ) l ( …...
CEC2017(Python):粒子群优化算法PSO求解CEC2017(提供Python代码)
一、CEC2017简介 参考文献: [1]Awad, N. H., Ali, M. Z., Liang, J. J., Qu, B. Y., & Suganthan, P. N. (2016). “Problem definitions and evaluation criteria for the CEC2017 special session and competition on single objective real-parameter numer…...
(一))
AUTOSAR从入门到精通- 虚拟功能总线(RTE)(一)
目录 前言 几个高频面试题目 RTE S/R接口implicit与Explicit的实现与区别 接口的代码 implicit...

B/S架构云端SaaS服务的医院云HIS系统源码,自主研发,支持电子病历4级
医院云HIS系统源码,自主研发,自主版权,电子病历病历4级 系统概述: 一款满足基层医院各类业务需要的云HIS系统。该系统能帮助基层医院完成日常各类业务,提供病患挂号支持、病患问诊、电子病历、开药发药、会员管理、统…...
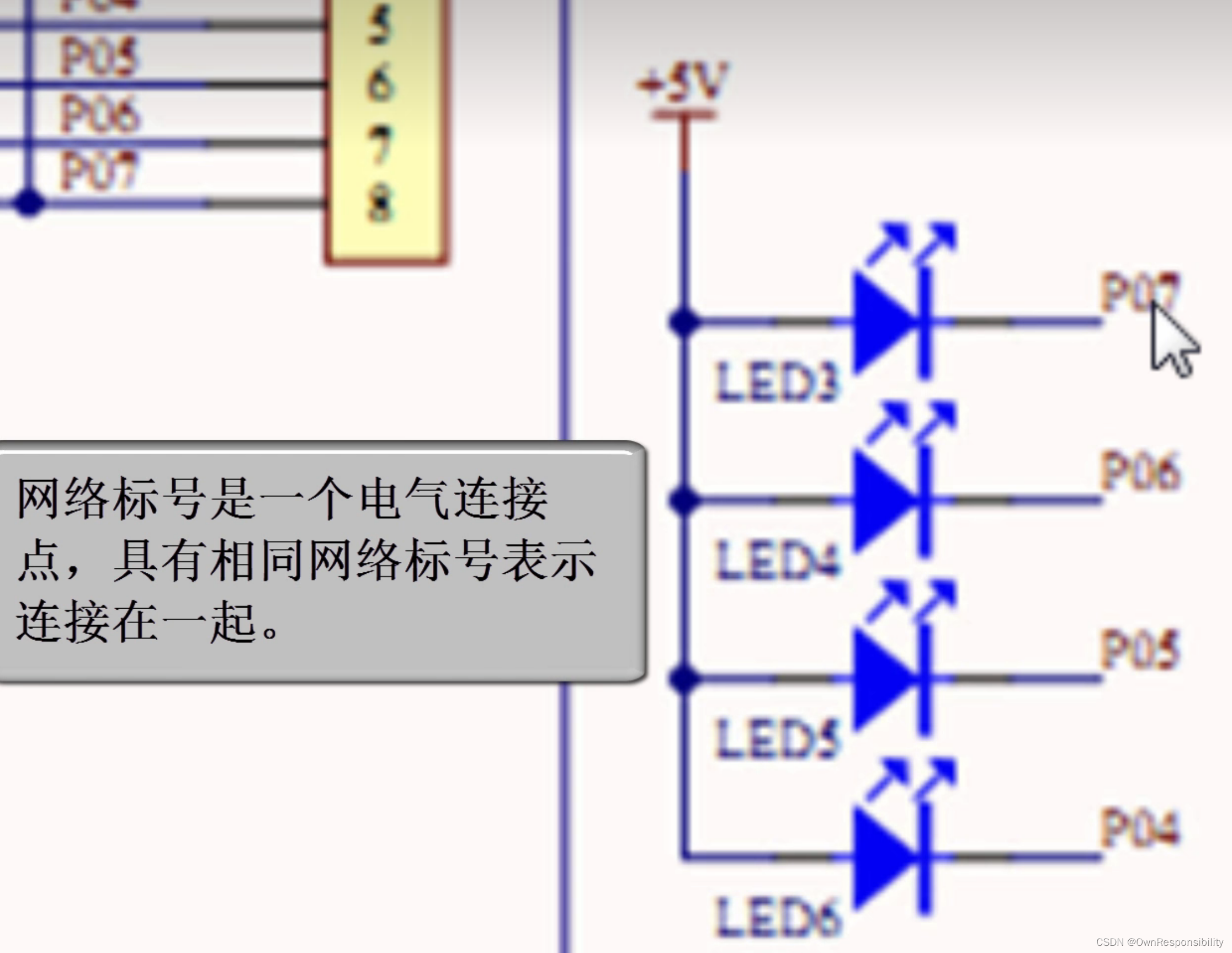
看懂基本的电路原理图(入门)
文章目录 前言一、二极管二、电容三、接地一般符号四、晶体振荡器五、各种符号的含义六、查看原理图的顺序总结 前言 电子入门,怎么看原理图,各个图标都代表什么含义,今天好好来汇总一下。 就比如这个电路原理图来说,各个符号都…...

赫夫曼树基本数据结构
自编头文件: #ifndef HUFFMAN_H_INCLUDED #define HUFFMAN_H_INCLUDED#include<limits.h> #include<string.h> typedef struct {unsigned int weight;unsigned int parent,lchild,rchild; }HTNode,*HuffmanTree; typedef char** HuffmanCode;void Sele…...
10TB海量JSON数据从OSS迁移至MaxCompute
前提条件 开通MaxCompute。 在DataWorks上完成创建业务流程,本例使用DataWorks简单模式。详情请参见创建业务流程。 将JSON文件重命名为后缀为.txt的文件,并上传至OSS。本文中OSS Bucket地域为华东2(上海)。示例文件如下。 {&qu…...
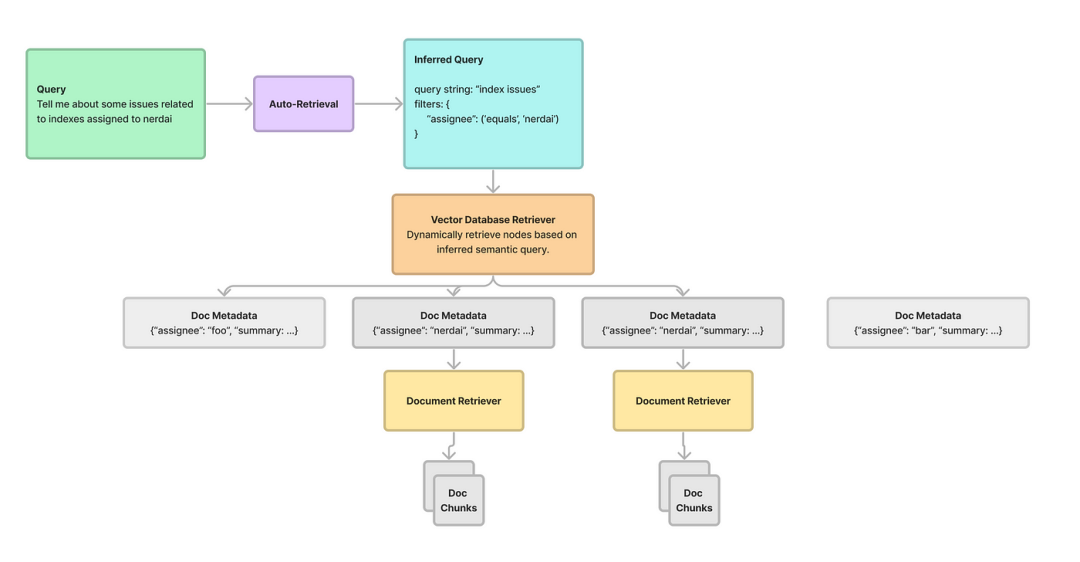
LLM之RAG实战(九)| 高级RAG 03:多文档RAG体系结构
在RAG(检索和生成)这样的框架内管理和处理多个文档有很大的挑战。关键不仅在于提取相关内容,还在于选择包含用户查询所寻求的信息的适当文档。基于用户查询对齐的多粒度特性,需要动态选择文档,本文将介绍结构化层次检索…...

Windows电脑引导损坏?按照这个教程能修复
前言 Windows系统的引导一般情况下是不会坏的,小伙伴们可以不用担心。发布这个帖子是因为要给接下来的文章做点铺垫。 关注小白很久的小伙伴应该都知道,小白的文章都讲得比较细。而且文章与文章之间的关联度其实还是蛮高的。在文章中,你会遇…...

记Android字符串资源支持的参数类型
参数以%开头,后拼接对应的参数类型名称,如下所示: <string name"tips">Hello, %s! You have some new messages.</string> 类型名称如下所示: s字符串格式用于插入字符串值。例如,"Hel…...
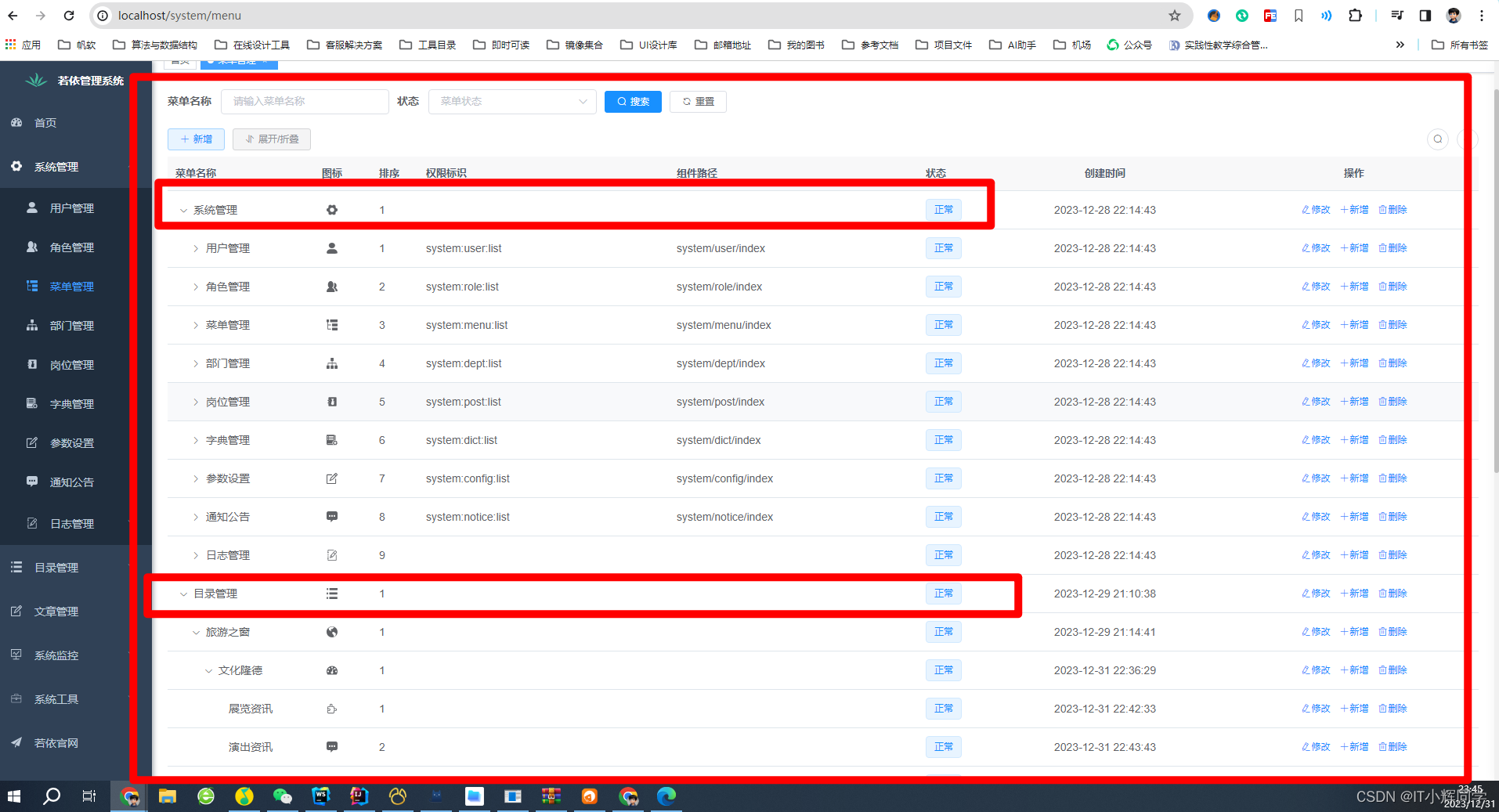
Java实现树结构(为前端实现级联菜单或者是下拉菜单接口)
Java实现树结构(为前端实现级联菜单或者是下拉菜单接口) 我们常常会遇到这样一个问题,就是前端要实现的样式是一个级联菜单或者是下拉树,如图 这样的数据接口是怎么实现的呢,是什么样子的呢? 我们可以看看 …...

MySQL中常用的数据类型
整型 int 有符号范围: -2147483648 ~ 2147483647 int unsigned 无符号范围: 0 ~ 4294967295 int(5) zerofill 仅用于显示,当不满足5位时,按照左边补0,例如: 00002满足时,正常显示 tinyint[(m)] [unsigned] [zerofill] 有符号&a…...

HTML+CSS+JS制作三款雪花酷炫特效
🎀效果展示 🎀代码展示 <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html...
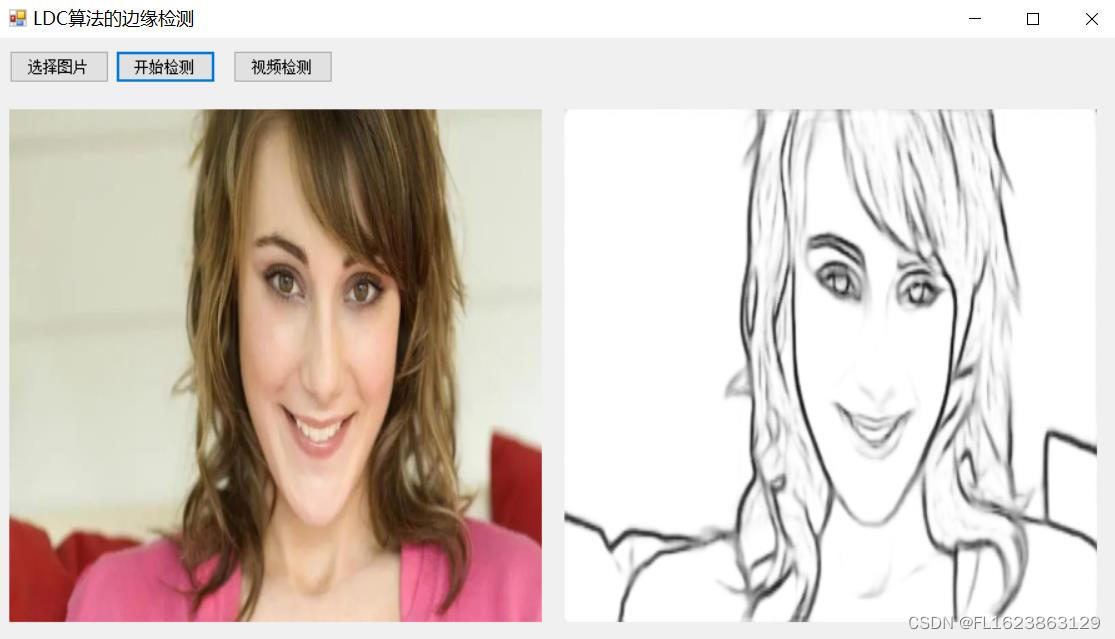
[C#]使用ONNXRuntime部署一种用于边缘检测的轻量级密集卷积神经网络LDC
源码地址: github.com/xavysp/LDC LDC: Lightweight Dense CNN for Edge Detection算法介绍: 由于深度学习方法的快速发展,近年来,用于执行图像边缘检测的卷积神经网络(CNN)模型爆炸性地传播。但边缘检测…...

ZigBee案例笔记 - 无线点灯
文章目录 无线点灯实验概述工程关键字工程文件夹介绍Basic RF软件设计框图简单说明工程操作Basic RF启动流程Basic RF发送流程Basic RF接收流程 无线点灯案例无线点灯现象 无线点灯实验概述 ZigBee无线点灯实验(即Basic RF工程),由TI公司提供…...
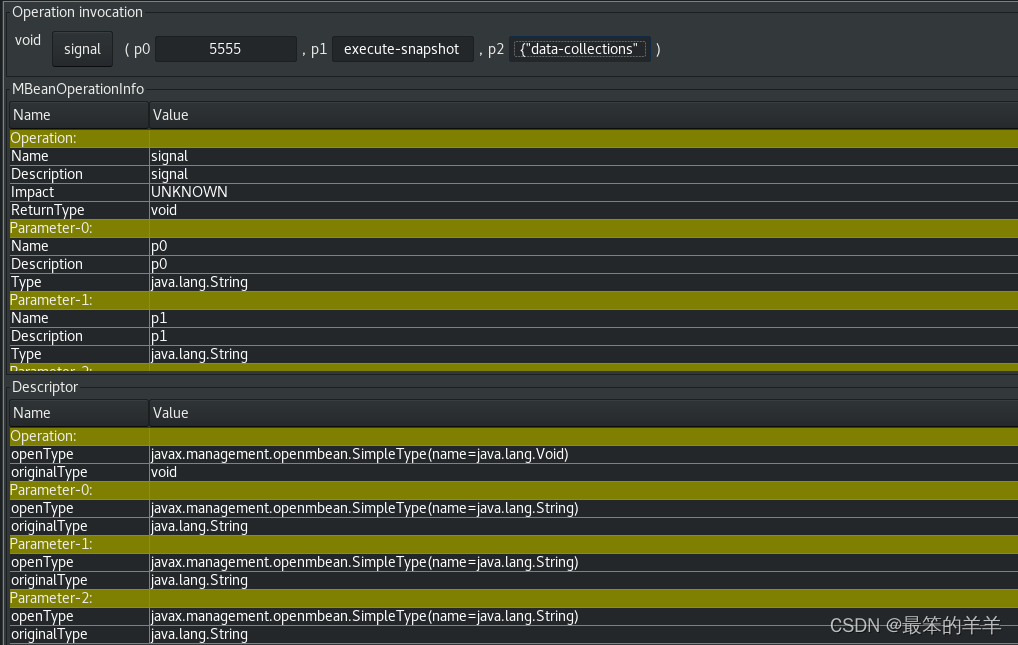
Debezium日常分享系列之:向 Debezium 连接器发送信号
Debezium日常分享系列之:向 Debezium 连接器发送信号 一、概述二、激活源信号通道三、信令数据集合的结构四、创建信令数据集合五、激活kafka信号通道六、数据格式七、激活JMX信号通道八、自定义信令通道九、Debezium 核心模块依赖项十、部署自定义信令通道十一、信…...

《C#程序设计教程》总复习
一、单项选择题 1.short 类型的变量在内存中占据的位数是 ( )。 A. 8 B. 16 C. 32 D. 64 2.对千 int[ 4,5]型的数组 a, 数组元素 a[2,3] 存在数组第 ( )个位置上。 A. 11 B. 12 C. 14 D. 15 3.设 int 类型变量 x,y,z 的值分别是2、3、6 , 那么…...

为什么ChatGPT选择了SSE,而不是WebSocket?
我在探索ChatGPT的使用过程中,发现了一个有趣的现象:ChatGPT在实现流式返回的时候,选择了SSE(Server-Sent Events),而非WebSocket。 那么问题来了:为什么ChatGPT选择了SSE,而不是We…...
appium入门基础
介绍 appium支持在不同平台的UI自动化,如web,移动端,桌面端等。还支持使用java,python,js等语言编写自动化代码。主要用于自动化测试脚本,省去重复的手动操作。 Appium官网 安装 首先必须环境有Node.js用于安装Appium。 总体来…...
jsp介绍
JSP 一种编写动态网页的语言,可以嵌入java代码和html代码,其底层本质上为servlet,html部分为输出流,编译为java文件 例如 源jsp文件 <% page contentType"text/html; charsetutf-8" language"java" pageEncoding&…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
