DFS算法查找所有路径详解
DFS算法查找所有路径详解
算法介绍
深度优先搜索(Depth-First Search,DFS)是一种图遍历算法,它从起始节点开始,沿着一条路径尽可能深入,直到达到最深的节点,然后回溯到前一节点,继续探索下一条路径。DFS通常使用递归或栈(非递归)来实现。
以下是DFS算法的基本步骤:
- 选择起始节点: 从图中选择一个起始节点作为当前节点;
- 标记节点: 标记当前节点为已访问,以防止重复访问;
- 探索邻居节点: 对于当前节点的未访问邻居节点,选择一个邻居节点作为新的当前节点,然后重复步骤2和步骤3;
- 回溯: 如果当前节点没有未访问的邻居节点,回溯到上一节点,重复步骤3;
- 重复过程: 重复步骤3和步骤4,直到所有节点都被访问。
递归实现的伪代码
function DFS(node):if node is not visited:mark node as visitedfor each neighbor of node:DFS(neighbor)非递归实现的伪代码
DFS的非递归实现通常使用栈来模拟递归调用的过程,具体步骤如下:
- 创建一个空栈,并将起始节点压入栈中;
- 进入循环,直到栈为空;
- 弹出栈顶节点作为当前节点;
- 如果当前节点未访问,标记为已访问;
- 遍历当前节点的邻居节点,将未访问的邻居节点压入栈中;
- 重复步骤3到步骤5,直到栈为空为止。
注意:在处理连通图时可能导致栈溢出,因此在实际应用中可能需要注意栈深度的问题。
伪代码如下:
function DFS_non_recursive(start):stack = empty stackpush start onto stackwhile stack is not empty:current = pop from stackif current is not visited:mark current as visitedfor each neighbor of current:push neighbor onto stack具体算法实现
由于可能存在非常多的路径,我们设置一个maxLength,表示限制经过的节点个数。
void Graph::DFS(int current, int end, std::unordered_set<int>& visited, std::vector<int>& path, int maxLength)
{static int currentLength = 0;static int i = 1;visited.insert(current);path.push_back(current);if (path.size() <= maxLength) {if (current == end){// 生成路径for (int node : path) {std::cout<<node<<' ';}std::cout<<"路径总长度为:"<<currentLength<<std::endl;}else{for (int neighbor = 0; neighbor < V; ++neighbor){if (adjMatrix[current][neighbor] != INF && visited.find(neighbor) == visited.end()) {int edgeWeight = adjMatrixLength[current][neighbor];currentLength += edgeWeight;DFS(neighbor, end, visited, path, maxLength);currentLength -= edgeWeight; // 回溯时减去当前边的长度}}}}visited.erase(current);path.pop_back();
}
相关文章:

DFS算法查找所有路径详解
DFS算法查找所有路径详解 算法介绍 深度优先搜索(Depth-First Search,DFS)是一种图遍历算法,它从起始节点开始,沿着一条路径尽可能深入,直到达到最深的节点,然后回溯到前一节点,继…...
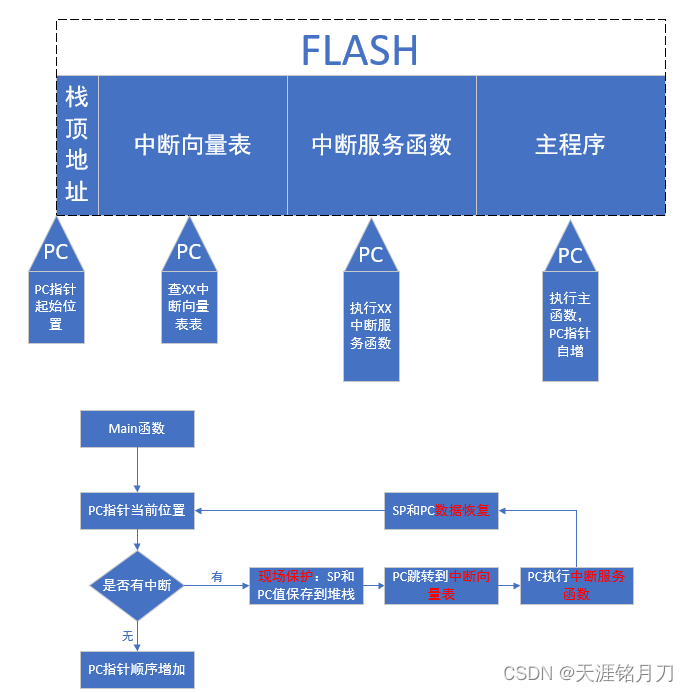
单片机的存储、堆栈与程序执行方式
一、单片机存储区域 如图所示位STM32F103ZET6的参数: 单片机的ROM(内部FLASH):512KB,用来存放程序代码的空间。 单片机的RAM:64KB,一般都被分配为堆、栈、变量等的空间。 二、堆和栈的概念 …...

Web3开发成本和主要特性
多年来,技术不断进步,可帮助您的业务领先于竞争对手。如今,您可以看到许多更新和变化,使技术更加先进,对企业更加有用。到现在为止,web1.2和2.0比较流行,但是要知道web 3才是技术之父࿰…...

【数学建模美赛M奖速成系列】Matplotlib绘图技巧(一)
Matplotlib图像基础 写在前面1 基本绘图实例:sin、cos函数图2 plot()函数详解**kwargs参数: 3 matplotlib中绘图的默认配置4 设置图的横纵坐标的上下界5 设置横纵坐标上的记号6 调整图像的脊柱7 添加图例8 给一些特殊点加注释9 子图最后 写在前面 前面我…...
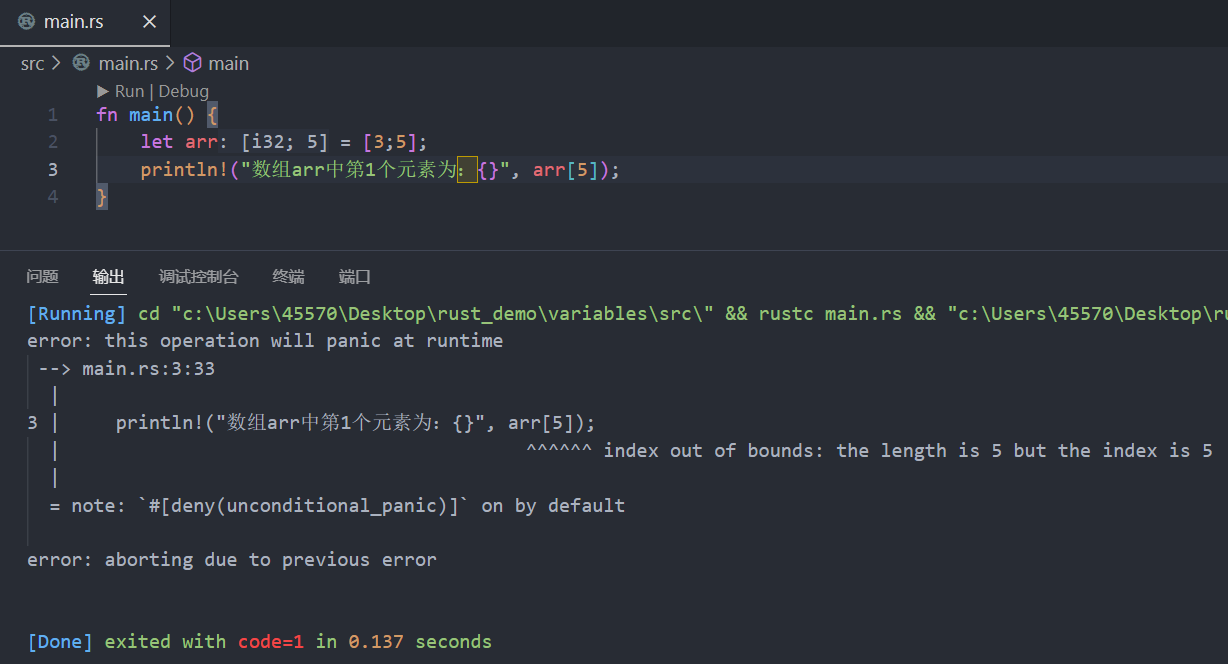
005、数据类型
1. 关于数据类型 Rust中,每个值都有其特定的数据类型,Rust会根据数据的类型来决定如何处理它们。 Rust是一门静态类型语言,它在编译程序的过程中就需要知道所有变量的具体类型。在大部分情况下,编译器可以根据我们如何绑定、使用变…...
)
软考网络工程师考试大纲(2018年最新版)
本书是全国计算机专业技术资格考试办公室组织编写的网络工程师考试大纲,本书除大纲内容外,还包括了人力资源和社会保障部、工业和信息化部的有关文件以及考试简介。 网络工程师考试大纲是针对本考试的计算机网络中级资格制定的。通过本考试的考生,可被用人单位择优聘任为工…...

【数据结构】栈【详解】
目录 栈的定义: 栈的声明与定义: 头文件的包含: 对栈的基本操作: 栈的初始化: 摧毁栈: 入栈: 编辑 出栈: 编辑 输出栈顶位置: 输出栈的当前大小: 判空操…...

CSS 纵向底部往上动画
<template><div class"container" mouseenter"startAnimation" mouseleave"stopAnimation"><!-- 旋方块 --><div class"box" :class"{ scale-up-ver-bottom: isAnimating }"><!-- 元素内容 --&g…...
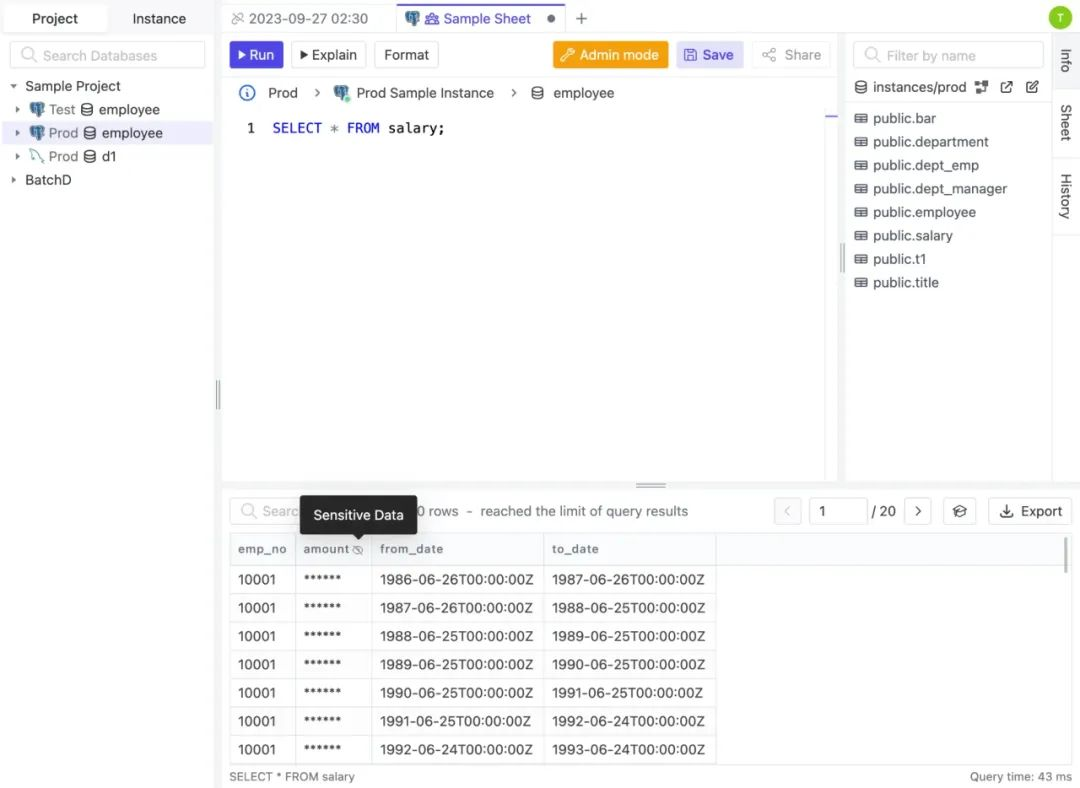
常用的 MySQL 可视化客户端
数据库可视化客户端(GUI)让用户在和数据库进行交互时,能直观地查看、创建和修改对象,如:表、行和列。让数据库操作变得更方便了。 今天,我们来了解下目前市场上最常用的 MySQL 可视化客户端。 官方&#x…...

C#使用SyntaxTree获取.cs文件中的属性名和注释
有时候,我们可能需要获取.cs文件中的属性和对应的注释来生成一些代码,比如SQL查询什么的。 但使用正则匹配有时候会不准确。搜索了下,发现微软提供了代码解析的API。 具体如下两个方法: /// <summary> /// 获取所有属性和…...
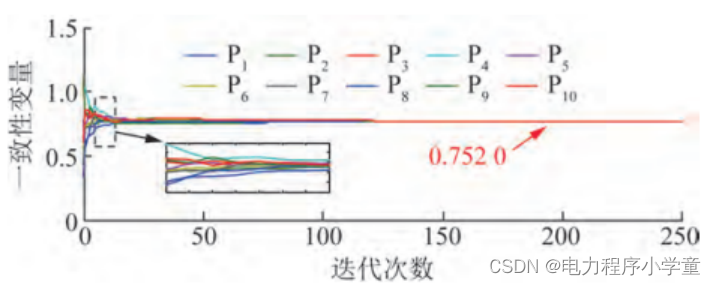
基于价值认同的需求侧电能共享分布式交易策略(matlab完全复现)
目录 1 主要内容 2 部分程序 3 程序结果 4 下载链接 1 主要内容 该程序完全复现《基于价值认同的需求侧电能共享分布式交易策略》,针对电能共享市场的交易机制进行研究,提出了基于价值认同的需求侧电能共享分布式交易策略,旨在降低电力市…...
门控循环单元(GRU)-多输入回归预测
目录 一、程序及算法内容介绍: 基本内容: 亮点与优势: 二、实际运行效果: 三、部分程序: 四、全部代码数据分享: 一、程序及算法内容介绍: 基本内容: 本代码基于Matlab平台编译…...
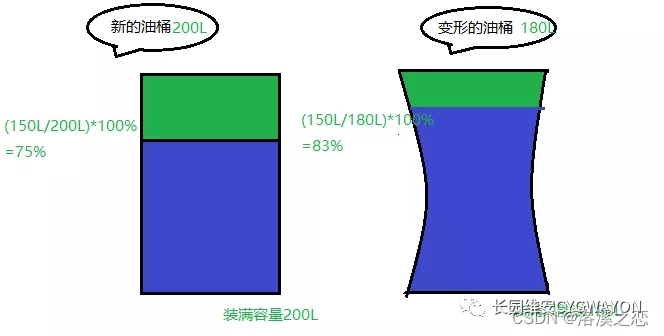
电池管理系统BMS中SOC算法通俗解析(二)
下面简单介绍下我们BMS保护板使用的SOC估算方法。我们算法的主要是针对电流积分法计算SOC的局限性进行改进: ●电池包第一次上电使用开路电压法估算SOC。第一次上电,根据电池包厂家给出的电压和剩余容量二维关系图大概估算出目前电池包的剩余容量即SOC。…...

YOLOv5改进 | 2023主干篇 | 华为最新VanillaNet主干替换Backbone实现大幅度长点
一、本文介绍 本文给大家来的改进机制是华为最新VanillaNet网络,其是今年最新推出的主干网络,VanillaNet是一种注重极简主义和效率的神经网络架构。它的设计简单,层数较少,避免了像深度架构和自注意力这样的复杂操作(需要注意的是…...
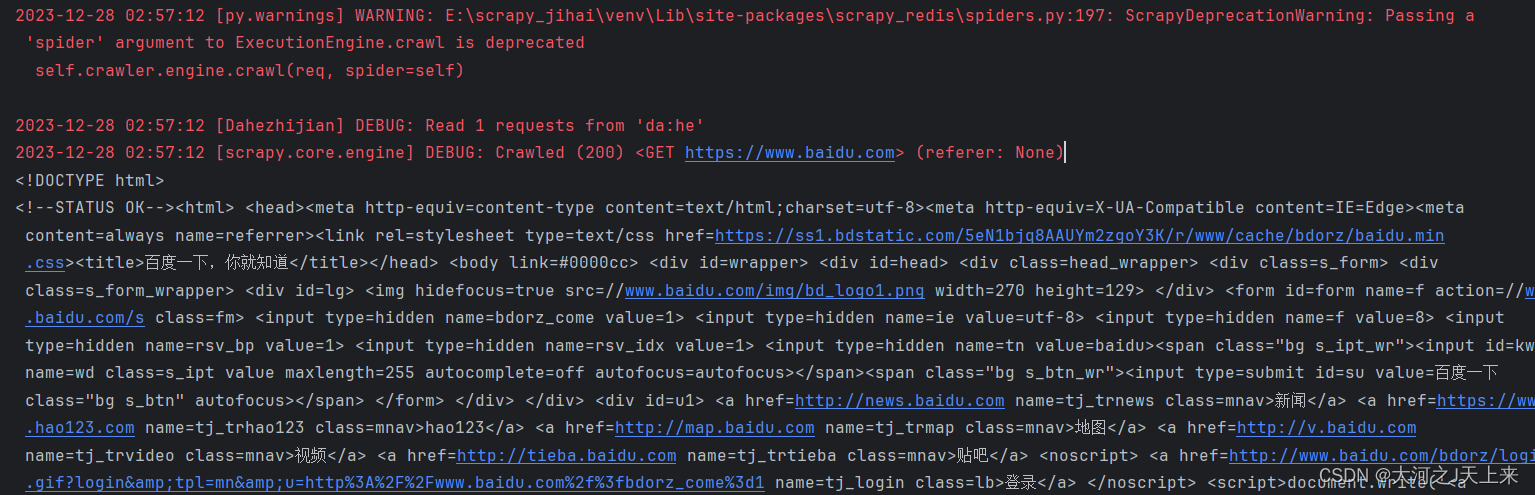
爬虫工作量由小到大的思维转变---<第三十三章 Scrapy Redis 23年8月5日后会遇到的bug)>
前言: 收到回复评论说,按照我之前文章写的: 爬虫工作量由小到大的思维转变---<第三十一章 Scrapy Redis 初启动/conn说明书)>-CSDN博客 在启动scrapy-redis后,往redis丢入url网址的时候遇到: TypeError: ExecutionEngine.crawl() got an unexpected …...

PostgreSQL | 概念 | 什么是OLTPOLAP?
什么是OLTP&OLAP? 大白话理解:业务系统都可以称作OLTP,基于业务系统产生的数据进行数据分析和决策的都可以称为OLAP。 OLTP OLTP( Online Transaction Processing)在线事务处理系统 用途: 用于支持日…...
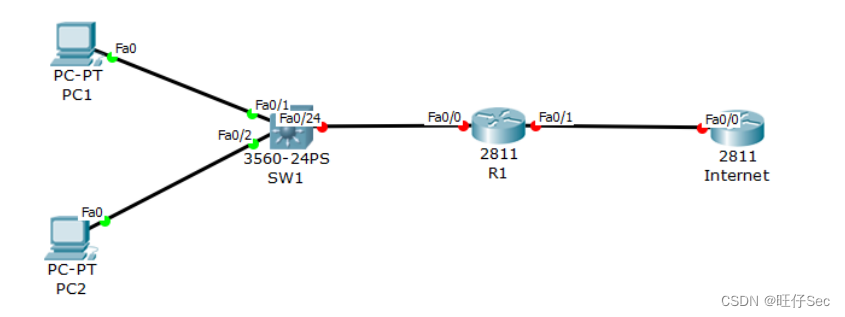
2023年成都市中等职业学校学生技能大赛“网络搭建及应用”赛项竞赛样卷
2023年成都市中等职业学校学生技能大赛 “网络搭建及应用”赛项竞赛样卷 (总分1000分) 目录 2023年成都市中等职业学校学生技能大赛 “网络搭建及应用”赛项竞赛样卷 网络建设与调试项目(500分) 服务器搭建与运维项目(…...

Angular进阶之六:Progressive rendering
简介 Progressive Rendering 是一种提高 Web 应用性能的方法,允许页面在加载过程中逐步呈现,以提高用户体验。在本文中,我们将探讨如何在 Angular 中通过自定义指令实现 Progressive Rendering,特别是处理从服务器获取大量数据的…...

机器人中的数值优化之线性共轭梯度法
欢迎大家关注我的B站: 偷吃薯片的Zheng同学的个人空间-偷吃薯片的Zheng同学个人主页-哔哩哔哩视频 (bilibili.com) 本文ppt来自深蓝学院《机器人中的数值优化》 目录 1.无约束优化方法对比 2.Hessian-vec product 3.线性共轭梯度方法的步长编辑 4.共轭梯度…...

嵌入式Linux C语言介绍
目录 一.前言 二.C语言的特点 一.前言 开发工具通常依赖于操作系统提供的各种功能和服务。许多开发工具都基于操作系统的API(应用程序接口)进行开发,这些API提供了文件处理、网络通信、图形界面等核心功能。没有操作系统的支持,…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
