力扣labuladong一刷day49天迪杰斯特拉
力扣labuladong一刷day49天迪杰斯特拉
文章目录
- 力扣labuladong一刷day49天迪杰斯特拉
- 一、743. 网络延迟时间
- 二、1631. 最小体力消耗路径
- 三、1514. 概率最大的路径
一、743. 网络延迟时间
题目链接:https://leetcode.cn/problems/network-delay-time/
使用迪杰斯特拉解决加权图某点到所有节点距离的问题。
如果是无权图,采用广度优先遍历即可,就把图想象成一颗树,广度优先就可以说是层序遍历。
而加权图寻找最短距离,最经典算法就是迪杰斯特拉算法,我们可以计算出某一个点到任意一个之间的最短距离。我们采用优先级队列,里面的每一个元素记录的是某点到起点之间的最短距离,我们会一直按照最短距离更新,这样到达结尾后即可得到最短距离。
class Solution {public int networkDelayTime(int[][] times, int n, int k) {List<int[]>[] graph = new ArrayList[n + 1];for (int i = 0; i <= n; i++) {graph[i] = new ArrayList<>();}for (int[] time : times) {int a = time[0], b = time[1], c = time[2];graph[a].add(new int[]{b, c});}int[] dist = djk(k, graph);int res = -1;for (int i = 1; i < dist.length; i++) {if (dist[i] == Integer.MAX_VALUE) return -1;res = Math.max(res, dist[i]);}return res;}class State {int id;int sToMe;public State(int id, int sToMe) {this.id = id;this.sToMe = sToMe;}}int[] djk(int start, List<int[]>[] graph) {int[] dist = new int[graph.length];Arrays.fill(dist, Integer.MAX_VALUE);PriorityQueue<State> pq = new PriorityQueue<>((a, b) -> a.sToMe - b.sToMe);dist[start] = 0;pq.add(new State(start, 0));while (!pq.isEmpty()) {State poll = pq.poll();int id = poll.id;int cur = poll.sToMe;if (cur > dist[id]) continue;for (int[] ints : graph[id]) {int nextId = ints[0];int temp = dist[id] + ints[1];if (temp < dist[nextId]) {dist[nextId] = temp;pq.add(new State(nextId, temp));}}}return dist;}
}
二、1631. 最小体力消耗路径
题目链接:https://leetcode.cn/problems/path-with-minimum-effort/
思路:基本上就是迪杰斯特拉的典型题目,只不过这一次求的是最小消耗,但我们在过程中需要求每一条路径的最大消耗,在去往下一个点时选择这些最大消耗中的最小消耗,做为路径的延伸。
class Solution {public int minimumEffortPath(int[][] heights) {int r = heights.length, c = heights[0].length;return djk(heights);}List<int[]> getList(int x, int y, int r, int c) {int[][] temp = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};List<int[]> list = new ArrayList<>();for (int[] ints : temp) {int nx = x + ints[0], ny = y + ints[1];if (nx < 0 || nx >= r || ny < 0 || ny >= c) continue;list.add(new int[] {nx, ny});}return list;}class State {int x;int y;int sToMe;public State(int x, int y, int sToMe) {this.x = x;this.y = y;this.sToMe = sToMe;}}int djk(int[][] heights) {int r = heights.length, c = heights[0].length;int[][] dist = new int[r][c];PriorityQueue<State> pq = new PriorityQueue<>((a, b)-> a.sToMe - b.sToMe);for (int i = 0; i < r; i++) {Arrays.fill(dist[i], Integer.MAX_VALUE);}pq.add(new State(0, 0, 0));dist[0][0] = 0;while (!pq.isEmpty()) {State poll = pq.poll();int x = poll.x, y = poll.y;int cur = poll.sToMe;if (x == r-1 && y == c-1) return cur;if (cur > dist[x][y]) continue;for (int[] ints : getList(x, y, r, c)) {int nLen = Math.max(dist[x][y], Math.abs(heights[x][y]-heights[ints[0]][ints[1]]));if (nLen < dist[ints[0]][ints[1]]) {dist[ints[0]][ints[1]] = nLen;pq.add(new State(ints[0], ints[1], nLen));}}}return -1;}
}
三、1514. 概率最大的路径
题目链接:https://leetcode.cn/problems/path-with-maximum-probability/
思路:这题和上一题又有点不一样,相当于求最长路径,那么需要把优先级队列按照从大到小排序即可。
class Solution {public double maxProbability(int n, int[][] edges, double[] succProb, int start_node, int end_node) {List<double[]>[] graph = new ArrayList[n];for (int i = 0; i < n; i++) {graph[i] = new ArrayList<>();}for (int i = 0; i < edges.length; i++) {int from = edges[i][0], to = edges[i][1];graph[from].add(new double[]{to, succProb[i]});graph[to].add(new double[]{from, succProb[i]});}return djk(graph, start_node, end_node);}class State{int id;double sToE;public State(int id, double sToE) {this.id = id;this.sToE = sToE;}}double djk(List<double[]>[] graph, int s, int e) {double[] dist = new double[graph.length];PriorityQueue<State> pq = new PriorityQueue<>((a, b)->Double.compare(b.sToE, a.sToE));Arrays.fill(dist, -1);dist[s] = 1;pq.add(new State(s, 1));while (!pq.isEmpty()) {State poll = pq.poll();int id = poll.id;double cur = poll.sToE;if (id == e) return cur;if (cur < dist[id]) continue;for (double[] ints : graph[id]) {int to = (int) ints[0];double nLen = cur * ints[1];if (nLen > dist[to]) {dist[to] = nLen;pq.add(new State(to, nLen));}}}return 0.0;}
}
相关文章:

力扣labuladong一刷day49天迪杰斯特拉
力扣labuladong一刷day49天迪杰斯特拉 文章目录 力扣labuladong一刷day49天迪杰斯特拉一、743. 网络延迟时间二、1631. 最小体力消耗路径三、1514. 概率最大的路径 一、743. 网络延迟时间 题目链接:https://leetcode.cn/problems/network-delay-time/ 使用迪杰斯特…...
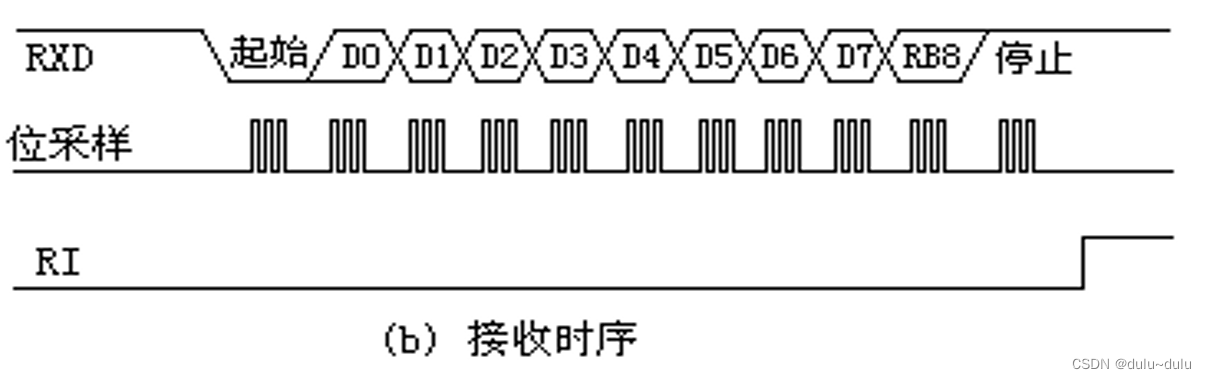
MCS接口技术----定时/计数,中断
目录 一.中断系统相关寄存器 1.51单片机中断系统的总体结构: 2.中断源的中断级别(由高到低): 3.与中断有关的四个寄存器: (1)TCON---定时控制寄存器 (2)IE---中断允…...

Java开发框架和中间件面试题(10)
目录 104.怎么保证缓存和数据库数据的一致性? 105.什么是缓存穿透,什么是缓存雪崩?怎么解决? 106.如何对数据库进行优化? 107.使用索引时有哪些原则? 108.存储过程如何进行优化? 109.说说…...

C++ 具名要求-基本概念-指定该类型对象可以从右值构造
指定该类型对象可以从右值构造 指定该类型的实例可以从一个右值实参构造。 要求 以下情况下,类型 T 满足可移动构造 (MoveConstructible) : 给定 T 类型的右值表达式 rv任意标识符 u 下列表达式必须合法且拥有其指定的效果 表达式后条件T u rv;u…...

Python如何把类当做字典来访问及浅谈Python类命名空间
Python如何把类当做字典来访问 Python把类当做字典来访问 定义一个类将它实例化,我们可以通过obj.属性来访问类的属性,如果想获取类的所有实例变量,我们可以使用obj.__dict__来访问,如下: class A:def __init__(self)…...

简述Redis备份策略以及对应的实现机制
引言 Redis作为高性能的内存数据库,数据的安全性至关重要。一旦数据丢失,可能会对业务造成重大影响。因此,备份Redis数据是每个Redis使用者都必须考虑的问题。本文将介绍Redis的备份策略以及对应的实现机制。 一、备份策略 1.1 定期备份 …...

【5G PHY】5G 物理层加速卡介绍
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

lftp学习笔记
目录 0. ftp vs. lftp1. 安装2. 常用命令2.1 登录2.2 文件管理2.3 文件传输 3. 脚本编程4. 实践中的问题排查参考 0. ftp vs. lftp lftp是一款文件传输工具,支持FTP、HTTP、SFTP、FISH等多种协议。 功能ftplftp数据传输文件文件、文件夹多线程传输支持断点续传支持…...
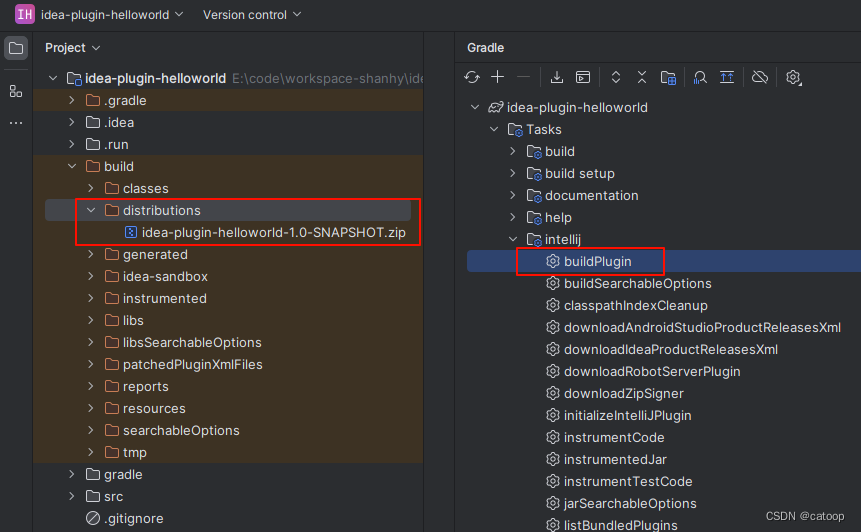
idea 插件开发之 HelloWorld
前言 本文使用的 idea 2023.3 版本进行插件入门开发,首先要说明的是 idea 2023 版本及以后的 idea,对插件开发进行了一定程度的变动: 1、创建项目时不再支持 maven 选项 2、必须是 jdk17 及以后版本(点击查看官网版本对应关系&…...
极速文件搜索工具Everything结合内网穿透实现远程搜索本地文件
文章目录 前言1.软件安装完成后,打开Everything2.登录cpolar官网 设置空白数据隧道3.将空白数据隧道与本地Everything软件结合起来总结 前言 要搭建一个在线资料库,我们需要两个软件的支持,分别是cpolar(用于搭建内网穿透数据隧道…...

【PowerMockito:编写单元测试过程中采用when打桩失效的问题】
问题描述 正如上图所示,采用when打桩了,但是,实际执行的时候还是返回null。 解决方案 打桩时直接用any() 但是这样可能出现一个mybatisplus的异常,所以在测试类中需要加入以下代码片段: Beforepublic void setUp() …...

[蓝桥杯 2018省赛]回家路费
回家路费 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小明被不明势力劫持。后莫名其妙被扔到 X 星站再无问津。小明得知每天都有飞船飞往地球,但需要 108108 元的船票,而他却身无分文。…...
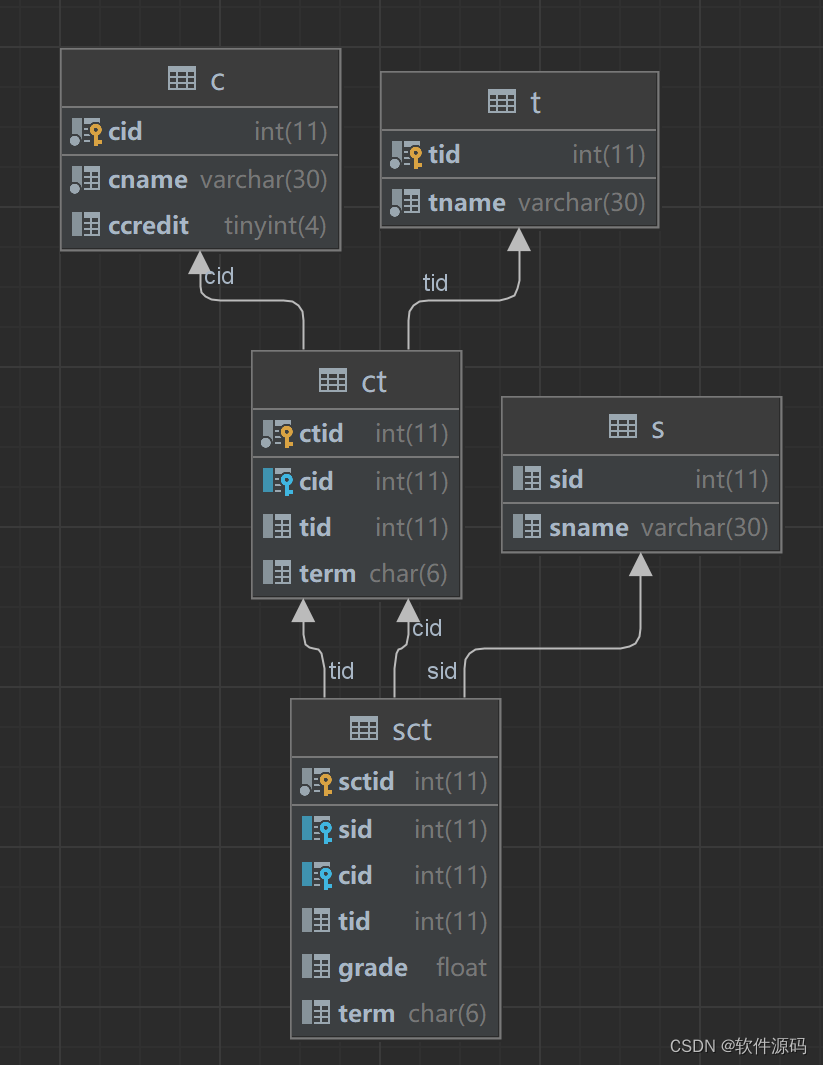
学生管理系统(vue + springboot)
学生管理系统(vuespringboot)资源-CSDN文库 项目介绍 这是一个采用前后端分离开发的项目,前端采用 Vue 开发、后端采用 Spring boot Mybatis 开发。 项目部署 ⭐️如果你有 docker 的话,直接 docker compose up 即可启动&#…...

算法(3)——二分查找
一、什么是二分查找 二分查找也称折半查找,是在一组有序(升序/降序)的数据中查找一个元素,它是一种效率较高的查找方法。 二、二分查找的原理 1、查找的目标数据元素必须是有序的。没有顺序的数据,二分法就失去意义。 2、数据元素通常是数值…...

golang实现可中断的流式下载
golang实现可中断的流式下载 最近有一个需要实现下载功能: 从服务器上读取文件,返回一个ReadCloser在用户磁盘上创建文件,通过io.Copy实现文件下载(io.Copy是流式的操作,不会出现因文件过大而内存暴涨的问题࿰…...
SpringBoot 医药咨询系统
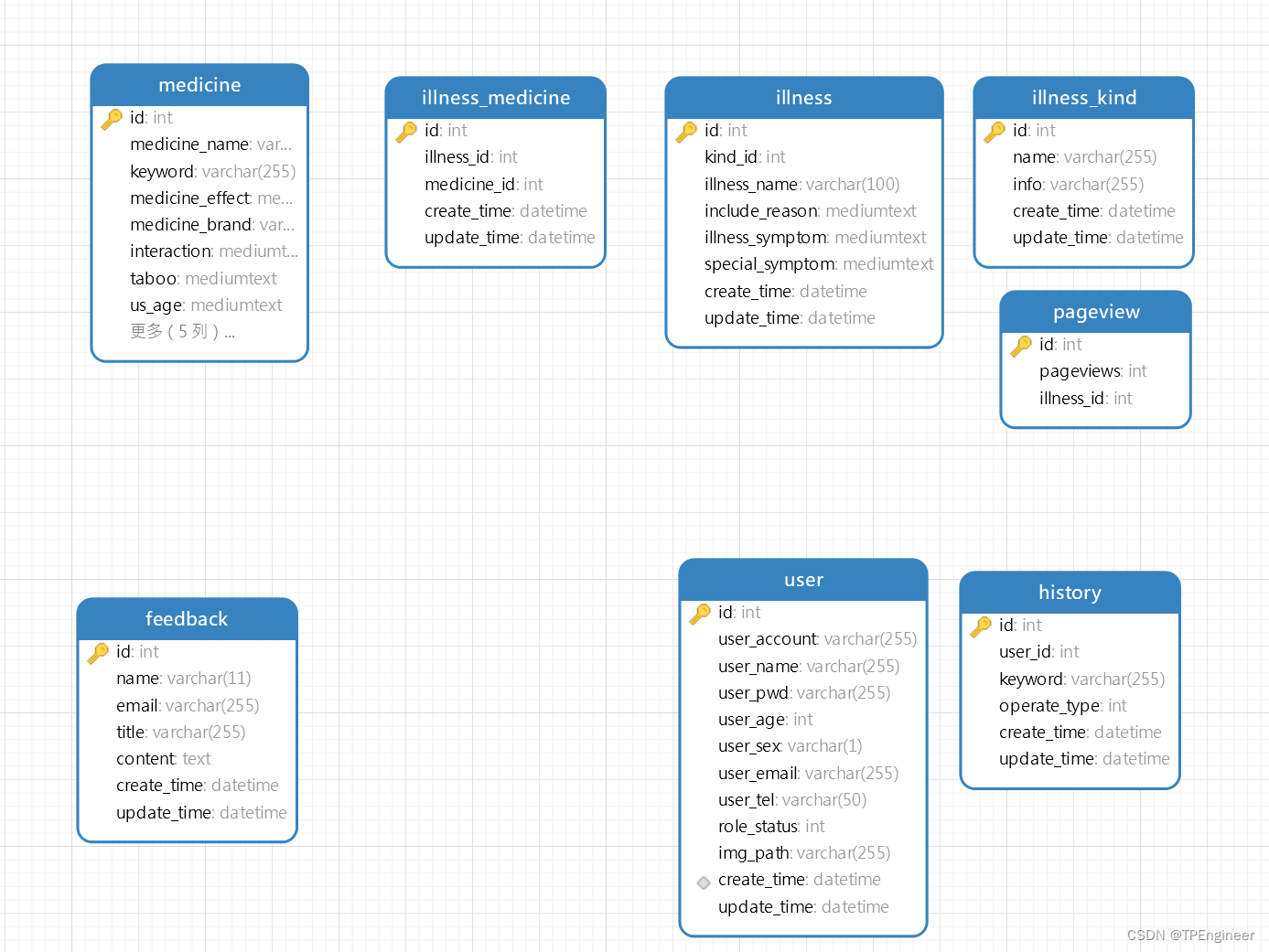
概述 智慧医药系统(smart-medicine)是一个基于 SpringBoot 开发的Web 项目。整体页面简约大气,增加了AI医生问诊功能,功能设计的较为简单。 开源地址 https://gitcode.net/NVG_Haru/Java_04 界面预览 功能介绍 游客功能介绍 …...
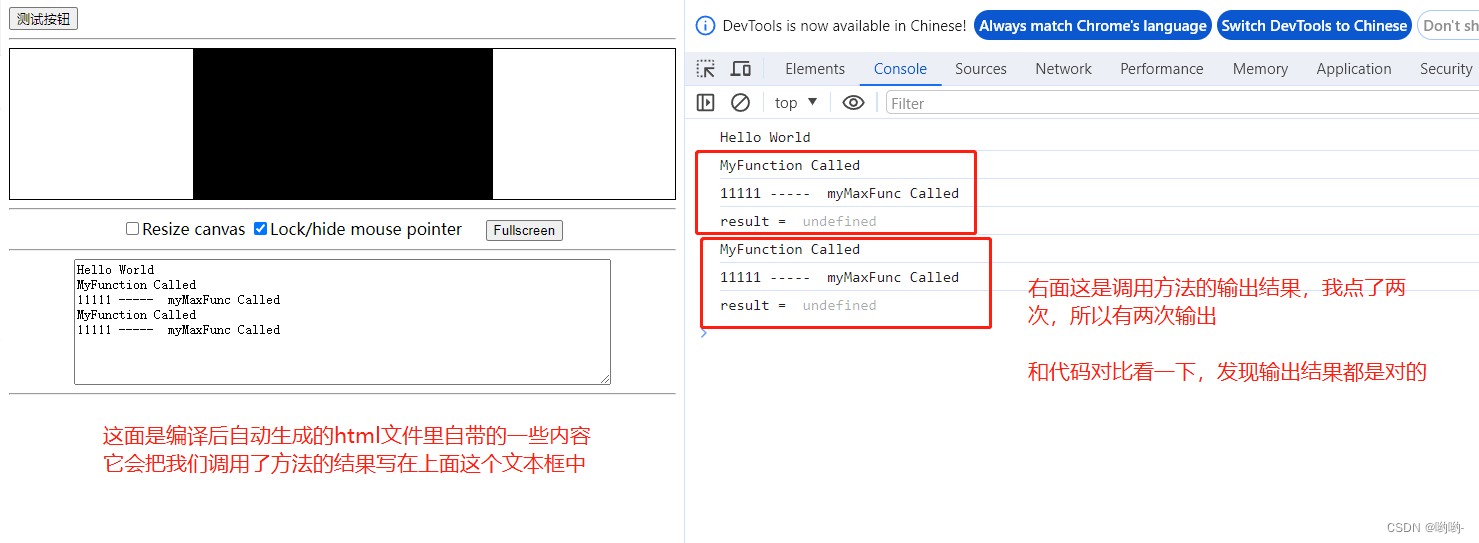
C语言转WebAssembly的全流程,及Web端调用测试
第一步:安装环境 参考网址:https://emscripten.org/docs/getting_started/downloads.html 具体过程: 克隆代码:git clone https://github.com/emscripten-core/emsdk.git进入代码目录:cd emsdk获取最新远端代码&…...
前端--基础 目录文件夹和根目录 VScode打开目录文件夹
目录 目录文件夹和根目录 : 目录文件夹 : 根目录 : VScode 打开目录文件夹 : VScode 打开文件夹 : 拖拽目录文件夹 : 目录文件夹和根目录 : 我们都清楚,在实际的工作中会…...

传感器原理与应用复习--超声波、微波、红外及热电偶传感器
文章目录 上一篇超声波传感器微波传感器红外传感器热电偶传感器下一篇 上一篇 传感器原理与应用复习–光电式与半导体式传感器 超声波传感器 超过2万赫兹以上的波称为超声波 压电式超声波探头常用材料是压电晶体和压电陶瓷。它是利用压电材料的压电效应来工作的。 逆压电效…...
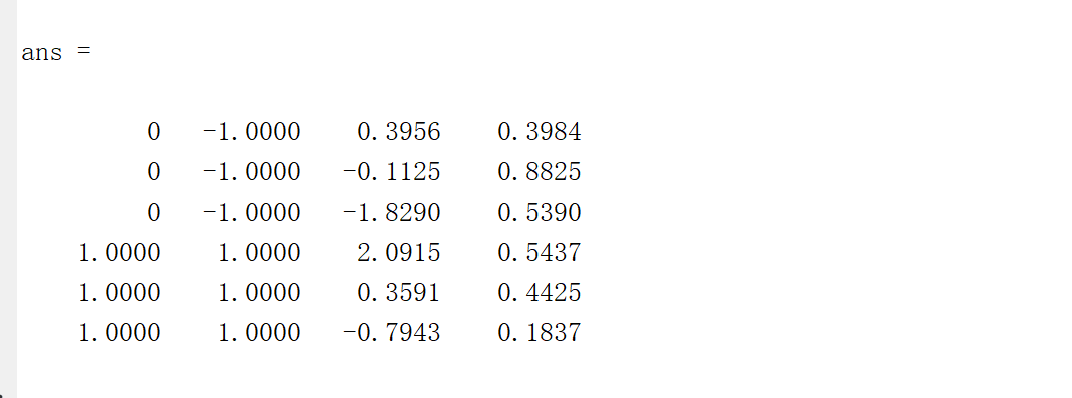
matlab概率论例子
高斯概率模型: [f,xi] ksdensity(x): returns a probability density estimate, f, for the sample in the vector x. The estimate is based on a normal kernel function, and is evaluated at 100 equally spaced points, xi, that cover the range of the da…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
