算法(3)——二分查找
一、什么是二分查找
二分查找也称折半查找,是在一组有序(升序/降序)的数据中查找一个元素,它是一种效率较高的查找方法。
二、二分查找的原理
1、查找的目标数据元素必须是有序的。没有顺序的数据,二分法就失去意义。
2、数据元素通常是数值型,可以比较大小。
3、将目标元素和查找范围的中间值做比较(如果目标元素=中间值,查找结束),将目标元素分到较大/或者较小的一组。
4、通过分组,可以将查找范围缩小一半。
5、重复第三步,直到目标元素=新的范围的中间值,查找结束。
三、二分查找模板
1、朴素二分查找模板

2、一般二分查找模板
四、二分查找经典OJ题
4、1 二分查找
704. 二分查找 - 力扣(LeetCode)
1、题目描述

2、算法思路
a. 定义 left , right 指针,分别指向数组的左右区间。b. 找到待查找区间的中间点 mid ,找到之后分三种情况讨论:i. arr[mid] == target 说明正好找到,返回 mid 的值ii. arr[mid] > target 说明 [mid, right] 这段区间都是⼤于 target 的,因此舍去右边区间,在左边 [left, mid -1] 的区间继续查找,即让 right = mid - 1 ,然后重复 2 过程;
iii. arr[mid] < target 说明 [left, mid] 这段区间的值都是⼩于 target 的,因此舍去左边区间,在右边 [mid + 1, right] 区间继续查找,即让 left = mid + 1 ,然后重复 2 过程;c. 当 left 与 right 错开时,说明整个区间都没有这个数,返回 -1 。
3、算法代码
class Solution {
public:int search(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<=right){int mid=left+(right-left)/2;if(nums[mid]>target){right=mid-1;}else if(nums[mid]<target){left=mid+1;}else{return mid;}}return -1;}
};4、2 在排序数组中查找元素的第⼀个和最后⼀个位置
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
1、题目描述:

2、算法思路:
寻找左边界:◦ 我们注意到以左边界划分的两个区间的特点:▪ 左边区间 [left, resLeft - 1] 都是⼩于 x 的;▪ 右边区间(包括左边界) [resLeft, right] 都是⼤于等于 x 的;• 因此,关于 mid 的落点,我们可以分为下⾯两种情况:◦ 当我们的 mid 落在 [left, resLeft - 1] 区间的时候,也就是 arr[mid] < target 。说明 [left, mid] 都是可以舍去的,此时更新 left 到 mid + 1 的位置, 继续在 [mid + 1, right] 上寻找左边界;◦ 当 mid 落在 [resLeft , right] 的区间的时候,也就是 arr[mid] >= target 。 说明 [mid + 1, right] (因为 mid 可能是最终结果,不能舍去)是可以舍去的,此时 更新 right 到 mid 的位置,继续在 [left, mid] 上寻找左边界;• 由此,就可以通过⼆分,来快速寻找左边界;
注意:这⾥找中间元素需要向下取整。因为后续移动左右指针的时候:• 左指针: left = mid + 1 ,是会向后移动的,因此区间是会缩⼩的;• 右指针: right = mid ,可能会原地踏步(⽐如:如果向上取整的话,如果剩下 1,2 两个元素, left == 1 , right == 2 , mid == 2 。更新区间之后, left , right , mid 的 值没有改变,就会陷⼊死循环)。因此⼀定要注意,当 right = mid 的时候,要向下取整。
寻找右边界思路:◦ ⽤ resRight 表⽰右边界;◦ 我们注意到右边界的特点:▪ 左边区间 (包括右边界) [left, resRight] 都是⼩于等于 x 的;▪ 右边区间 [resRight+ 1, right] 都是⼤于 x 的;• 因此,关于 mid 的落点,我们可以分为下⾯两种情况:◦ 当我们的 mid 落在 [left, resRight] 区间的时候,说明 [left, mid - 1](mid 不可以舍去,因为有可能是最终结果) 都是可以舍去的,此时更新 left 到 mid 的位置;◦ 当 mid 落在 [resRight+ 1, right] 的区间的时候,说明 [mid, right] 内的元素 是可以舍去的,此时更新 right 到 mid - 1 的位置;• 由此,就可以通过⼆分,来快速寻找右边界;
注意:这⾥找中间元素需要向上取整。因为后续移动左右指针的时候:• 左指针: left = mid ,可能会原地踏步(⽐如:如果向下取整的话,如果剩下 1,2 两个元素, left == 1 , right == 2 , mid == 1 。更新区间之后, left , right , mid 的值 没有改变,就会陷⼊死循环)。• 右指针: right = mid - 1 ,是会向前移动的,因此区间是会缩⼩的; 因此⼀定要注意,当 right = mid 的时候,要向下取整。
3、算法代码
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int begin=0;if(nums.size()==0) return {-1,-1};int left=0,right=nums.size()-1;while(right>left) //找左端点{int mid=left+(right-left)/2;if(nums[mid]<target) left=mid+1;else right=mid;}if(nums[left]!=target) return {-1,-1};else begin=left;left=0,right=nums.size()-1;while(right>left){int mid=left+(right-left+1)/2;if(nums[mid]<=target) left=mid;else right=mid-1;}return {begin,right};}
};4、3 搜索插入位置
35. 搜索插入位置 - 力扣(LeetCode)
1、题目描述

2、算法思路
a. 分析插⼊位置左右两侧区间上元素的特点:设插⼊位置的坐标为 index ,根据插⼊位置的特点可以知道:• [left, index - 1] 内的所有元素均是⼩于 target 的;• [index, right] 内的所有元素均是⼤于等于 target 的。b. 设 left 为本轮查询的左边界, right 为本轮查询的右边界。根据 mid 位置元素的信息,分析下⼀轮查询的区间:▪ 当 nums[mid] >= target 时,说明 mid 落在了 [index, right] 区间上,mid 左边包括 mid 本⾝,可能是最终结果,所以我们接下来查找的区间在 [left, mid] 上。因此,更新 right 到 mid 位置,继续查找。▪ 当 nums[mid] < target 时,说明 mid 落在了 [left, index - 1] 区间上, mid 右边但不包括 mid 本⾝,可能是最终结果,所以我们接下来查找的区间在 [mid + 1, right] 上。因此,更新 left 到 mid + 1 的位置,继续查找。c. 直到我们的查找区间的⻓度变为 1 ,也就是 left == right 的时候, left 或者right 所在的位置就是我们要找的结果。
3、算法代码
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(right>left){int mid=left+(right-left)/2;if(nums[mid]<target) left=mid+1;else right=mid;}if(nums[left]<target) return right+1;return right;}
};4、4 X的平方根
69. x 的平方根 - 力扣(LeetCode)
1、题目描述

2、算法思路
依次枚举 [0, x] 之间的所有数 i :(这⾥没有必要研究是否枚举到 x / 2 还是 x / 2 + 1 。因为我们找到结果之后直接就返回了,往后的情况就不会再判断。反⽽研究枚举区间,既耽误时间,⼜可能出错)▪ 如果 i * i == x ,直接返回 x ;▪ 如果 i * i > x ,说明之前的⼀个数是结果,返回 i - 1 。由于 i * i 可能超过 int 的最⼤值,因此使⽤ long long 类型
3、算法代码
class Solution {
public:int mySqrt(int x) {if(x<1) return 0;int left=1,right=x;while(right>left){long long mid=left+(right-left+1)/2;if(mid*mid>x) right=mid-1;else left=mid;}return left;}
};4、5 山峰数组的峰顶
852. 山脉数组的峰顶索引 - 力扣(LeetCode)
1、题目描述

2、算法思路
class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {for(int i=1;i<arr.size()-1;i++){if(arr[i]>arr[i-1]&&arr[i]>arr[i+1]){return i;} }return 0;}
};4、5 寻找峰值
162. 寻找峰值 - 力扣(LeetCode)
1、题目描述

2、算法思路寻找⼆段性:
class Solution {
public:int findPeakElement(vector<int>& nums) {vector<int> ret;int left=0,right=nums.size()-1;while(right>left){int mid=left+(right-left+1)/2;if(nums[mid]>nums[mid-1]) left=mid;else right=mid-1;}return left;}
};4、6 寻找旋转排序数组中的最⼩值
153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)
1、题目描述

2、算法思路

class Solution {
public:int findMin(vector<int>& nums) {int tmp=nums[nums.size()-1];int left=0,right=nums.size()-1;while(right>left){int mid=left+(right-left)/2;if(nums[mid]>tmp) left=mid+1;else right=mid;}return nums[left];}
};4、7 0~n-1缺失的数字
LCR 173. 点名 - 力扣(LeetCode)
1、题目描述

2、算法思路
class Solution {
public:int takeAttendance(vector<int>& records) {int left=0,right=records.size()-1,k=0;while(right>left){int mid = left+(right-left)/2;if(records[mid]!=mid) right=mid;else left=mid+1;}return left==records[left]?left+1:left;}
相关文章:

算法(3)——二分查找
一、什么是二分查找 二分查找也称折半查找,是在一组有序(升序/降序)的数据中查找一个元素,它是一种效率较高的查找方法。 二、二分查找的原理 1、查找的目标数据元素必须是有序的。没有顺序的数据,二分法就失去意义。 2、数据元素通常是数值…...

golang实现可中断的流式下载
golang实现可中断的流式下载 最近有一个需要实现下载功能: 从服务器上读取文件,返回一个ReadCloser在用户磁盘上创建文件,通过io.Copy实现文件下载(io.Copy是流式的操作,不会出现因文件过大而内存暴涨的问题࿰…...
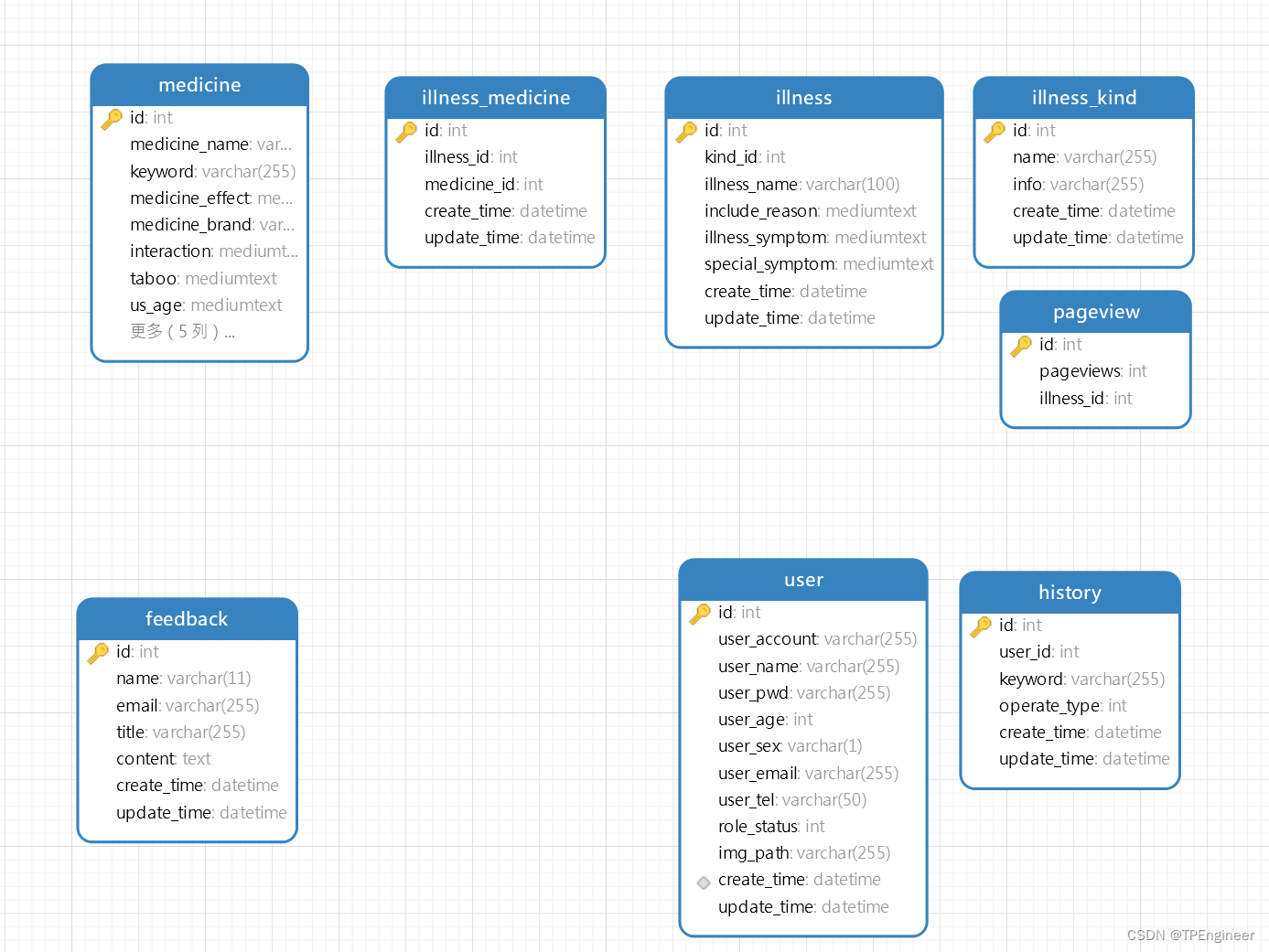
SpringBoot 医药咨询系统
概述 智慧医药系统(smart-medicine)是一个基于 SpringBoot 开发的Web 项目。整体页面简约大气,增加了AI医生问诊功能,功能设计的较为简单。 开源地址 https://gitcode.net/NVG_Haru/Java_04 界面预览 功能介绍 游客功能介绍 …...
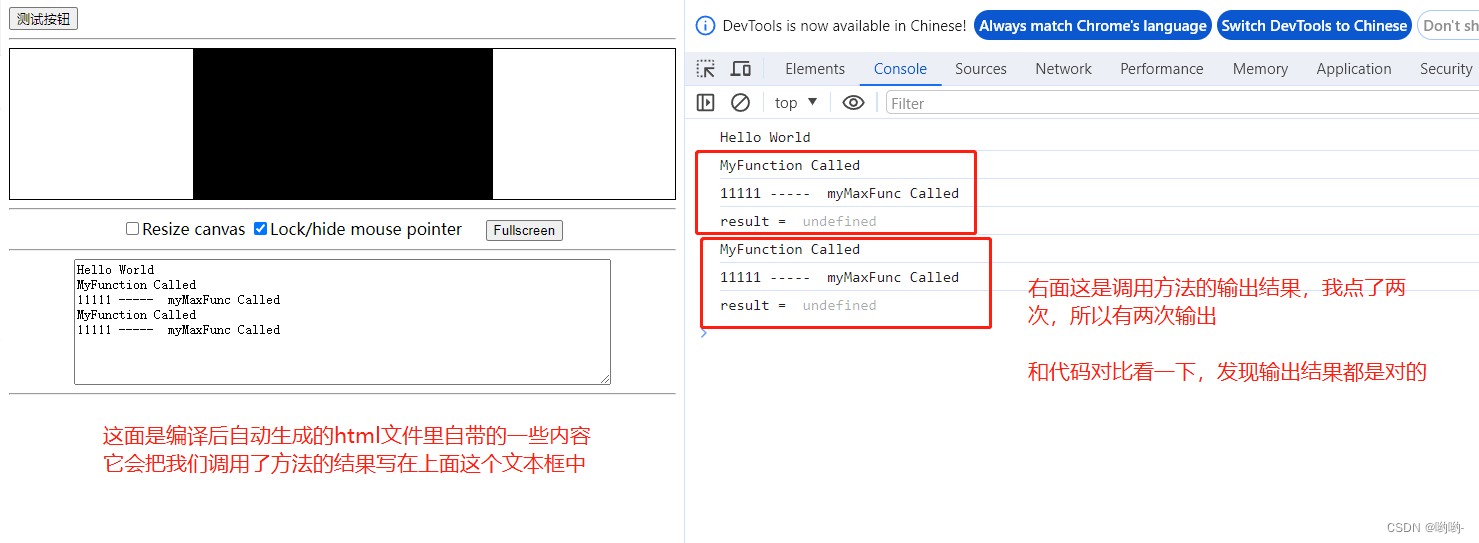
C语言转WebAssembly的全流程,及Web端调用测试
第一步:安装环境 参考网址:https://emscripten.org/docs/getting_started/downloads.html 具体过程: 克隆代码:git clone https://github.com/emscripten-core/emsdk.git进入代码目录:cd emsdk获取最新远端代码&…...
前端--基础 目录文件夹和根目录 VScode打开目录文件夹
目录 目录文件夹和根目录 : 目录文件夹 : 根目录 : VScode 打开目录文件夹 : VScode 打开文件夹 : 拖拽目录文件夹 : 目录文件夹和根目录 : 我们都清楚,在实际的工作中会…...

传感器原理与应用复习--超声波、微波、红外及热电偶传感器
文章目录 上一篇超声波传感器微波传感器红外传感器热电偶传感器下一篇 上一篇 传感器原理与应用复习–光电式与半导体式传感器 超声波传感器 超过2万赫兹以上的波称为超声波 压电式超声波探头常用材料是压电晶体和压电陶瓷。它是利用压电材料的压电效应来工作的。 逆压电效…...
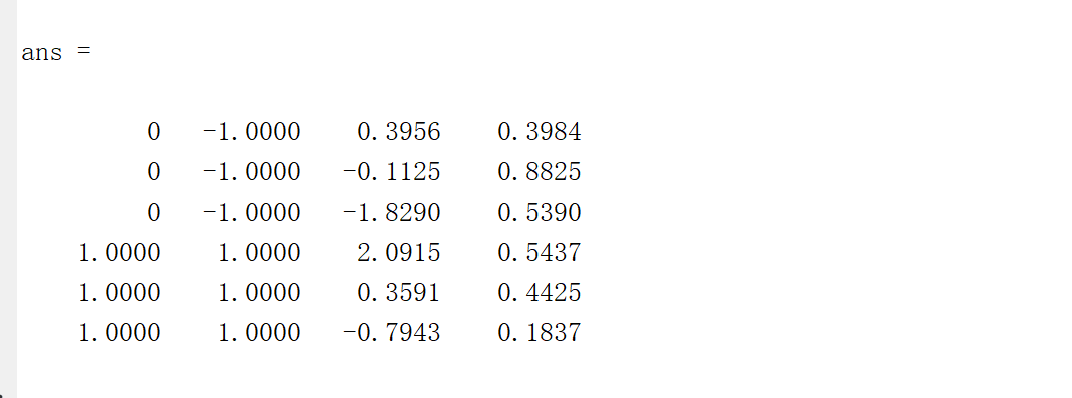
matlab概率论例子
高斯概率模型: [f,xi] ksdensity(x): returns a probability density estimate, f, for the sample in the vector x. The estimate is based on a normal kernel function, and is evaluated at 100 equally spaced points, xi, that cover the range of the da…...

Appium+python自动化(一)- 环境搭建—上(超详解)
简介 今天是高考各地由于降水,特别糟糕,各位考生高考加油,全国人民端午节快乐。最近整理了一下自动化的东西,先前整理的python接口自动化已经接近尾声。即将要开启新的征程和篇章(Appium&python)。那么…...

基于SpringBoot的精简博客系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的精简博客系统,java项目…...
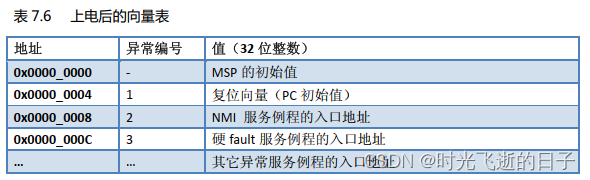
STM32的在线升级(IAP)实现方法:BOOT+APP原理详解
0 工具准备 Keil uVision5 Cortex M3权威指南(中文) STM32参考手册 1 在线升级(IAP)设计思路 为了实现STM32的在线升级(IAP)功能,通常会将STM32的FLASH划分为BOOT和APP两个部分,BOO…...

【芯片DFX】Arm调试架构篇
【芯片DFX】万字长文带你搞懂JTAG的门门道道【芯片DFX】ARM:CoreSight、ETM、PTM、ITM、HTM、ETB等常用术语解析...
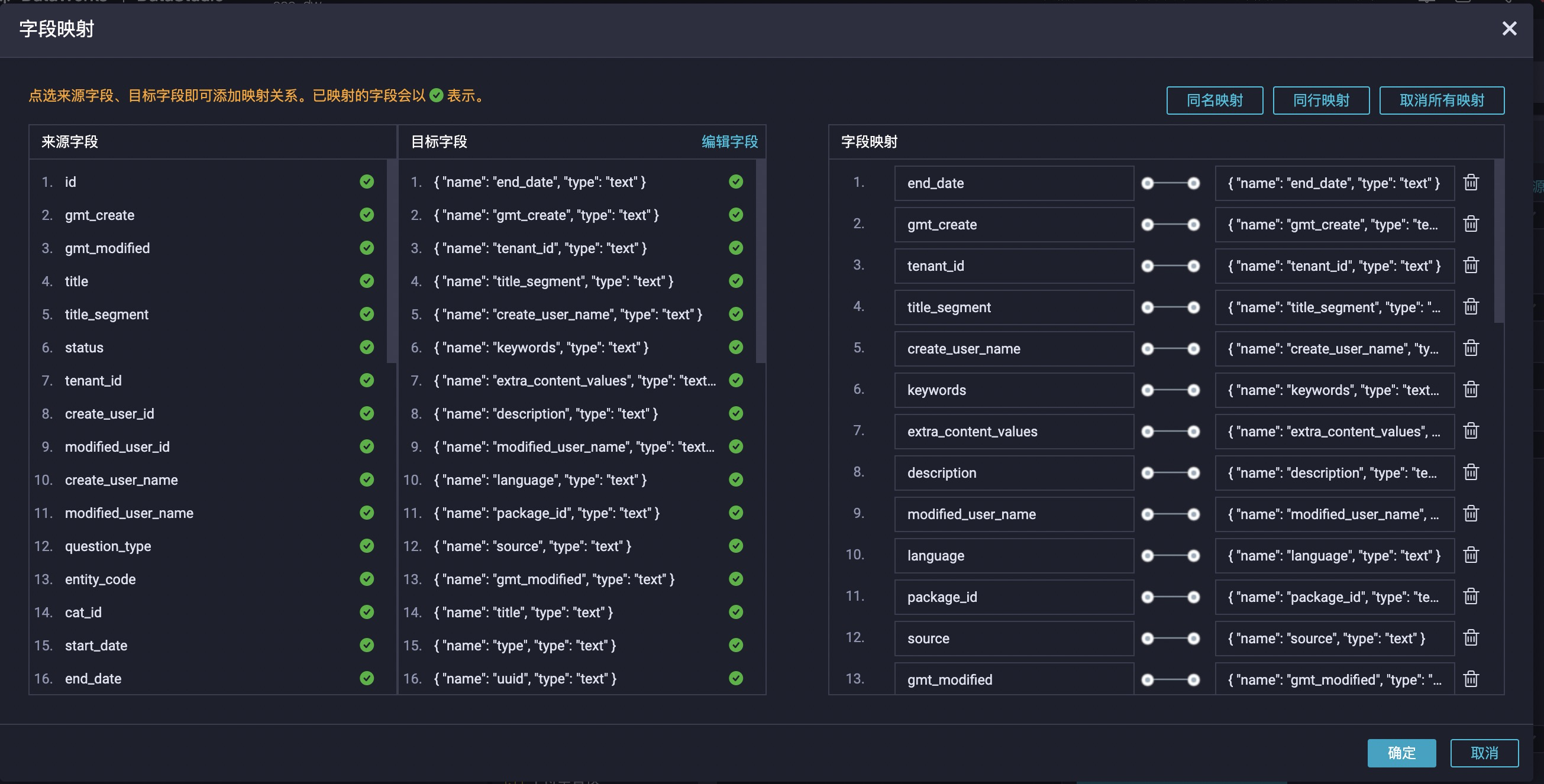
ES应用_ES实战
依靠知识库使用es总结一些使用技巧。 1 快速入门 ES是将查询语句写成类似json的形式,通过关键字进行查询和调用。 1.1 创建 下面创建了一个主分片为5,副本分片为1的ES结构。ES本身是一种noschema的结构,但是可以通过指定mapping编程schema的…...

Ubuntu上如何找到设备,打印串口日志
dmesg 找设备 sudo mincom -s 配置minicom mincom 打印串口日志 PS: Windows上使用MobaXterm / putty / Xshell / SecureCRT等 ubuntu串口的安装和使用(usb转串口)_ubuntu上如何把usb设备映射到tty-CSDN博客...

本地映射测试环境域名,解决登录测试环境后,也可以使用本地域名访问,可以正常跑本地项目
问题:单点登录进入系统不使用token,是将token携带在cookie中,登录成功后每次调用接口,都会在cookie中自动携带,这样导致即使在本地使用proxy代理解决了跨域,但由于本地域名不一致,也无法进行本地…...
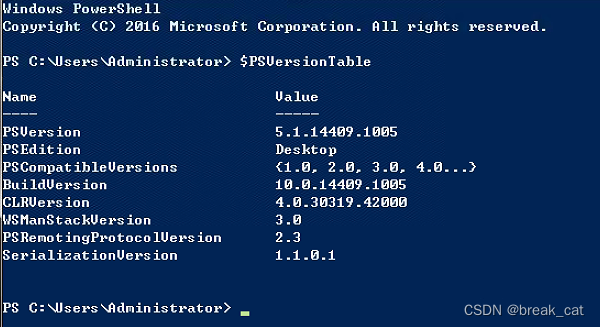
VSCode使用Remote SSH远程连接Windows 7
结论 VSCode Server不能启动,无法建立连接。 原因 .vscode-server 目录中的 node.exe 无法运行。 原因是Node.js仅在Windows 8.1、Windows Server 2012 R2或更高版本上受支持。 由于vscode基于node.js v14,不支持Windows 7操作系统。 另ÿ…...

uniapp中uview组件库丰富的Calendar 日历用法
目录 基本使用 #日历模式 #单个日期模式 #多个日期模式 #日期范围模式 #自定义主题颜色 #自定义文案 #日期最大范围 #是否显示农历 #默认日期 基本使用 通过show绑定一个布尔变量用于打开或收起日历弹窗。通过mode参数指定选择日期模式,包含单选/多选/范围…...
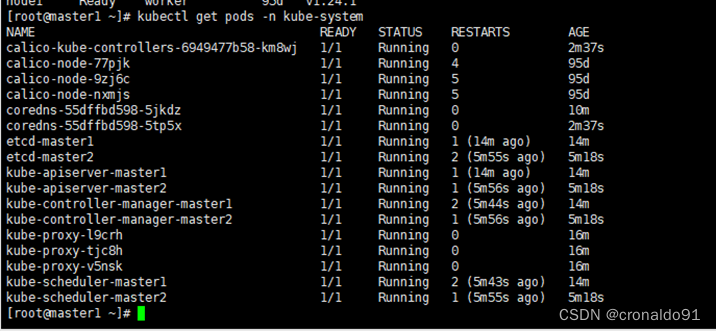
云原生Kubernetes:K8S集群实现容器运行时迁移(docker → containerd) 与 版本升级(v1.23.14 → v1.24.1)
目录 一、理论 1.K8S集群升级 2.环境 3.升级策略 4.master1节点迁移容器运行时(docker → containerd) 5.master2节点迁移容器运行时(docker → containerd) 6.node1节点容器运行时迁移(docker → containerd) 7.升级集群计划(v1.23.14 → v1.24.1&#…...

Redis 数据结构和常用命令
* 代表多个,?代表一个 (不用全部敲出来,按住tab可以自动补全) -2是无效,-1是永久有效 ;贴心小提示:内存非常宝贵,对于一些数据,我们应当给他一些过期时间&a…...

Docker 容器命令总汇
目录 1、创建Docker容器(不启动) 2、创建Docker容器(启动) 3、列出正在运行的容器 4、停止和启动容器 5、重启容器 6、进入容器 7、查看容器信息 8、查看容器日志 9、删除容器和镜像 10、重命名容器 11、从旧容器复制数…...
react + redux 之 美团案例
1.案例展示 2.环境搭建 克隆项目到本地(内置了基础静态组件和模版) git clone http://git.itcast.cn/heimaqianduan/redux-meituan.git 安装所有依赖 npm i 启动mock服务(内置了json-server) npm run serve 启动前端服务 npm…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
