可爱的魔法曲线 Lovely Magical Curves(12年开始只有5个人AC)
一起来交流编程吧!【CSDN app】:http://qm.qq.com/cgi-bin/qm/qr?_wv=1027&k=3svdDJTlkD76TRRShbxYCYK1zK1c8cyF&authKey=v1pxp6rS8AA4SRy7bflJl9LIwp8d5v0HOudw%2BDxHiWDRqZ1LzjeoBJH1Z1EXnl35&noverify=0&group_code=546881376
可爱的魔法曲线 Lovely Magical Curves
题面翻译
题目描述
NURBS 曲线由一系列参数点定义,它的函数如下:
C ( u ) = ∑ i = 1 n w i N i , k ( u ) P i ∑ i = 1 n w i N i , k ( u ) C(u)=\dfrac{\sum_{i=1}^nw_iN_{i,k}(u)P_i}{\sum_{i=1}^nw_iN_{i,k}(u)} C(u)=∑i=1nwiNi,k(u)∑i=1nwiNi,k(u)Pi
而 u u u 是参数, n n n 是控制点的个数, k k k 是曲线的度数, P i P_i Pi 是控制点的位置, w i w_i wi 是控制点的权重。
N i , k N_{i,k} Ni,k 这样递归的定义:
N i , k ( u ) = u − t i t i + k − t i N i , k − 1 ( u ) + t i + k + 1 − u t i + k + 1 − t i + 1 N i + 1 , k − 1 ( u ) N_{i,k}(u)=\frac{u-t_i}{t_{i+k}-t_i}N_{i,k-1}(u)+\frac{t_{i+k+1}-u}{t_{i+k+1}-t_{i+1}}N_{i+1,k-1}(u) Ni,k(u)=ti+k−tiu−tiNi,k−1(u)+ti+k+1−ti+1ti+k+1−uNi+1,k−1(u)
N i , 0 ( u ) = [ t i ≤ u < t i + 1 ] N_{i,0}(u)=[t_i\le u<t_{i+1}] Ni,0(u)=[ti≤u<ti+1]
而 t i t_i ti 是第 i i i 个节。在本题中 0 / 0 = 0 \mathbf{0/0=0} 0/0=0。
为解释如上的恐怖公式,下面我们解释如上的参数。
- 度数。 度数 k k k 是一个正整数。在 NURBS 中,直线的度数是 1 1 1,圆的是 2 2 2,有趣的曲线是 3 3 3 或者 5 5 5。
- 控制点。 控制点至少有 k + 1 k+1 k+1 个。改变 NURBS 曲线的最简方式是移动控制点。任何一个控制点都有一个权重 w i w_i wi,在本题中权重是正整数。如果一个点的权重更大,则曲线被“吸”像该控制点。
- 节。 节向量的定义是 U = [ t 1 , t 2 , ⋯ , t m ] U=[t_1,t_2,\cdots,t_m] U=[t1,t2,⋯,tm]。 m , k , n m,k,n m,k,n 的关系是 m = n + k + 1 m=n+k+1 m=n+k+1。节向量的相邻两项元素都满足 t i ≤ t i + 1 t_i\le t_{i+1} ti≤ti+1。每一组相邻的节代表一个参数值区间 [ t i , t i + 1 ) [t_i,t_{i+1}) [ti,ti+1) 用以计算曲线的形状。因此,曲线的定义域是 [ t 1 , t m ) \mathbf{[t_1,t_m)} [t1,tm)。 节值的重复次数是其倍率,且小于度数。节值的重复次数会减小曲线的平滑度。
如果你还是没有看懂,我们这里建议把 u u u 从 t 1 t_1 t1 到 t m t_m tm 移动(但不要等于 t m t_m tm),你就会看到 C ( u ) C(u) C(u) 按照曲线所在的位置移动。
你的任务:求出两条 NURBS 曲线的交点。
输入格式
T T T 组数据。
每组数据包含两部分,分别描述两条 NURBS 曲线。每条曲线的开头是两个整数 n , m ( 2 ≤ n ≤ 20 ) n,m(2\le n\le 20) n,m(2≤n≤20),而后 n n n 行每行三个实数 x , y , w ( 0 ≤ x , y ≤ 10 , 0 < w ≤ 10 ) x,y,w(0\le x,y\le 10,0<w\le 10) x,y,w(0≤x,y≤10,0<w≤10) 代表控制点 P i ( x , y ) , w i P_i(x,y),w_i Pi(x,y),wi。而后一行是 m m m 个实数,即节向量。第一个节值永远是 0 0 0 并且最后一个永远是 1 1 1。度数永远是 1 , 2 , 3 , 5 1,2,3,5 1,2,3,5 中之一。
输出格式
第一行一个数即交点个数。各个交点应四舍五入到小数点后三位,并且每个点应按照字典序排列(即从小到大,先 x x x 后 y y y)。输入是专门设计的,以满足最小的交点的 x x x 坐标只差最少为 0.005 0.005 0.005。
对于每组数据,在末尾输出一个空行。
题目描述

输入格式

输出格式

样例 #1
样例输入 #1
2
8 12
2 01
0 11
1 32
1.5 2 1
2.5 2 1
3 32
4 11
2 01
0 0 0 0 0.2 0.4 0.6 0.8 1 1 1 1
2 4
0 0 1
4 3 1
0 0 1 1
7 10
1 1.732 1
0 0 0.5
2 0 1
4 0 0.5
3 1.732 1
2 3.464 0.5
1 1.732 1
0 0 0 0.333 0.333 0.667 0.667 1 1 1
7 10
0 1.732 1
2 0 0.5
3 0 1
6 0 0.5
2 1.732 1
6 3.464 0.5
0 1.732 1
0 0 0 0.333 0.333 0.667 0.667 1 1 1
样例输出 #1
Case 1: 2
(1.029, 0.772)
(3.221, 2.416)
Case 2: 6
(0.847, 1.092)
(1.307, 2.078)
(2.283, 2.274)
(2.538, 0.133)
(2.693, 2.078)
(3.153, 1.092)
大佬的指点
题意简述
给定两条 NURBS 曲线,求它们的交点。
题目思路
首先,需要注意的是种种奇奇怪怪东西的定义。
第一就是公式:
C(u)=∑i=1nwiNi,k(u)Pi∑i=1nwiNi,k(u)C(u)=\dfrac{\sum_{i=1}^nw_iN_{i,k}(u)P_i}{\sum_{i=1}^nw_iN_{i,k}(u)} C(u)=∑i=1nwiNi,k(u)∑i=1nwiNi,k(u)Pi
它的意思就是说,我们可以把如上的这些点和它的函数以及权重相乘,而后我们需要一些比较新奇的理解,即把所有的 PiP_iPi 的两个坐标加起来,而后除以下面的一大坨东西。
而后,我们观察一下这个多项式函数:
Ni,k(u)=u−titi+k−tiNi,k−1(u)+ti+k+1−uti+k+1−ti+1Ni+1,k−1(u)N_{i,k}(u)=\frac{u-t_i}{t_{i+k}-t_i}N_{i,k-1}(u)+\frac{t_{i+k+1}-u}{t_{i+k+1}-t_{i+1}}N_{i+1,k-1}(u) Ni,k(u)=ti+k−tiu−tiNi,k−1(u)+ti+k+1−ti+1ti+k+1−uNi+1,k−1(u)
Ni,0(u)=[ti≤u<ti+1]N_{i,0}(u)=[t_i\le u<t_{i+1}] Ni,0(u)=[ti≤u<ti+1]
它的意思,已经被直白的表述在了公式之中,因此不解释。
因此,这是第一版代码中 NURBS 曲线的定义:
struct nurbs{int n; // numbers of control pointsint k; // degreeint m; // number of knotspoint P[25]; // control pointsdouble w[25]; // weight of pointsdouble t[25]; // knot vectordouble N(int i,int k,double u){ // Function Nif(k==0) return (t[i]<=u&&u<t[i+1]?1.0:0.0);double co0,co1;if(fabs(t[i+k]-t[i])<EPS||fabs(u-t[i])<EPS) co0=0;else co0=(u-t[i])/(t[i+k]-t[i]);if(fabs(t[i+k+1]-u)<EPS||fabs(t[i+k+1]-t[i+1])<EPS) co1=0;else co1=(t[i+k+1]-u)/(t[i+k+1]-t[i+1]);return co0*N(i,k-1,u)+co1*N(i+1,k-1,u);}point C(double u){ // Function C (for a single curve)point num=point(0,0);double dem=0;for(int i=1;i<=n;i++){num=num+w[i]*N(i,k,u)*P[i];dem+=w[i]*N(i,k,u);}return num/dem;}void clear(){n=k=m=0;for(int i=0;i<25;i++) P[i].x=P[i].y=w[i]=t[i]=0;}
}curv[3];
当然,多测不清空的悲剧还是要尽量避免,因此有一个 clear() 在这里。
另外,题目加粗强调了 0/0=00/0=00/0=0,但是我要告诉你的是,x/yx/yx/y 中只要 x=0x=0x=0 或者 y=0y=0y=0 那么这个式子就等于 000,不等于任何别的数!
于是,我们当然可以把第一版程序中点结构体拿出来:
const double EPS=8e-5;
struct point{double x,y;point(double cx=0,double cy=0):x(cx),y(cy){}
};
point operator*(double a,point p){return point(p.x*a,p.y*a);
}
point operator+(point a,point b){return point(a.x+b.x,a.y+b.y);
}
point operator/(point a,double b){double x=a.x/b,y=a.y/b;if(fabs(a.x)<EPS||fabs(b)<EPS) x=0;if(fabs(a.y)<EPS||fabs(b)<EPS) y=0;return point(x,y);
}
好的,我们就可以通过暴力枚举 [0,1)[0,1)[0,1) 里的非常多的点来找到交点,如果要找到交点,可以直接用 set 里的 intersection。
但是,如果这样的话,你大概率会那道一个 WA 或者 RE 或者 TLE。
那么我们应该怎么办?
众所周知,我们可以通过把曲线近似为很多条线段(亦即折线)来达到相同的结果,因此,我们可以设一个非常大的正整数 RRR,而后设 s=1/Rs=1/Rs=1/R,随后对于 k=0⋯(R−1)k=0\cdots(R-1)k=0⋯(R−1),或者说只要 ks≠1ks\neq 1ks=1,我们就能找到点 C(ks)C(ks)C(ks),并且把相邻的两个点用线段连接起来。
这是不需要多说的,因为下面就要开始让人心肺骤停了。
首先的问题是:如何求得两条线段的交点,而它的简化方式,就是求出直线的交点。我们可以设两条直线分别为 P+tv→P+t\overrightarrow{v}P+tv 和 Q+tw→Q+t\overrightarrow{w}Q+tw,而后设 u→=P−Q\overrightarrow{u}=P-Qu=P−Q,然后通过解方程(过程略),我们就能得出交点的位置在
P+(w→×u→v→×w→)v→P+\left(\frac{\overrightarrow{w}\times\overrightarrow{u}}{\overrightarrow{v}\times\overrightarrow{w}}\right)\overrightarrow{v} P+(v×ww×u)v
这样我们就可以给出这样的一份代码求两条直线的交点:
point getintersection(point p,vecto v,point q,vecto w){vecto u=p-q;double t=cross(w,u)/cross(v,w);return p+v*t;
}
那么,我们现在研究线段的相交,它的充分必要条件就是,每条线段的两个端点都在另一条线段的两侧(即叉积的符号不同)。因此我们这样写出:
bool isintersected(point a1,point a2,point b1,point b2){double c1=cross(a2-a1,b1-a1),c2=cross(a2-a1,b2-a1),c3=cross(b2-b1,a1-b1),c4=cross(b2-b1,a2-b1);return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0;
}
至少到这里为止的计算几何是不需要图片作为补充的,然而下面我们就需要了。
当然,这里需要先给出通过计算求近似折线的算法(也不知道第几版代码了):
vector<pair<point,point>> aprlin[3];
void approx(int num){double st=1/ROX;vector<point> aprdot;for(double i=0;i*st<1;i++) aprdot.push_back(curv[num].C(st*i));for(int i=1;i<aprdot.size();i++) aprlin[num].push_back(make_pair(aprdot[i-1],aprdot[i]));
}
而后,我们就要求折线的全部交点了——这就是我们的任务。
首先上场的是 O(n2)\mathrm O(n^2)O(n2) 的暴力判断,这哥们把所有的线段两两互相判断,代码如下:
vector<point> ans,shans;
for(auto it:aprlin[1]) for(auto jt:aprlin[2]){if(isintersected(it.first,it.second,jt.first,jt.second)){point pi=getintersection(it.first,it.second-it.first,jt.first,jt.second-jt.first);ans.push_back(pi);}
}
这里的 shans 是为了精度和去重用的,暂且不需要它。
然而不幸的是,如果你使用如上的代码,你会 TLE。怎么办?我们需要更快的算法求任意两条线段的交点(当然,如果两条线段不分属两个集合,我们可以特判)。
在多方查找后,我在这里找到了一个好的算法,在这里叙述一下。
这个算法是扫描线的另一种奇妙的实现。算法要求我们首先开一个链表,用以保存所有的线段端点以及找到的交点,按照 yyy 坐标从大到小,xxx 坐标从小到大的递增顺序建立链表;以及一棵二叉查找树,记录与扫描线相交的线段的编号,按照所在线段的上端点的 xxx 坐标递增顺序存储。
在这里我采用的实现方式是指针链表和 set 实现的二叉查找树(Treap,Splay 太烦了不想写),当然用自定义的 cmp 来排列元素,因此代码是这样写的:
struct cmp{bool operator()(int a,int b){point at,bt;if(aprlin[a].first.p1.y<aprlin[a].first.p2.y) at=aprlin[a].first.p2;else at=aprlin[a].first.p1;if(aprlin[b].first.p1.y<aprlin[b].first.p2.y) bt=aprlin[b].first.p2;else bt=aprlin[b].first.p1;return at.x<bt.x;}
};
set<int,cmp> bst;
我们还得探究一下,如何保留点所在线段的信息(交点需要两个!),点的类型(分为上点、下点和交点,字面意思,与扫描线平行的强行区分),以及它们之间的比较,因此我又定义了个结构体 endpoint 用来记录它(下面的 node 是链表节点,不论):
const int BOTTOM=0,TOP=1,INTERSECT=-1;
struct endpoint{point p;int seg,ges,st;endpoint(point p=point(0,0),int seg=0,int ges=0,int st=0):p(p),seg(seg),ges(ges),st(st){}
};
struct node{endpoint ep;node *next;node(endpoint ep=endpoint(),node *next=nullptr):ep(ep),next(next){}
}*head;
那么初始化这条链表的代码如下(一开始我们存了所有线段的端点):
vector<endpoint> edps;
int n=aprlin.size();
for(int i=0;i<n;i++){if(aprlin[i].first.p1.y>aprlin[i].first.p2.y){edps.push_back(endpoint(aprlin[i].first.p1,i,0,TOP));edps.push_back(endpoint(aprlin[i].first.p2,i,0,BOTTOM));}else{edps.push_back(endpoint(aprlin[i].first.p1,i,0,BOTTOM));edps.push_back(endpoint(aprlin[i].first.p2,i,0,TOP));}
}
sort(edps.begin(),edps.end(),[](endpoint a,endpoint b)->bool {return a.p.y!=b.p.y?a.p.y>b.p.y:a.p.x<b.p.x;});
head=new node;
node *cur=head,*co=head;
for(int i=0;i<2*n;i++){cur->ep=edps[i];if(cur->next==nullptr) cur->next=new node;co=cur,cur=cur->next;
}
delete cur,co->next=nullptr;
cur=head;
下面的过程非常之恐怖,因此略去代码,专门讲解几何部分。
扫描线按照链表行进,可能会遇到如下的三种情况:
- 扫描线碰上了某条线段的上点。这时我们设该线段编号为 it\mathfrak{it}it,左边线段为 lt\mathfrak{lt}lt,右边线段为 rt\mathfrak{rt}rt,左边线段 lt\mathfrak{lt}lt 和右边线段 rt\mathfrak{rt}rt 指在二叉查找树中与 it\mathfrak{it}it 相邻的两条线段,那么如图所示:
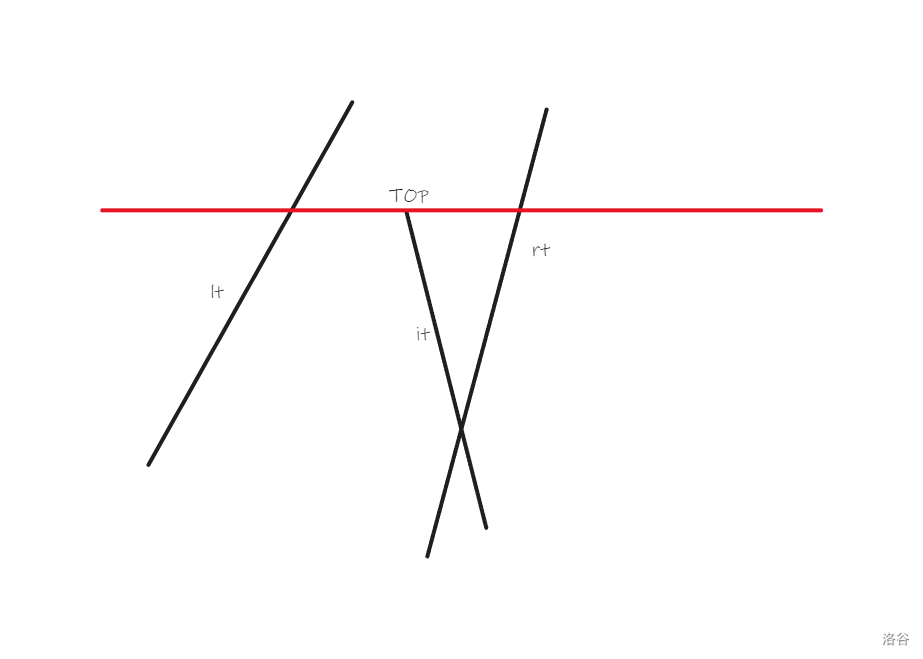 我们就可以把 it\mathfrak{it}it 塞进二叉查找树,而后判断 it\mathfrak{it}it 和 lt\mathfrak{lt}lt 以及 rt\mathfrak{rt}rt 是否相交。相交的节点一定在扫描线的下方(因为如果它在上方,说明我们已经搜索到了它并且已经用它插入过线段了),而后我们就把交点插入链表。
我们就可以把 it\mathfrak{it}it 塞进二叉查找树,而后判断 it\mathfrak{it}it 和 lt\mathfrak{lt}lt 以及 rt\mathfrak{rt}rt 是否相交。相交的节点一定在扫描线的下方(因为如果它在上方,说明我们已经搜索到了它并且已经用它插入过线段了),而后我们就把交点插入链表。 - 扫描线碰到了某条线段的下点,设的同上,我们就有
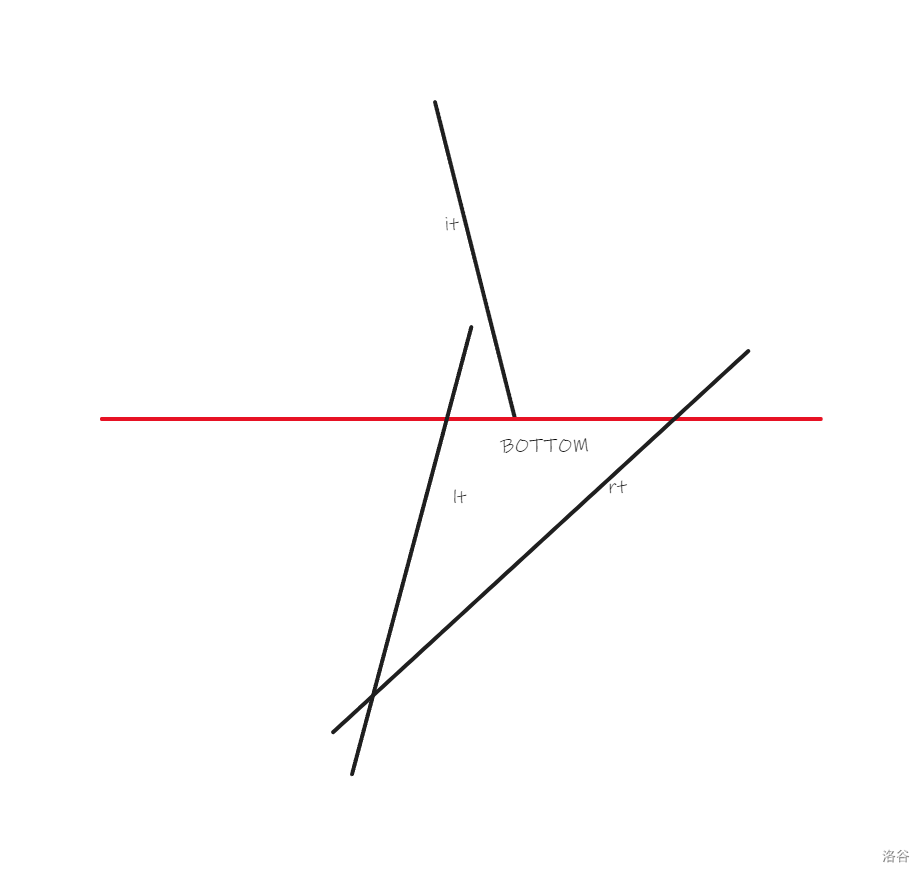 这时我们把 lt\mathfrak{lt}lt 和 rt\mathfrak{rt}rt 判断一下是否相交,如果相交就把交点插入链表,而后把 it\mathfrak{it}it 从扫描线中删除。当然,交点还是在扫描线的下方。
这时我们把 lt\mathfrak{lt}lt 和 rt\mathfrak{rt}rt 判断一下是否相交,如果相交就把交点插入链表,而后把 it\mathfrak{it}it 从扫描线中删除。当然,交点还是在扫描线的下方。 - 扫描线碰到了两条线段的交点,这时我们设这两条相交的线段编号分别为 it\mathfrak{it}it 和 jt\mathfrak{jt}jt(这里 it\mathfrak{it}it 在二叉查找树中相对于 jt\mathfrak{jt}jt 是在左边的!),并且设 it\mathfrak{it}it 的左相邻线段为 lt\mathfrak{lt}lt,jt\mathfrak{jt}jt 的右相邻线段为 rt\mathfrak{rt}rt,如图所示:
 我们只需要判定 it\mathfrak{it}it 和 rt\mathfrak{rt}rt 是否相交以及 lt\mathfrak{lt}lt 和 jt\mathfrak{jt}jt 是否相交,而其他的交点我们已经找过了。
我们只需要判定 it\mathfrak{it}it 和 rt\mathfrak{rt}rt 是否相交以及 lt\mathfrak{lt}lt 和 jt\mathfrak{jt}jt 是否相交,而其他的交点我们已经找过了。
当然,这里需要注意的是,由于采用的是 set 来实现二叉查找树,所以它的 iterator 中寻找该元素要用 lower_bound,它的左邻居需要先判断是否是 begin() 而后左移,右邻居需要先右移而后判断是不是 end(),因为 end() 指向最后一个元素的后一个元素。最后释放整个链表。
本题完整版代码如下(为防止抄袭,RRR 和 ϵ\epsilonϵ 的数值更改):
#include <iostream>
#include <cmath>
#include <iomanip>
#include <set>
#include <algorithm>
#include <vector>
#include <map>
#define fs(X) fixed<<setprecision(X)
using namespace std;
const double EPS=0,ROX=0;
int dcmp(double x){if(fabs(x)<EPS) return 0;else return x<0?-1:1;
}
struct point{double x,y;point(double cx=0,double cy=0):x(cx),y(cy){}point operator+(point b){return point(x+b.x,y+b.y);}point operator-(point b){return point(x-b.x,y-b.y);}point operator*(double cof){return point(x*cof,y*cof);}point operator/(double b){double xx=x/b,yy=y/b;if(dcmp(x)==0||dcmp(b)==0) xx=0;if(dcmp(y)==0||dcmp(b)==0) yy=0;return point(xx,yy);}
};
typedef point vecto;
double cross(vecto a,vecto b){return a.x*b.y-a.y*b.x;
}
struct segment{point p1,p2;segment(point p1,point p2):p1(p1),p2(p2){}
};
bool isintersected(point a1,point a2,point b1,point b2){double c1=cross(a2-a1,b1-a1),c2=cross(a2-a1,b2-a1),c3=cross(b2-b1,a1-b1),c4=cross(b2-b1,a2-b1);return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0;
}
point getintersection(point p,vecto v,point q,vecto w){vecto u=p-q;double t=cross(w,u)/cross(v,w);return p+v*t;
}
struct nurbs{int n,k,m;point P[25];double w[25],t[25];double N(int i,int k,double u){if(k==0) return (t[i]<=u&&u<t[i+1]?1.0:0.0);double co0,co1;if(dcmp(t[i+k]-t[i])==0||dcmp(u-t[i])==0) co0=0;else co0=(u-t[i])/(t[i+k]-t[i]);if(dcmp(t[i+k+1]-u)==0||dcmp(t[i+k+1]-t[i+1])==0) co1=0;else co1=(t[i+k+1]-u)/(t[i+k+1]-t[i+1]);return co0*N(i,k-1,u)+co1*N(i+1,k-1,u);}point C(double u){point num=point(0,0);double dem=0;for(int i=1;i<=n;i++){double coef=w[i]*N(i,k,u);num=num+P[i]*coef;dem+=coef;}return num/dem;}void clear(){n=k=m=0;for(int i=0;i<25;i++) P[i].x=P[i].y=w[i]=t[i]=0;}
}curv[3];
vector<pair<segment,int>> aprlin;
const int BOTTOM=0,TOP=1,INTERSECT=-1;
struct endpoint{point p;int seg,ges,st;endpoint(point p=point(0,0),int seg=0,int ges=0,int st=0):p(p),seg(seg),ges(ges),st(st){}
};
struct node{endpoint ep;node *next;node(endpoint ep=endpoint(),node *next=nullptr):ep(ep),next(next){}
}*head;
void approx(int num){double st=1/ROX;vector<point> aprdot;for(double i=0;i*st<1;i++) aprdot.push_back(curv[num].C(st*i));for(int i=1;i<aprdot.size();i++) aprlin.push_back(make_pair(segment(aprdot[i-1],aprdot[i]),num));
}
void intersections(vector<point> &ans){vector<endpoint> edps;int n=aprlin.size();for(int i=0;i<n;i++){if(aprlin[i].first.p1.y>aprlin[i].first.p2.y){edps.push_back(endpoint(aprlin[i].first.p1,i,0,TOP));edps.push_back(endpoint(aprlin[i].first.p2,i,0,BOTTOM));}else{edps.push_back(endpoint(aprlin[i].first.p1,i,0,BOTTOM));edps.push_back(endpoint(aprlin[i].first.p2,i,0,TOP));}}sort(edps.begin(),edps.end(),[](endpoint a,endpoint b)->bool {return a.p.y!=b.p.y?a.p.y>b.p.y:a.p.x<b.p.x;});head=new node;node *cur=head,*co=head;for(int i=0;i<2*n;i++){cur->ep=edps[i];if(cur->next==nullptr) cur->next=new node;co=cur,cur=cur->next;}delete cur,co->next=nullptr;cur=head;struct cmp{bool operator()(int a,int b){point at,bt;if(aprlin[a].first.p1.y<aprlin[a].first.p2.y) at=aprlin[a].first.p2;else at=aprlin[a].first.p1;if(aprlin[b].first.p1.y<aprlin[b].first.p2.y) bt=aprlin[b].first.p2;else bt=aprlin[b].first.p1;return at.x<bt.x;}};set<int,cmp> bst;while(cur!=nullptr){if(cur->ep.st==TOP){bst.insert(cur->ep.seg);auto it=bst.lower_bound(cur->ep.seg),lt=it,rt=it;rt++;if(rt!=bst.end()){if(isintersected(aprlin[*it].first.p1,aprlin[*it].first.p2,aprlin[*rt].first.p1,aprlin[*rt].first.p2)){point pi=getintersection(aprlin[*it].first.p1,aprlin[*it].first.p2-aprlin[*it].first.p1,aprlin[*rt].first.p1,aprlin[*rt].first.p2-aprlin[*rt].first.p1);node *nx=cur->next,*add=new node;add->ep=endpoint(pi,*it,*rt,INTERSECT);add->next=nx,cur->next=add;}}if(lt!=bst.begin()){lt--;if(isintersected(aprlin[*it].first.p1,aprlin[*it].first.p2,aprlin[*lt].first.p1,aprlin[*lt].first.p2)){point pi=getintersection(aprlin[*it].first.p1,aprlin[*it].first.p2-aprlin[*it].first.p1,aprlin[*lt].first.p1,aprlin[*lt].first.p2-aprlin[*lt].first.p1);node *nx=cur->next,*add=new node;add->ep=endpoint(pi,*lt,*it,INTERSECT);add->next=nx,cur->next=add;}}}else if(cur->ep.st==BOTTOM){auto it=bst.lower_bound(cur->ep.seg),lt=it,rt=it;++rt;if(lt!=bst.begin()&&rt!=bst.end()){lt--;if(isintersected(aprlin[*rt].first.p1,aprlin[*rt].first.p2,aprlin[*lt].first.p1,aprlin[*lt].first.p2)){point pi=getintersection(aprlin[*rt].first.p1,aprlin[*rt].first.p2-aprlin[*rt].first.p1,aprlin[*lt].first.p1,aprlin[*lt].first.p2-aprlin[*lt].first.p1);node *nx=cur->next,*add=new node;add->ep=endpoint(pi,*lt,*rt,INTERSECT);add->next=nx,cur->next=add;}}bst.erase(cur->ep.seg);}else if(cur->ep.st==INTERSECT){if(aprlin[cur->ep.seg].second+aprlin[cur->ep.ges].second==3) ans.push_back(cur->ep.p);auto it=bst.lower_bound(cur->ep.seg),jt=bst.lower_bound(cur->ep.ges);auto lt=it,rt=jt;++rt;if(rt!=bst.end()){if(isintersected(aprlin[*jt].first.p1,aprlin[*jt].first.p2,aprlin[*rt].first.p1,aprlin[*rt].first.p2)){point pi=getintersection(aprlin[*jt].first.p1,aprlin[*jt].first.p2-aprlin[*jt].first.p1,aprlin[*rt].first.p1,aprlin[*rt].first.p2-aprlin[*rt].first.p1);node *nx=cur->next,*add=new node;add->ep=endpoint(pi,*jt,*rt,INTERSECT);add->next=nx,cur->next=add;}}if(lt!=bst.begin()){lt--;if(isintersected(aprlin[*lt].first.p1,aprlin[*lt].first.p2,aprlin[*it].first.p1,aprlin[*it].first.p2)){point pi=getintersection(aprlin[*lt].first.p1,aprlin[*lt].first.p2-aprlin[*lt].first.p1,aprlin[*it].first.p1,aprlin[*it].first.p2-aprlin[*it].first.p1);node *nx=cur->next,*add=new node;add->ep=endpoint(pi,*lt,*it,INTERSECT);add->next=nx,cur->next=add;}}}cur=cur->next;}cur=head;do{node *co=cur->next;delete cur;cur=co;}while(cur!=nullptr);
}
int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int T;cin>>T;for(int tid=1;tid<=T;tid++){if(tid>1) cout<<endl;aprlin.clear();for(int i=1;i<=2;i++) curv[i].clear();for(int i=1;i<=2;i++){cin>>curv[i].n>>curv[i].m,curv[i].k=curv[i].m-curv[i].n-1;for(int j=1;j<=curv[i].n;j++) cin>>curv[i].P[j].x>>curv[i].P[j].y>>curv[i].w[j];for(int j=1;j<=curv[i].m;j++) cin>>curv[i].t[j];approx(i);}vector<point> ans;intersections(ans);cout<<"Case "<<tid<<": ";if(ans.empty()){cout<<0<<endl;continue;}sort(ans.begin(),ans.end(),[](point a,point b)->bool {return a.x!=b.x?a.x<b.x:a.y<b.y;});cout<<ans.size()<<endl;for(auto it:ans) cout<<"("<<fs(3)<<it.x<<", "<<fs(3)<<it.y<<")"<<endl;}return 0;
}
真的好长。当然,对于交点,我们可以在特判后(采用在双向广搜中使用的技巧,编号和为 333)把答案压入 vector 而后排序。
写这道题是为了计算几何入门的,结果一不小心就变成了这样:

可能前两个还是较为有趣的,但是第三个就有些恐怖了——自 2012 年出的题目,竟然到现在 A 掉它的不超过 555 个人!
好吧,最后贡献一组 Hack(从比赛的官方文件中薅下来的)。
EOF
相关文章:

可爱的魔法曲线 Lovely Magical Curves(12年开始只有5个人AC)
一起来交流编程吧!【CSDN app】:http://qm.qq.com/cgi-bin/qm/qr?_wv1027&k3svdDJTlkD76TRRShbxYCYK1zK1c8cyF&authKeyv1pxp6rS8AA4SRy7bflJl9LIwp8d5v0HOudw%2BDxHiWDRqZ1LzjeoBJH1Z1EXnl35&noverify0&group_code546881376 可爱的魔法…...

通过C++程序实现光驱的自动化刻录和读取
文章目录 ISO文件格式光盘的基本概念光盘种类特点DVDR光盘使用windows调用Linux调用Linux平台下用到的C库:读取设备驱动列表向光驱中写文件 数字存储媒体快速发展的今天,光驱的使用已经不像以前那样普及了。但是在数据备份、安装软件和操作系统、旧设备兼容等领域还…...

【电商项目实战】商品详情显示与Redis存储购物车信息
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《电商项目实战》。🎯🎯 &am…...

概率论基础
1.概率论 1.1 随机事件与概率 1.1.1 基本概念 样本点(sample point): 称为试验 S S S的可能结果为样本点,用 ω \omega ω表示。 样本空间(sample space):称试验 S S S的样本点构成的集合为样本空间,用 Ω \Omega Ω表示…...

Mac电脑CMake安装和配置
1.从CMake官网下载dmg文件并且安装 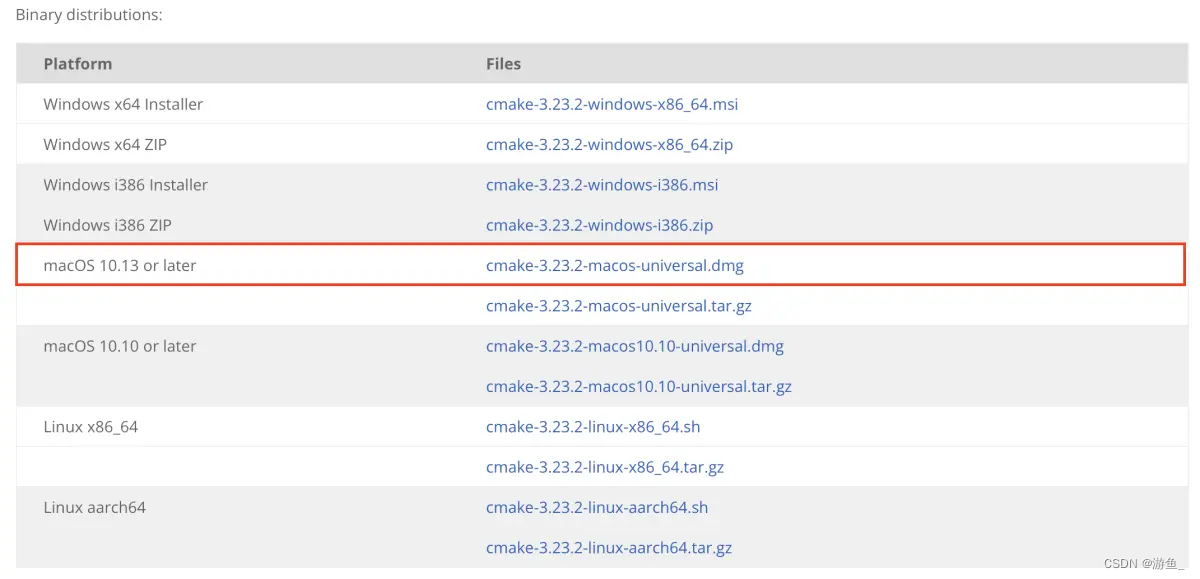...

FormData传送复杂数据
FormData 是一个用于创建表单数据对象的 JavaScript 类。它通常用于通过 JavaScript 发送表单数据,尤其是用于发送 AJAX 请求时非常有用。 使用 FormData 可以方便地构建一个以 multipart/form-data 格式提交的表单数据,这允许你在发送 XMLHttpRequest …...

力扣回溯算法-电话号码的字母组合
力扣第17题,电话号码的字母组合 题目 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 .电话号码的字母组合 示例: 输入:“2…...

运维面试笔试题
目录 shell脚本 nginx 数据库mysql k8s(kubernetes) 安全与防护 网络TCP/IP shell脚本 1 通过正则表达式匹配文本...

Oracle database 静默安装 oracle12c 一键安装 12.1.0.2
基于oracle安装包中应答文件实现一键安装 注意此安装脚本基于12.1.0.2 安装包 原始安装包结构为两个压缩包 此脚本使用安装包为原始压缩包解压后、 重新封装为一个.zip压缩包 建议在linux 环境下解压重新压缩后 使用该脚本 支持环境: Linux :centerOS 7 oracle :12.1.0.…...

【Java EE初阶三 】线程的状态与安全(上)
1. join方法与多线程 1.1 初识多线程 为了提高cpu得利用率,因此就引入了多个线程的概念;即每个线程负责完成整个程序的一部分工作即可。 写一个代码,让主线程,创建一个新的线程,由新线程负责完成运算(12。…...
如何实现GTM与DSADC关联的配置)
英飞凌TC3xx之一起认识GTM系列(五)如何实现GTM与DSADC关联的配置
英飞凌TC3xx之一起认识GTM系列(五)如何实现GTM与DSADC关联的配置 1 GTM与DSADC的连接1.1 EDSADC 到 GTM 的连接1.1.1 工作原理说明1.1.2 应用举例1.2 GTM 到 EDSADC 的连接1.2.1 工作原理说明1.2.2 应用举例2 总结编者按:笔者在从事这部分开发工作的时候,看着手册上的各种通…...
小兔鲜儿 uniapp - 购物车模块
目录 加入购物车 接口相关 购物车列表 静态结构 登录状态 列表渲染 删除购物车 接口相关 参考代码 修改商品信息 接口相关 修改商品数量 修改商品选中/全选 底部结算信息 计算总钱数(总金额) 带返回按钮的购物车 完成加入购物车…...

Python使用PyMySql增删改查Mysql数据库
PyMysql简介 PyMysql是Python中用于连接MySQL数据库的一个第三方库,它实现了MySQL客户端/服务器协议,使得Python程序能够与MySQL服务器进行交互。由于Python 2的mysql-python(又称mysqldb)模块在Python 3上支持不够完善࿰…...
前端实现websocket类封装
随着Web应用程序的发展,越来越多的人开始利用Websocket技术来构建实时应用程序。Websocket是一种在客户端和服务器之间建立持久连接的协议。这种协议可以在一个单独的连接上实现双向通信。与HTTP请求-响应模型不同,Websocket允许服务器自主地向客户端发送…...
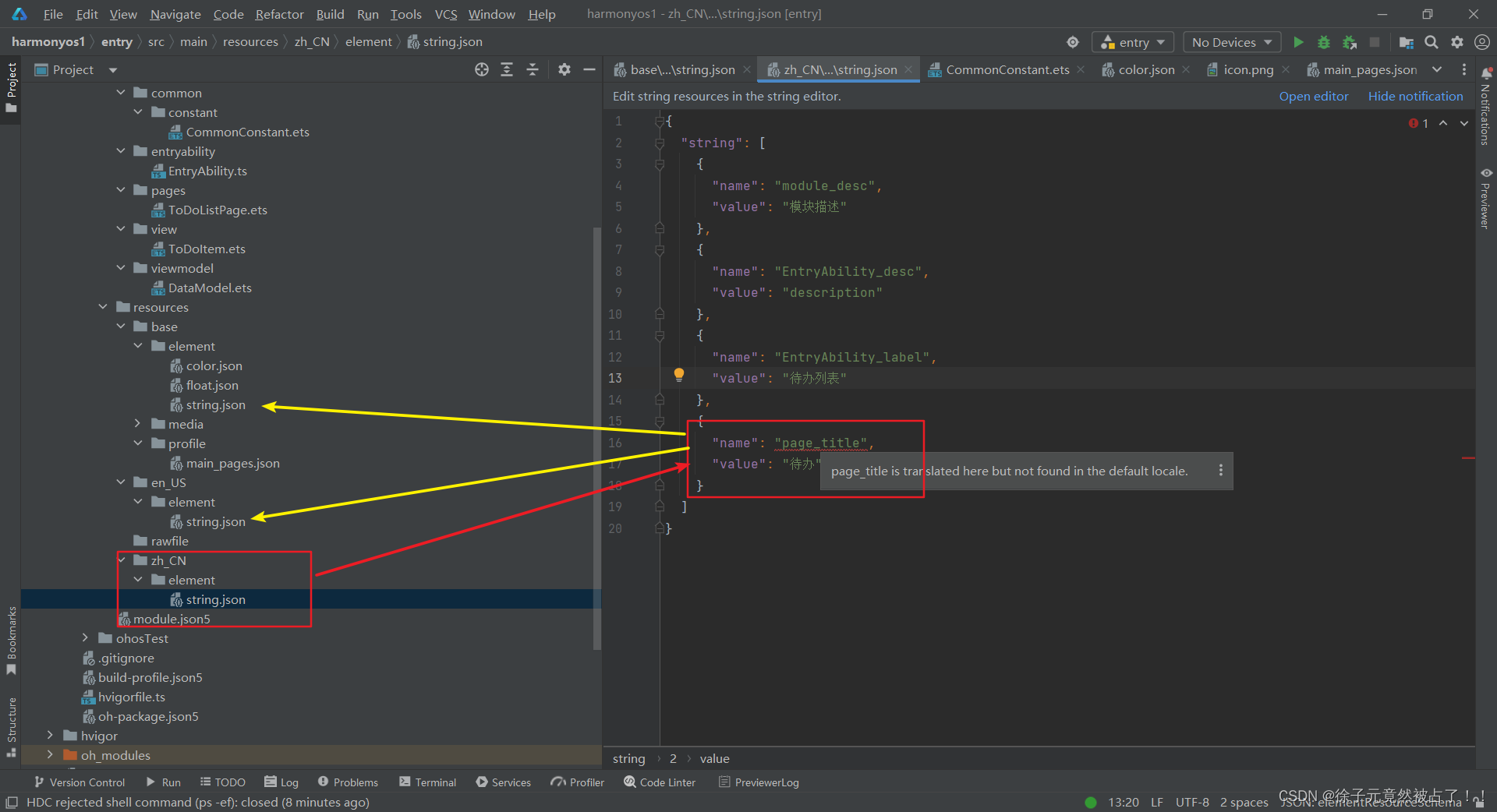
鸿蒙开发中的一些小问题
这是我在学习鸿蒙开发中遇见的小问题 Q1:This custom component must have a build function. <etsLint>Q2:page_title is not translated into en_US(American English)Q3:Module "../CustomComponent/CustomButton" declar…...

OpenCV-12绘制图像
OpenCV提供了许多绘制图像的API,可以在图像上绘制各种图形,例如直线,矩形,圆,椭圆等图形。 一、画直线 利用API line(img, pt1, pt2, color, thickness, lineType, shift)可以绘制直线。 其中…...

“2023年的技术发展与个人成长:回顾与展望“
文章目录 每日一句正能量前言工作生活未来展望后记 每日一句正能量 凡事顺其自然,遇事处于泰然,得意之时淡然,失意之时坦然,艰辛曲折必然,历尽沧桑悟然。 前言 在这快速发展的信息时代,技术的进步和创新不…...
算法逆袭之路(1)
11.29 开始跟进算法题进度! 每天刷4题左右 ,一周之内一定要是统一类型 而且一定稍作总结, 了解他们的内在思路究竟是怎样的!! 12.24 一定要每天早中晚都要复习一下 早中午每段一两道, 而且一定要是同一个类型, 不然刷起来都没有意义 12.26/27: 斐波那契数 爬…...

2023.12.31每日一题
LeetCode每日一题 2023年的最后一题 1154.一年中的第几天 1154. 一年中的第几天 - 力扣(LeetCode) 描述 给你一个字符串 date ,按 YYYY-MM-DD 格式表示一个 现行公元纪年法 日期。返回该日期是当年的第几天。 示例 1: 输入&a…...
)
Flink实时电商数仓(八)
用户域登录各窗口汇总表 主要任务:从kafka页面日志主题读取数据,统计 七日回流用户:之前活跃的用户,有一段时间不活跃了,之后又开始活跃,称为回流用户当日独立用户数:同一个用户当天重复登录&a…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...
