算法逆袭之路(1)
11.29
开始跟进算法题进度!
每天刷4题左右 ,一周之内一定要是统一类型
而且一定稍作总结, 了解他们的内在思路究竟是怎样的!!
12.24
一定要每天早中晚都要复习一下
早中午每段一两道, 而且一定要是同一个类型, 不然刷起来都没有意义
12.26/27:
斐波那契数
爬楼梯
最小花费爬楼梯
不同路径1/2
12.28:
整数拆分

重点思路:一个正整数可以分为两个,或者多个,多个可以用dp[i-j]代替,一定不能直接分为乘以dp的情况,因为这就默认了必须拆分为三个以上
不同的二叉搜索树
重点思路: 把左右子树所有情况乘起来,递归子树的问题。注意左右节点个数的边界
12.29
01背包理论
12.30
分割等和子集

很难看出来是01背包。满足的条件有
-
每个元素只有取和不取两个状态
-
结果要满足,某一部分和,刚好等于什么什么value,而背包问题是在限制的重量内计算他们价值最大值, 这里只需把求最大值改成求刚好 == sum即可
-
此题的weight和value都是nums【i】,因为是一个一个数字要求刚好和为sum
-
dp【i】代表在i内之和最大为多少 本题要求刚好等于sum所以结束条件是dp[ sum ] == sum ,即总量为sum之内刚好最大为sum!
581. 最短无序连续子数组
12.31
-
209. 长度最小的子数组

思路:滑动窗口,先不断右移直到sum>=target , 然后左指针左移直到小于target,记录暂时的最小长度,然后继续右移右移直到sum>=target , 左指针左移直到小于target,不断迭代最小长度
-
和为 K 的子数组

使用前缀和,核心是
map.containskey(sum-k); map.put(sum,map.getOrDefault(sum,0)+1);
滑动窗口
按照这题为模板
这种题的特征是 "子串" "子数组" 这种需要连续元素的
有一个窗口在扫描,使用两个变量left限制左范围:right用于for遍历计数
tmp,max用于记录最终数据
从0处开始滑动区间 ,right每加一次,就判断right这个元素和窗口内的元素是否满足某种条件
如果不满足了就进入处理块, 不断把left向右推进直到他满足条件, 在外层循环记录tmp和最大的max即可.(此题判断的条件是是否有重复元素,有就把left推进到重复的位置)
无重复字符最长子串
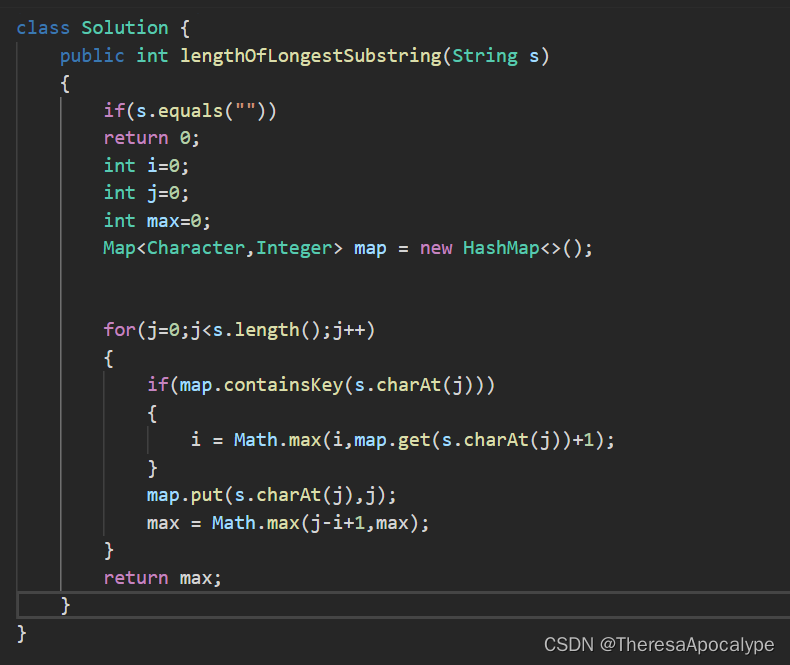
字节最经典的一道题
注意要用HashMap提高查找效率
-
containsKey先于put处理防止自己contains自己。调整i位置,通过比较两个元素下标谁大,来确定谁是后面的0
-
左边界调整位置的时候调整到第一个有效位(即重复位+1),而不是重复位,因为如果这个字符串没有重复的,此时应该使用j-i+1计算结果, 然而如果是调整到重复位 结果就变成了j-i,没有统一。所以必须挪到重复位的右边(第一个有效位)!
-
i = Math.max(i,map.get(s.charAt(j))+1); 这一句是比较 当前边界和重复字符谁更右 ,
取更右边的作为边界
重点:要用HashMap来搞。注意put是会覆盖相同的元素的!!!!由于遍历的顺序是下标由小到大,因此得到的那个重复元素的下标一定是目前最大的,直接和左边界比较即可
哈希表(12.9-12.16)
什么时候使用哈希法:
1.当我们需要查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法。
经典题: 比较两个集合的元素重叠的地方, 或者这个数组能不能由那个数组里的元素构成
2.当我们需要在一次遍历中记录某种元素出现的次数, 或者记录某个和他相关的特征的时候
抽象来说就是, 需要建立一个数据和另一个数据之间的映射关系的时候
下面是这两种数据结构的一些常用方法:
HashMap
-
put(key, value): 如果key已经存在,那么值就更新 -
get(key): 根据key获取value -
remove(key): 删除HashMap中指定key的元素 -
containsKey(key): 检查HashMap中是否包含给定的key -
containsValue(value): 检查HashMap中是否包含给定的value -
keySet(): 返回所有key的Set -
values(): 返回所有value的Collection -
isEmpty(): 检查是否为空 -
clear(): 清除所有元素 -
map.put(i , getOrDefault(map.get(i),0)+1)
HashSet
-
add(element): 添加一个元素 -
remove(element): 删除一个元素 -
contains(element):是否包含给定的元素 -
isEmpty(): 检查是否为空 -
clear(): 清除所有元素 -
size(): 返回元素的数量 -
iterator(): 返回一个迭代器,用于遍历HashSet中的所有元素。
回溯(12.19-12.24)
为什么要用回溯?
-
for循环只能有单层遍历,但是回溯是可以多层遍历
-
回溯的本质就是多层遍历, 用for循环控制这一层的广度, 用递归控制深度, 用退出条件控制结束时机
-
一定要画图辅助理解,可以明确写递归方法的思路, 这很重要
-
什么题用回溯?问你返回所有可能得什么什么组合,集合, 需要枚举/遍历所有情况 , 特别是组合/子集问题,要从题目抽象中出来
基本步骤
-
定义结果res集合(ArrayList) 临时存储tmp集合(LinkedList) 当前总和int sum
List<List<Integer>> res = new ArrayList<>();List<Integer> tmp = new LinkedList<>();int sum=0;
-
定义dfs函数, 包含传入的数组nums, 每次遍历的开头begin, 目标target
-
定义退出条件: 等于target时 把tmp加入res然后返回 超出target直接返回 大小超出也返回
-
定义循环体:注意for(i=begin;i<length;i++)
-
tmp.add(candidates[i]);sum += candidates[i];dfs(candidates, i ,target);sum -= candidates[i];tmp.removeLast();
三大要点总结
-
数组中(有无)重复元素
-
结果中(能否)含有重复元素
-
结果(能否)出现重复集合(顺序不同是否算同一个集合)
主要是修改i = begin参数 和 dfs(nums, i ,target)中是 i 还是 i+1
子集能重复, 只用修改为 i=0 不可重复则是 i=begin
重点情况:
-
数组中无重复元素 结果中不能含有重复元素 子集不能出现重复:
i=begin dfs(nums, i+1 ,target)
-
数组中有重复元素 结果中能含有重复元素 子集不能出现重复:
加条件:
if(i > begin && nums[i] == nums[i-1]) continue;
i=begin dfs(nums, i+1 ,target)
-
数组中有重复元素 结果中不含有重复元素 子集不能出现重复:
加条件:
if(i > 0 && nums[i] == nums[i-1]) continue;
i=begin dfs(nums, i+1 ,target)
###
回文子串问题
12.28
class Solution {List<List<String>> res = new ArrayList<>();List<String> tmp = new LinkedList<>();public List<List<String>> partition(String s) {int index = 0;dfs(0,s);return res;}
public void dfs(int index , String s){if(index == s.length()){res.add(new ArrayList(tmp));}
for(int i = index;i < s.length();i++){if(fun(index,i,s) == true) {String now = s.substring(index,i+1);tmp.add(now);dfs(i+1,s);tmp.removeLast();}}}
public boolean fun(int i,int j,String s){while(true){if(i >= j)return true;if(s.charAt(i) != s.charAt(j)){return false;}i++;j--;}}
}
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
可以算困难一级的了
难点:
-
把分割方案化为回溯问题, 我们想枚举每一种字符串的分割方式, 再一个一个去验证
-
可以看做是字符间空隙的组合问题(在一个空隙集合中选择不同的空隙组合) 采用回溯枚举
-
因为for循环只能有单层遍历,但是回溯是可以多层遍历(回溯的本质就是遍历, 用for循环控制这一层的广度, 用递归控制深度, 用退出条件控制结束时机 )
-
一定要画图辅助理解, 这很重要,一开始都没意识到
-
判断回文直接双指针
-
//我们使用index来代表当前遍历的空隙, 当枚举到**最后一个字符后**的空隙时就才遍历 if(index == s.length()) {res.add(new ArrayList(tmp));} for(int i = index;i < s.length();i++){//index和i表示我们当前处理的哪两个空隙之间的字符串,只有当前满足是回文我们才继续去dfs,否则直接进入下一个循环,这样保证了只有回文, 并且因为只有遍历到最后一个字符后才会结束,所以不用担心会脏结果if(fun(index,i,s) == true) {String now = s.substring(index,i+1); //注意边界是[index,i]tmp.add(now);dfs(i+1,s);//从下一个字符开始继续判断tmp.removeLast();}}
动态规划(12.25-1.4)
如果某一问题有很多重叠子问题,使用动态规划是最有效的。
就是你发现这一步的答案要根据上一步的答案得,而且上一步的答案也是同样的方法得到的
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的
状态转移公式(递推公式)是很重要,但动规不仅仅只有递推公式。
动规五步曲(一定要明确的每一步结果写出来)
-
确定dp数组(dp table)以及下标的含义
这很重要,注释出来
-
确定递推公式
写完dp数组含义以后 立马着手递推公式 用注释先写上
-
dp数组如何初始化
一定要注意dp[0] dp[1] 这种边界值的初始化,很有可能要取特值
-
确定遍历顺序
要确保后面的可以由前面的推出来,特别是多维dp
-
举例推导dp数组
为什么要先确定递推公式,然后在考虑初始化呢?因为一些情况是递推公式决定了dp数组要如何初始化!
Debug三问
-
这道题目我举例推导状态转移公式了么?
-
我打印dp数组的日志了么?
-
打印出来了dp数组和我想的一样么?
背包问题
01背包
(1)
对于背包问题,有一种写法即dpi 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
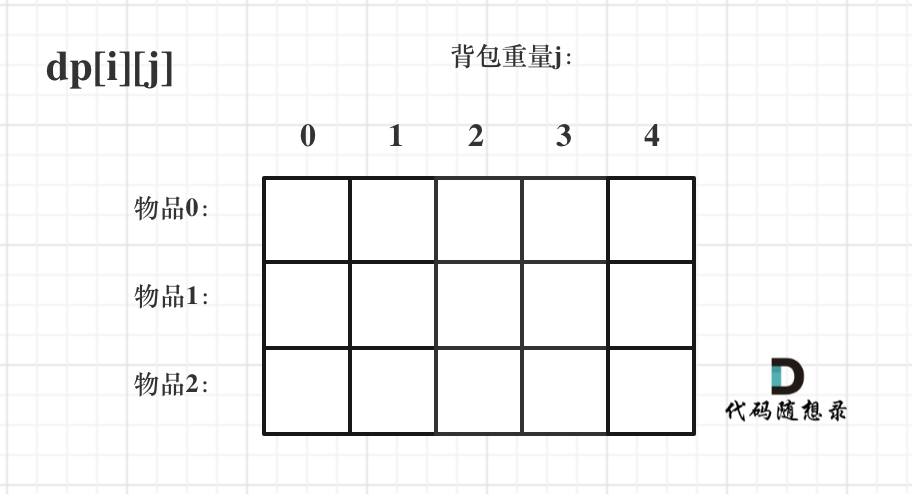
确定递推公式
不放物品i:和上一个相同。由dp[i - 1] [j]推出,即背包容量为j,里面不放物品i的最大价值,此时dpi就是dp[i - 1] [j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
放物品i:等于上一个加这个的value。由dp[i - 1] [j - weight[i]]推出,dp[i - 1] [j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1] [j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
取i那就是后者,不取i就是前者
dp[i][j] = max{ dp[i-1][j] , dp[i-1][j-weight[i]] + value[i] }
(2)滚动数组法
重点一定要记住, 就是数据的覆盖
在此时,数组是一遍一遍覆盖的。覆盖前就相当于原来的dp[i-1 ] [j ],所以此时,不取物品i 的情况就可以化为dp[j ] 直接就是上一个的。同理,要取物品i 就直接化为dp[j-weight ]+value[j ]
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]
初始化dp就应该全是0,在题目给的全是正整数的情况下可以保证后续被覆盖掉。
循环还是双重循环,要有i 控制前n个物品进不进去, 但是dp会减少一维度
同时我们可以窥见遍历的次序问题。因为我们要保证j 之前的数据还没有被覆盖
因为有比较dp[j - weight[i]] + value[i]的部分
所以我们要倒序遍历
ps:能不能交换遍历顺序?不能,不然就变成 dp[j]表示:取前 j 个的背包,所背的物品价值可以最大为dp[j]
相关文章:

算法逆袭之路(1)
11.29 开始跟进算法题进度! 每天刷4题左右 ,一周之内一定要是统一类型 而且一定稍作总结, 了解他们的内在思路究竟是怎样的!! 12.24 一定要每天早中晚都要复习一下 早中午每段一两道, 而且一定要是同一个类型, 不然刷起来都没有意义 12.26/27: 斐波那契数 爬…...

2023.12.31每日一题
LeetCode每日一题 2023年的最后一题 1154.一年中的第几天 1154. 一年中的第几天 - 力扣(LeetCode) 描述 给你一个字符串 date ,按 YYYY-MM-DD 格式表示一个 现行公元纪年法 日期。返回该日期是当年的第几天。 示例 1: 输入&a…...
)
Flink实时电商数仓(八)
用户域登录各窗口汇总表 主要任务:从kafka页面日志主题读取数据,统计 七日回流用户:之前活跃的用户,有一段时间不活跃了,之后又开始活跃,称为回流用户当日独立用户数:同一个用户当天重复登录&a…...

Python Pymysql实现数据存储
什么是 PyMySQL? PyMySQL 是在 Python3.x 版本中用于连接 MySQL 服务器的一个库,Python2 中则使用mysqldb。 PyMySQL 遵循 Python 数据库 API v2.0 规范,并包含了 pure-Python MySQL 客户端库。 PyMySQL 安装 在使用 PyMySQL 之前…...

软件测试/测试开发丨Python 常用第三方库 pymysql
pymysql 概述 Python 的数据库接口标准是 Python DB-APIPyMySQL 是从 Python 连接到 MySQL 数据库服务器的接口PyMySQL 的目标是成为 MySQLdb 的替代品官方文档:pymysql.readthedocs.io/ pymysql 安装 使用 pip 安装使用 Pycharm 界面安装 pip install pymysqlp…...

第二节 linux操作系统安装与配置
一:Vmware虚拟机安装与使用 ①VMware是一个虚拟PC的软件,可以在现有的操作系统上虚拟出一个新的硬件环境,相当于模拟出一台新的PC ,以此来实现在一台机器上真正同时运行多个独立的操作系统。 ②VMware主要特点:…...
ChatGPT 对SEO的影响
ChatGPT 的兴起是否预示着 SEO 的终结? 一点也不。事实上,如果使用得当,它可以让你的 SEO 工作变得更加容易。 强调“正确使用时”。 你可以使用ChatGPT来帮助进行关键字研究的头脑风暴部分、重新措辞你的内容、生成架构标记等等。 但你不…...
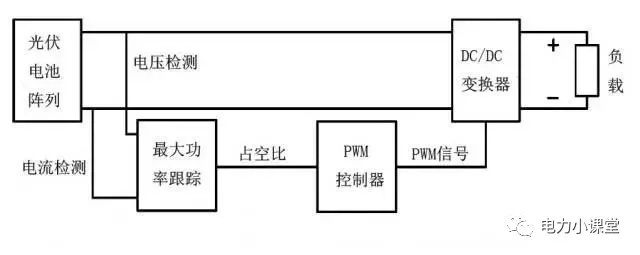
光伏逆变器MPPT的作用、原理及算法
MPPT是逆变器非常核心的技术,MPPT电压在进行光伏电站设计时一项非常关键的参数。 一、什么是MPPT? (单块光伏组件的I-V、P-V曲线) 上图中,光伏组件的输出电压和电流遵循I-V曲线(绿色)、P-V曲线(蓝色),如果…...

一文详解pyspark常用算子与API
rdd.glom() 对rdd的数据进行嵌套,嵌套按照分区来进行 rdd sc.parallelize([1, 2, 3, 4, 5, 6, 7, 8, 9], 2)print(rdd.glom().collect()) 输出:[[1,2,3,4],[5,6,7,8,9]] 参考 PySpark基础入门(2):RDD及其常用算子…...

使用Rollup 搭建开发环境
1 什么是Rollup Rollup 是一个用于 JavaScript 的模块打包工具,它将小的代码片段编译成更大、更复杂的代码,例如库或应用程序。它使用 JavaScript 的 ES6 版本中包含的新标准化代码模块格式,而不是以前的 CommonJS 和 AMD 等特殊解决方案。(开…...
ubuntu:beyond compare 4 This license key has been revoked 解决办法
https://www.cnblogs.com/zhibei/p/12095431.html 错误如图所示: 解决办法: (1)先用find命令找到bcompare所在位置:sudo find /home/ -name *bcompare (2)进入 /home/whf/.config,删除/bco…...

华为交换机生成树STP配置案例
企业内部网络怎么防止网络出现环路?学会STP生成树技术就可以解决啦。 STP简介 在二层交换网络中,一旦存在环路就会造成报文在环路内不断循环和增生,产生广播风暴,从而占用所有的有效带宽,使网络变得无法正常通信。 在…...

Avalonia框架下实现热更新
在Avalonia框架下实现热更新(也称为动态加载或模块化更新),通常涉及程序集的动态加载与卸载,以及UI元素、视图模型或其他应用程序逻辑部分的实时替换。由于Avalonia本身是一个跨平台的GUI框架,并没有直接内置热更新机制…...

适用于各种危险区域的火焰识别摄像机,实时监测、火灾预防、安全监控,为安全保驾护航
火灾是一种极具破坏力的灾难,对人们的生命和财产造成了严重的威胁。为了更好地预防和防范火灾,火焰识别摄像机作为一种先进的监控设备,正逐渐受到人们的重视和应用。本文将介绍火焰识别摄像机在安全监控和火灾预防方面的全面应用方案。 一、火…...
react-router-dom5升级到6
前言 升级前版本为5.1.2 下载与运行 下载 npm install react-router-dom6运行 运行发现报错: 将node_modules删除,重新执行npm i即可 运行发现如下报错 这是因为之前有引用react-router-dom.min,v6中取消了该文件,所以未找到文件导致报错。…...

Linux调试工具—gdb
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:HEART BEAT—YOASOBI 2:20━━━━━━️💟──────── 5:35 🔄 ◀️ ⏸ ▶️ ☰ …...

SpringCloud(H版alibaba)框架开发教程之nacos做配置中心——附源码(2)
上篇主要讲了使用eureka,zk,nacos当注册中心 这篇内容是nacos配置中心 代码改动部分mysql驱动更新到8.0,数据库版本升级到了8.0,nacos版本更新到了2.x nacos2.x链接 链接:https://pan.baidu.com/s/11nObzgTjWisAfOp…...
网络摄像头爆破实战
*** 重要说明:仅用于交流网络安全测试技术,并唤起大家对网络安全的重视,如用本文的技术干违法的事情,博主概不负责。*** 文章目录 前言1. 发现摄像头2. 发现端口3. 确定品牌信息4. 确定RTSP地址5. 获取视频流6. 获取密码7. 再次获…...
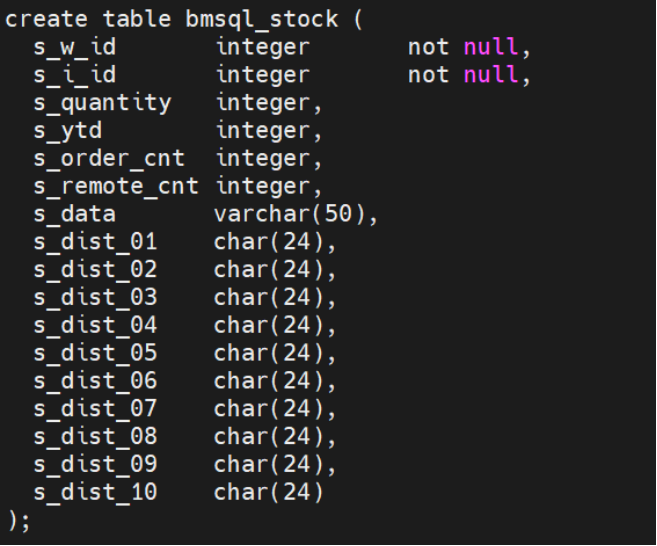
亚信安慧AntDB数据并行加载工具的实现(二)
3.功能性说明 本节对并行加载工具的部分支持的功能进行简要说明。 1) 支持表类型 并行加载工具支持普通表、分区表。 2) 支持指定导入字段 文件中并不是必须包含表中所有的字段,用户可以指定导入某些字段,但是指定的字段数要和文件中的字段数保持一…...

【Java进阶篇】JDK新版本中的新特性都有哪些
JDK新版本中的新特性都有哪些 ✔️经典解析✔️拓展知识仓✔️本地变量类型推断✔️Switch 表达式✔️Text Blocks✔️Records✔️封装类✔️instanceof 模式匹配✔️switch 模式匹配 ✅✔️虚拟线程 ✔️经典解析 JDK 8中推出了Lambda表达式、Stream、Optional、新的日期API等…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
