数据结构--二叉搜索树的实现
目录
1.二叉搜索树的概念
2.二叉搜索树的操作
二叉搜索树的插入
中序遍历(常用于排序)
二叉搜索树的查找
二叉搜索树的删除
完整二叉树代码:
二叉搜索树的应用
key/value搜索模型整体代码
1.二叉搜索树的概念
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值若它的右子树不为空,则右子树上所有节点的值都大于根节点的值它的左右子树也分别 为二叉搜索树

#include<iostream>
using namespace std;template<class K>//搜索二叉树的结点
struct BSTreeNode
{K _key;BSTreeNode<K>* _left;BSTreeNode<K>* _right;BSTreeNode(const K& s = K()):_key(s), _left(nullptr), _right(nullptr){}
};template<class K>//搜索二叉树
class BSTree
{
public:BSTree():_root(nullptr){}//...各种操作二叉搜索树方法的实现//...
private:typedef BSTreeNode<K> Node;Node* _root;
};2.二叉搜索树的操作
二叉搜索树的插入
这里根据二叉搜索树的概念分两种情况:
a. 树为空,则直接新增节点,赋值给 root 指针b. 树不空,按二叉搜索树性质查找插入位置,插入新节点
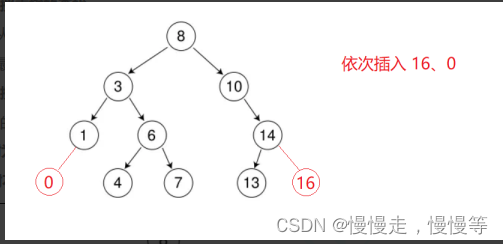
非递归
bool Insert(const K & key){if (_root == nullptr)//情况a{_root = new Node(key);}else//情况b{Node* parent = nullptr;//记录当前节点的父结点Node* cur = _root;while (cur){if (cur->_key > key)//小于当前节点的值,向左走{parent = cur;cur = cur->_left;}else if (cur->_key < key)//大于当前结点的值,向右走{parent = cur;cur = cur->_right;}else //数字重复插入失败{return false;}}cur = new Node(key);if (parent->_key > key)//判断插入结点是在parent的左子树还是右子树{parent->_left = cur;}else{parent->_right = cur;}return true;}}为什么要定义parent变量记录cur的父节点?
这里我们要知道,cur=new Node(key)这行代码的真正意义是给cur赋值,并没有把结点插入到树中。
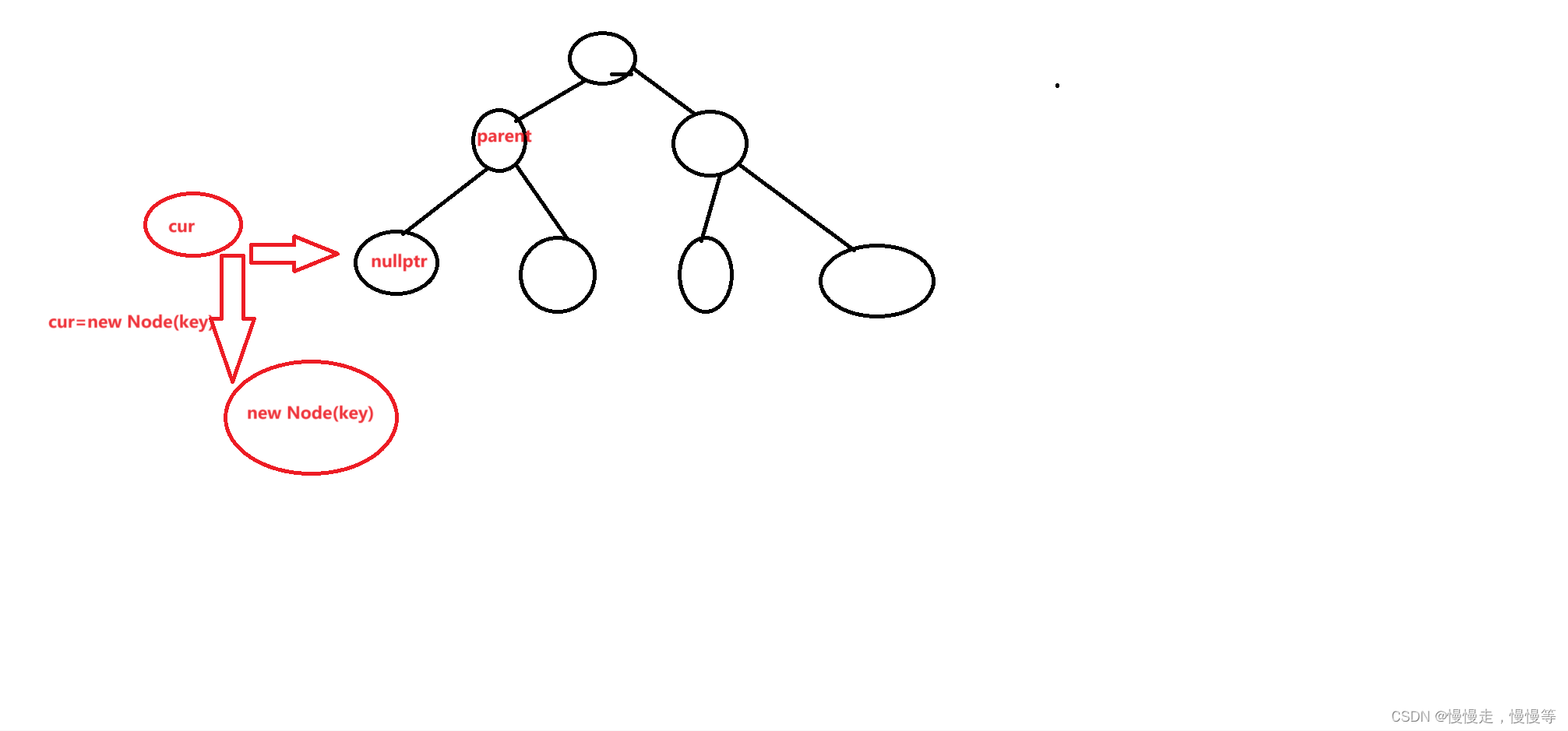
注:在向二叉搜索树插入时,一定要判断是在父节点的左子树还是右子树。
递归:
public:
bool InsertR(const K& key)
{return _insertR(_root, key);
}private:
bool _insertR(Node*& root, const K& key)
{if (root == nullptr){root = new Node(key);return true;}else{if (root->_key > key){return _insertR(root->_left, key);}else if (root->_key < key){return _insertR(root->_right, key);}else{return false;}}
}注:由于使用递归时,需要用到成员变量_root作为实参,但是在类外面无法直接调用,因此,将递归调用的函数封装到了InsertR()里面。
为什么这里不用记录父节点,就可以插入到树中。
这里我们要注意函数的第一个变量,我们使用了引用!
这里的root就是父节点的左孩子或有孩子。
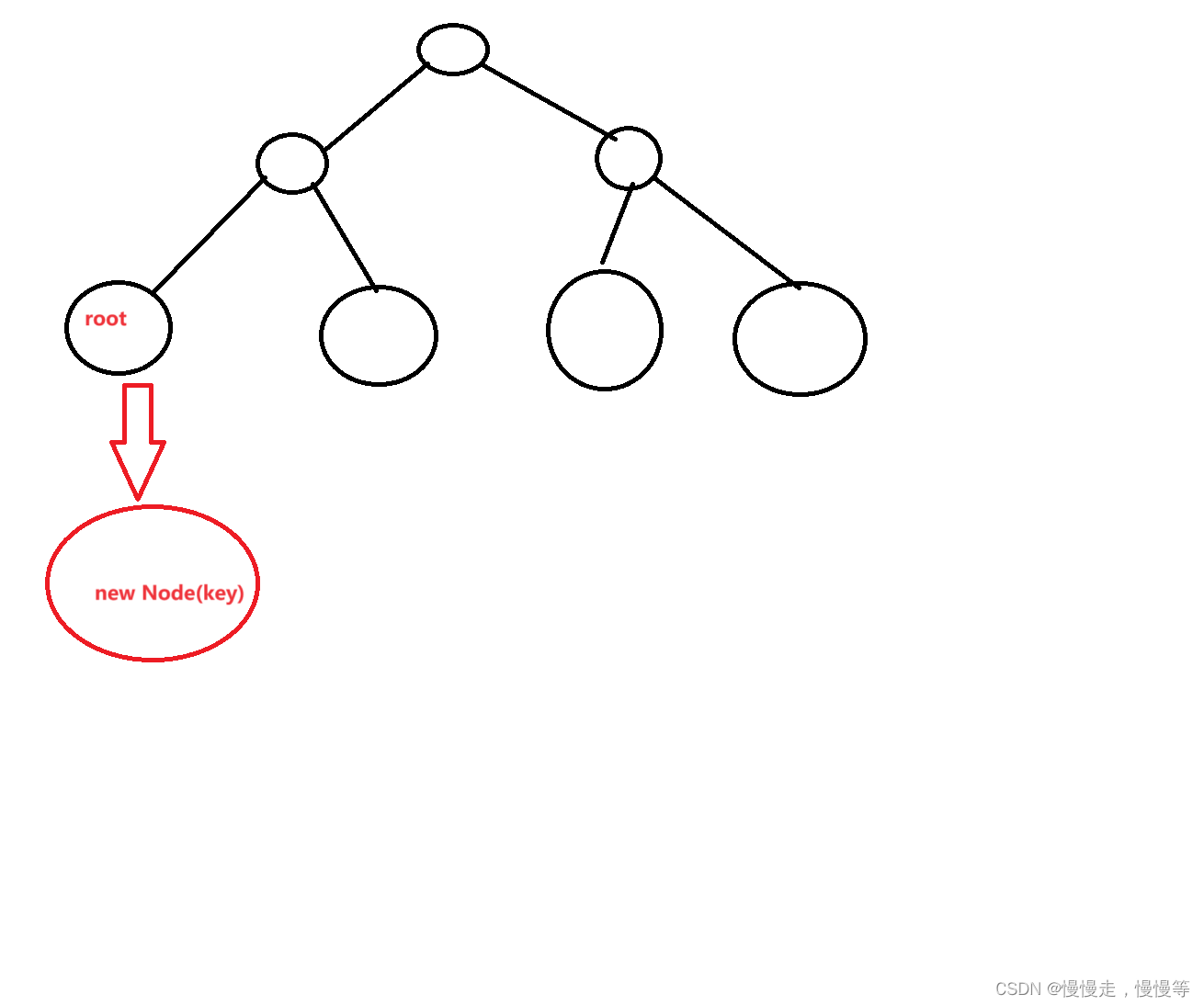
中序遍历(常用于排序)
public:
void Inorder()
{_Inorder(_root);
}private:
void _Inorder(Node* root)
{if (root == nullptr)return;_Inorder(root->_left);cout << root->_key << " ";_Inorder(root->_right);
}这里根据二叉搜索树的概念我们清楚,其中序遍历相当于将树里面的数据按从小到大排序输出。
二叉搜索树的查找
查找方法:
a 、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。b 、最多查找高度次,走到到空,还没找到,这个值不存在。
注意:
为完全二叉树时间复杂度最好,为O(log n)
树的结点全部为左孩子或右孩子时,时间复杂度最坏,为O(n)
非递归
bool Find(const K& key)
{if (_root == nullptr)//树为空return false;Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->left;// _key>key.左走}else if (cur->_key < key){cur = cur->_right;//_key<key.右走}else{return true;//相等,找到}}return false;//没有一个相等
}递归:
public:
Node* FindR(const K& key)
{return _FindR(_root, key);
}private:
Node* _FindR(Node* root, const K& key)
{if (root == nullptr)return nullptr;if (root->_key > key){_FindR(root->_left, key);}else if (root->_key < key){_FindR(root->_right, key);}else{return root;}
}二叉搜索树的删除
a. 要删除的结点无孩子结点b. 要删除的结点只有左孩子结点c. 要删除的结点只有右孩子结点d. 要删除的结点有左、右孩子结点
情况 b :删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点 -- 直接删除情况 c :删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点 -- 直接删除情况 d :在它的右子树中寻找中序下的第一个结点 ( 关键码最小 ) ,用它的值填补到被删除节点中,再来处理该结点的删除问题 -- 替换法删除
bool Erase(const K& key)
{if (_root == nullptr)return false;Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = nullptr;cur = cur->_right;}else{if (cur->_left == nullptr)//情况a{if (cur == _root)//特殊条件,等于根节点{_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->right == nullptr)//情况b{if (cur == _root) //特殊条件,等于根节点{_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else //情况c{Node* parent = cur;Node* subnode = cur->_right;while (subnode->_left){parent = subnode;subnode = subnode->_left;}swap(cur->_key, subnode->_key);if (parent->_right == subnode) //当cur->_right->left==nullptr{parent->_right = subnode->_right;}else{parent->_left = subnode->_right;}delete subnode;}return true;}}return false;
}递归:
public:bool EraseR(const K& key)
{_EraseR(_root,key);
}private:bool _EraseR(Node*& root, const K& key)
{if (root == nullptr){return false;}if (root->_key > key){return _EraseR(root->_left, key);}else if (root->_key < key){return _EraseR(root->_right, key);}else{if (root->_left == nullptr){Node* temp = root;root = root->_right;delete temp;}else if (root->right){Node* temp = root;root = root->_left;delete temp;}else{Node* subnode = root->_right;while (subnode->left){subnode = subnode->_left;}swap(root->_key, subnode->_key);return _EraseR(root - right, key);}}
}完整二叉树代码:
#include<iostream>
using namespace std;template<class K>//搜索二叉树的结点
struct BSTreeNode
{K _key;BSTreeNode<K>* _left;BSTreeNode<K>* _right;BSTreeNode(const K& s = K()):_key(s), _left(nullptr), _right(nullptr){}
};template<class K>//搜索二叉树
class BSTree
{
public:BSTree():_root(nullptr){}bool Insert(const K & key){if (_root == nullptr)//情况a{_root = new Node(key);}else//情况b{Node* parent = nullptr;//记录当前节点的父结点Node* cur = _root;while (cur){if (cur->_key > key)//小于当前节点的值,向左走{parent = cur;cur = cur->_left;}else if (cur->_key < key)//大于当前结点的值,向右走{parent = cur;cur = cur->_right;}else //数字重复插入失败{return false;}}cur = new Node(key);if (parent->_key > key)//判断插入结点是在parent的左子树还是右子树{parent->_left = cur;}else{parent->_right = cur;}return true;}}bool Find(const K& key){if (_root == nullptr)//树为空return false;Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->left;// _key>key.左走}else if (cur->_key < key){cur = cur->_right;//_key<key.右走}else{return true;//相等,找到}}return false;//没有一个相等}Node* FindR(const K& key){return _FindR(_root, key);}void Inorder(){_Inorder(_root);}bool InsertR(const K& key){return _insertR(_root, key);cout << endl;}bool Erase(const K& key){if (_root == nullptr)return false;Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if(cur->_key<key){parent = nullptr;cur = cur->_right;}else{if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if(cur->right==nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{Node* parent = cur;Node* subnode = cur->_right;while (subnode->_left){parent = subnode;subnode = subnode->_left;}swap(cur->_key, subnode->_key);if (parent->_right == subnode){parent->_right = subnode->_right;}else{parent->_left = subnode->_right;}delete subnode;}return true;}}return false;}bool EraseR(const K& key){return _EraseR(_root, key);}private:typedef BSTreeNode<K> Node;Node* _root;bool _insertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}else{if (root->_key > key){return _insertR(root->_left, key);}else if (root->_key < key){return _insertR(root->_right, key);}else{return false;}}}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_key<<" ";_Inorder(root->_right);}Node*_FindR(Node* root, const K& key){if (root == nullptr)return nullptr;if (root->_key > key){_FindR(root->_left, key);}else if (root->_key < key){_FindR(root->_right, key);}else{return root;}}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key > key){return _EraseR(root->_left, key);}else if (root->_key < key){return _EraseR(root->_right, key);}else{if (root->_left == nullptr){Node* temp = root;root = root->_right;delete temp;}else if (root->right){Node* temp = root;root = root->_left;delete temp;}else{Node* subnode = root->_right;while (subnode->left){subnode = subnode->_left;}swap(root->_key, subnode->_key);return _EraseR(root - right, key);}}}
};二叉搜索树的应用
key/value搜索模型整体代码
#pragma once
// 改造二叉搜索树为KV结构
template<class K, class V>
struct BSTNode
{BSTNode(const K& key = K(), const V& value = V()): _pLeft(nullptr), _pRight(nullptr), _key(key), _Value(value){}BSTNode<T>* _pLeft;BSTNode<T>* _pRight;K _key;V _value
};template<class K, class V>
class BSTree
{typedef BSTNode<K, V> Node;
public:bool Insert(const K& key,const V& value){if (_root == nullptr)//情况a{_root = new Node(key,value);}else//情况b{Node* parent = nullptr;//记录当前节点的父结点Node* cur = _root;while (cur){if (cur->_key > key)//小于当前节点的值,向左走{parent = cur;cur = cur->_left;}else if (cur->_key < key)//大于当前结点的值,向右走{parent = cur;cur = cur->_right;}else //数字重复插入失败{return false;}}cur = new Node(key,value);if (parent->_key > key)//判断插入结点是在parent的左子树还是右子树{parent->_left = cur;}else{parent->_right = cur;}return true;}}bool Find(const K& key){if (_root == nullptr)//树为空return false;Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->left;// _key>key.左走}else if (cur->_key < key){cur = cur->_right;//_key<key.右走}else{return true;//相等,找到}}return false;//没有一个相等}bool Erase(const K& key){if (_root == nullptr)return false;Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = nullptr;cur = cur->_right;}else{if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{Node* parent = cur;Node* subnode = cur->_right;while (subnode->_left){parent = subnode;subnode = subnode->_left;}swap(cur->_key, subnode->_key);if (parent->_right == subnode){parent->_right = subnode->_right;}else{parent->_left = subnode->_right;}delete subnode;}return true;}}return false;}void Inorder(){_Inorder(_root);}private:Node* _root;void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_key << ":"<<root->_value<<endl;_Inorder(root->_right);}
};相关文章:
数据结构--二叉搜索树的实现
目录 1.二叉搜索树的概念 2.二叉搜索树的操作 二叉搜索树的插入 中序遍历(常用于排序) 二叉搜索树的查找 二叉搜索树的删除 完整二叉树代码: 二叉搜索树的应用 key/value搜索模型整体代码 1.二叉搜索树的概念 二叉搜索树又称二叉排序树,它或者是一…...

《微信小程序开发从入门到实战》学习六十八
6.6 网络API 6.6.1 网络API 使用wx.request接口可以发起网络请求。该接口接受一个Object参,参数支持属性如下所示: url(必填):开发者服务器地址 data:请求的参数,类型为string/object/ArrayBuffer header…...

阿里是如何去“O”的?
大家好,我是老猫,猫头鹰的“猫”。 今天我们来聊聊数据库这个话题。 2009年,阿里提出“去IOE化”的概念,这在当时看起来是天方夜谭,但目前来看可以说是"轻舟已过万重山"。 IOE是传统IT三大件,…...

蓝桥杯备赛 day 1 —— 递归 、递归、枚举算法(C/C++,零基础,配图)
目录 🌈前言 📁 枚举的概念 📁递归的概念 例题: 1. 递归实现指数型枚举 2. 递归实现排列型枚举 3. 递归实现组合型枚举 📁 递推的概念 例题: 斐波那契数列 📁习题 1. 带分数 2. 反硬币 3. 费解的…...

87 双指针解验证回文字符串II
问题描述:简单给定一个非空字符串s,最多删除一个字符,判断是否成为回文字符串。 双指针解法:指针1指向开头,指针2指向结尾,定义一个count记录不满足回文串的数量,若超过1,则返回fal…...

【排序算法】【二叉树】【滑动窗口】LeetCode220: 存在重复元素 III
作者推荐 【二叉树】【单调双向队列】LeetCode239:滑动窗口最大值 本文涉及的基础知识点 C算法:滑动窗口总结 题目 给你一个整数数组 nums 和两个整数 indexDiff 和 valueDiff 。 找出满足下述条件的下标对 (i, j): i ! j, abs(i - j) < indexDi…...
OS 7--DNS配置+Apache发布网站
环境准备 centOS 7 1.配置DNS 1.1 域名为lianxi.com 1.2 为WWW服务器、FTP服务器、NEWS服务器做域名解析 1)安装DNS yum -y install bind bind-utils (如果安装不上,就把磁盘在重洗挂载一下) 2)修改DNS配置文件 vim /etc/resolv.conf…...

1月2日代码随想录二叉树的最小深度及层序遍历总结
个人认为这么一个层序遍历的章节放这么多基本一样的题目算是很没意思的了 填充每个节点的下一个右侧节点和二叉树最大深度和前面的代码几乎完全一样,所以我就跳过了 代码随想录 (programmercarl.com) 代码随想录 (programmercarl.com) 111.二叉树的最小深度 给…...
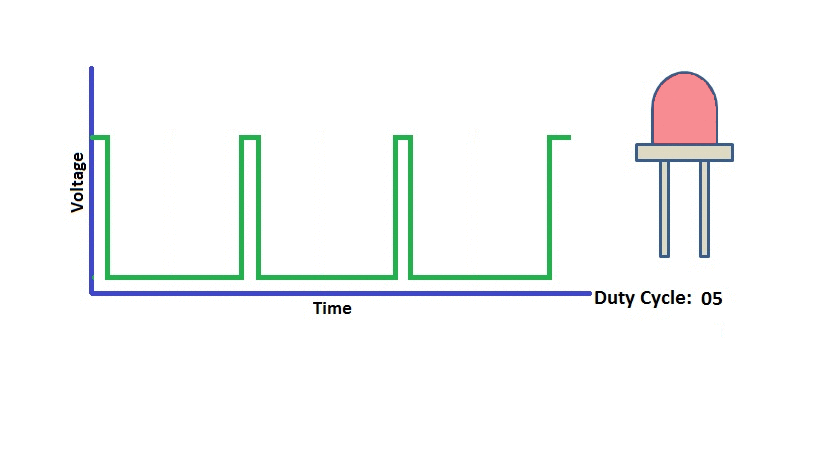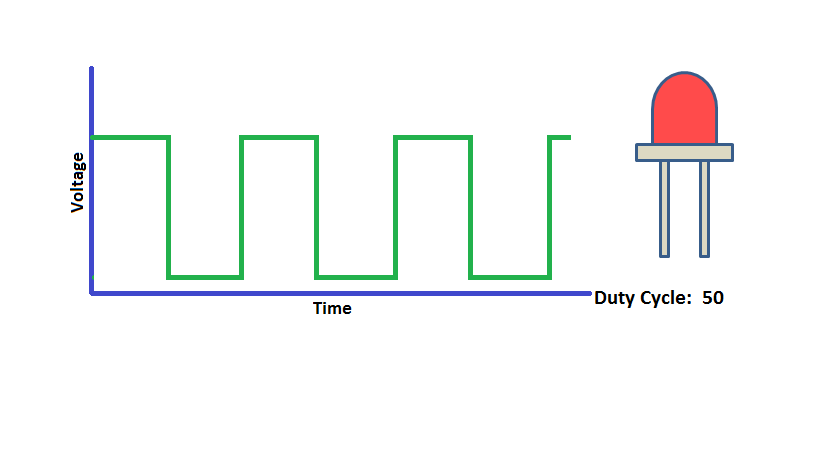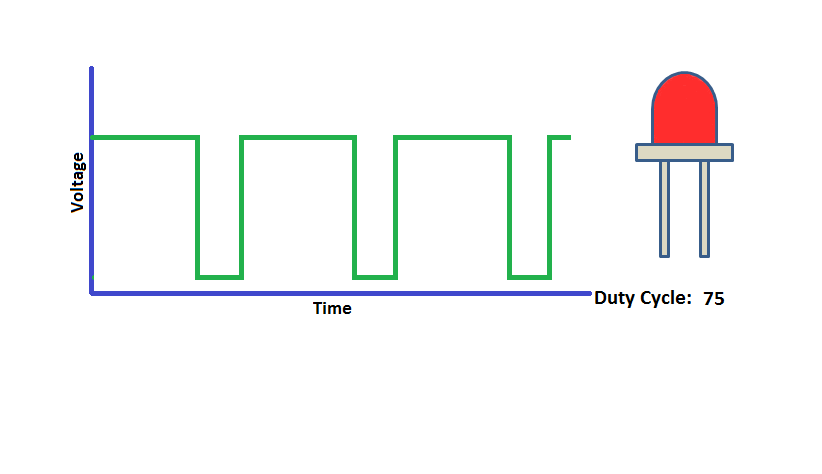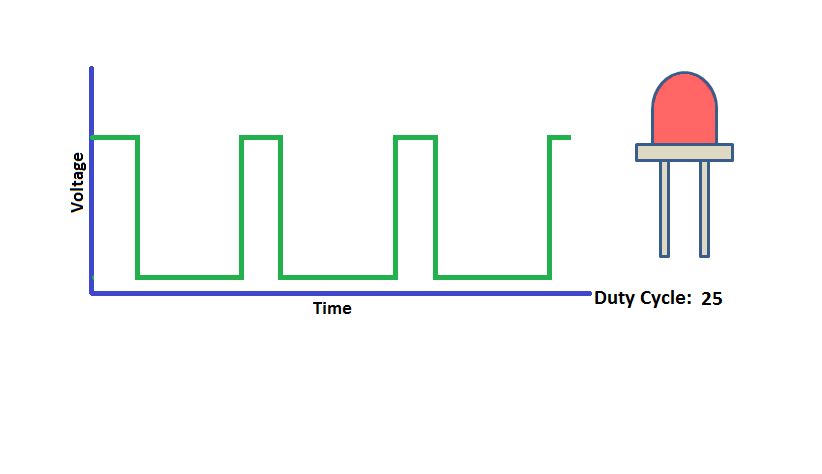
RK3568平台开发系列讲解(Linux系统篇)PWM系统编程
🚀返回专栏总目录 文章目录 一、什么是PWM二、PWM相关节点三、PWM应用编程沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇将介绍 PWM 的系统编程。 一、什么是PWM PWM,即脉冲宽度调制(Pulse Width Modulation)...

Linux CPU 数据 Metrics 指标解读
过去从未仔细了解过使用 top 和 htop 等命令时显式的CPU信息,本文我们详解解读和标注一下各个数据项的含义,同时和 Ganglia 显式的数据做一个映射。开始前介绍一个小知识,很多查看CPU的命令行工具都是 cat /proc/stat 里的数据,所…...
Ansible自动化运维(一)简介及部署、清单
👨🎓博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 🐋 希望大家多多支…...

深度学习MLP_实战演练使用感知机用于感情识别_keras
目录 (1)why deep learning is game changing?(2)it all started with a neuron(3)Perceptron(4)Perceptron for Binary Classification(5)put it all toget…...
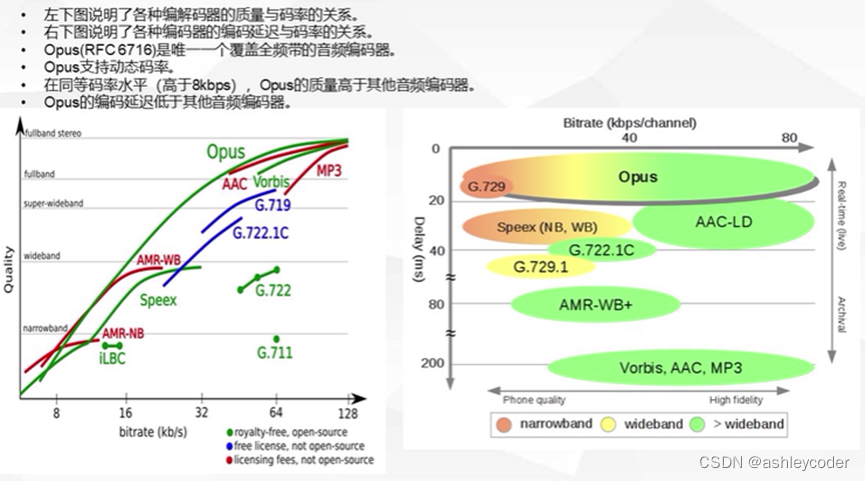
[ffmpeg系列 02] 音视频基本知识
一 视频 RGB: AV_PIX_FMT_RGB24, ///< packed RGB 8:8:8, 24bpp, RGBRGB… Y:明亮度, Luminance或luma, 灰阶图, UV:色度,Chrominance或Chroma。 YCbCr: Cb蓝色分量,Cr是红色分量。 取值范围ÿ…...

【ASP.NET Core 基础知识】--目录
介绍 1.1 什么是ASP.NET Core1.2 ASP.NET Core的优势1.3 ASP.NET Core的版本历史 环境设置 2.1 安装和配置.NET Core SDK2.2 使用IDE(Integrated Development Environment):Visual Studio Code / Visual Studio 项目结构 3.1 ASP.NET Core项…...

java数据结构与算法刷题-----LeetCode509. 斐波那契数
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 很多人觉得动态规划很难,但它就是固定套路而已。其实动态规划只…...
)
vue3 element plus el-table封装(二)
上文是对el-table的基本封装,只能满足最简单的应用,本文主要是在上文的基础上增加slot插槽,并且对col插槽进行拓展,增加通用性 // BaseTable.vue <template><el-table><template v-for"name in tableSlots&…...

cnn lstm结合网络
目录 特征处理例子: cnn 5张图片一组,提取特征后,再给lstm,进时间序列分类。 特征处理例子: import torch# 假设 tensor 是形状为 15x64 的张量 tensor torch.arange(15 * 2).reshape(15, 2) # 生成顺序编号的张量&…...

Ubuntu连接xshell
安装ssh服务器 sudo apt-get install openssh-server 重启ssh sudo service ssh restart 3.启动ssh服务 /etc/init.d/ssh start4.修改文件,允许远程登陆 sudo vi /etc/ssh/sshd_config PermitRootLogin prohibit-password #默认为禁止登录 PermitRootLogin y…...
nginx安装和配置
目录 1.安装 2.配置 3.最小配置说明 4. nginx 默认访问路径 1.安装 使用 epel 源安装 先安装 yum 的扩展包 yum install epel-release -y 再安装 nginx yum install nginx -y 在启动nginx 前先关闭防火墙 systemctl stop firewalld 取消防火墙开机自启 systemctl di…...

【头歌实训】kafka-入门篇
文章目录 第1关:kafka - 初体验任务描述相关知识Kafka 简述Kafka 应用场景Kafka 架构组件kafka 常用命令 编程要求测试说明答案代码 第2关:生产者 (Producer ) - 简单模式任务描述相关知识Producer 简单模式Producer 的开发步骤Ka…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
