【数据结构】二叉搜索(查找/排序)树
一、二叉搜索树基本概念
1、定义
二叉搜索树,又称为二叉排序树,二叉查找树,它满足如下四点性质:
1)空树是二叉搜索树;
2)若它的左子树不为空,则左子树上所有结点的值均小于它根结点的值;
3)若它的右子树不为空,则右子树上所有结点的值均大于它根结点的值;
4)它的左右子树均为二叉搜索树;
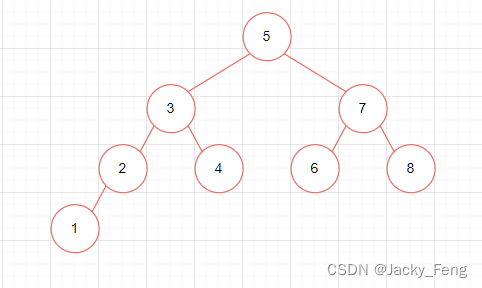
如上图所示:二叉搜索树的任何一棵子树,它的根结点的值一定大于左子树所有结点的值,且一定小于右子树所有结点的值。如果对二叉搜索树进行中序遍历,我们可以发现,得到的序列是一个递增序列,上述的遍历结果为[1,2,3,4,5,6,7,8]。
如果要查找4,只需要从根结点比较查找3次就能找到,可以显著提高搜索的速度。
二、二叉搜索树基础操作
1、查找算法
(1)查找原理
在二叉搜索树中查找某个数是否存在,存在返回 true,不存在返回 false。
对于要查找的数 val ,从根结点出发,总共四种情况依次判断:
1)若二叉搜索树为空树,直接返回 false;
2) val 的值 等于 树根结点的值,则直接返回 true;
3) val 的值 小于 树根结点的值,说明 val 对应的结点不在根结点,也不在右子树上,需要在左子树上查找,递归返回左子树的查找结果;
4) val 的值 大于 树根结点的值,说明 val 对应的结点不在根结点,也不在左子树上,需要在右子树上查找,递归返回右子树的查找结果;
(2)查找算法源码
① 结点源码
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}};② 查找算法源码 (深度优先,递归查找)
bool BSTFind(TreeNode* root, int val)
{if (root == nullptr) {return false;}if (root->val == val) {return true;}if (val < root->val) {return BSTFind(root->left, val);}else {return BSTFind(root->right, val);}
}2、插入算法
(1)插入原理
将给定的值 val 生成结点后,插入到树上的某个位置,并且保持这棵树还是二叉搜索树。对于要插入的值 val ,从根结点出发,总共四种情况依次判断:
1)若为空树,则创建一个值为 val 的结点并且返回根结点;
2) val 的值 等于 树根结点的值,无须执行插入,直接返回根结点;
3) val 的值 小于 树根结点的值,那么插入位置一定在 左子树,递归执行插入左子树的过程,并且返回插入结果作为新的左子树;
4) val 的值 大于 树根结点的值,那么插入位置一定在 右子树,递归执行插入右子树的过程,并且返回插入结果作为新的右子树;
(2) 插入源码
TreeNode* BSTInsert(TreeNode* root, int val) {if (root == nullptr) {root = new TreeNode(val);return root;}if (val == root->val) {return root;}if (val < root->val) {root->left = BSTInsert(root->left, val);}else {root->right = BSTInsert(root->right, val);}return root;
}3、删除算法
(1)删除原理
删除值为 val 结点,从根结点出发,总共四种情况依次判断:
1)空树,不存在结点直接返回空树;
2) val 的值 小于 树根结点的值,则需要删除的结点一定不在右子树上,递归调用删除左子树的对应结点;
3) val 的值 大于 树根结点的值,则需要删除的结点一定不在左子树上,递归调用删除右子树的对应结点;
4) val 的值 等于 树根结点的值,相当于是要删除根结点,这时候又要分三种情况:
- 当前树只有左子树,则直接将左子树返回,并且释放当前树根结点的空间;
- 当前树只有右子树,则直接将右子树返回,并且释放当前树根结点的空间;
- 当左右子树都存在时,需要在右子树上找到一个值最小的结点,替换新的树根,而其它结点组成的树作为它的子树;
(2)删除源码
由上述删除算法原理可知,删除结点之前可能还需要找最小结点,所以需要定义查找最小结点接口。
int BSTFindMin(TreeNode* root) {if (root->left)return BSTFindMin(root->left); return root->val;
}查找根为 root ,值最小的那个结点的值,根据二叉搜索树的性质,如果左子树存在,则必然存在更小的值,递归搜索左子树,且最小值结点为叶子结点;如果左子树不存在,则根结点的值必然最小,直接返回。
删除根结点,并返回新根结点
//删除根结点并返回新根结点
TreeNode* Delete(TreeNode* root) {TreeNode* delNode, * retNode;if (root->left == nullptr) {delNode = root;retNode = root->right;delete delNode;delNode = nullptr;}else if (root->right == nullptr) {delNode = root;retNode = root->left;delete delNode;delNode = nullptr;}else {retNode = BSTFindMin(root->right);retNode->left = root->left;retNode->right = root->right;delete root;root = nullptr;}return retNode;
}- 如果左子树为空,则用右子树做为新的树根;
- 如果右子树为空,则用左子树作为新的树根;
- 否则,当左右子树都为非空时,利用 BSTFindMin ,从右子树上找出最小的结点,作为新的根。
删除指定值的结点
//删除指定结点
TreeNode* BSTDelete(TreeNode* root, int val) {if (nullptr == root) {return nullptr; }if (val == root->val) {return Delete(root); }else if (val < root->val) {root->left = BSTDelete(root->left, val); }else if (val > root->val) {root->right = BSTDelete(root->right, val); }return root;
}- 如果为空树,则直接返回空结点;
- 如果需要删除的结点的值 等于 树根结点的值,则直接调用接口 Delete ;
- 如果需要删除的结点的值 小于 树根结点的值,则需要删除的结点必定在左子树上,递归调用左子树的删除,并且将返回值作为新的左子树的根结点;
- 如果需要删除的结点的值 大于 树根结点的值,则需要删除的结点必定在右子树上,递归调用右子树的删除,并且将返回值作为新的右子树的根结点;
- 返回当前树的根结点;
相关文章:

【数据结构】二叉搜索(查找/排序)树
一、二叉搜索树基本概念 1、定义 二叉搜索树,又称为二叉排序树,二叉查找树,它满足如下四点性质: 1)空树是二叉搜索树; 2)若它的左子树不为空,则左子树上所有结点的值均小于它根结…...
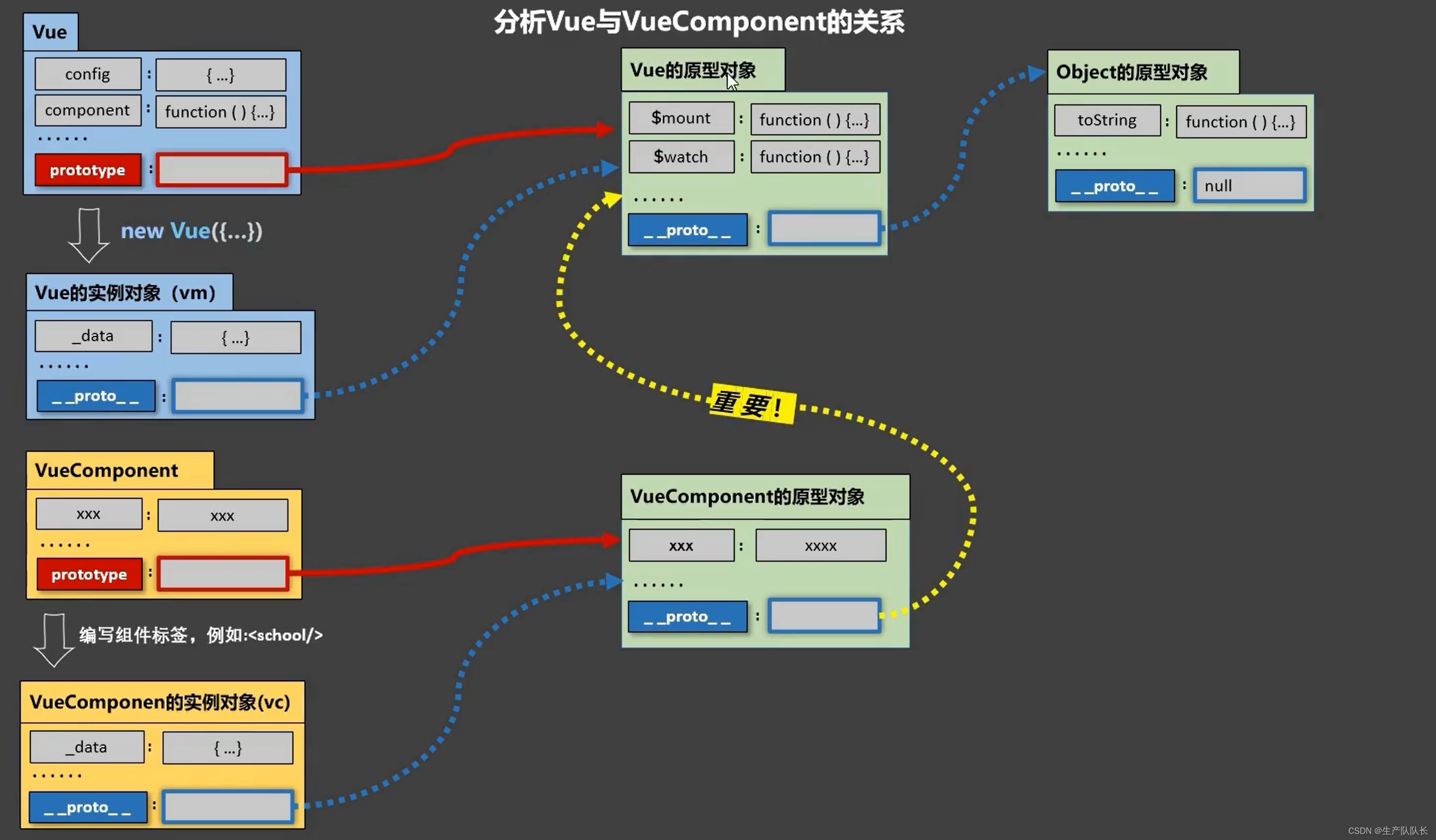
Vue:Vue与VueComponent的关系图
1.一个重要的内置关系:VueComponent.prototype.proto Vue.prototype 2.为什么要有这个关系:让组件实例对象(vc)可以访问到 Vue原型上的属性、方法。 案例证明: <!DOCTYPE html> <html lang"en"&…...

Elasticsearch8集群部署
转载说明:如果您喜欢这篇文章并打算转载它,请私信作者取得授权。感谢您喜爱本文,请文明转载,谢谢。 本文记录在3台服务器上离线搭建es8.7.1版本集群。 1. 修改系统配置 1.1 hosts配置 在三台es节点服务器加入hostname解析&…...

【小白专用】c# 如何获取项目的根目录
1、取得控制台应用程序的根目录方法 方法1、Environment.CurrentDirectory 取得或设置当前工作目录的完整限定路径 方法2、AppDomain.CurrentDomain.BaseDirectory 获取基目录,它由程序集冲突解决程序用来探测程序集 2、取得Web应用程序的根目录方法 方法1、HttpRun…...

【PXIE301-208】基于PXIE总线架构的Serial RapidIO总线通讯协议仿真卡
板卡概述 PXIE301-208是一款基于3U PXIE总线架构的Serial RapidIO总线通讯协议仿真卡。该板卡采用Xilinx的高性能Kintex系列FPGA作为主处理器,实现各个接口之间的数据互联、处理以及实时信号处理。板卡支持4路SFP光纤接口,支持一个PCIe x8主机接口&…...

软件测试/测试开发丨Windows系统chromedriver安装与环境变量配置
一、selenium 环境配置 1、chrome 浏览器的安装与配置 目前比较常用的浏览器是 Google Chrome 浏览器,所以本教程以 chrome 为主,后面简介一下其他浏览器的环境配置。 (1)chrome 下载: www.google.cn/chrome/ (2&a…...

【vim 学习系列文章 3.1 -- vim 删除 ^M】
请阅读【嵌入式开发学习必备专栏 之 VIM 专栏】 文章目录 ^M 来源^M 删除 ^M 来源 在 Vim 中打开文件时,您可能会遇到行尾的 ^M 字符,这通常是因为文件使用了 Windows 风格的回车换行符(CRLF),而不是 Unix/Linux 风格…...

深入理解 C# 中的字符串比较:String.CompareTo vs String.Equals
深入理解 C# 中的字符串比较:String.CompareTo vs String.Equals 在处理字符串时,了解如何正确比较它们对于编写清晰、有效和可靠的 C# 程序至关重要。本文将深入探讨 C# 中的两个常用字符串比较方法:String.CompareTo 和 String.Equals&…...
DevOps持续交付之容器化CICD流水线
DevOps持续交付 随着DevOps⼤规模化的落地和应⽤,持续集成以及持续交付已经是⼀种常态的。CI指的是持续集成,使⽤的开源⼯具是Jenkins,CD指的是持续交付和持续部署,⼀个完整的软件开发⽣命周期为: 主要流程可以具体为: 构建阶段…...

Linux/Unix/国产化操作系统常用命令(二)
目录 后CentOS时代国产化操作系统国产化操作系统有哪些常用Linux命令关于Linux的LOGO 后CentOS时代 在CentOS 8发布后,就有了一些变化和趋势,可以说是进入了"后CentOS时代"。这个时代主要表现在以下几个方面: CentOS Stream的引入…...

基于SpringBoot的智慧生活商城系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的智慧生活商城系统,java…...
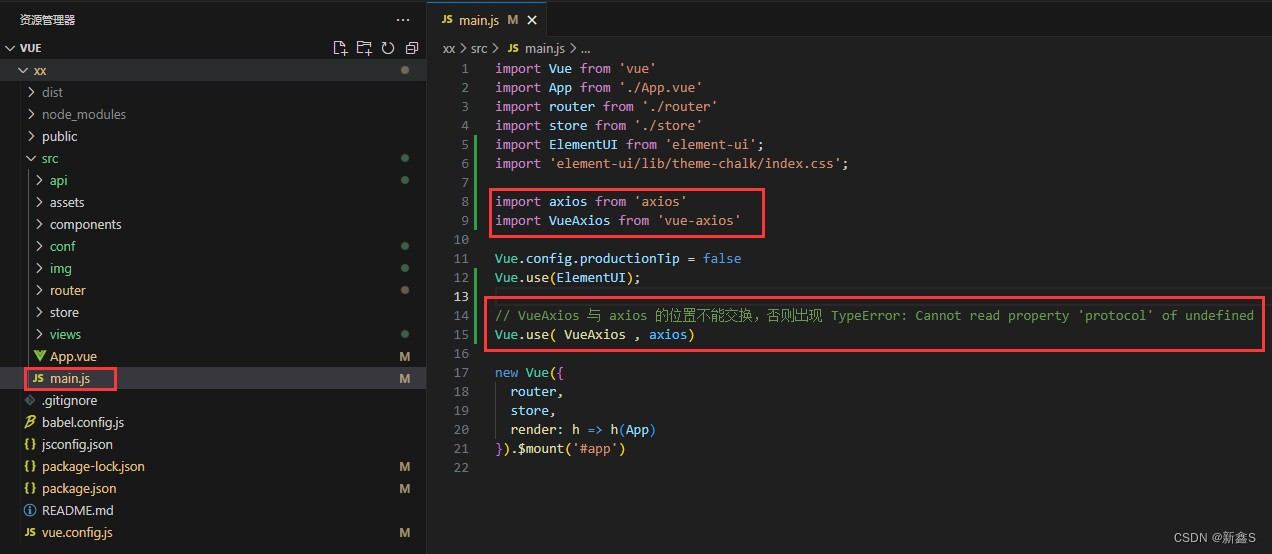
Vue框架引入Axios
首先已经创建好了 Vue 框架,安装好了 node.js。 没有完成的可按照此博客搭建:搭建Vue项目 之后打开终端,使用命令。 1、命令安装 axios 和 vue-axios npm install axios --save npm install vue-axios --save2、package.json 查看版本 在 p…...

EasyExcel 通过模板 导入、导出、下载模板
EasyExcel 通过模板 导入、导出、下载模板 import lombok.AllArgsConstructor; import lombok.Builder; import lombok.Data; import lombok.NoArgsConstructor;import javax.validation.constraints.NotBlank; import javax.validation.constraints.Pattern; import java.io.…...
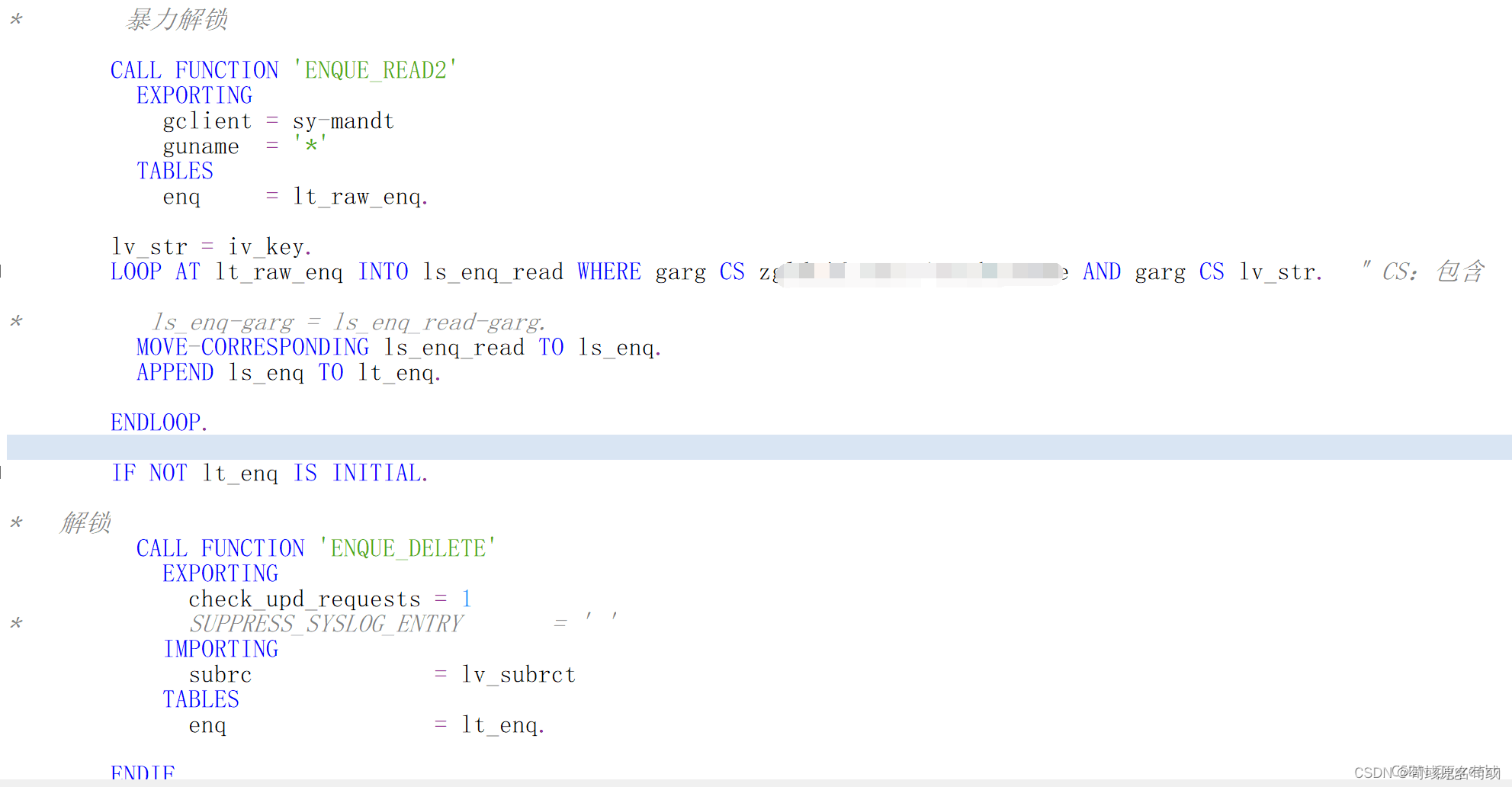
SAP ABAP通过代码解锁SM12中被锁定目标<转载>(RFC: ENQUEUE_READ和 ENQUE_DELETE)
原文链接:https://blog.csdn.net/sinat_38119716/article/details/121406275 备注 RFC:ENQUEUE_READ 读取的是SM12的数据 RFC:ENQUEUE_READ2 读取的是SMENQ的数据 SM12 和 SMENQ 的数据其实是一样的,只是一个是旧的TCODE 一个是新的 解锁用的都是RFC: …...
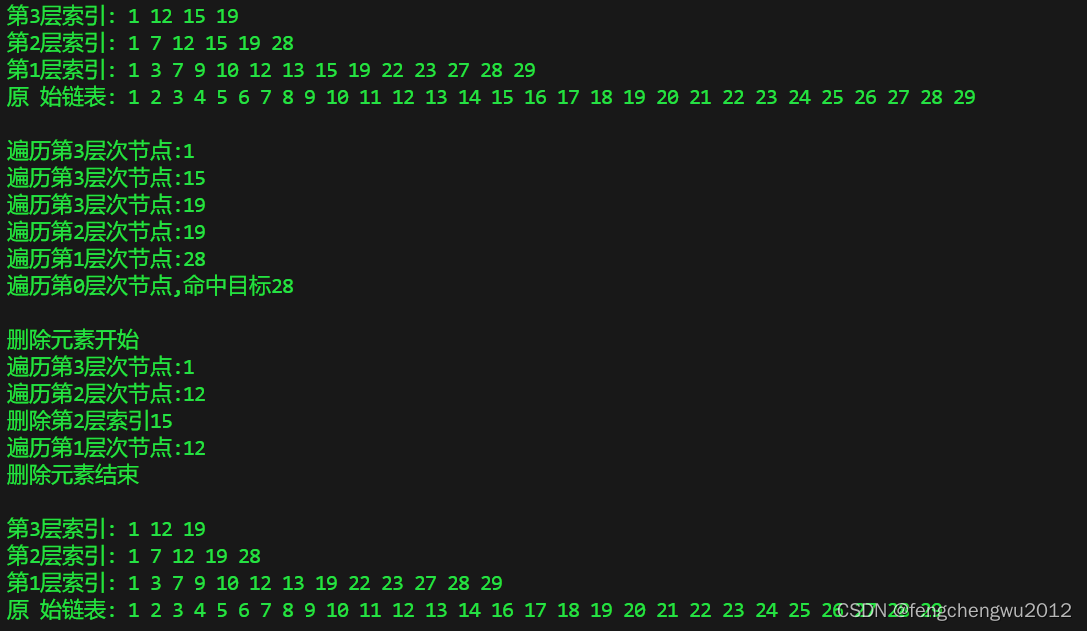
跳跃表原理及实现
一、跳表数据结构 跳表是有序表的一种,其底层是通过链表实现的。链表的特点是插入删除效率高,但是查找节点效率很低,最坏的时间复杂度是O(N),那么跳表就是解决这一痛点而生的。 为了提高查询效率,我们可以给链表加上索…...

详解Vue3中的鼠标事件mousemove、mouseover和mouseout
本文主要介绍Vue3中的常见鼠标事件mousemove、mouseover和mouseout。 目录 一、mousemove——鼠标移动事件二、mouseover——鼠标移入事件三、mouseout——鼠标移出事件 下面是Vue 3中常用的鼠标事件mousemove、mouseover和mouseout的详解。 一、mousemove——鼠标移动事件 鼠…...

Java:socket编程
目录 1、主程序 2、socket任务类 3、jdbc任务类 4、tomcat-jdbc连接池 5、jar包依赖 1、主程序 创建2个线程池,一个用于管理socket连接,一个用来管理jdbc连接。 package socket;import java.io.IOException; import java.net.ServerSocket; import…...
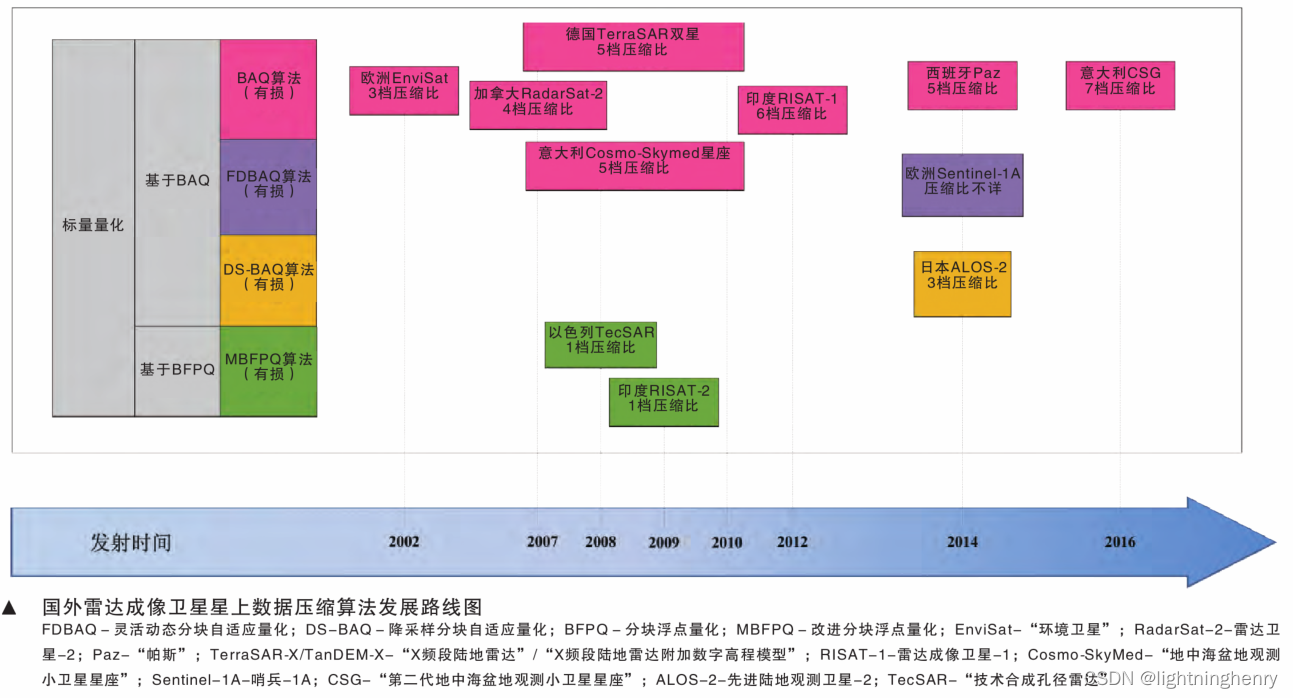
哨兵1号回波数据(L0级)FDBAQ压缩算法详解
本专栏目录: 全球SAR卫星大盘点与回波数据处理专栏目录-CSDN博客 1. 全球SAR卫星回波数据压缩算法统计 各国的SAR卫星的压缩算法按照时间轴排列如下: 可以看出传统的分块BAQ压缩算法(上图粉色)仍然是主流,哨兵1号其实也有传统的BAQ压缩模式。 本文介绍哨兵1号用的FDBAQ算…...

盾构机数据可视化监控平台 | 图扑数字孪生
2002 年,中国 863 计划把盾构机列为国家关键技术,以国家力量为主导,集中力量进行盾构机专项研究。在 2008 年,中国成功研制出属于自己的国产盾构机——中国中铁一号,同时还打通了天津地铁 1500m 的隧道。此举更彻底地打破了国内盾…...
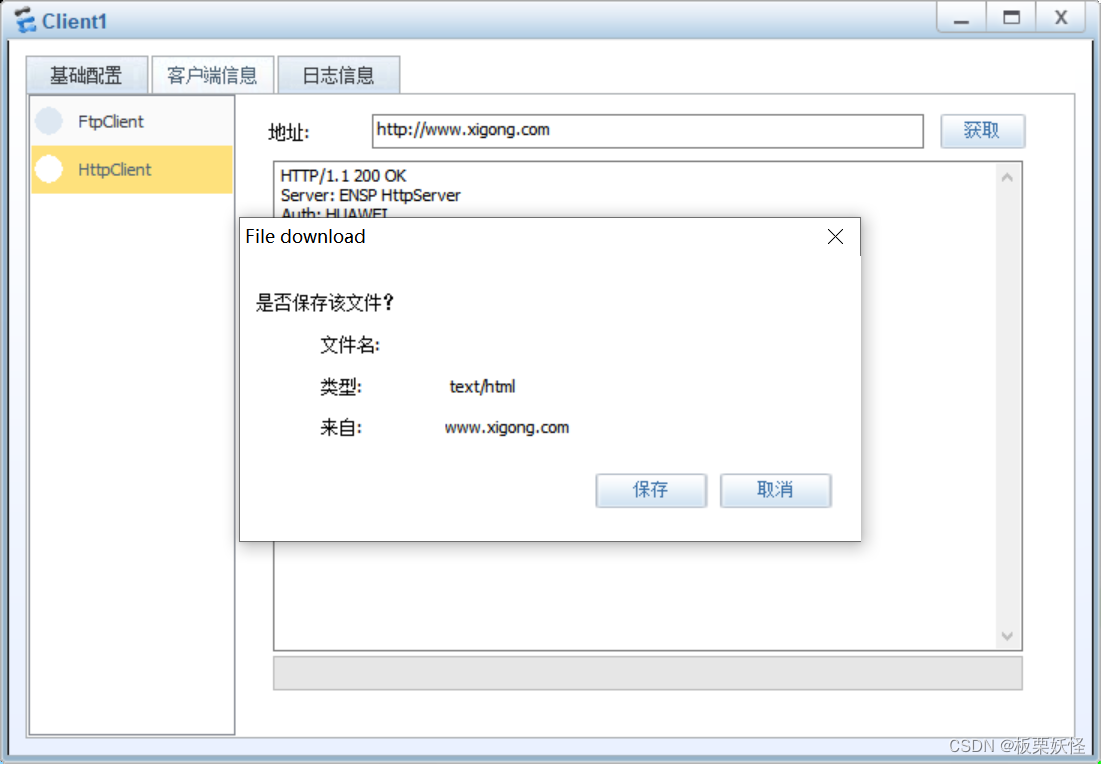
计算机网络课程设计-企业网三层架构
(单人版) 摘 要 本篇报告主要解决了为一家名为西宫的公司网络搭建问题,该网络采用企业网三层架构对完了过进行设计。首先使用以太网中继,主要使用VLAN划分的技术来划定不同部门。使用MSTP对每个组配置生成树,防止交换机…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...

第22节 Node.js JXcore 打包
Node.js是一个开放源代码、跨平台的、用于服务器端和网络应用的运行环境。 JXcore是一个支持多线程的 Node.js 发行版本,基本不需要对你现有的代码做任何改动就可以直接线程安全地以多线程运行。 本文主要介绍JXcore的打包功能。 JXcore 安装 下载JXcore安装包&a…...
