【算法专题】递归算法
递归
- 递归
- 1. 汉诺塔问题
- 2. 合并两个有序链表
- 3. 反转链表
- 4. 两两交换链表中的节点
- 5. Pow(x, n) --- 快速幂
递归
在解决⼀个规模为 n 的问题时,如果满足以下条件,我们可以使用递归来解决:
- 问题可以被划分为规模更小的子问题,并且这些子问题具有与原问题相同的解决⽅法。
- 当我们知道规模更小的子问题(规模为 n - 1)的解时,我们可以直接计算出规模为 n 的问题的解。
- 存在⼀种简单情况,或者说当问题的规模足够小时,我们可以直接求解问题。⼀般的递归求解过程如下:
a. 验证是否满足简单情况。
b. 假设较小规模的问题已经解决,解决当前问题
1. 汉诺塔问题
题目链接 -> Leetcode 面试题 08.06.汉诺塔问题
Leetcode 面试题 08.06.汉诺塔问题
题目:在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例1 :
输入:A = [2, 1, 0], B = [], C = []
输出:C = [2, 1, 0]
示例2 :
输入:A = [1, 0], B = [], C = []
输出:C = [1, 0]
提示 :
- A中盘子的数目不大于14个。
思路:
这是一道递归方法的经典题目,我们可以先从最简单的情况考虑:
- 假设 n = 1,只有⼀个盘子,很简单,直接把它从 A 中拿出来,移到 C 上;
- 如果 n = 2 呢?这时候我们就要借助 B 了,因为小盘子必须时刻都在大盘子上面,共需要 3 步(为了方便叙述,记 A 中的盘子从上到下为 1 号,2 号):
a. 1 号盘子放到 B 上;
b. 2 号盘子放到 C 上;
c. 1 号盘子放到 C 上。
至此,C 中的盘子从上到下为 1 号, 2 号 - 如果 n > 2 呢?这是我们需要用到 n = 2 时的策略,将 A 上面的两个盘子挪到 B 上,再将最大的盘子挪到 C 上,最后将 B 上的小盘子挪到 C 上就完成了所有步骤。
因为 A 中最后处理的是最大的盘子,所以在移动过程中不存在大盘子在小盘子上面的情况。
则本题可以被解释为:
- 对于规模为 n 的问题,我们需要将 A 柱上的 n 个盘子移动到C柱上。
- 规模为 n 的问题可以被拆分为规模为 n-1 的子问题:
a. 将 A 柱上的上面 n-1 个盘子移动到B柱上。
b. 将 A 柱上的最大盘子移动到 C 柱上,然后将 B 柱上的 n-1 个盘子移动到C柱上。 - 当问题的规模变为 n=1 时,即只有一个盘子时,我们可以直接将其从 A 柱移动到 C 柱。
- 需要注意的是,步骤 2.b 考虑的是总体问题中的子问题 b 情况。在处理子问题的子问题 b 时,我们应该将 A 柱中的最上面的盘子移动到 C 柱,然后再将 B 柱上的盘子移动到 C 柱。在处理总体问题的子问题 b 时,A 柱中的最大盘子仍然是最上面的盘子,因此这种做法是通用的。
代码如下:
class Solution {public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) { // 将 A 上的 A.size() 个盘子借助 B 移到 C 上dfs(A, B, C, A.size());}void dfs(vector<int>& A, vector<int>& B, vector<int>& C, int n){// 递归出口if(n == 1){C.push_back(A.back());A.pop_back();return;}// 将 A 上的 n - 1 个盘子借助 C 移到 B 上dfs(A, C, B, n - 1);C.push_back(A.back());A.pop_back();// 将 B 上的 n - 1 个盘子借助 A 移到 C 上dfs(B, A, C, n - 1);}};
2. 合并两个有序链表
题目链接 - > Leetcode -21.合并两个有序链表
Leetcode -21.合并两个有序链表
题目:将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
输入:l1 = [1, 2, 4], l2 = [1, 3, 4]
输出:[1, 1, 2, 3, 4, 4]
示例 2:
输入:l1 = [], l2 = []
输出:[]
示例 3:
输入:l1 = [], l2 = [0]
输出:[0]
提示:
- 两个链表的节点数目范围是[0, 50]
- 100 <= Node.val <= 100
- l1 和 l2 均按 非递减顺序 排列
思路:
- 递归函数的含义:交给你两个链表的头结点,把它们合并起来,并且返回合并后的头结点;
- 函数体:选择两个头结点中较小的结点作为最终合并后的头结点,然后将剩下的链表交给递归函数去处理;
- 递归出口:当某一个链表为空的时候,返回另外一个链表。
代码如下:
class Solution {public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if(list1 == nullptr) return list2;if(list2 == nullptr) return list1;if(list1->val < list2->val) {list1->next = mergeTwoLists(list1->next, list2);return list1;}else {list2->next = mergeTwoLists(list1, list2->next);return list2;}}};
3. 反转链表
题目链接 -> Leetcode -206.反转链表
Leetcode -206.反转链表
题目:给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
输入:head = [1, 2, 3, 4, 5]
输出:[5, 4, 3, 2, 1]
示例 2:
输入:head = [1, 2]
输出:[2, 1]
示例 3:
输入:head = []
输出:[]
提示:
- 链表中节点的数目范围是[0, 5000]
- 5000 <= Node.val <= 5000
思路:
- 递归函数的含义:交给你一个链表的头指针,逆序之后,返回逆序后的头结点;
- 函数体:先把当前结点之后的链表逆序,逆序完之后,把当前结点添加到逆序后的链表后面即可;
- 递归出口:当前结点为空或者当前只有一个结点的时候,不用逆序,直接返回。
代码如下:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/class Solution {public: ListNode* reverseList(ListNode* head) {if(head == nullptr || head->next == nullptr) return head;ListNode* ret = reverseList(head->next);head->next->next = head;head->next = nullptr;return ret;}};
4. 两两交换链表中的节点
题目链接 -> Leetcode -24.两两交换链表中的节点
Leetcode -24.两两交换链表中的节点
题目:给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。
你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
输入:head = [1, 2, 3, 4]
输出:[2, 1, 4, 3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
提示:
- 链表中节点的数目在范围[0, 100] 内
- 0 <= Node.val <= 100
思路:
- 递归函数的含义:交给你一个链表,将这个链表两两交换一下,然后返回交换后的头结点;
- 函数体:先去处理一下第二个结点往后的链表,然后再把当前的两个结点交换一下,连接上后面处理后的链表;
- 递归出口:当前结点为空或者当前只有一个结点的时候,不用交换,直接返回。
代码如下:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/class Solution {public:ListNode* swapPairs(ListNode* head){if (head == nullptr || head->next == nullptr) return head;ListNode* tmp = swapPairs(head->next->next);ListNode* ret = head->next; // 先存一下返回的头节点head->next->next = head;head->next = tmp;return ret;}};
5. Pow(x, n) — 快速幂
题目链接 -> Leetcode -50.Pow(x, n)
Leetcode -50.Pow(x, n)
题目:实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。
示例 1:
输入:x = 2.00000, n = 10
输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3
输出:9.26100
示例 3:
输入:x = 2.00000, n = -2
输出:0.25000
解释:2 - 2 = 1 / 22 = 1 / 4 = 0.25
提示:
- 100.0 < x < 100.0
- 2^31 <= n <= 2^31 - 1
- n 是一个整数
- 要么 x 不为零,要么 n > 0 。
- -10^4 <= x^n <= 10^4
思路:
- 递归函数的含义:求出 x 的 n 次方是多少,然后返回;
- 函数体:先求出 x 的 n / 2 次方是多少,然后根据 n 的奇偶,得出 x 的 n 次方是多少;
- 递归出口:当 n 为 0 的时候,返回 1 即可。
代码如下:
class Solution {public:// 2^10 = 2^5 * 2^5 = (2^2 * 2^2 * 2) * (2^2 * 2^2 * 2) = ...double _pow(double x, int n) {if(n == 0) return 1.0;double tmp = _pow(x, n / 2);return n % 2 == 0? tmp * tmp : tmp * tmp * x;}double myPow(double x, int n){return n >= 0? _pow(x, n) : 1.0 / _pow(x, abs(n));}};
相关文章:

【算法专题】递归算法
递归 递归1. 汉诺塔问题2. 合并两个有序链表3. 反转链表4. 两两交换链表中的节点5. Pow(x, n) --- 快速幂 递归 在解决⼀个规模为 n 的问题时,如果满足以下条件,我们可以使用递归来解决: 问题可以被划分为规模更小的子问题,并且…...

不停止业务的情况下优化 Elasticsearch Reindex
在使用 Elasticsearch 时,我们总有需要修改索引映射的时候,这时我们只能进行 _reindex。事实上,这是一个相当昂贵的操作,因为根据数据量和分片数量,完整复制一个索引可能需要几个小时。 花费的时间不是大问题,但更严重的是,它会影响生产环境的性能甚至功能。 相信大家…...

PB 按Excel动态创建对应字段
/* > Function: w_cwjk_xhyy.wf_dw_init >-------------------------------------------------------------------- > 描述: 按excel表格列名,创建对应字段,用于部分接口对应字段导出文件 >-------------------------------------------------------------------- …...
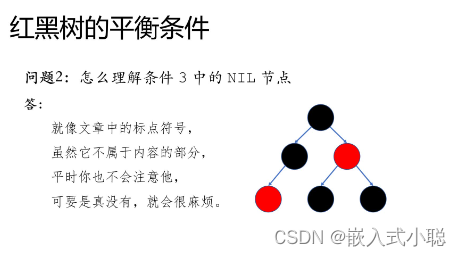
数据结构——红黑树 and B-树
红黑树 根据平衡条件第4、5两点 最短路径,都是黑色 最长路径,红黑相间 最长是最短的两倍 B-树...

Android中线程间的通信-Handler
Handler机制在Android中主要用于线程间的通信,特别是处理从子线程向主线程(UI线程)传递消息和更新界面。 Handler中的四个关键对象及其作用: Message: Message 是在线程间传递的数据载体,它包含了需要处理…...

Spring Boot Admin健康检查引起的Spring Boot服务假死
问题现象 最近在spring boot项目中引入了 spring-boot-starter-actuator 后,测试环境开始出现服务假死的现象, 且这个问题十分怪异,只在多个微服务中的简称A的这个服务中出现,其他服务都没有出现这个问题, 之所以说…...
java企业人事信息管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 java Web企业人事信息管理系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境 为TOMCAT7.0,Myeclipse8.5开发,数据库为M…...

如何通过 useMemo 和 useCallback 提升你的 React 应用性能
背景 在 React 中,useMemo 和 useCallback 这两个 hook 是我们优化应用性能的有力工具。它们会返回 memoized 版本的值或函数,只在依赖项发生变化时才进行重新计算或定义。 Hook 介绍 useMemo useMemo 的作用是返回一个 memoized 值,它接…...
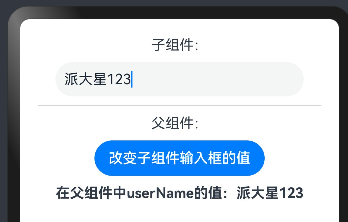
ArkTS - @Prop、@Link
一、作用 Prop 装饰器 和Link装饰器都是父组件向子组件传递参数,子组件接收父组件参数的时候用的,变量前边需要加上Prop或者Link装饰器即可。(跟前端vue中父组件向子组件传递参数类似) // 子组件 Component struct SonCom {Prop…...

Python中matplotlib库的使用1
1 matplotlib库简介 matplotlib是一个数学绘图库,可以将数据通过图形的方式显示出来,也就是数据可视化。 2 matplotlib库的安装 2.1 打开cmd窗口 点击键盘的“Win”“R”键,在弹出的“运行”对话框的“打开”栏中输入“cmd”,…...

位乘积计数-蓝桥
题目链接:1.位乘积计数 - 蓝桥云课 (lanqiao.cn) 解题思路:10的5次数量级暴力居然过了,看来测试样例很水,直接1遍历到n,再用一个循环判断每位数相乘乘机是否等于m即可。 下面是c代码: #include <iost…...

HCIA-Datacom题库(自己整理分类的)——OSPF协议判断
1.路由表中某条路由信息的Proto为OSPF则此路由的优先级一定为10。√ 2.如果网络管理员没有配置骨干区域,则路由器会自动创建骨干区域? 路由表中某条路由信息的Proto为OSPF,则此路由的优先级一定为10。 当两台OSPF路由器形成2-WAY邻居关系时࿰…...

【FPGA/verilog -入门学习16】fpga状态机实现
需求: 用两段式状态机设计序列码检测机。这个序列码检测机用于检索连续输入的 1bit 数据 (每个时钟周期输入 1bit),当检测到一串“101100”的输入数据时,产生一个时钟周期的 高脉冲指示信号 状态图 //实现状态机切…...
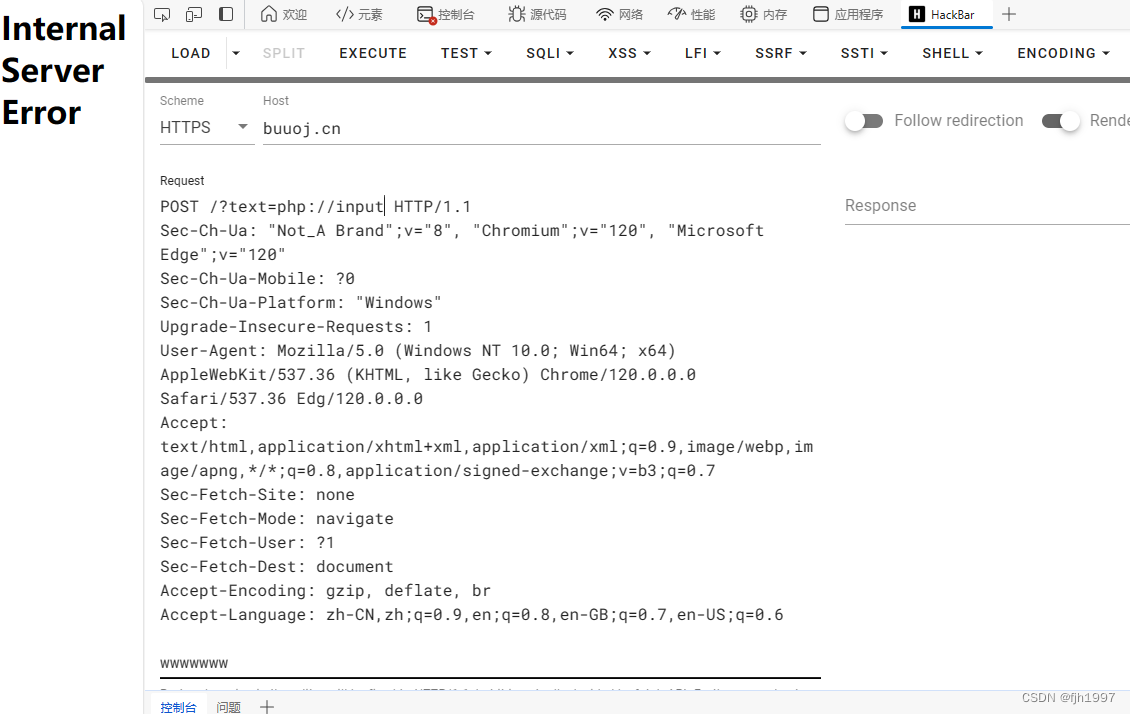
记chrome的hackbar无法post php://input的问题
尽管hackbar支持post请求体,但是当请求体里面没有等于号的时候,无法post出去,这样如果需要使用php://input绕过waf的时候就没法做。 在开发人员工具的网络里面可以看到不使用等于号的情况下没有荷载。 之后在这里看到了解决方法,…...

相机解析驱动小记
用过了几款相机,对使用相机也有了一点心得,在此记录。 当你得到一款相机,你需要做的: 第一件事:在datasheet中阅读配置单,知道怎么配置、配置完输出来是什么。 配置输出尺寸;传输模式…...

EasyExcel判断导入时是否符合给定模板
问题描述 在做系统的导入导出模块时需要在导入时判断用户导入的表格是否符合给定的模板,该系统导入导出使用的是EasyExcel,因此在实现该功能时是基于EasyExcel的 解决方案 创建Spring Boot项目,并添加如下依赖 <dependency><group…...

BDD - Python Behave Retry 机制
BDD - Python Behave Retry 机制 引言Behave RetryBehave Retry 应用feature 文件创建 step 文件Retry运行 Behave 并生成 rerun 文件重新运行失败的场景 引言 在日常运行测试用例,有时因为环境不稳定造成一些测试用例跑失败了,如果能将这些失败的测试用…...

链 表
3_1 删除链表中的节点 Answer-将被删节点下一个val复制到待删除节点,然后将待删节点直接连接到下下一个节点即可。 学到: /** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode(int x) …...

一个可以用于生产环境得PHP上传函数
上传表单 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><title>文件上传</title> </head> <body><h1>选择要上传的文件</h1><!-- 定义一个包含文件输入字段的表单 --…...

PyTorch中常用的工具(3)TensorBoard
文章目录 前言3 可视化工具3.1 TensorBoard 前言 在训练神经网络的过程中需要用到很多的工具,最重要的是数据处理、可视化和GPU加速。本章主要介绍PyTorch在这些方面常用的工具模块,合理使用这些工具可以极大地提高编程效率。 由于内容较多,…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...
智警杯备赛--excel模块
数据透视与图表制作 创建步骤 创建 1.在Excel的插入或者数据标签页下找到数据透视表的按钮 2.将数据放进“请选择单元格区域“中,点击确定 这是最终结果,但是由于环境启不了,这里用的是自己的excel,真实的环境中的excel根据实训…...
