收集最新的 Sci-Hub 网址（本文章持续更新2024）
自用收集最新的 Sci-Hub 网址
本文章持续更新收集 Sci-Hub 的可用网址链接仅供交流学习使用，如对您有所帮助，请收藏并推荐给需要的朋友，由于网站限制，不一定所有网址都能在您所在的位置访问，通常情况下，一半以上是有效的。
Sci-Hub是一个旨在免费获取学术论文的网站，由哈萨克斯坦的Alexandra
Elbakyan创建。这个网站提供了大量的科学论文，涵盖了多个学科领域，让用户可以免费获取通常需要付费或者需要订阅才能获得的学术文献。Sci-Hub使用了多种方式来获取论文，包括爬取学术期刊网站、获取用户分享的文献等。虽然Sci-Hub受到了一些争议，因为它绕过了一些付费订阅的机制，但它也受到了许多人的欢迎和支持。对于很多没有资源获取昂贵期刊订阅的人来说，Sci-Hub提供了一个重要的资源渠道，让他们能够获得所需的学术文献，这在某种程度上促进了科学知识的分享和传播。
所有可用链接都在文件，自行免费下载
本文章持续更新收集，有需要的朋友请自行收藏下载。
域名 状态
√ https://sci-hub.wf 可用
√ https://sci-hub.ee 可用
√ https://sci-hub.st 可用
√ https://sci-hub.yt 可用
√ https://sci-hub.se 可用
√ https://sci-hub.ru 可用
√ https://sci-hub.ren 可用
√ https://sci-hub.cat 可用
√ https://sci-hub.shop 可用
√ https://sci-hub.mobi 可用
√ https://sci-hub.click 可用
√ https://sci-hub.mksa.top 可用
√ https://sci-hub.et-fine.com 可用
√ https://sci-hub.hkvisa.net 可用
√ https://sci-hub.3800808.com 可用
√ https://scihub.unblockit.zip 可用
所有可用链接都在文件，自行免费下载
相关文章：
收集最新的 Sci-Hub 网址（本文章持续更新2024）
自用收集最新的 Sci-Hub 网址 本文章持续更新收集 Sci-Hub 的可用网址链接仅供交流学习使用，如对您有所帮助，请收藏并推荐给需要的朋友，由于网站限制，不一定所有网址都能在您所在的位置访问，通常情况下，一…...
针对NPC客户端的升级（脚本执行）
上一次我们使用NPS自动注册的方式，在被控端上实现了自动创建NPC客户端链接。 Linux主机自动注册NPS客户端（脚本化） 但是在使用过程中我发现存在很多的问题，如果被控端重启客户端或者出现了多个NPS时会造成冲突，所以考虑…...
[每周一更]-(第51期)：Go的调度器GMP
参考文献 https://learnku.com/articles/41728http://go.cyub.vip/gmp/gmp-model.html#g-m-phttps://blog.csdn.net/ByteDanceTech/article/details/129292683https://www.ququ123.top/2022/04/golang_gmp_principle/ 什么是GMP? GMP模型是Go语言并发模型的核心概念&#x…...
阿里云和腾讯云服务器系统盘40G或50G空间够用吗？
云服务器系统盘40G或50G空间够用吗？够用，操作系统一般占用几个GB的存储空间，尤其是Linux操作系统占用空间容量更小，阿里云和腾讯云服务器系统盘默认提供的40GB高效云盘或50G通用型SSD云硬盘，阿腾云atengyun.com分享是否…...
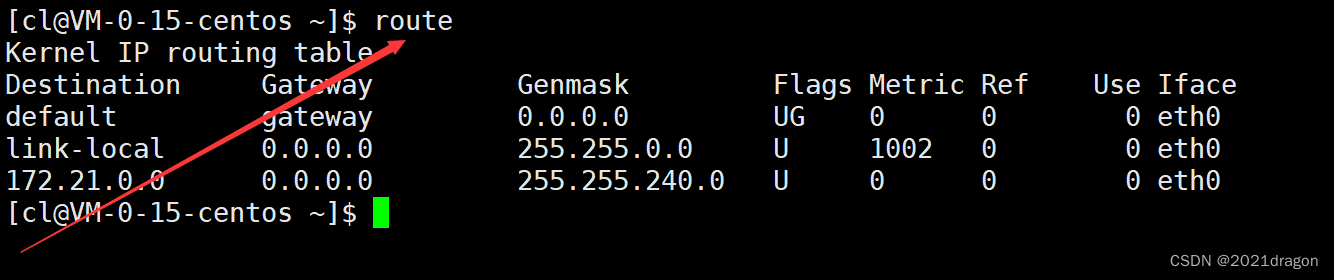
网络层协议 ——— IP协议
文章目录 IP协议基本概念IP协议格式分片与组装网段划分特殊的IP地址IP地址的数量限制私网IP地址和公网IP地址路由路由表生成算法 IP协议 IP协议全称为“网际互连协议（Internet Protocol）”，IP协议是TCP/IP体系中的网络层协议。 基本概念 网…...
函数的用法)
MATLAB --- interp1( )函数的用法
interp1() 是 MATLAB 中用于一维插值的函数， 它可以根据给定的数据点进行插值，从而在给定的插值点处估计函数的值 下面是 interp1() 函数的用法： Vq interp1(X, V, Xq) Vq interp1(X, V, Xq, method) Vq interp1(X, V, Xq, method, extr…...
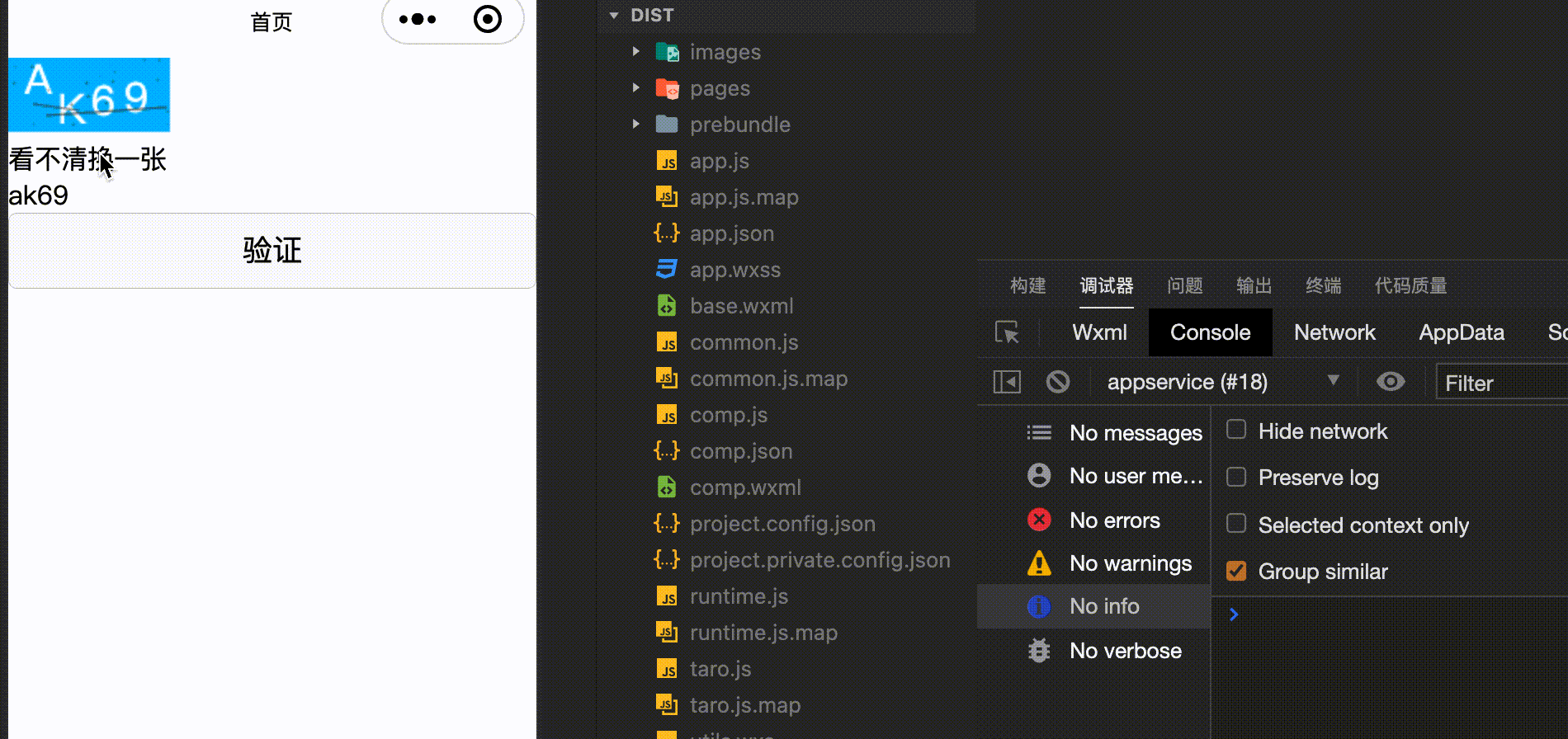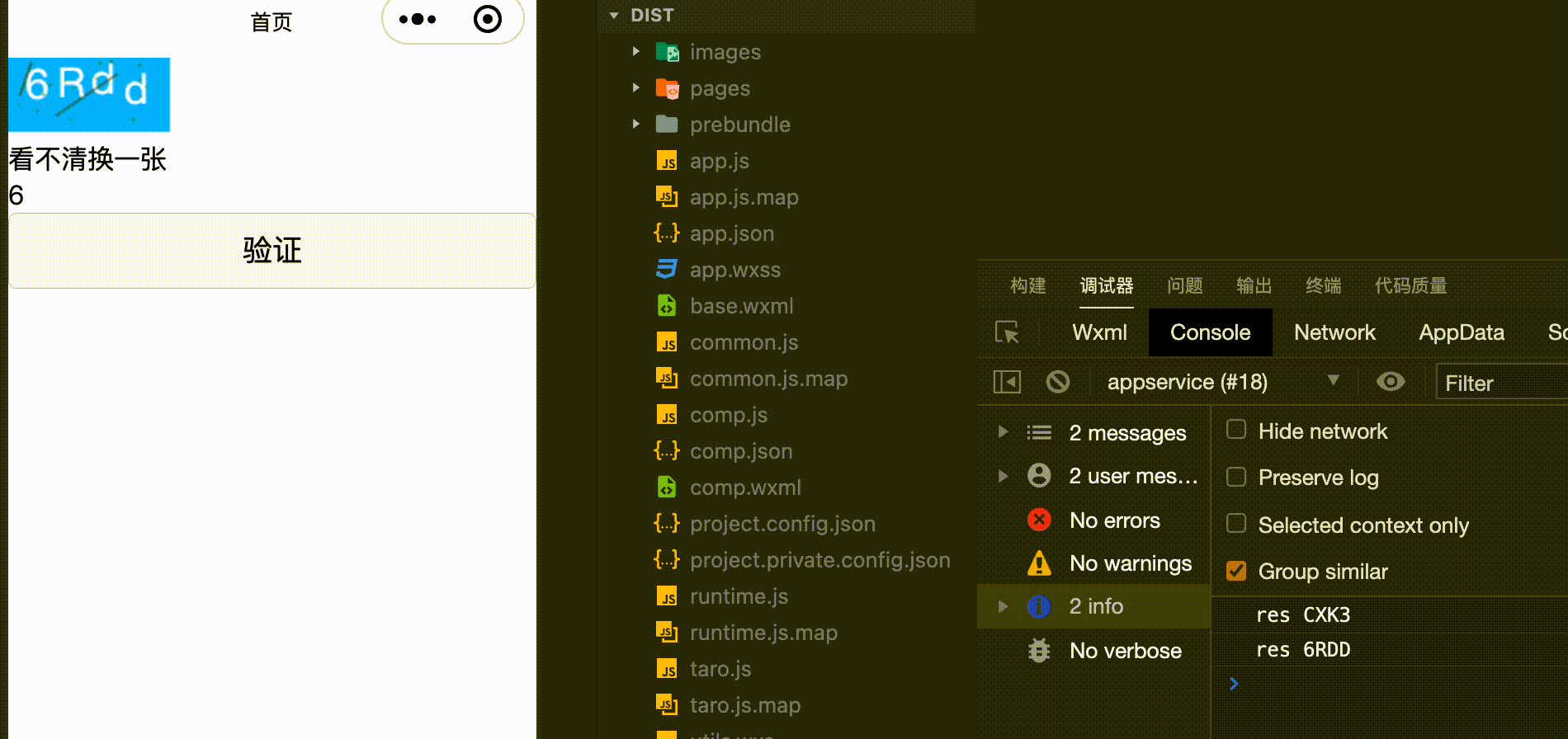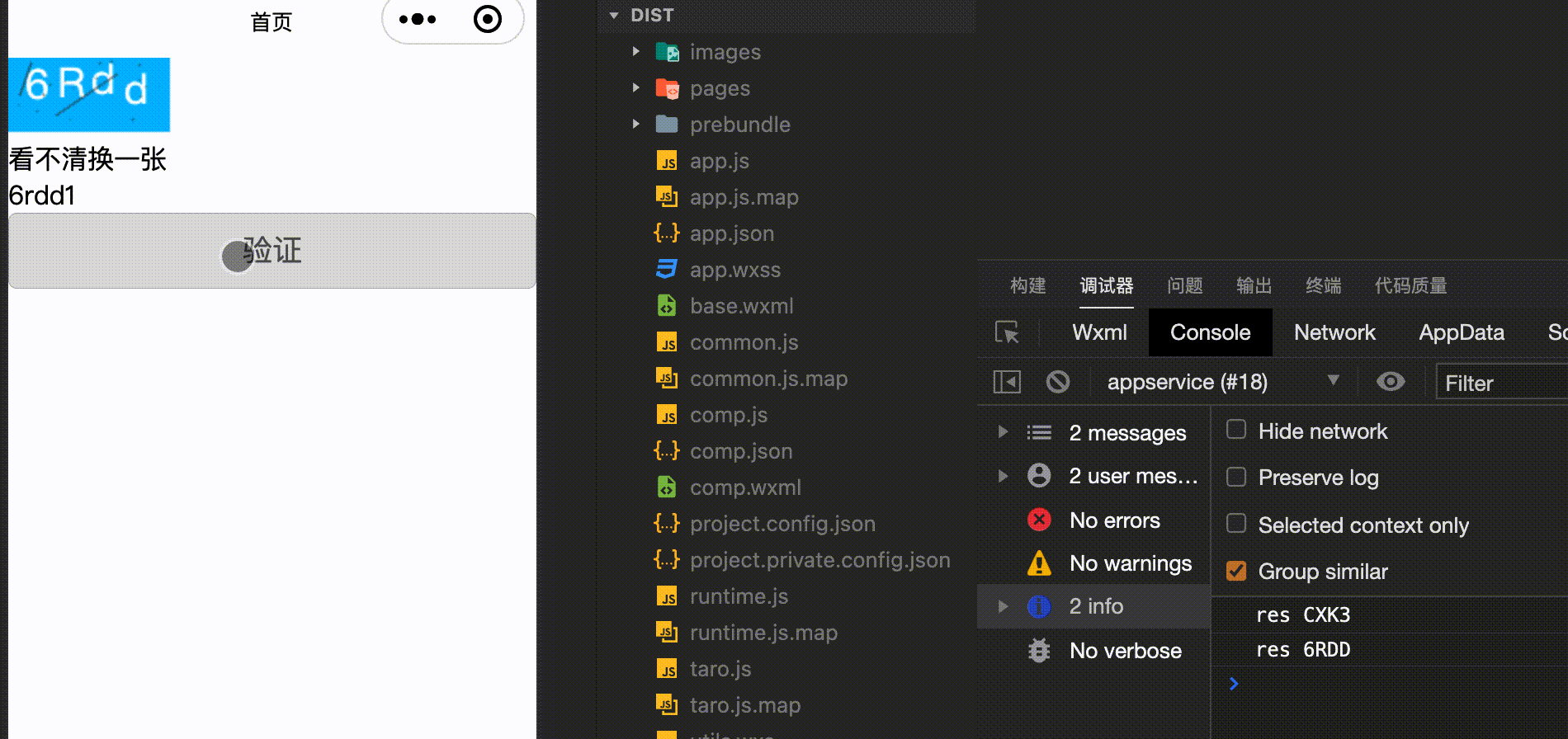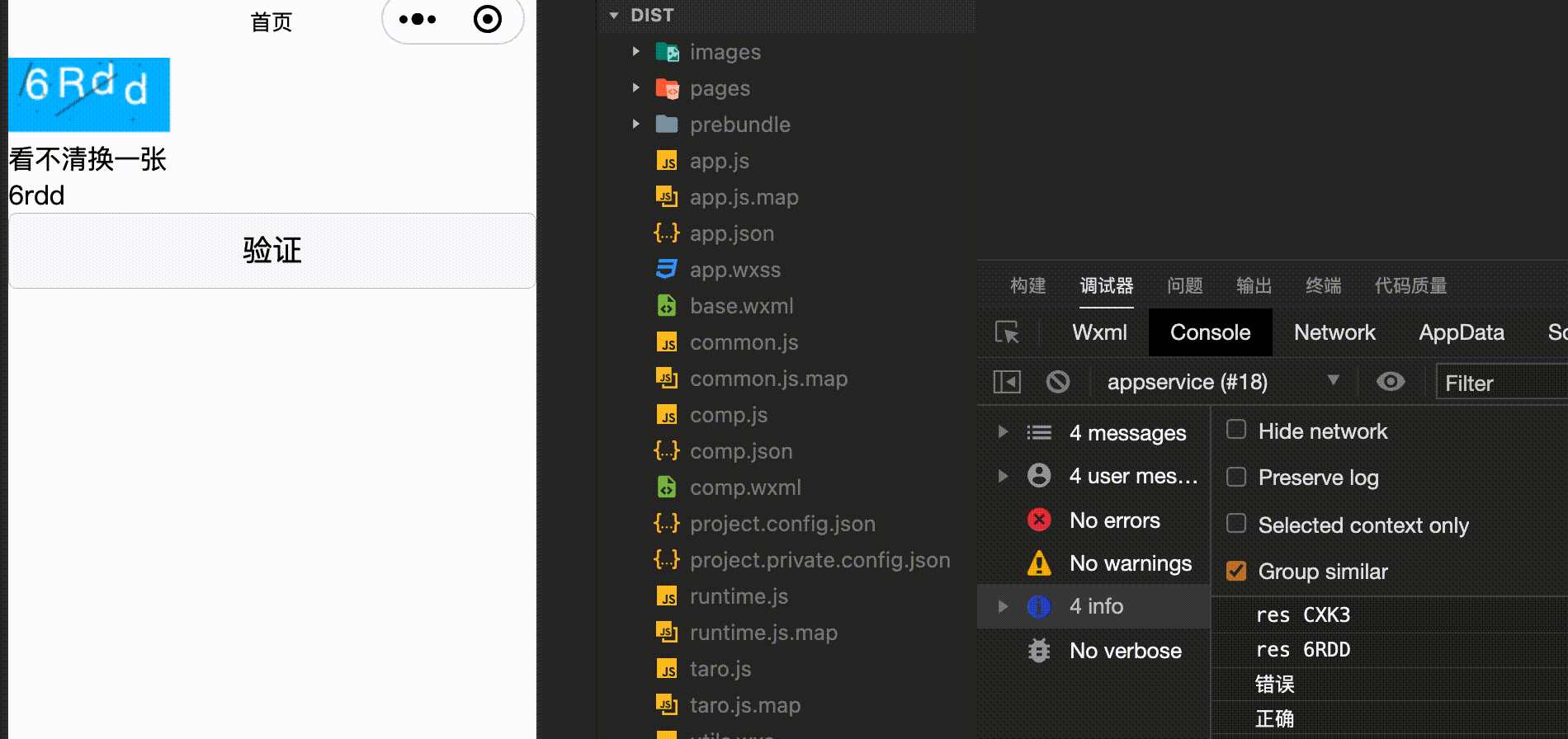
【react-taro-canvas】用canvas手写一个数字、字母混合的行为验证码
用canvas手写一个数字、字母混合的行为验证码 实现效果源码 实现效果 源码 import Taro from "tarojs/taro"; import { View, Canvas, Input, Button } from "tarojs/components"; import { useState, useEffect } from "react"; // 画随机线函…...
ctfshow——信息搜集
文章目录 web 1web 2web 3web 4web 5web 6web 7web 8web 9web 10web 11web 12web 13web 14web 15web 16web 17web 18web 19web 20 web 1 题目提示开发注释未及时删除。 直接右键查看源代码。 web 2 在这关我们会发现：1）无法使用右键查看源代码&…...
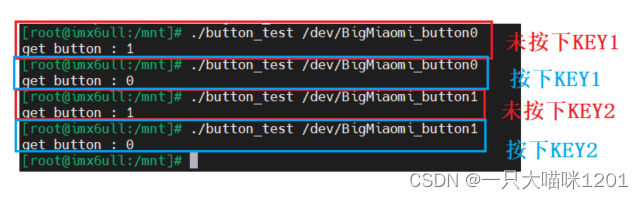
【Linux驱动】设备树模型的LED驱动 | 查询方式的按键驱动
🐱作者：一只大喵咪1201 🐱专栏：《Linux驱动》 🔥格言：你只管努力，剩下的交给时间！ 目录 🍮设备树模型的LED驱动🍩设备树文件🍩驱动程序 …...
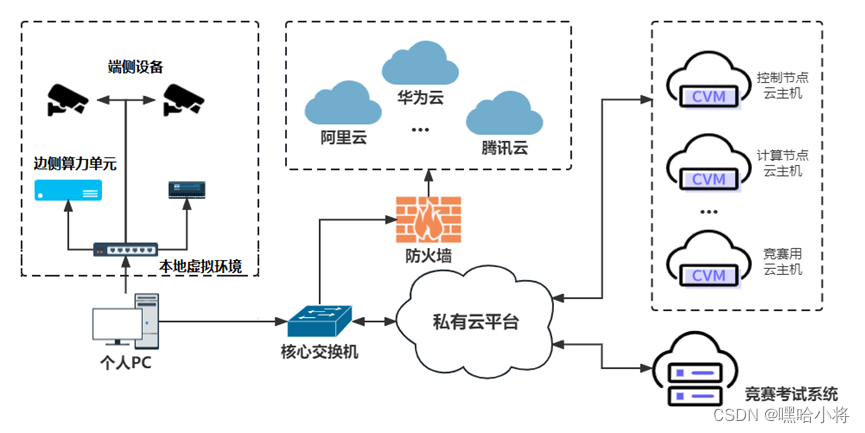
GZ075 云计算应用赛题第4套
2023年全国职业院校技能大赛（高职组） “云计算应用”赛项赛卷4 某企业根据自身业务需求，实施数字化转型，规划和建设数字化平台，平台聚焦“DevOps开发运维一体化”和“数据驱动产品开发”，拟采用开源OpenSt…...
小型肉制品厂废水处理设备加工厂家
诸城市鑫淼环保小编带大家了解一下小型肉制品厂废水处理设备加工厂家 在小型肉制品厂，处理肉类加工废水是非常重要的环保问题。废水中含有蛋白质、脂肪、悬浮物和有机物等，需要进行合适的处理以减少对环境的污染。以下是一些常见的小型肉制品厂废水处理设…...
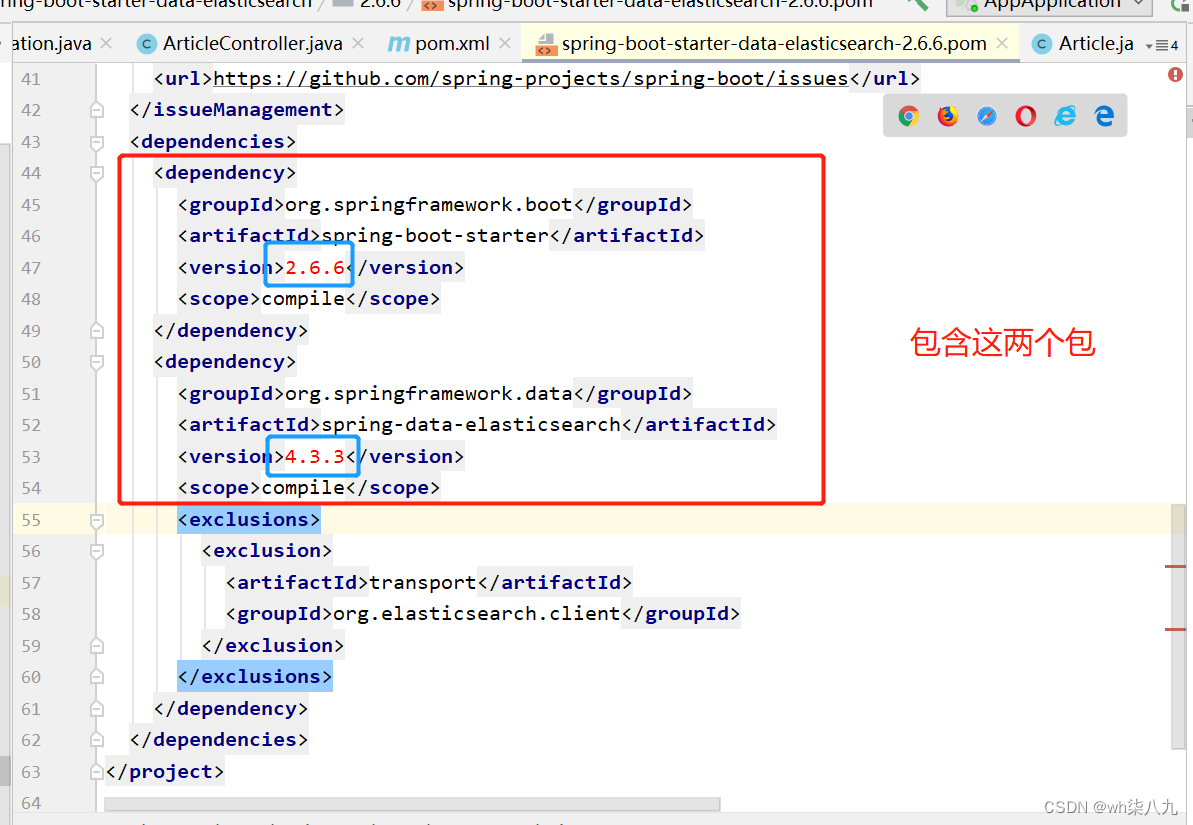
SpringBoot整合ElasticSearch实现CRUD操作
本文来说下SpringBoot整合ES实现CRUD操作 文章目录 概述项目搭建ES简单的crud操作本文小结 概述 SpringBoot支持两种技术和es交互。一种的jest，还有一种就是SpringData-ElasticSearch。根据引入的依赖不同而选择不同的技术。反正作为spring全家桶，目前是…...
香橙派--关于jammy-xfce-arm64.f12a43b3e629442a073a7236bf9166ce.tar.lz4的rootfs定制与镜像制作
使用 x64 的 Ubuntu22.04 电脑编译 Linux SDK，即 orangepi-build，支持在安装有 Ubuntu 22.04 的电脑上运行，所以下载 orangepi-build 前，请首先确保自己电脑已安装的 Ubuntu 版本是 Ubuntu22.04。查看电脑已安装的 Ubuntu 版本的命…...
前端八股文（HTML篇）一
目录 1.什么是DOCTYPE,有何用呢？ 2.说说对html语义化的理解 3.src和href的区别？ 4.title与h1的区别，b与strong的区别，i与em的区别？ 5.什么是严格模式与混杂模式？ 6.前端页面有哪三层构成，分…...
数据结构与算法python版本之线性结构之无序表抽象数据类型有序链表抽象数据类型和总结
我们知道，列表List是一种简单强大的数据集结构，提供了丰富的操作接口；但是并不是所有的编程语言都提供了List数据类型，有时候需要程序员自己实现。 那么什么是列表呐？ 列表是一种数据项按照相对位置存放的数据集&…...
识别pdf中论文标题并重命名PDF名称（2024.1.2，第二次更新）判断标题中是否以空格结尾
63~66行增加语句，判断标题是否以空格结尾 83~85行增加语句，判断选句是否以空格结尾 import os import timeimport fitzdef find_largest_font_sentence(pdf_path):largest_font_size 0largest_font_sentence maxsize0# 打开PDF文件document fitz.ope…...
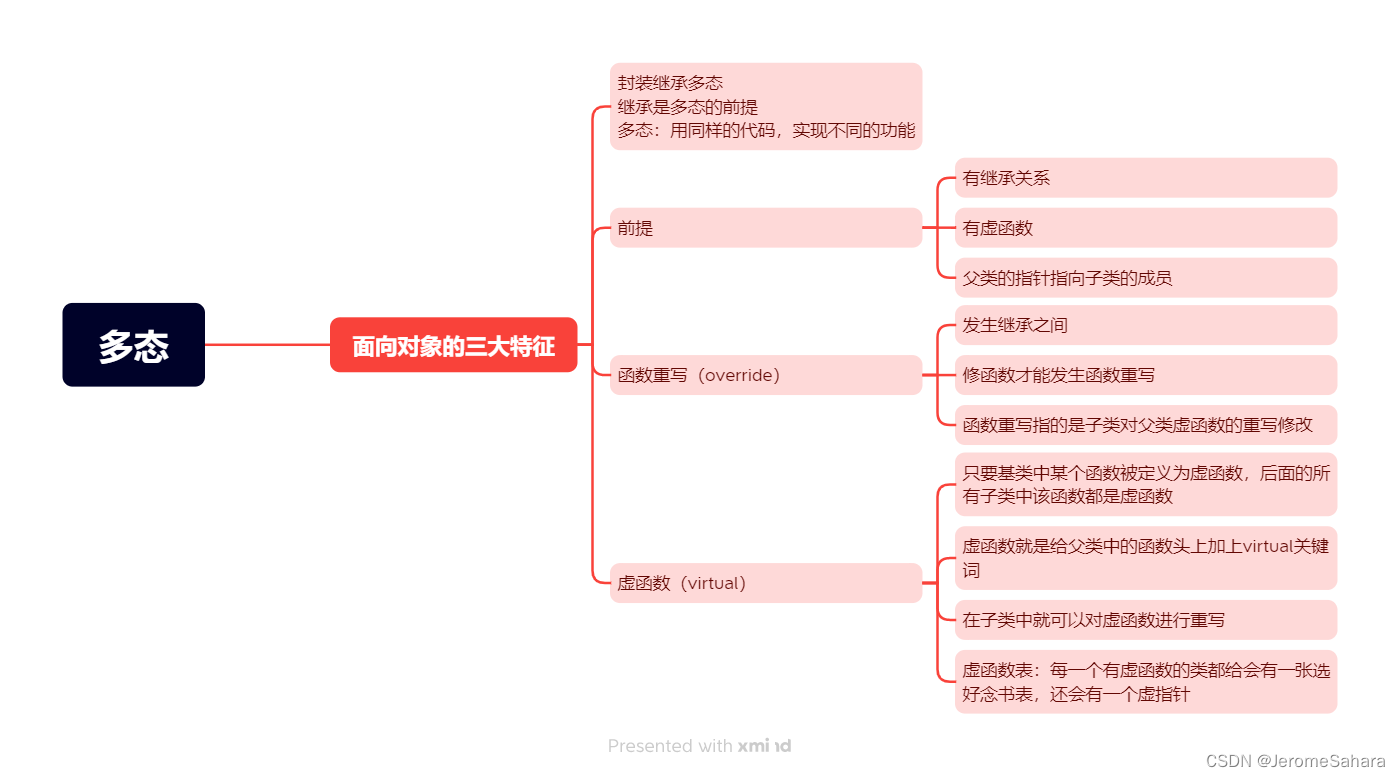
01.02作业
整理思维导图复习课上代码全局变量，int monster 10000;定义英雄类hero，受保护的属性string name，int hp,int attck；公有的无参构造，有参构造，虚成员函数 void Atk(){blood-0;}，法师类继承自英雄…...
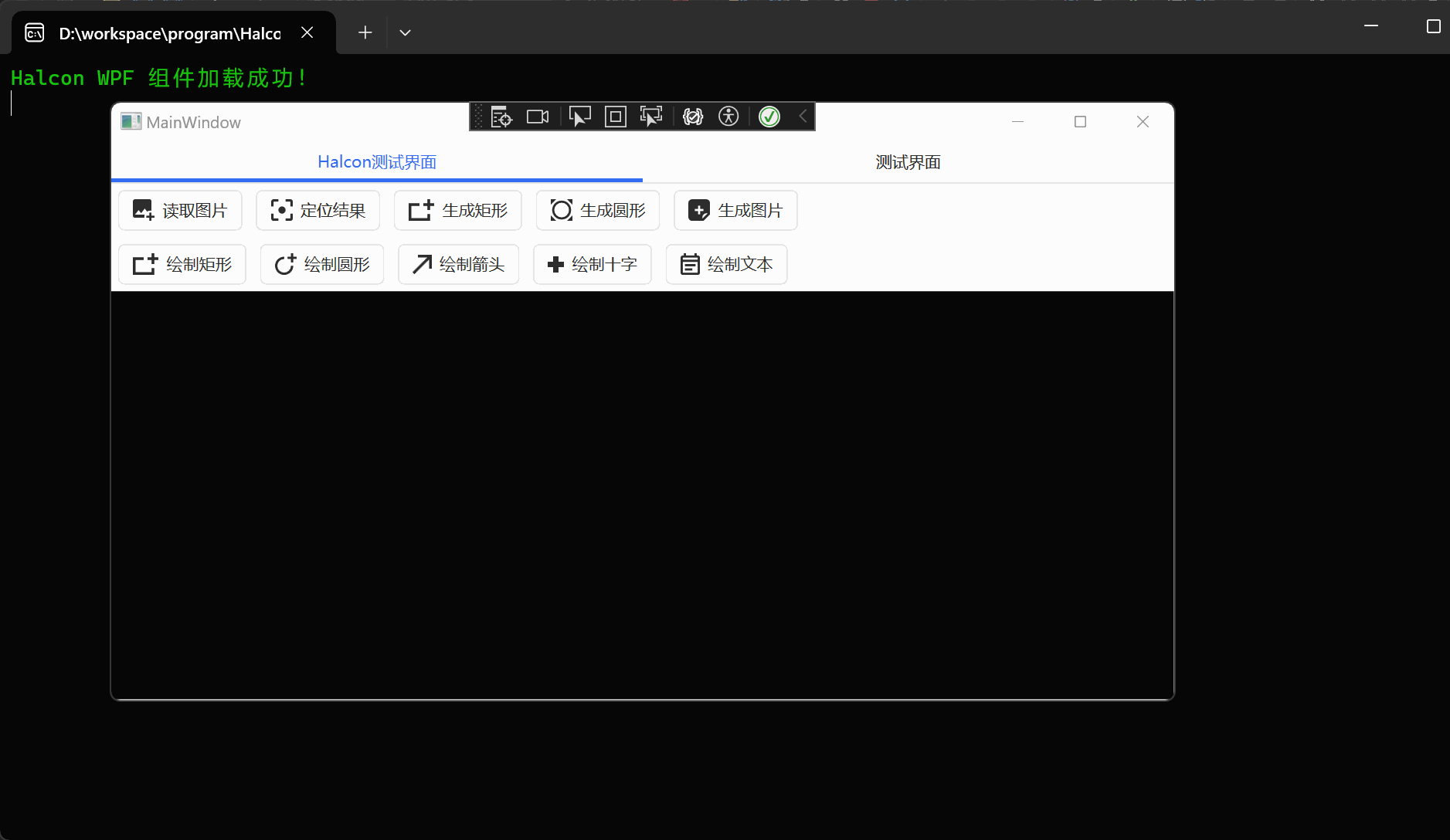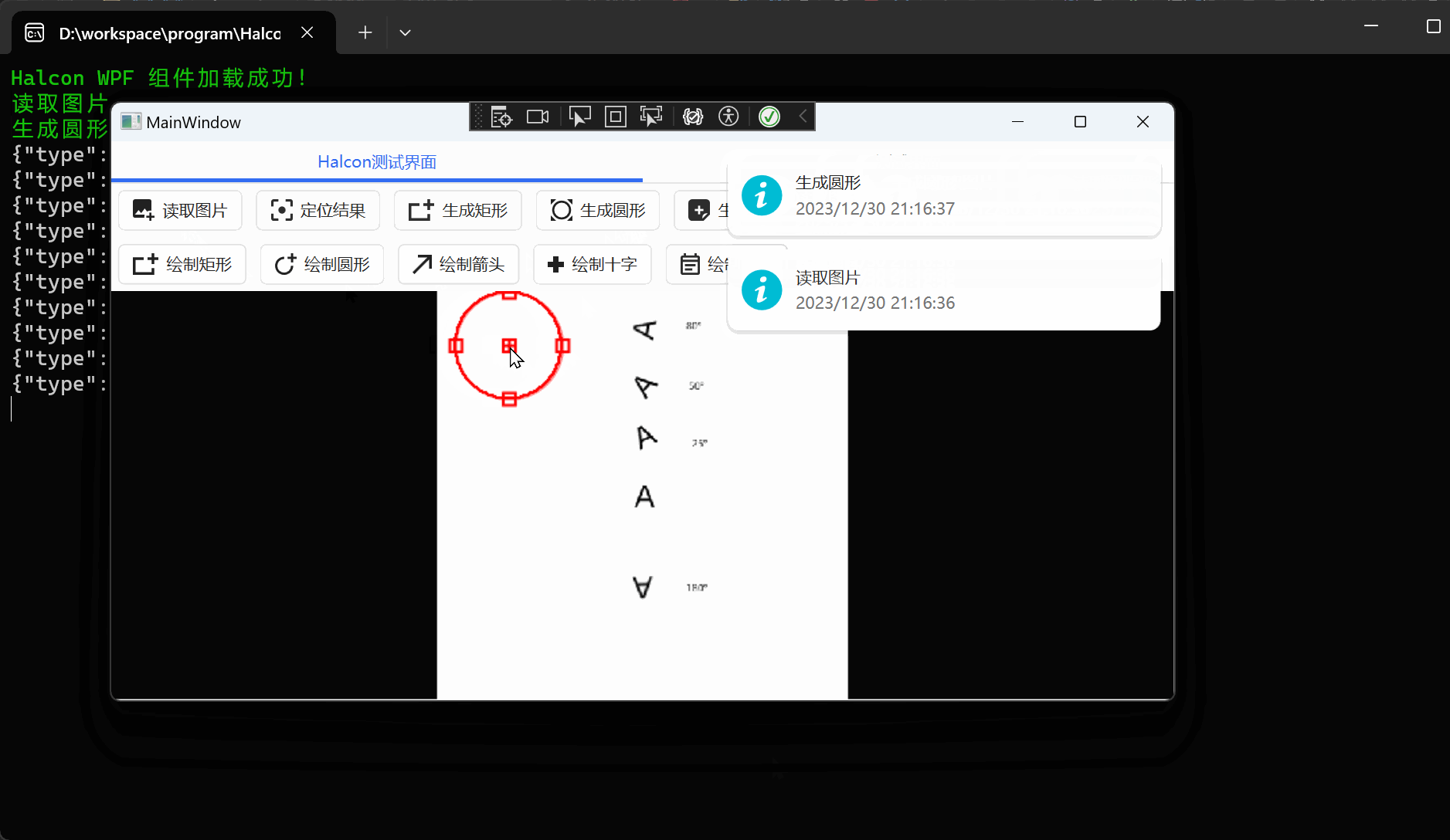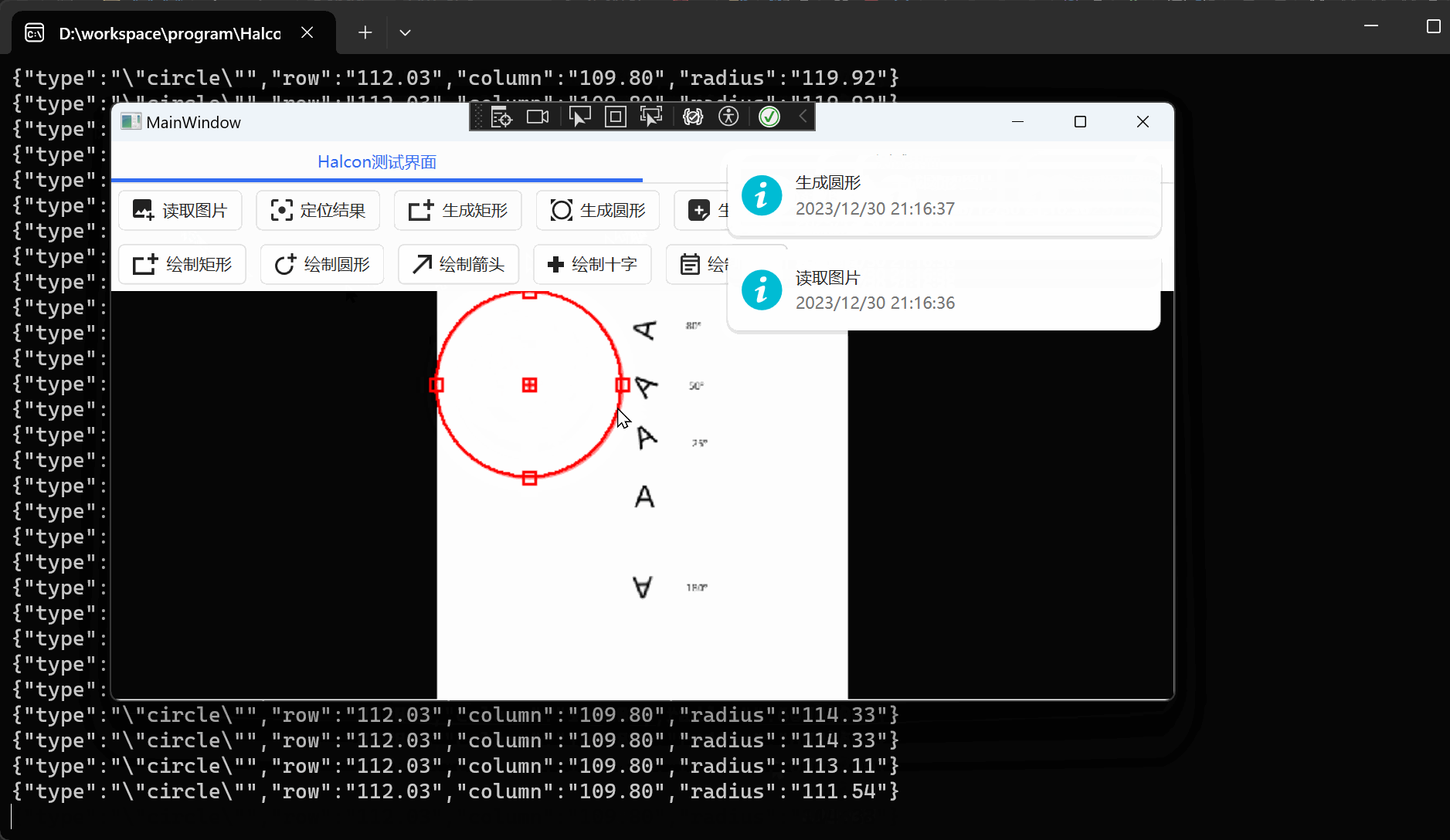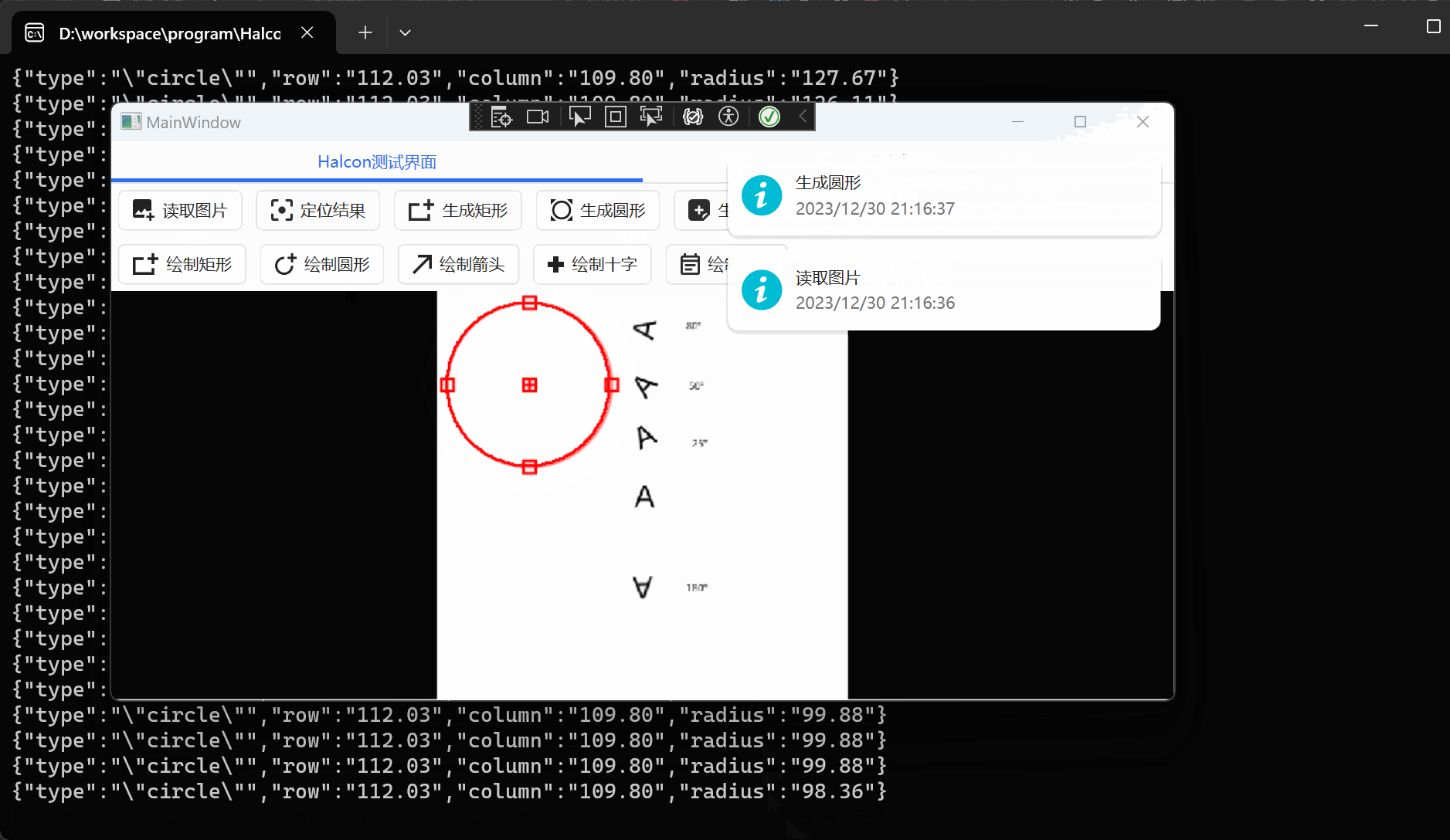
WPF+Halcon 培训项目实战(11):HS组件封装
文章目录 前言相关链接项目专栏运行环境匹配图片封装组件新增类库项目选择依赖顺序并添加Nuget修改原本矩形方法运行结果： 对矩形进行抽象封装抽象基类矩形抽象改造 圆形抽象封装代码运行结果 前言 为了更好地去学习WPFHalcon，我决定去报个班学一下。原…...
VUE——IDEA 启动前端工程VS文件启动前端工程
IDEA 启动前端 目录 前言一、打开控制台二、输入npm install三、依赖下载完之后，输入npm run dev，运行前端项目1、IDEA启动前端工程2、文件目录启动前端工程 四、点击http://localhost:8080后续敬请期待 前言 启动已有的vue前端项目 一、打开控制台 选…...
自动驾驶论文
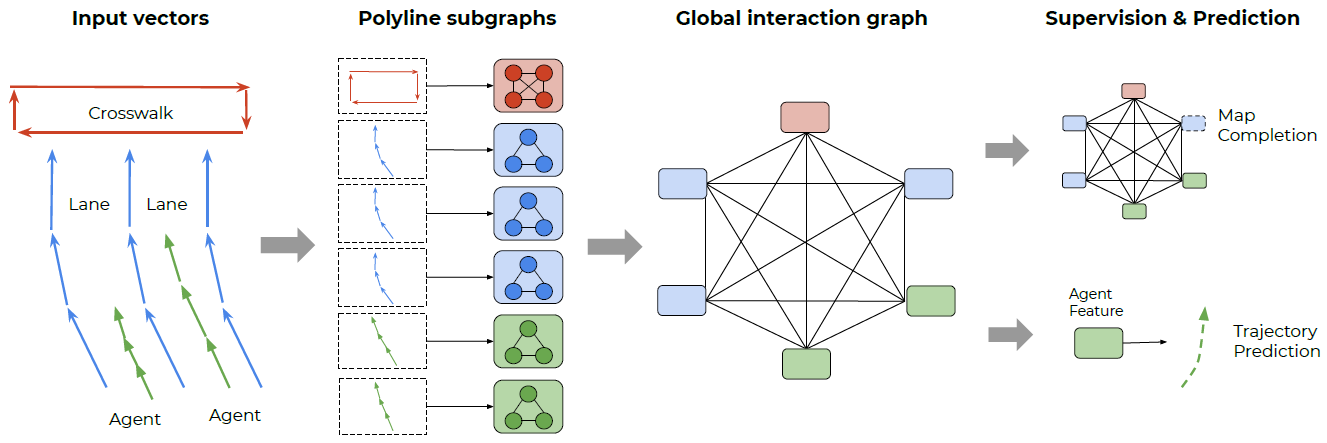
文章目录 一、Convolutional Social Pooling for Vehicle Trajectory Prediction二、QCNet：Query-Centric Trajectory Prediction三、VectorNet: Encoding HD Maps and Agent Dynamics from Vectorized Representation 一、Convolutional Social Pooling for Vehicl…...
golang循环变量捕获问题
在 Go 语言中，当在循环中启动协程（goroutine）时，如果在协程闭包中直接引用循环变量，可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下： 问题背景 看这个代码片段： fo…...
2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议（EPSFD 2025）将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会，EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...
大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动（如演唱会、马拉松赛事、高考中考等）期间，城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例，暖城商圈曾因观众集中离场导致周边…...
新能源汽车智慧充电桩管理方案：新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及，充电桩作为核心配套设施，其安全性与可靠性备受关注。然而，在高温、高负荷运行环境下，充电桩的散热问题与消防安全隐患日益凸显，成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言，以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天，异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX（不访问内存）XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中，提示一个依赖外部头文件的cpp源文件需要同步，点…...
在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的？
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件，用于在原生应用中加载 HTML 页面： 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件，或者在构建过程中仍然引用了旧的路…...