树状数组讲解
树状数组
文章目录
- 树状数组
- 引入
- 例题
- AcWing241.楼兰图腾
- 思路
- 代码
- AcWing 242. 一个简单的整数问题
- 思路
- 代码
- AcWing 244. 谜一样的牛
- 思路
- 代码
- 总结
引入
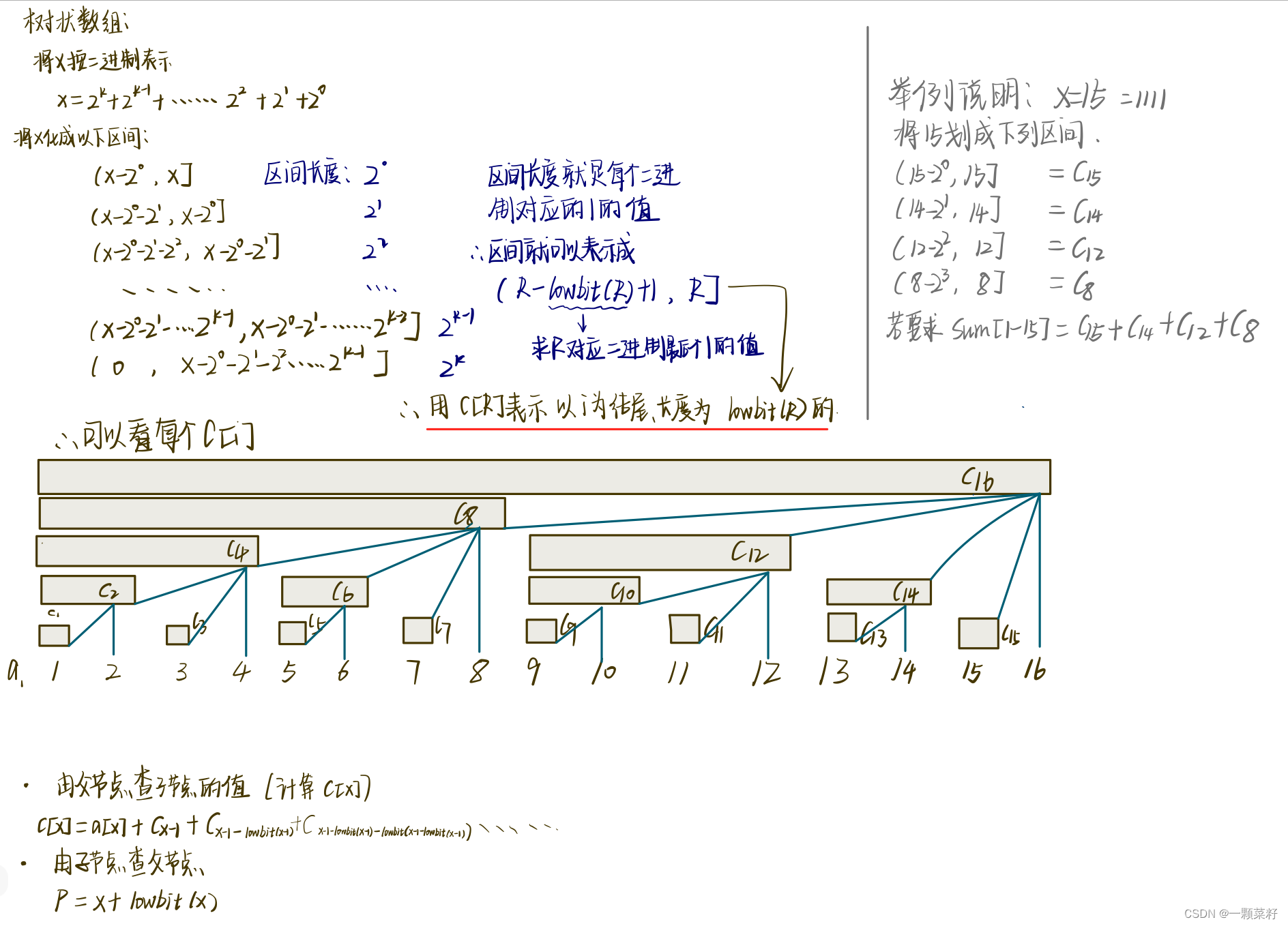
树状数组主要维护的是这样一个数据结构:
tr[x]表示以x为终点的长度为lowbit(x)的前缀和、最大值、最小值、最大公约数
对于树状数组主要就两种操作
- 对一段区间求和、求最值、求最大公约数,这里以求和为例。
通过合并分解后的每一段长度为相应lowbit的tr[i]求解
模板
def ask(x) :res = 0i = xwhile i :res += tr[i]i -= lowbit(i)return res
- 修改某个数
通过对其每一段父节点(加上lowbit)进行操作。
def add(x, c) :i = xwhile i <= n :tr[i] += ci += lowbit(i)
应用:
例题
AcWing241.楼兰图腾
在完成了分配任务之后,西部 314
来到了楼兰古城的西部。
相传很久以前这片土地上(比楼兰古城还早)生活着两个部落,一个部落崇拜尖刀(V),一个部落崇拜铁锹(∧),他们分别用 V 和 ∧ 的形状来代表各自部落的图腾。
西部 314
在楼兰古城的下面发现了一幅巨大的壁画,壁画上被标记出了 n
个点,经测量发现这 n
个点的水平位置和竖直位置是两两不同的。
西部 314
认为这幅壁画所包含的信息与这 n
个点的相对位置有关,因此不妨设坐标分别为 (1,y1),(2,y2),…,(n,yn)
,其中 y1∼yn
是 1
到 n
的一个排列。
西部 314
打算研究这幅壁画中包含着多少个图腾。
如果三个点 (i,yi),(j,yj),(k,yk)
满足 1≤i<j<k≤n
且 yi>yj,yj<yk
,则称这三个点构成 V 图腾;
如果三个点 (i,yi),(j,yj),(k,yk)
满足 1≤i<j<k≤n
且 yi<yj,yj>yk
,则称这三个点构成 ∧ 图腾;
西部 314
想知道,这 n
个点中两个部落图腾的数目。
因此,你需要编写一个程序来求出 V 的个数和 ∧ 的个数。
输入格式
第一行一个数 n
。
第二行是 n
个数,分别代表 y1,y2,…,yn
。
输出格式
两个数,中间用空格隔开,依次为 V 的个数和 ∧ 的个数。
数据范围
对于所有数据,n≤200000
,且输出答案不会超过 int64
。
y1∼yn
是 1
到 n
的一个排列。
输入样例:
5
1 5 3 2 4
输出样例:
3 4
思路
对于V形图腾来说,可以通过枚举每一个点作为最低点时,可组成的V形序列个数,最终求和得到最终答案。
基于单个点x,我们可以先从左到右的记录其左端大于x的点个数,同理可以记录其右端大于x的点个数,二者相乘即为结果。
每次都得查询之前所有点中小于(大于)a[x]的个数,再遍历后一个点前,需要将当前点加入查询的数据结构中。
区间查询、单点修改
树状数组呼之欲出。
代码
N = 200010
a = [0] * Ndef lowbit(x) :return x & -xdef ask(x) :res = 0i = xwhile i :res += tr[i]i -= lowbit(i)return resdef add(x, c) :i = xwhile i <= n :tr[i] += ci += lowbit(i)n = int(input())
a[1 : n + 1] = list(map(int, input().split()))greater, lower = [0] * (n + 1), [0] * (n + 1)
tr = [0] * (n + 1)
# 从左到右,记录每个点左边大于/小于的情况
for i in range(1, n + 1) :x = a[i]greater[i] = ask(n) - ask(x)lower[i] = ask(x - 1)add(x, 1)res1, res2 = 0, 0
tr = [0] * (n + 1)
# 从右到左求解结果
for i in range(n, 0, -1) :x = a[i]res1 += greater[i] * (ask(n) - ask(x))res2 += lower[i] * ask(x - 1)add(x, 1)print(res1, res2)
AcWing 242. 一个简单的整数问题
给定长度为 N的数列 A,然后输入 M 行操作指令。
第一类指令形如 C l r d,表示把数列中第 l∼r
个数都加 d
。
第二类指令形如 Q x,表示询问数列中第 x
个数的值。
对于每个询问,输出一个整数表示答案。
输入格式
第一行包含两个整数 N
和 M
。
第二行包含 N
个整数 A[i]
。
接下来 M
行表示 M
条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
1≤N,M≤105
,
|d|≤10000
,
|A[i]|≤109
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4
Q 1
Q 2
C 1 6 3
Q 2
输出样例:
4
1
2
5
思路
C表示对一定区间进行操作,Q表示对单点查询。
转化为差分
对差分数组的单点操作 ≡\equiv≡ 对原数组的区间操作
对差分数组的区间查询 ≡\equiv≡ 对原数组的单点查询
代码
N = 100010a= [0] * N
tr = [0] * Ndef lowbit(x) :return x & -xdef add(x, c) :i = xwhile i <= n :tr[i] += ci += lowbit(i)def ask(x) :res = 0i = xwhile i :res += tr[i]i -= lowbit(i)return resn, m = map(int, input().split())a[1 : n + 1] = list(map(int, input().split()))
# 初始化差分树状数组
for i in range(1, n + 1) :add(i, a[i] - a[i - 1])for i in range(m) :cmd = input()if cmd[0] == "Q" :x = int(cmd.split()[1])print(ask(x))else :l, r, c = map(int, cmd[2 :].split())add(l, c)add(r + 1, -c)
AcWing 244. 谜一样的牛
有 n 头奶牛,已知它们的身高为 1∼n
且各不相同,但不知道每头奶牛的具体身高。
现在这 n
头奶牛站成一列,已知第 i
头牛前面有 Ai
头牛比它低,求每头奶牛的身高。
输入格式
第 1
行:输入整数 n
。
第 2…n
行:每行输入一个整数 Ai
,第 i
行表示第 i
头牛前面有 Ai
头牛比它低。
(注意:因为第 1
头牛前面没有牛,所以并没有将它列出)
输出格式
输出包含 n
行,每行输出一个整数表示牛的身高。
第 i
行输出第 i
头牛的身高。
数据范围
1≤n≤105
输入样例:
5
1
2
1
0
输出样例:
2
4
5
3
1
思路
从后往前,最后一头牛知道自己比前AnA_nAn头牛高,则最后一头牛是An+1A_n+1An+1高的牛。
倒数第二头牛,知道自己比前An−1A_{n-1}An−1头牛高,则当前的牛是除去An+1A_n+1An+1的高度外的An−1+1A_{n-1} + 1An−1+1的高度的牛。
由此可以递推得到所有结果。
这个过程中我们需要维护一个所有未确定高度的数据结构,我们需要对这个数据结构的操作是,查询某个高度是第几高,以及删除某点的高度。
树状数组!!!!
代码
N = 100010tr = [0] * N
a = [0] * Ndef lowbit(x) : return x & -xdef add(x, c) :i = xwhile i <= n :tr[i] += ci += lowbit(i)def ask(x) :res = 0i = xwhile i :res += tr[i]i -= lowbit(i)return resn = int(input())for i in range(2, n + 1) :a[i] = int(input())for i in range(1, n + 1) :add(i, 1)res = [0] * (n + 1)
for i in range(n, 0, -1) :x = a[i] + 1# 找到一个满足第x的高度l, r = 0, nwhile l < r :mid = (l + r) >> 1if ask(mid) >= x :r = midelse :l = mid + 1res[i] = ladd(l, -1)for i in range(1, n + 1) :print(res[i])
总结
树状数组的题,一般需要发掘题目中需要的两种操作,这一点非常关键,剩下实现就肥肠煎蛋。
相关文章:

树状数组讲解
树状数组 文章目录树状数组引入例题AcWing241.楼兰图腾思路代码AcWing 242. 一个简单的整数问题思路代码AcWing 244. 谜一样的牛思路代码总结引入 树状数组主要维护的是这样一个数据结构: tr[x]表示以x为终点的长度为lowbit(x)的前缀和、最大值、最小值、最大公约数…...

每个Android开发都应需知的性能指标~
无论你是发布一个新的 Android 应用,还是希望提高现有应用的性能,你都可以使用 Android 应用性能指标来帮助你。 在这篇文章中,我将解释什么是 Android 应用性能指标,并列出8个需要考虑跟踪的维度和建议的基线。 什么是 Android…...
MSYS2安装
最近在学习windows上编译FFmpeg,需要用到msys2,在此记录一下安装和配置过程。 点击如下链接,下载安装包: Index of /msys2/distrib/x86_64/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 我下载的是:ms…...

3/3考试总结
时间安排 7:30–7:50 看题,怎么感觉三道构造,T3 貌似有网络流背景。 7:50–8:30 T1,有一些简单的性质,缩减两端点后枚举一下翻转的区间就可以了。然后花了一点时间写 spj 调试。 8:30–10:20 T2,比较纯粹的构造题。有网络流做法,…...
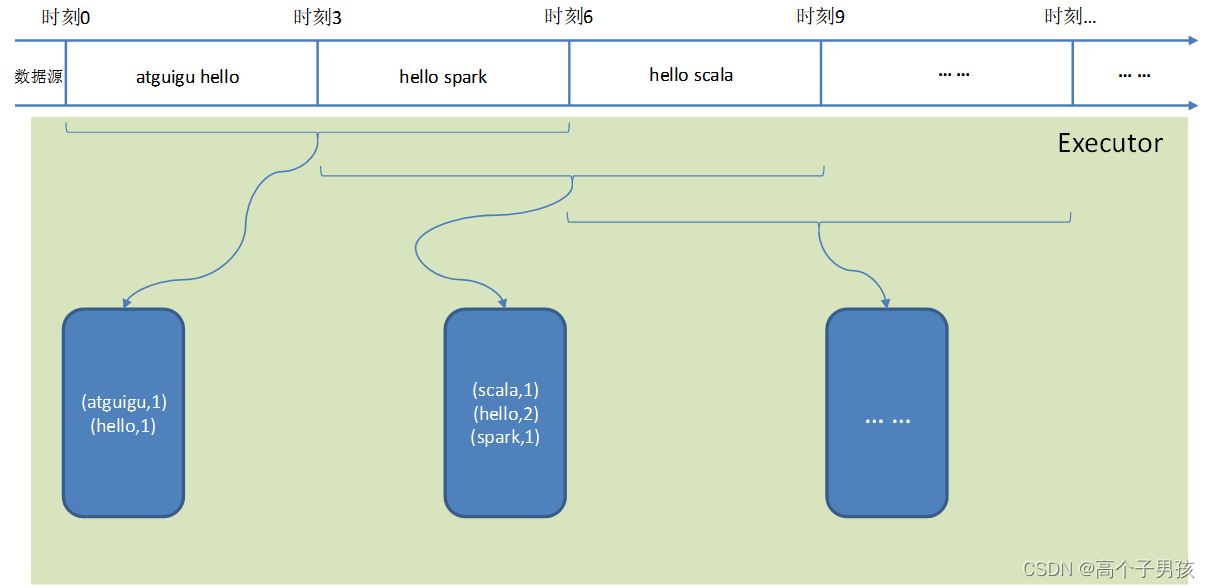
Spark Streaming DStream转换
DStream上的操作与RDD的类似,分为Transformations(转换)和Output Operations(输出)两种,此外转换操作中还有一些比较特殊的算子,如:updateStateByKey()、transform()以及各种Window相…...
水果商城,可运行
文章目录项目介绍一、技术栈二、本项目分为前后台,有管理员与用户两种角色;1、管理员角色包含以下功能:2、用户角色包含以下功能:三、用户功能页面展示四、管理员功能页面展示五、部分代码展示六、获取整套项目源码项目介绍 一、…...
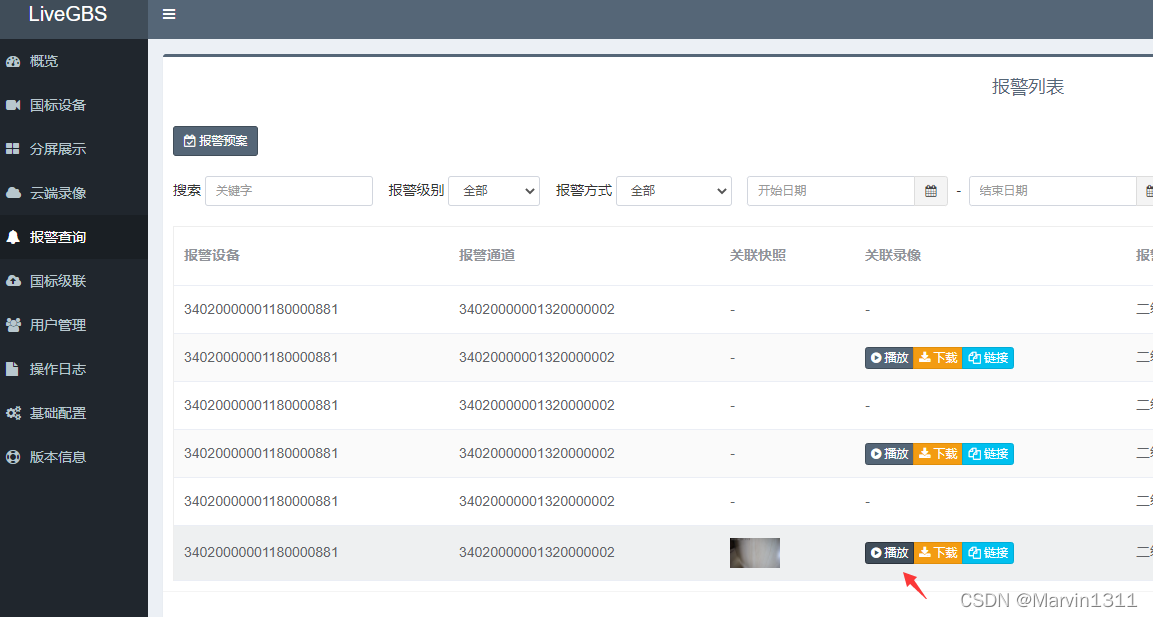
LiveGBS国标GB/T28181国标视频流媒体平台-功能报警订阅配置报警预案告警截图及录像
LiveGBS国标GB/T28181国标视频流媒体平台-功能报警订阅配置报警预案告警截图及录像1、报警信息1.1、报警查询1.2、配置开启报警订阅1.2.1、国标设备编辑1.2.2、选择开启报警订阅1.3、配置摄像头报警1.3.1、配置摄像头报警通道ID1.3.2、配置摄像头开启侦测1.3.3、尝试触发摄像头…...
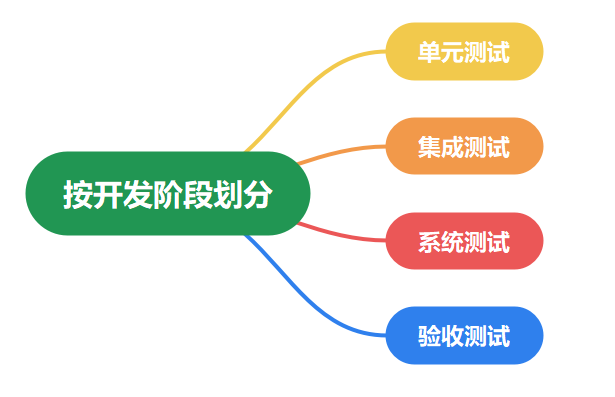
软件测试---测试分类
一 : 按测试对象划分 1.1 可靠性测试 可靠性(Availability)即可用性,是指系统正常运行的能力或者程度,一般用正常向用户提供软件服务的时间占总时间的百分比表示。 1.2 容错性测试 行李箱 , 四个轮子 , 坏了一个 , 说明这个容错…...

剑指 Offer II 015. 字符串中的所有变位词
题目链接 剑指 Offer II 015. 字符串中的所有变位词 mid 题目描述 给定两个字符串 s和 p,找到 s中所有 p的 变位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。 变位词 指字母相同,但排列不同的字符串。 示例 1: 输…...

【SpringCloud】SpringCloud详细教程之微服务比较
目录前言一.什么是微服务?为什么要使用微服务二.微服务对比三.企业开发场景前言 我会通过实际代码来给展示每个组件的用法 一.什么是微服务?为什么要使用微服务 分布式,把一个项目拆分成多个模块,每一个模块相当于一个服务。 微…...
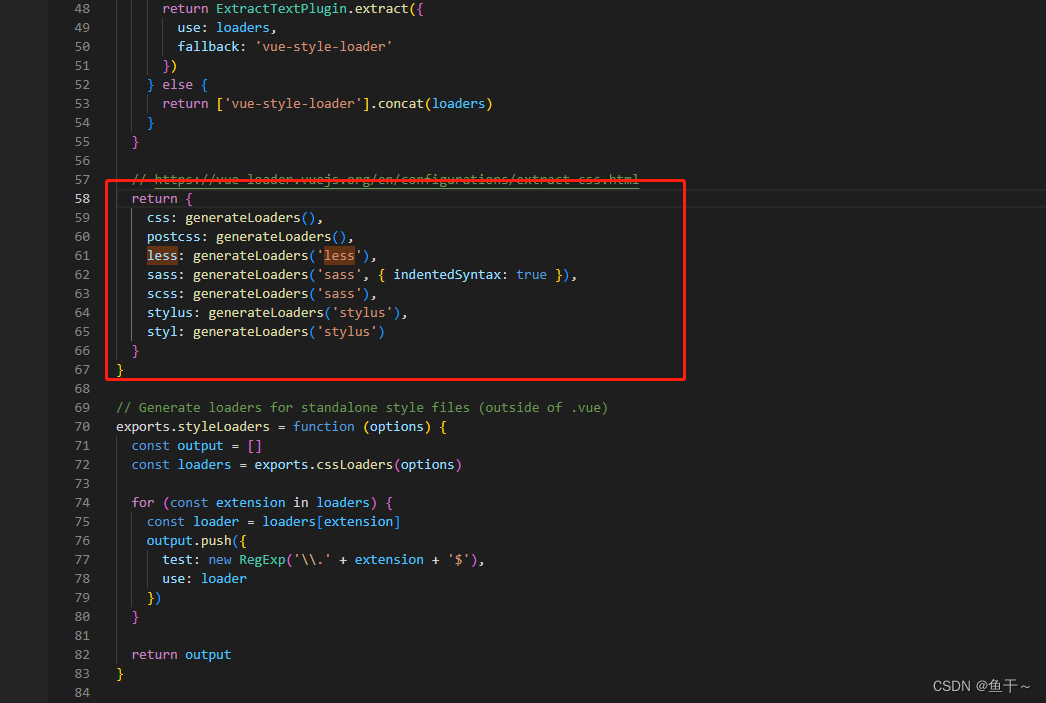
二.项目使用vue-router,引入ant-design-vue的UI框架,引入less
根据前文《使用Vue脚手架工具搭建vue项目》搭建好脚手架后使用 1.vue-router 2.引入UI框架ant design vue 3.引入less 1.vue-router vue-router分为两种模式(默认为hash模式): hash history hash: 特征: 1.hash会在浏览器路径里带#号&#…...

网络安全怎么学?20年白帽子老江湖告诉你
很多人都知道龙叔是个老程序员,但却不知道其实我也是个H客,20年前我就开始痴迷于H客技术,可以说是网络安全方面的老江湖了。 到现在,我还依然会去研究这一块,偶尔会和一些网安的朋友交流技术,比如说红盟的…...
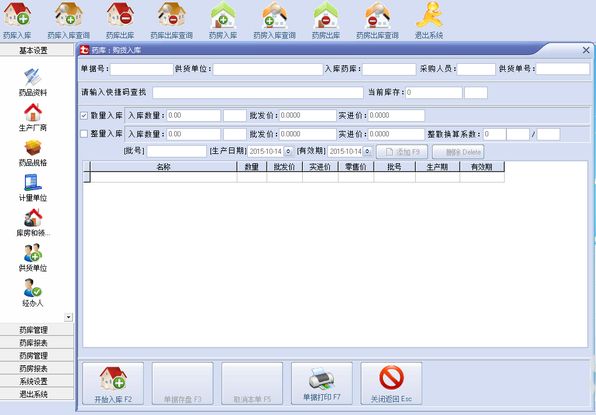
药房管理系统;药库管理系统
第一,主要功能: 本系统集日常销售、药品进销存、会员积分、GSP管理等药店所需的所有功能于一体,实现店铺管理的全部自动化。第二、新功能: 增加了“按功能查询药品”的功能,使软件用户可以根据客户的症状推荐合适…...

深眸科技|机器视觉提升制造性能,焕发传统企业智造新活力!
随着机器视觉技术的成熟与发展,其在工业制造中得到越来越广泛的应用。机器视觉在工业制造领域的应用朝着智能识别、智能检测、智能测量以及智能互联的完整智能体系方向发展。此外,快速变化的市场需求,不断涌入行业的竞争对手,让传…...

ubuntu安装SSH的方法
Ubuntu安装SSH的方法。14版的ubuntu经过测试,默认没有开启SSH,所以需要安装。 1、虚拟机设置网卡为桥接模式,即NAT。12版虚拟机默认的。 2、查看ubuntu使用的ip。 ifconfig即可查看,14版的ubuntu自带这个命令。 3、查看是否pi…...

哪种蓝牙耳机通话效果好?通话清晰的蓝牙耳机推荐
出门的时候,如果戴耳机和别人通话,就不必把耳机摘下来,接电话变得前所未有的简单。现在的蓝牙耳机,已经不是单纯的用来听音乐了,而是一种更好的功能。下面这四款蓝牙耳机不仅适合听歌,通话还清晰࿰…...

IT运维如何完成一场高质量复盘
复盘的终极目标是:还原事实,找到薄弱点加以改进。 提到复盘,很多人的第一反应是线上故障,有人要背锅了。 复盘真正的价值是还原事实,在薄弱处加以改进。如何做一次高质量的复盘,我们给出3点建议。 1、坦…...
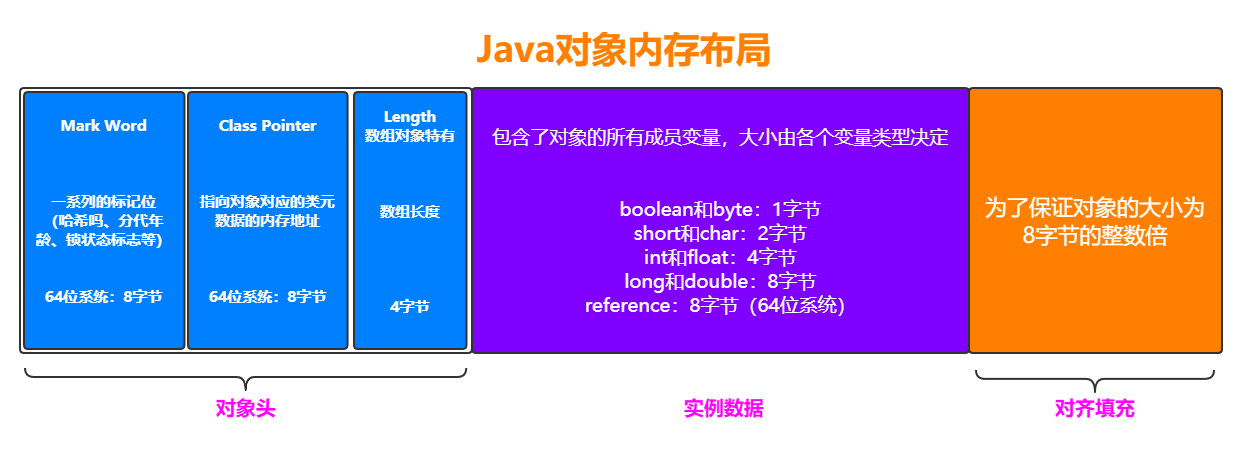
JVM调优面试题——基础知识
文章目录1、JDK,JRE以及JVM的关系2、编译器到底干了什么事?3、类加载机制是什么?3.1、装载(Load)3.2、链接(Link)3.3、初始化(Initialize)4、类加载器有哪些?5、什么是双亲委派机制?6、介绍一下JVM内存划分(…...

三、mongdb 查询
一、 MongoDB文档检索 MongoDB中有多种方式可以检索文档: 1.1 查询过滤器 使用查询过滤器从集合中检索文档。查询过滤器是一组键值对,可按字段值查询文档。 例如: db.col.find({"status":"A"})这个示例查询status等于“A”的文档。 1.2 范围查询操作符…...
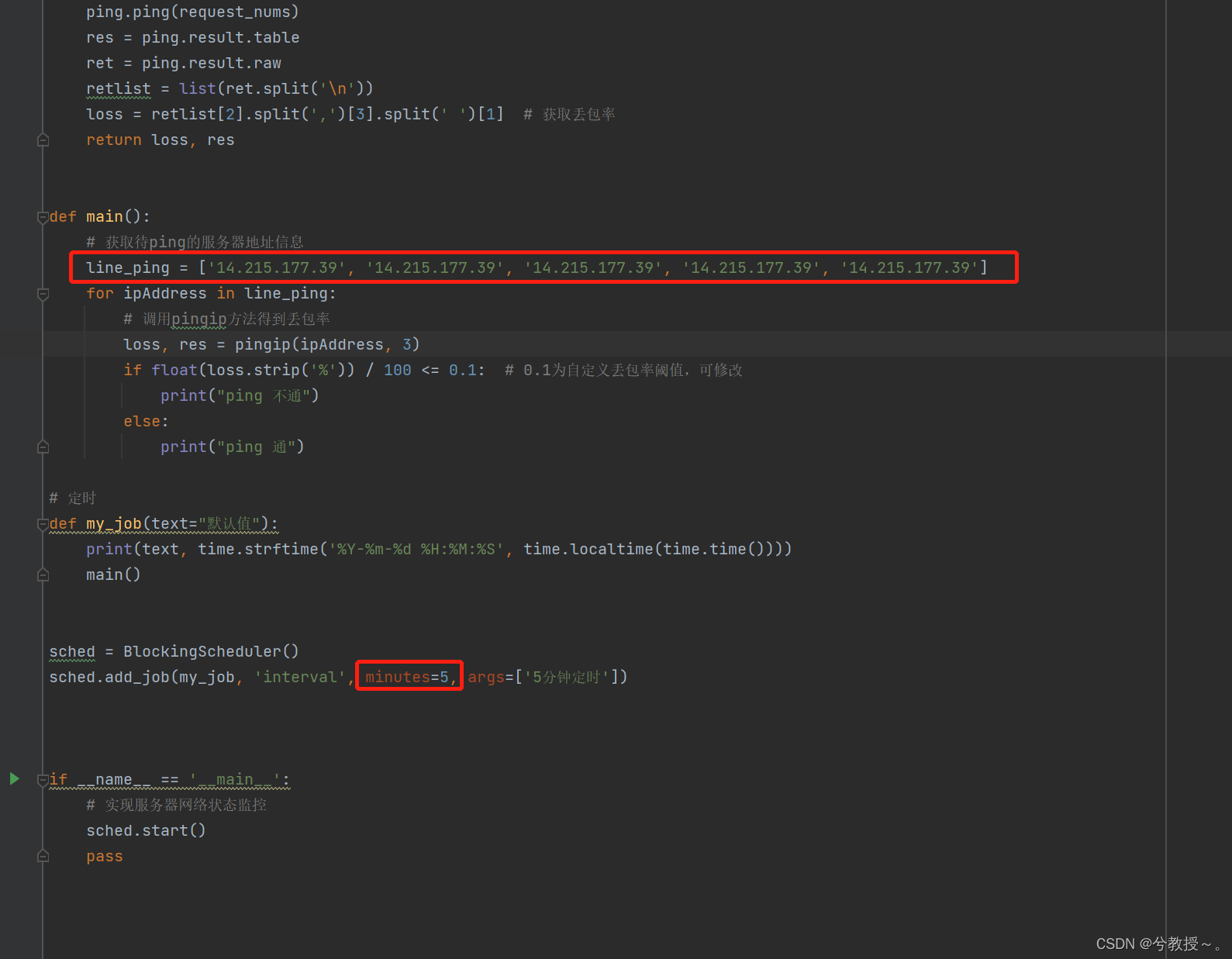
python的 ping 网络状态监测方法(含多IP)
ping 基本概念 ping (Packet Internet Groper)是一种因特网包探索器,用于测试网络连接量的程序。Ping是工作在 TCP/IP网络体系结构中应用层的一个服务命令, 主要是向特定的目的主机发送 ICMP(Internet Control Messag…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...
