【数据结构和算法】寻找数组的中心下标
其他系列文章导航
Java基础合集
数据结构与算法合集设计模式合集
多线程合集
分布式合集
ES合集
文章目录
其他系列文章导航
文章目录
前言
一、题目描述
二、题解
2.1 前缀和的解题模板
2.1.1 最长递增子序列长度
2.1.2 寻找数组中第 k 大的元素
2.1.3 最长公共子序列长度
2.1.4 寻找数组中第 k 小的元素
2.2 方法一:前缀和
三、代码
3.2 方法一:前缀和
四、复杂度分析
4.2 方法一:前缀和
前言
这是力扣的 724 题,难度为简单,解题方案有很多种,本文讲解我认为最奇妙的一种。
这是一道非常经典的前缀和问题,虽然看似简单,但它却能让你深入理解前缀和的特点。
一、题目描述
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
示例 1:
输入:nums = [1, 7, 3, 6, 5, 6] 输出:3 解释: 中心下标是 3 。 左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 , 右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
示例 2:
输入:nums = [1, 2, 3] 输出:-1 解释: 数组中不存在满足此条件的中心下标。
示例 3:
输入:nums = [2, 1, -1] 输出:0 解释: 中心下标是 0 。 左侧数之和 sum = 0 ,(下标 0 左侧不存在元素), 右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。
提示:
1 <= nums.length <= 104-1000 <= nums[i] <= 1000
二、题解
2.1 前缀和的解题模板
前缀和算法是一种在处理数组或链表问题时常用的技巧,它可以有效地减少重复计算,提高算法的效率。下面是一些常见的使用前缀和算法的题目以及解题思路:
2.1.1 最长递增子序列长度
题目描述:给定一个无序数组,求最长递增子序列的长度。
解题思路:可以使用前缀和和单调栈来解决这个问题。首先,遍历数组,计算出前缀和。然后,使用单调栈记录当前递增子序列的起始位置。遍历数组时,如果当前元素大于前缀和,说明可以扩展当前递增子序列,将当前位置入栈。如果当前元素小于等于前缀和,说明当前递增子序列已经结束,弹出栈顶元素。最后,栈中剩余的元素即为最长递增子序列的起始位置,计算长度即可。
2.1.2 寻找数组中第 k 大的元素
题目描述:给定一个无序数组和一个整数k,找到数组中第k大的元素。
解题思路:可以使用前缀和和快速选择算法来解决这个问题。首先,计算出数组的前缀和。然后,使用快速选择算法在数组中找到第k小的元素。具体实现中,每次选择一个枢轴元素,将数组分成两部分,小于枢轴的元素和大于枢轴的元素。如果枢轴左边的元素个数小于k,则在左边的子数组中继续查找;如果枢轴左边的元素个数大于等于k,则在右边的子数组中继续查找。最后,当找到第k小的元素时,返回该元素即可。
2.1.3 最长公共子序列长度
题目描述:给定两个字符串,求最长公共子序列的长度。
解题思路:可以使用动态规划算法来解决这个问题。如果字符串长度分别为m和n,则可以定义一个二维数组dp[m+1][n+1],其中dp[i][j]表示字符串s1的前i个字符和字符串s2的前j个字符的最长公共子序列长度。根据动态规划的思想,状态转移方程为dp[i][j] = max(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])。如果s1[i-1]等于s2[j-1],则dp[i][j] = dp[i-1][j-1] + 1;否则dp[i][j]取其他两种情况中的较大值。最终结果为dp[m][n]。
2.1.4 寻找数组中第 k 小的元素
题目描述:给定一个无序数组和一个整数k,找到数组中第k小的元素。
解题思路:可以使用前缀和和快速选择算法来解决这个问题。具体实现与寻找第k大元素类似,只不过最后返回的是第k小的元素而非第k大的元素。
2.2 方法一:前缀和
题目仅说明是整数数组,无其他已知条件,因此考虑直接遍历数组。

- 设索引 i 对应变量「左侧元素相加和 leftSum」和「右侧元素相加和 rightSum」。
- 遍历数组 nums ,每轮更新 leftSum 和 rightSum。
- 遍历中,遇到满足 leftSum == rightSum 时,说明当前索引为中心下标,返回即可。
- 若遍历完成,仍未找到「中心下标」,则返回 -1 。
初始化时,相当于索引 i=−1 ,此时 leftSum = 0 , rightSum = 所有元素的和 。
需要考虑大数越界问题。题目给定整数数组 nums ,并给定取值范围。
题目的范围在 int 类型的取值范围内,因此 sum_left 和 sum_right 使用 int 类型即可。
三、代码
3.2 方法一:前缀和
Java版本:
class Solution {public int pivotIndex(int[] nums) {int leftSum = 0, rightSum = Arrays.stream(nums).sum();for (int i = 0; i < nums.length; i++) {rightSum -= nums[i];if (leftSum == rightSum) return i;leftSum += nums[i];}return -1;}
}C++版本:
class Solution {
public:int pivotIndex(vector<int>& nums) {int leftSum = 0, rightSum = accumulate(nums.begin(), nums.end(), 0);for (int i = 0; i < nums.size(); i++) {rightSum -= nums[i];if (leftSum == rightSum) return i;leftSum += nums[i];}return -1;}
};
Python版本:
class Solution:def pivotIndex(self, nums: List[int]) -> int:left_sum, right_sum = 0, sum(nums)for i in range(len(nums)):right_sum -= nums[i]if left_sum == right_sum:return ileft_sum += nums[i]return -1
Go版本:
package mainfunc pivotIndex(nums []int) int {leftSum := 0rightSum := 0for _, v := range nums {rightSum += v}for i, v := range nums {rightSum -= vif leftSum == rightSum {return i}leftSum += v}return -1
}
四、复杂度分析
4.2 方法一:前缀和
时间复杂度 O(N): 其中 N 为数组 nums 长度。求和操作使用 O(N) 线性时间,遍历 nums 最差使用 O(N) 线性时间。
空间复杂度 O(1): 变量 leftSum , rightSum 使用常数大小空间。
相关文章:

【数据结构和算法】寻找数组的中心下标
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、题目描述 二、题解 2.1 前缀和的解题模板 2.1.1 最长递增子序列长度 2.1.2 寻找数组中第 k 大的元素 2.1.3 最长公共子序列…...
多粒度在研究中的应用
FontDiffuser: One-Shot Font Generation via Denoising Diffusion with Multi-Scale Content Aggregation and Style Contrastive Learning 存在的问题 现有的字体生成方法虽然取得了令人满意的性能,但在处理复杂字和风格变化较大的字符(尤其是中文字符)时&#x…...

Docker命令---查看容器日志
介绍 使用docker命令查看容器输出的日志 示例 docker logs 容器ID...
Spring Boot 基于Redisson实现注解式分布式锁
依赖版本 JDK 17 Spring Boot 3.2.0 Redisson 3.25.0 源码地址:Gitee 导入依赖 <properties><redisson.version>3.25.0</redisson.version> </properties><dependencies><dependency><groupId>org.projectlombok</…...

Javascript 正则表达式零宽断言
在介绍正则表达式零宽断言这个概念之前,先看一下以下这道有关 javascript 正则表达式的题目: 登录注册流程是前端最常见的业务流程之一,注册流程少不了密码强弱度校验,请实现对密码的校验,要求满足: 包含大…...

Chocolatey
Chocolatey Software | PHP (Hypertext Preprocessor) 8.3.1 msi安装包https://github.com/chocolatey/choco/releases/download/2.2.2/chocolatey-2.2.2.0.msi 设置/安装 巧克力味Chocolatey CLI (choco)设置/安装 要求 受支持的 Windows 版本Windows …...

雍禾植发成毛发行业标杆!雍禾医疗获“年度医疗大健康消费企业”
近期,以“新视野 新链接”为主题的2023 EDGE AWARDS全球创新评选榜单正式发布。该评选由钛媒体发起,聚焦大健康产业,由权威行业专家、王牌分析师、专业投资机构、用户代表共同评审,兼顾综合专业性、影响力、创新性三大维度评选而出…...
共享内存和信号量)
Linux内核--进程管理(十二)共享内存和信号量
目录 一、引言 二、基础知识 三、统一封装的接口 ------>3.1、kern_ipc_perm 四、共享内存的创建和映射 ------>4.1、创建共享内存 ------>4.2、共享内存的映射 五、信号量的创建和使用 ------>5.1、信号量的创建 ------>5.2、信号量的初始化 ------…...

java 构造方法
构造方法 1、什么是构造方法,有什么用? 构造方法是一个比较特殊的方法,通过构造方法可以完成对象的创建,以及实例变量的初始化。 换句话说:构造方法是用来创建对象,并且同时给对象的属性赋值。 注意&#x…...

CISSP 第2章: 人员安全和风险管理概念
第二章 人员安全和风险管理概念 2.1 促进人员安全策略 构建工作描述方面的重要因素包括: 职责分离: 把关键的、重要的和敏感工作任务分配给若干不同的管理员或高级执行者,防止共谋 工作职责:最小特权原则 岗位轮换:提供知识冗余,减少伪造、数据更改、偷…...
一)
前端八股文(CSS篇)一
目录 1.px和em的区别 2.介绍下BFC及其应用 3.介绍下粘性布局(sticky) 4.清除浮动的方法 5.如何用css或js实现多行文本溢出省略效果,考虑兼容 6.如何触发重排和重绘? 7.重绘与重排的区别? 8.说说两种盒模型以及区…...

游戏加速器LSP/DLL导致WSL.EXE无法打开问题修复!
解决办法: https://github.com/microsoft/WSL/issues/4177#issuecomment-597736482 方法一:(管理员身份) netsh winsock reset 方法二: WSCSetApplicationCategory 函数设置LSP加载权限 bool NoLsp(const wchar_t* …...

宏电股份5G RedCap终端产品助力深圳极速先锋城市建设
12月26日,“全城全网,先锋物联”深圳移动5G-A RedCap助力深圳极速先锋城市创新发布会举行,宏电股份携一系列5G RedCap终端产品应邀参与创新发布会,来自全国5G生态圈的各界嘉宾、专家学者济济一堂,共探信息化数字化创新…...

linux top命令中 cpu 利用率/mem 使用率与load average平均负载计算方式
文章目录 1 简介2 CPU% 字段3 MEM% 字段4 load average 平均负载 1 简介 top 命令是 Linux 上一个常用的系统监控工具,它经常用来监控 Linux 的系统状态,是常用的性能分析工具,能够显示较全的系统资源信息,包括系统负载ÿ…...
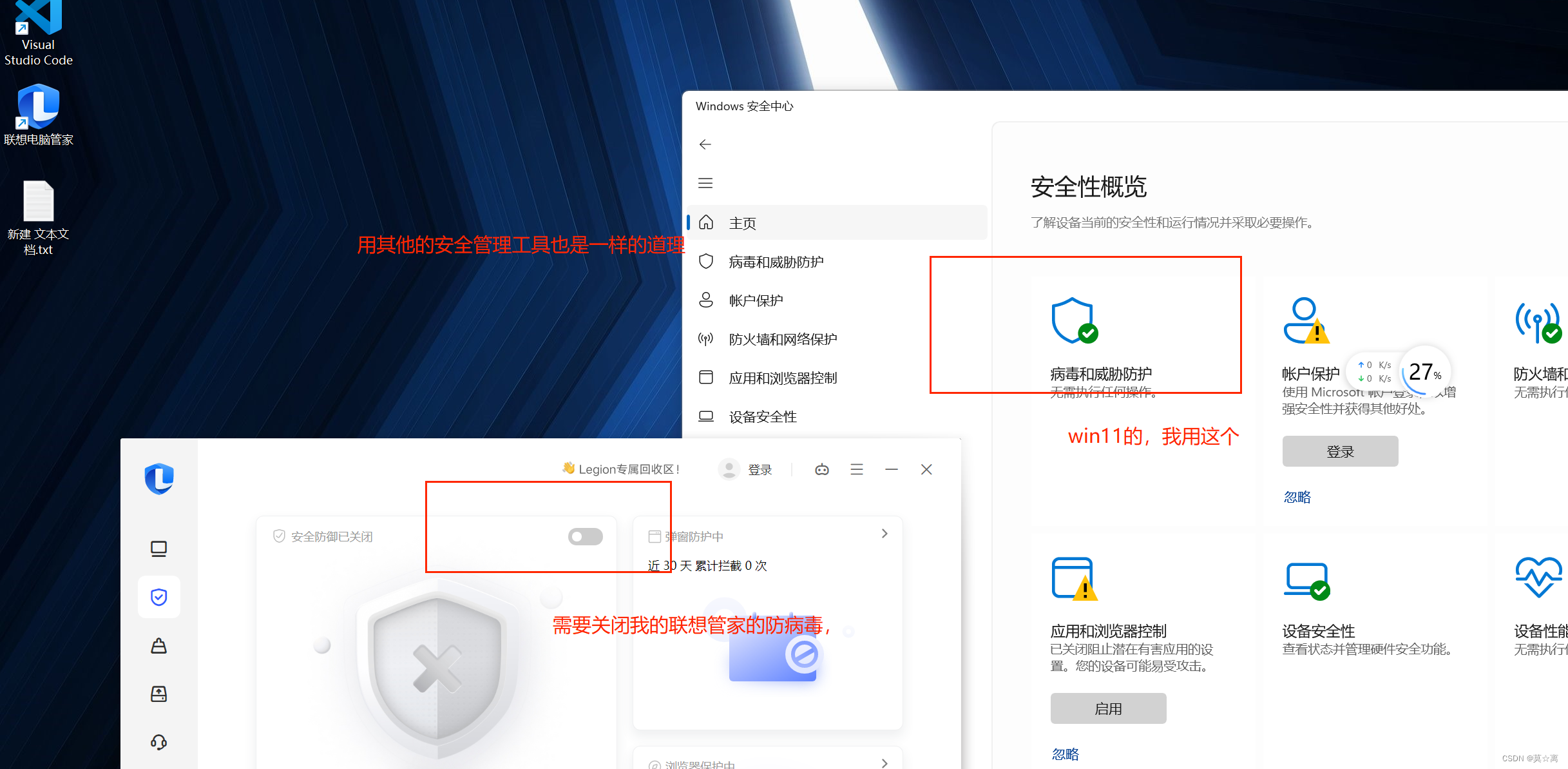
win11出现安全中心空白和IT管理员已限制对某些区域的访问(不一样的解决方式),真实的个人经历,并且解决经过
1、个人的产生问题的经历 2023年12月22日,由于我买了一块电脑的固态硬盘1T,想要扩容,原来电脑自带512G(由于个人是一个程序员,导致512G实在太古鸡肋)装好以后,想要重装一下系统,来个大清理。结果不出意料&…...

关于安卓重启设备和重启应用进程
android 重启应用进程 //多种方式重启应用进程public class MainActivity {//重启当前Applicationprivate void restartApplication(){final Intent intent getPackageManager().getLaunchIntentForPackage(getPackageName());intent.addFlags(Intent.FLAG_ACTIVITY_CLEAR_TOP…...
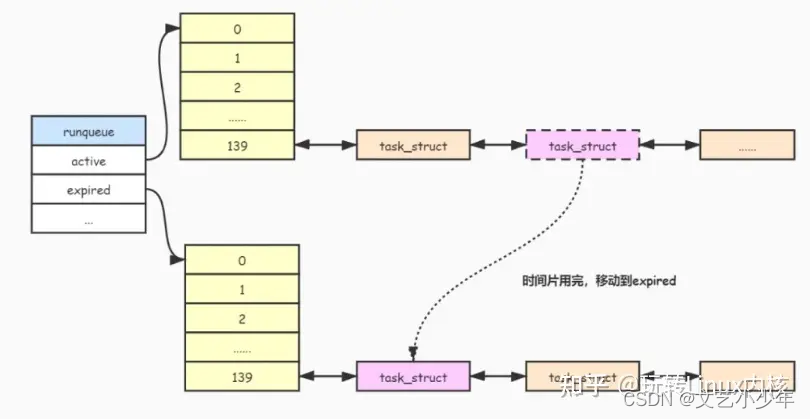
Linux内核--进程管理(十三)O(1)调度算法
目录 一、引言 二、O(1)调度算法原理 ------>2.1、prio_array 结构 ------>2.2、runqueue 结构 三、实时进程调度 四、普通进程调度 ------>4.1、运行时间片计算 五、O(1)调度算法实现 ------>5.1、时钟中断任务调度 ------>5.2、任务调度 一、引言 …...

【QT】发生的运行时错误汇总
1 、QObject::startTimer: Timers cannot be started from another thread 错误原因:QObject是可重入的,它的大多数非GUI子类,例如QTimer, QTcpSocket, QUdpSocket and QProcess都是可重入的,使得这些类可以同时用于多线程。需要…...
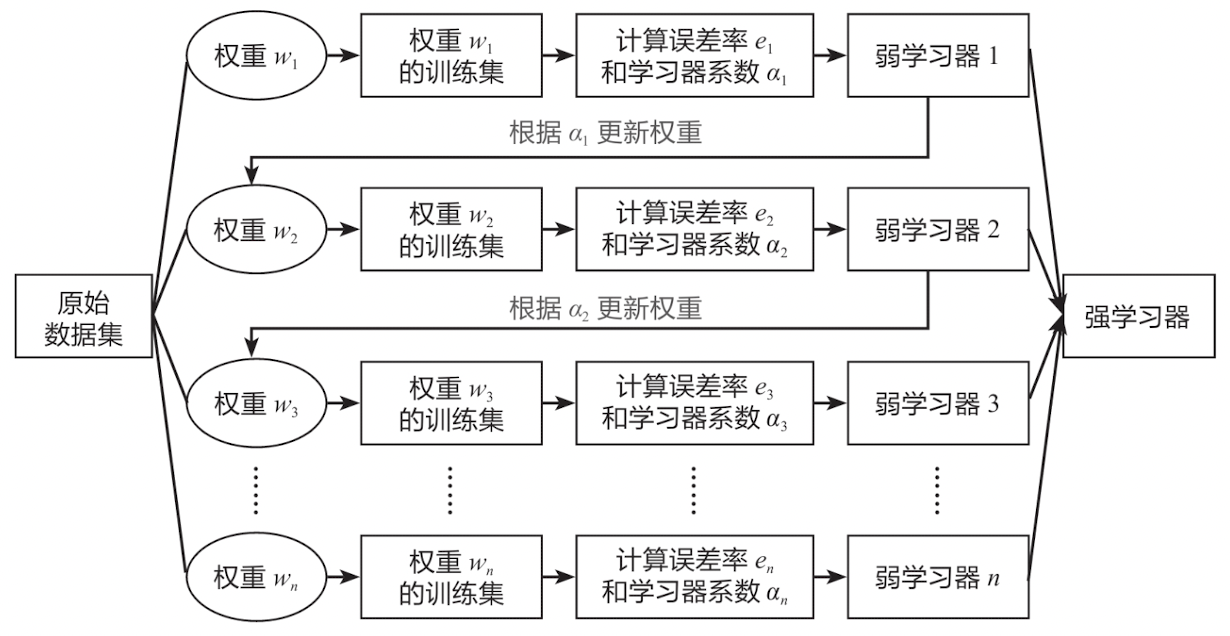
机器学习常用算法模型总结
文章目录 1.基础篇:了解机器学习1.1 什么是机器学习1.2 机器学习的场景1.2.1 模式识别1.2.2 数据挖掘1.2.3 统计学习1.2.4 自然语言处理1.2.5 计算机视觉1.2.6 语音识别 1.3 机器学习与深度学习1.4 机器学习和人工智能1.5 机器学习的数学基础特征值和特征向量的定义…...

笔记中所得(已删减)
1.交流电的一个周期内电压/电流的平均值都为0 2.电动势:电池将单位正电荷由负极搬到正极所做的功 5.额定能量:电池的额定容量乘以标称电压,以Wh为单位 6.500mAh意义是可以以500mA的电流放电1小时 7.电池容量的单位是mAh 13.实际电流源不能串联 14. 15. 16. 17. 18. 19.电…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
