【MPC学习笔记】01:MPC简介(Lecture 1_1 Unconstrained MPC)
本笔记来自北航诸兵老师的课程
课程地址:模型预测控制(2022春)lecture 1-1 Unconstrained MPC
文章目录
- 0 MPC 简介
- 0.1 案例引入
- 0.2 系统模型
- 0.3 MPC的优点
- 0.4 MPC的缺点
- 0.5 MPC的未来
- 1 详细介绍
0 MPC 简介
0.1 案例引入
MPC(Model Predictive Control)模型预测控制,是预测控制的一种,是基于模型来进行控制的。
老师举了下面这个例子来引入MPC的基本思想:
比方说我们为未来的一段时间制定计划,一天中几点到几点该做什么。但是计划赶不上变化,出现变化,出现拖延,计划就得做相应的调整。过了一段时间,根据计划的实际落实情况,再对接下来的计划进行调整。如此往复。不断地执行计划,也不断地修订计划。
0.2 系统模型
在控制系统中,有惯用表示:输入记作 u u u,状态变量记作 x x x,输出记作 y y y
假设系统是离散的,系统的状态方程为:
x ( k + 1 ) = f ( x ( k ) , u ( k ) ) x(k+1)=f(x(k),u(k)) x(k+1)=f(x(k),u(k))
实际上系统可以是,线性的或非线性的,连续的或离散的或既包含连续又包含离散的,确定的或随机的,只要满足该方程即可
设当前时刻为 k k k,当前状态为 x ( k ) x(k) x(k)
在输入 u ( k ) u(k) u(k) 的作用下,系统的状态将由 x ( k ) x(k) x(k) 变为 x ( k + 1 ) x(k+1) x(k+1)
在输入 u ( k + 1 ) u(k+1) u(k+1) 的作用下,系统的状态将由 x ( k + 1 ) x(k+1) x(k+1) 变为 x ( k + 2 ) x(k+2) x(k+2)
在输入 u ( k + 2 ) u(k+2) u(k+2) 的作用下,系统的状态将由 x ( k + 2 ) x(k+2) x(k+2) 变为 x ( k + 3 ) x(k+3) x(k+3)
…
由上面的列举,知:输入序列➡️输出序列
但在此时,也就是时刻 k k k ,我们并不知道输入序列 { u ( k ) , u ( k + 1 ) , u ( k + 2 ) , ⋯ } \{u(k),u(k+1),u(k+2),\cdots\} {u(k),u(k+1),u(k+2),⋯} 是多少
自然而然就会想到一个问题——怎么确定输入序列?
答:通过优化的方式,Optimization
将 状态序列 记为 X ( k ) X(k) X(k)
将 输入序列 记为 U ( k ) U(k) U(k)
输入序列的求解,可用如下优化问题的公式来描述:
U ∗ ( k ) = a r g m i n ∑ i = k ∞ l ( x ( i ) , u ( i ) ) = { u ∗ ( k ) , u ∗ ( k + 1 ) , … } s . t . x ∈ X , u ∈ U \begin{aligned} U^*(k) &= arg\ min\sum^{\infin}_{i=k}l(x(i),u(i)) \\ &=\{u^*(k),u^*(k+1),\dots\} \\ \\ s.t.\quad &x\in \mathscr{X}, u\in \mathscr {U} \end{aligned} U∗(k)s.t.=arg mini=k∑∞l(x(i),u(i))={u∗(k),u∗(k+1),…}x∈X,u∈U
其中, a r g m i n arg\ min arg min 表示使 **代价函数(目标函数)**取值最小时,输入序列 U ( k ) U(k) U(k) 的取值; ∗ ^* ∗ 表示最优解; s . t . s.t. s.t. 表示约束条件; l ( x ( i ) , u ( i ) ) l(x(i),u(i)) l(x(i),u(i)) 称为 “Stage cost”。
令 u ( k ) = u ∗ ( k ) u(k)=u^*(k) u(k)=u∗(k) ,舍弃求出的 U ∗ ( k ) U^*(k) U∗(k) 中后续其他时刻的输入,则由 x ( k + 1 ) = f ( x ( k ) , u ( k ) ) x(k+1) = f(x(k),u(k)) x(k+1)=f(x(k),u(k)) 可以求出时刻 k + 1 k+1 k+1 的状态
接着, k + 1 k+1 k+1 变为当前时刻,重复上述步骤,求出时刻 k + 2 k+2 k+2 的状态 x ( k + 2 ) x(k+2) x(k+2),…
以上就是MPC的基本原理
如果只优化一次,将计算出的 U ( k ) U(k) U(k) 序列依次执行,那么就变成了开环优化;而这里每一时刻优化后都只取 u ∗ ( k ) u^*(k) u∗(k) 执行( u ∗ ( k ) u^*(k) u∗(k)是 x ( k ) x(k) x(k)的函数),并且不断进行优化,构成滚动优化(闭环优化), 因此MPC实际上引入了反馈
0.3 MPC的优点
- 处理控制输入和系统状态上的约束(Constraints)
- 约束来源:actuator limits; safety; environmental; economic constraints
- PID没办法解决约束问题
- 近似最优控制
- 与线性系统中的最优控制(LQR, 线性二次型调节器)有区别,在LQR中,我们找到的是最优的增益 k k k(假设,已知系统是线性反馈),MPC找的是 u u u
0.4 MPC的缺点
- 需要在线优化(online optimization),可能会有较大的计算负载
0.5 MPC的未来
随着计算机算力提升,MPC或替代PID成为工业界控制主流

1 详细介绍
见【MPC学习笔记】02:MPC详细简介(Lecture 1_1 Unconstrained MPC)
相关文章:

【MPC学习笔记】01:MPC简介(Lecture 1_1 Unconstrained MPC)
本笔记来自北航诸兵老师的课程 课程地址:模型预测控制(2022春)lecture 1-1 Unconstrained MPC 文章目录 0 MPC 简介0.1 案例引入0.2 系统模型0.3 MPC的优点0.4 MPC的缺点0.5 MPC的未来 1 详细介绍 0 MPC 简介 0.1 案例引入 MPC(…...
c语言结构体学习上篇
文章目录 前言一、结构体的声明1,什么叫结构体?2,结构体的类型3,结构体变量的创建和初始化4,结构体的类型5,结构体的初始化 二、结构体的访问1,结构体成员的点操作符访问2,结构体体成员的指针访问 前言 昨…...

Linux: eBPF: bcc-tools:tcpdrop使用需要注意的问题
最近使用bcc-tools的时候注意到,bcc-tools(eBPF相关软件)的使用版本和内核的版本紧密程度非常高。因为要使用内核的函数或者结构体,所以就必须版本一致是必须的,不然会出现下面的警告或者错误: WARNING: tcp_drop() kernel function not found or traceable. The kernel …...

AI:113-基于卷积神经网络的图像风格迁移
🚀点击这里跳转到本专栏,可查阅专栏顶置最新的指南宝典~ 🎉🎊🎉 你的技术旅程将在这里启航! 从基础到实践,深入学习。无论你是初学者还是经验丰富的老手,对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带有在本地跑过的关键代码,详细讲解供…...

15、Kubernetes核心技术 - 探针
目录 一、概述 二、探针类型 2.1、就绪探针(Readiness Probe) 2.2、存活探针(Liveness Probe) 三、探针探测方法 3.1、exec 3.2、httpGet 3.3、tcpSocket 四、探针配置项 五、探针使用 5.1、就绪探针(Readin…...

GTK4 环境配置
1 安装gtk4包裹: # sudo yum install gtk4 gtk4-devel gtk4-devel-docs devhelp glib2 glib2-devel glib2-doc 2 安装 glade 4 git clone https://github.com/ag-python/cambalache.git 记住 把软件目录 复制到 一个你不会移动删除的地方(千万别删除这个软件文件夹 因为运行…...

Yolov8部署——segmentation部署以及批量推理
Yolov8部署——segmentation部署以及批量推理 参考:在windows上部署Yolov8主要参考下面两个仓库,https://github.com/xunzixunzi/tensorrt-cpp-api和https://github.com/xunzixunzi/YOLOv8-TensorRT-CPP,代码说是适合批量处理,但是代码中是以…...

再见2023,你好2024!
大家好,我是老三,本来今天晚上打算出去转一转,陆家嘴打车实在太艰难了,一公里多的路,司机走了四十分钟,还没到,再加上身体不适,咳嗽地比较厉害,所以还是宅在酒店里&#…...
【计算机毕业设计】SSM二手交易网站
项目介绍 该项目分为前后台,前台普通用户角色,后台管理员角色。 管理员主要功能如下: 登陆,商品分类管理,商品管理,商品订单管理,用户管理等功能。 用户角色主要功能如下: 包含以下功能:查看所有商品,用户登陆注册…...

纠删码ReedSolomon
随着大数据技术的发展,HDFS作为Hadoop的核心模块之一得到了广泛的应用。为了数据的可靠性,HDFS通过多副本机制来保证。在HDFS中的每一份数据都有两个副本,1TB的原始数据需要占用3TB的磁盘空间,存储利用率只有1/3。而且系统中大部分…...
)
C++音视频开发技巧汇总(持续更新)
1.录制PCM数据 有时候我们需要录制PCM数据到文件以测试录制数据是否正确,一般可以使用以下代码实现: FILE *pf; fopen_s(&pf, "rec.pcm", "wb"); fwrite(myPcmArr, 1, outBufferLen, pf); 录制pcm文件后可以使用Audacity来导…...
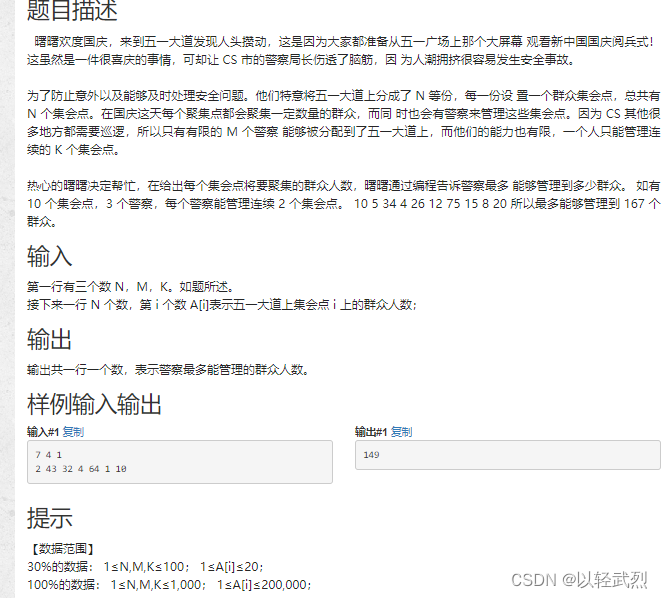
4462 4.曙曙献爱心
#include<bits/stdc.h> using namespace std; int n,m,k; int a[1001]; int s[1001]; int f[1001][1001];//f[i][j],i个警察,j个点,能管理的最大人数 int main(){cin>>n>>m>>k;for(int i1;i<n;i){cin>>a[i…...

浅谈命令模式
命令模式是一种行为设计模式,用于将一个请求封装成一个对象,从而使得请求的发送者和接收者解耦,并支持对请求进行参数化、队列化、撤销和重做等操作。 在命令模式中,有一下介个关键角色: Command(命令&am…...

软件测试/测试开发丨Python 模块与包
python 模块与包 python 模块 项目目录结构 组成 package包module模块function方法 模块定义 定义 包含python定义和语句的文件.py文件作为脚本运行 导入模块 import 模块名from <模块名> import <方法 | 变量 | 类>from <模块名> import * 注意&a…...
java企业网站系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 java Web企业网站系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0&…...
MAC电脑安装java开发工具
一、安装brew 1.1、官网地址 链接 1.2、更新地址 二、安装 java brew install openjdk11 三、安装gradle Gradle安装与配置教程 - 知乎 四、GIT 4.1、GIT安装 brew install git 4.2、rsa ssh-keygen -t rsa -C "jhestarbucks.com" 五、自动搭建一个springBoot…...
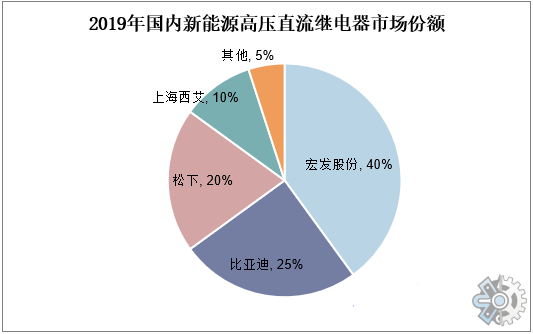
高压继电器,未来几年市场将保持稳定增长
高压继电器是一种用于控制大功率电气设备的开关装置,广泛应用于电力系统、轨道交通、工业自动化等领域。随着各行业对电气控制需求的不断增加,高压继电器市场也在不断扩大。全球高压继电器市场分析: 在全球市场中,目前主要的高压继…...

在Go语言中实现HTTP请求的缓存
大家好,我是你们可爱的编程小助手,今天我们要一起探讨如何使用Go语言实现HTTP请求的缓存。听起来是不是很酷?让我们开始吧! 首先,我们要明白什么是缓存。简单来说,缓存就是将数据存储在内存中,…...

技术扫盲:如何优雅的使用 java -jar
java -jar xxx.jar java -jar 是一个用于在命令行界面中执行 Java 可执行 JAR 文件的命令。它的语法如下: java -jar <JAR 文件路径> [参数]其中: java 是 Java 运行时环境的可执行文件。-jar 是一个选项,表示要执行的文件是一个 JA…...
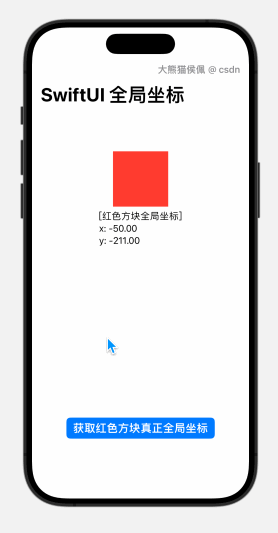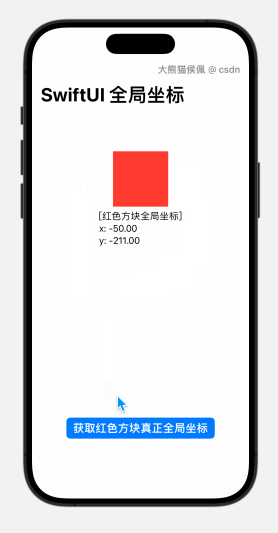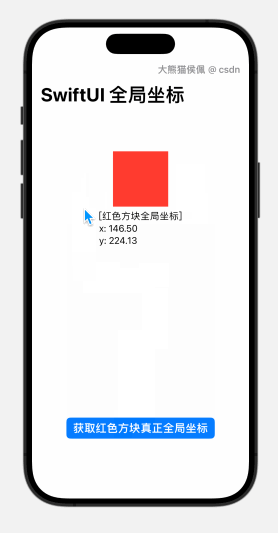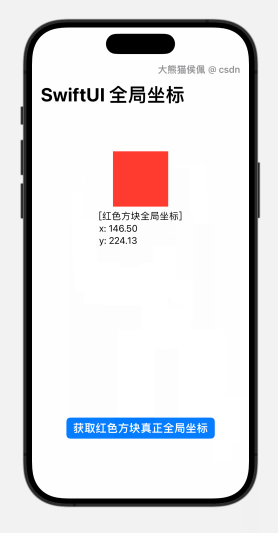
『番外篇七』SwiftUI 获取视图全局位置在 NavigationStack 中失效的解决方法
概览 在 番外篇六』SwiftUI 取得任意视图全局位置的三种方法 这篇博文里,我们详细讨论了在 SwiftUI 中获取任意视图全局坐标的几种方法。 不过,我们也从中提到了某些方法无法适用于 NavigationStack 视图,本篇博文由此应运而生。 在本篇博文种,您将学到如下内容: 概览1.…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
