前缀和算法 -- 寻找数组的中心坐标

 个人主页：Lei宝啊 

愿所有美好如期而遇

---

本题链接

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

输入描述

给定一个数组，接口为int pivotIndex(vector<int>& nums)

输出描述

我们以示例1为例画图解释：

我们返回下标3。

算法分析

算法一：暴力求解

直接遍历数组，外层遍历到哪个i，里层就遍历一次整个数组求和比较，时间复杂度为O(N^2)，这种时间复杂度我们不能接受。

算法二：前缀和

方法一：

我们创建dp表，dp[i]表示从下标0到下标i的元素和，用一个变量sum记录。

预处理dp表

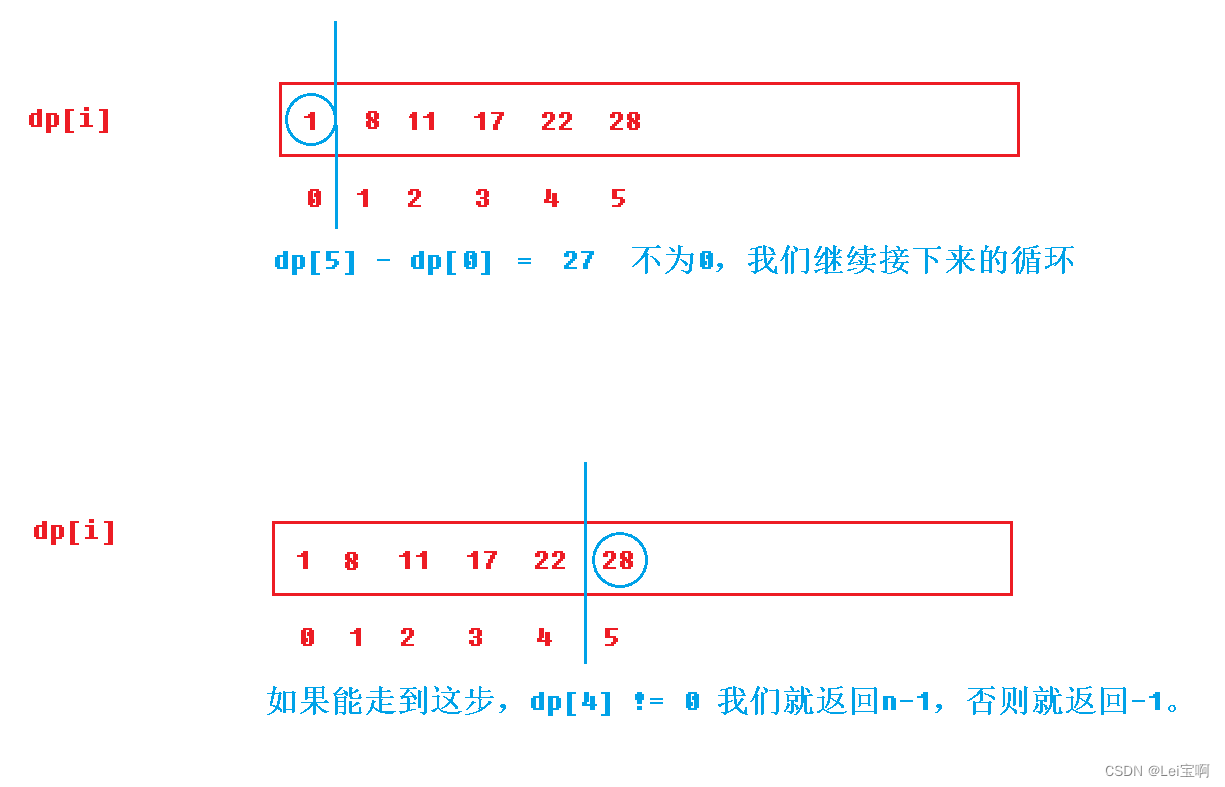
使用dp表计算

接下来我们仍然是遍历数组，但是我们需要提前计算出边界问题，一个是0位置的边界，一个是n-1位置的边界(这个边界在循环后判断)，我们根据上图来判断一下0这个边界，0的左边什么都没有，题目使其和为0，所以我们判断dp[n-1] - dp[0] == 0就return 0，否则继续我们的循环，我们的循环从1开始，到n-1边界结束，然后判断这个边界，即dp[n-2] == 0，我们return n-1; 否则就是没有找到这样的中间下标，我们返回-1。

 

解题源码：

class Solution 
{
public:int pivotIndex(vector<int>& nums){int n = nums.size();int sum = 0;vector<int> dp(n, 0);//dp[i]表示i位置及其前部分的和for (int i = 0; i < n; i++){sum += nums[i];dp[i] = sum;}if (dp[n - 1] - dp[0] == 0) return 0;for (int i = 1; i < n - 1; i++){if (dp[i - 1] == dp[n - 1] - dp[i]){return i;}}if (dp[n - 2] == 0) return n - 1;return -1;}
};

方法二：

我们创建前缀和dp表和后缀和dp表，这里的dp[i]和我们方法一的含义是不同的，这里的dp[i]意为下标0到下标i-1的和，那么dp[i-1]意为下标0到下标i-2的和，以此类推。

预处理dp表

前缀和是从前往后加，后缀和是从后往前加，什么意思呢？我们看图

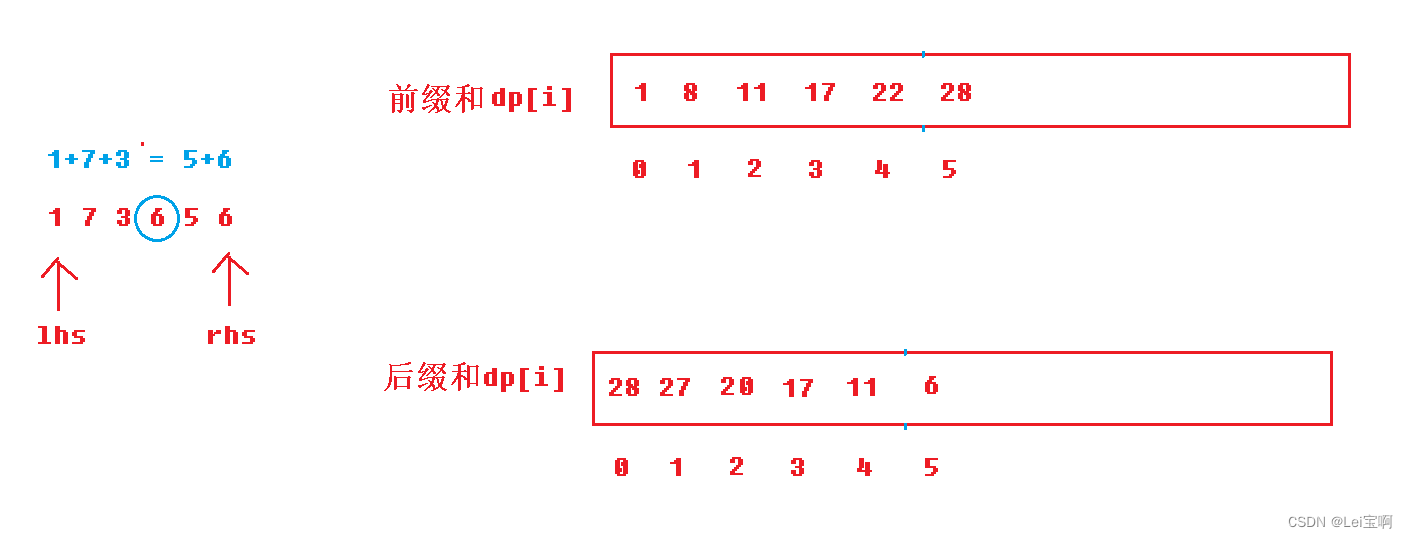
那么写成代码如何推导这两个dp表呢？

dp[i]是下标0到下标i-1的和，dp[i-1]是下标0到下标i-2元素的和......,dp[1]就是dp[0]加上下标为0元素的值，dp[0]我们初始化为0。因为题目规定下标为0或者右边的边界时，左边元素和，右边元素和为0，所以我们dp[0],dp[n-1]初始化为0。

我们写成公式就是

• 前缀 dp[i] =  dp[i-1] + nums[i-1]，i从1开始
• 后缀 dp[i] = dp[i+1] + nums[i+1]，i从n-2开始 

使用dp表计算

我们使前缀dp[i] 与 后缀dp[i]做比较，相等则返回下标，循环外则返回-1。

解题源码

class Solution 
{
public:int pivotIndex(vector<int>& nums){int n = nums.size();vector<int> f(n, 0);vector<int> g(n, 0);for (int i = 1; i < n; i++)f[i] = f[i - 1] + nums[i - 1];for (int i = n - 2; i >= 0; i--)g[i] = g[i + 1] + nums[i + 1];for (int i = 0; i < n; i++){if (f[i] == g[i])return i;}return -1;}
};

其实博主个人感觉方法一好理解一点，不过方法二的思想值得我们去学习，同时不要死记前缀和，后缀和公式，dp[i]的情况是不同的，就像我们的方法一和方法二，他们中的dp[i]含义就不同，我们需要理解的是思想。