当前位置： 首页 > news >正文

TIA博途中通过SCL语言实现快速排序的具体方法示例

news 2026/2/2 13:52:40

TIA博途中通过SCL语言实现快速排序的具体方法示例

0.1
0.2

首先，了解一下快速排序的原理：

排序算法的思想非常简单，在待排序的数列中，我们首先要找一个数字作为基准数。为了方便，我们一般选择第 1 个数字作为基准数（其实选择第几个并没有关系）。接下来我们需要将这个待排序的数列中小于基准数的元素移动到待排序的数列的左边，把大于基准数的元素移动到待排序的数列的右边。这时，左右两个分区的元素就相对有序了；接着把两个分区的元素分别按照上面两种方法继续对每个分区找出基准数，然后移动，直到各个分区只有一个数时为止。

下面和大家分享如何在TIA博途中用SCL语言来实现：

如下图所示，新建一个项目，添加一个FC块，名为：data_Swap，该块的接口变量定义如右侧所示，该FC块的功能是实现数据位置的交换，为后续的快速排序做准备，
1

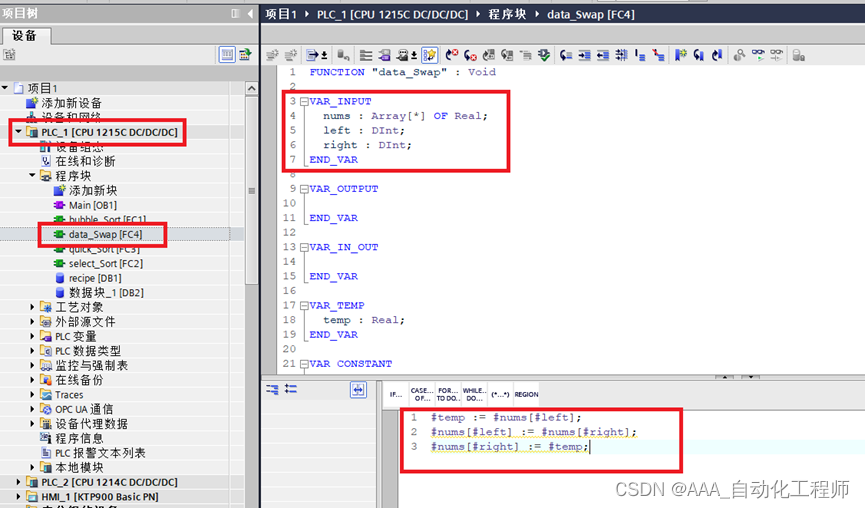
如下图

相关文章：

TIA博途中通过SCL语言实现快速排序的具体方法示例

TIA博途中通过SCL语言实现快速排序的具体方法示例 首先，了解一下快速排序的原理： 排序算法的思想非常简单，在待排序的数列中，我们首先要找一个数字作为基准数。为了方便，我们一般选择第 1 个数字作为基准数（其实选择第几个并没有关系）。接下来我们需要将这个待排序的数列…...

编程日记 2023/3/3 23:57:37

第 46 届世界技能大赛浙江省选拔赛“网络安全“项目B模块任务书

第46届世界技能大赛浙江省选拔赛"网络安全"项目B模块（网络安全事件响应、数字取证调查）第46届世界技能大赛浙江省选拔赛"网络安全"项目B模块2.1 第一部分 事件响应2.2 第二部分 数字取证调查2.3 第三部分 应用程序安全第46届世界技能…...

编程日记 2023/3/3 23:56:16

【C】字符串操作函数

初始化字符串 #include <string.h>void *memset(void *s, int c, size_t n); 返回值&#xff1a;s指向哪&#xff0c;返回的指针就指向哪memset函数把s所指的内存地址开始的n个字节都填充为c的值。通常c的值为0&#xff0c;把一块内存区清零。例如定义char buf[10];&…...

编程日记 2023/3/3 23:55:06

【python】 pytest自动化测试框架--selenium，requests，appium自动化工具

一、pytest简介 pytest是python的一种单元测试框架&#xff0c;与python自带的unittest测试框架类似&#xff0c;但是比unittest框架使用起来更简洁&#xff0c;效率更高 二、 pytest 单元测试框架 1、pytest 特点 pytest是python当中的一个单元框架&#xff0c;比unittest更灵…...

编程日记 2023/3/3 23:53:36

Spring boot 实战指南（三）：配置事务，整合Elasticsearch、swagger、redis、rabbitMQ

文章目录一、配置事务依赖使用注解二、Elasticsearch创建项目配置maven完善依赖es连接配置实体映射repositoryservicecontroller三、swagger依赖启动类路径匹配配置配置类controller注解四、redis&#xff08;代码实现&#xff09;依赖yml配置配置类封装redisTamplate五、rabbi…...

编程日记 2023/3/3 23:52:21

九、Bean的循环依赖问题

1 什么是Bean的循环依赖 A对象中有B属性。B对象中有A属性。这就是循环依赖。我依赖你&#xff0c;你也依赖我。 比如&#xff1a;丈夫类Husband&#xff0c;妻子类Wife。Husband中有Wife的引用。Wife中有Husband的引用。 2 singleton下的set注入产生的循环依赖 丈夫类 pac…...

编程日记 2023/3/3 23:51:08

macOS关闭SIP后，仍无法修改/usr文件夹下文件

发现问题 MacOS 升级到Big Sur后&#xff0c;删除多余的python3文件&#xff0c;发现写不到磁盘&#xff0c;会报OSError: [Errno 30] Read-only file system的错误。经过了解&#xff0c;在Mac OS10.11 之后&#xff0c;苹果公司为了提高系统环境安全&#xff0c;引入了一个内…...

编程日记 2023/3/3 23:49:55

【编程基础之Python】8、Python复合数据类型

【编程基础之Python】8、Python复合数据类型Python复合数据类型列表&#xff08;List&#xff09;创建列表访问元素内置方法列表操作元组&#xff08;Tuple&#xff09;创建元组访问元素集合&#xff08;Set&#xff09;创建集合基本操作其他操作字典&#xff08;Dictionary&am…...

编程日记 2023/3/3 23:48:32

自动驾驶决策规划-控制方向学习资料总结（附相关资料的链接）

项目仓库 欢迎访问我的Github主页 项目名称说明chhCpp学习C仓库chhRobotics学习自动驾驶、控制理论相关仓库(python实现)chhRobotics_CPP学习自动驾驶、控制理论相关仓库(c实现)chhML 、chh-MachineLearning学习机器学习仓库chhRL学习强化学习仓库chhTricks存放一些有意思的t…...

编程日记 2023/3/3 23:47:05

网络安全岗位介绍——售前工程师

一、工作内容 1、独立完成并配合销售人员引导客户完成方案设计、产品选型、配置报价和能为客户提供安全咨询与方案优化等服务; 2、作为售前工程师&#xff0c;跟踪整个项目的进展&#xff0c;和销售进行配合&#xff0c;协调公司各种资源完成项目中标; 3、编写投标文件的技术…...

编程日记 2023/3/3 23:45:53

nodejs安装和卸载超详细步骤

安装程序①下载完成后&#xff0c;双击安装包&#xff0c;开始安装&#xff0c;使用默认配置安装一直点next即可&#xff0c;安装路径默认在C:\Program Files下&#xff0c;也可以自定义修改②安装路径默认在C:\Program Files下面&#xff0c;也能够自定义修改&#xff0c;而后…...

编程日记 2023/3/3 23:44:35

【Leetcode】移除链表元素 链表的中间节点 链表中倒数第k个节点

目录 一.【Leetcode203】移除链表元素 1.链接 2.题目再现 A.双指针法 B.类尾删法 C.哨兵位 二.【Leetcode876】链表的中间节点 1.链接&#xff1a;链表的中间节点 2.题目再现 3.解法&#xff1a;快慢指针 三.链表中倒数第k个节点 1.链接&#xff1a;链表中倒数第k个…...

编程日记 2023/3/3 23:43:09

快速上手配置firewalld

firewalld使用firewall-cmd命令配置策略。 查看当前firewalld当前服务运行状态 firewall-cmd --state firewalld防火墙状态还用使用如下命令查看状态 systemctl status firewalld 查看所有打开运行的端口 firewall-cmd --zonepublic --list-ports 查看区域信息情况 firewall…...

编程日记 2023/3/3 23:41:46

treap使用mt19937会导致问题原因分析

Treap 是一种使用随机数生成器来维护树形结构的数据结构&#xff0c;而 mt19937 是一种常用的伪随机数生成器。虽然 mt19937 可以生成高质量的随机数序列&#xff0c;但是在 Treap 中使用它可能会导致一些问题。 mt19937 返回的是一个 unsigned int 其中一个问题是&#xff0…...

编程日记 2023/3/3 23:40:22

tmux和vim

tmux 作用 分屏 允许断开Terminal连接后继续运行进程 结构 一个tmux可以开一堆session tmux: session 1, session 2, session 3 … Session: window 1, window 2, window 3… Window: pane 1, pane 2, pane 3… pane是最小单位&#xff0c;用shell语言编程 操作 输入…...

编程日记 2023/3/3 23:37:51

2023年全国最新保安员精选真题及答案12

百分百题库提供保安员考试试题、保安职业资格考试预测题、保安员考试真题、保安职业资格证考试题库等&#xff0c;提供在线做题刷题&#xff0c;在线模拟考试&#xff0c;助你考试轻松过关。 121.《保安员证》是经由设区的&#xff08;&#xff09;单位进行发放。 A:市级人民政…...

编程日记 2023/3/3 23:36:06

Hbase的基本概念与架构

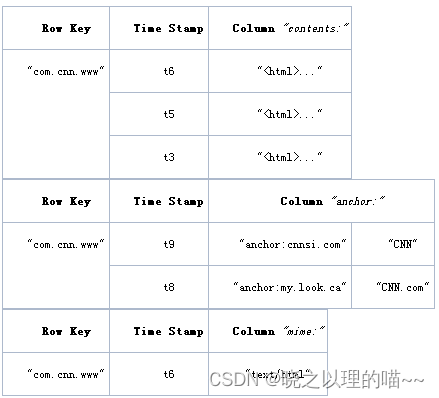
一、Hbase的概念 HBase是Hadoop的生态系统&#xff0c;是建立在Hadoop文件系统&#xff08;HDFS&#xff09;之上的分布式、面向列的数据库&#xff0c;通过利用Hadoop的文件系统提供容错能力。如果你需要进行实时读写或者随机访问大规模的数据集的时候&#xff0c;请考虑使用H…...

编程日记 2023/3/3 23:34:48

颠覆你的认知，业务同事都能开发软件，我简直无地自容……

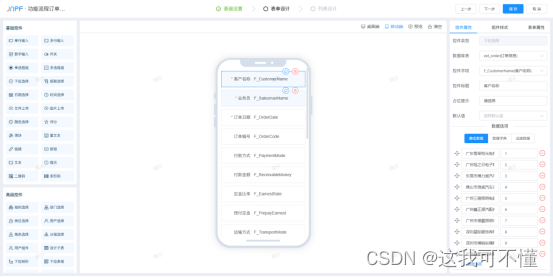
经常看到网络鼓吹业务人员也能搭建应用&#xff0c;本是嗤之以鼻、半信半疑&#xff0c;但当这件事真实发生在自己身上时&#xff0c;竟觉得此言不虚&#xff1f; 一、背景 最近公司为了集成系统、提升扩展能力&#xff0c;引进了低代码平台JNPF&#xff0c;说个题外话&#…...

编程日记 2023/3/3 23:33:33

01 | n2n虚拟局域网

1 n2n简介 为了满足两个不同局域网的机器进行通信&#xff0c;让不同网段的机器能够进行P2P( 点对点 peer-to-peer ) 通信。2 n2n源码 https://github.com/ntop/n2n.git3 n2n名词 3.1 SuperNode 超级节点 SuperNode 相当与注册中心, 它会记录边缘节点的连接信息&#xff0c;…...

编程日记 2023/3/3 23:32:20

MFC界面控件BCGControlBar v33.4 - 支持Win 11 Mica material主题

BCGControlBar库拥有500多个经过全面设计、测试和充分记录的MFC扩展类。 我们的组件可以轻松地集成到您的应用程序中&#xff0c;并为您节省数百个开发和调试时间。BCGControlBar专业版和BCGSuite for MFC v33.4已正式发布了&#xff0c;该版本包含了对Windows 11 Mica materia…...

编程日记 2023/3/3 23:31:05

golang循环变量捕获问题​​

在 Go 语言中&#xff0c;当在循环中启动协程&#xff08;goroutine&#xff09;时&#xff0c;如果在协程闭包中直接引用循环变量&#xff0c;可能会遇到一个常见的陷阱 - ​​循环变量捕获问题​​。让我详细解释一下&#xff1a; 问题背景 看这个代码片段&#xff1a; fo…...

编程新知 2026/1/21 14:29:57

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能

下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能&#xff0c;包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

编程新知 2025/11/14 9:31:35

Admin.Net中的消息通信SignalR解释

定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

编程新知 2025/9/10 5:36:56

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖

在前面的练习中&#xff0c;每个页面需要使用ref&#xff0c;onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入&#xff0c;需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

编程新知 2025/9/14 18:41:15

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表

1、行为树节点分类 在 Nav2（Navigation2）的行为树框架中，行为树节点插件按照功能分为 Action（动作节点）、Condition（条件节点）、Control（控制节点） 和 Decorator（装饰节点） 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务，直接与硬件、传感器或外部系统…...

编程新知 2026/1/29 4:00:56

React19源码系列之 事件插件系统

事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

编程新知 2026/1/30 5:56:27

C++ 求圆面积的程序（Program to find area of a circle）

给定半径r&#xff0c;求圆的面积。圆的面积应精确到小数点后5位。 例子&#xff1a; 输入&#xff1a;r 5 输出&#xff1a;78.53982 解释&#xff1a;由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982&#xff0c;因为我们只保留小数点后 5 位数字。 输…...

编程新知 2026/1/31 12:52:15

Java 二维码

Java 二维码 **技术&#xff1a;**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

编程新知 2025/9/6 16:22:45

uniapp手机号一键登录保姆级教程（包含前端和后端）

目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号&#xff08;第三种&#xff09;后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

编程新知 2026/1/27 2:03:36

Python Einops库：深度学习中的张量操作革命

Einops&#xff08;爱因斯坦操作库&#xff09;就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库&#xff0c;用类似自然语言的表达式替代了晦涩的API调用&#xff0c;彻底改变了深度学习工程…...

编程新知 2025/10/16 12:04:52