代码随想录算法训练营Day18|513.找树左下角的值、112. 路径总和、113. 路径总和ii、106.从中序与后序遍历序列构造二叉树
目录
513.找树左下角的值
前言
层序遍历
递归法
112. 路径总和
前言
递归法
113. 路径总和ii
前言
递归法
106.从中序与后序遍历序列构造二叉树
前言
思路
递归法
总结
513.找树左下角的值
题目链接
文章链接
前言
本题要求得到二叉树最后一行最左边的值,使用层序遍历可以较为容易地实现,使用递归法要再次用到回溯对不满足条件的路径进行回退。
层序遍历
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int findBottomLeftValue(TreeNode* root) {queue<TreeNode*> que;int result = 0;if (root == NULL) return result;que.push(root);vector <int> vec;while (!que.empty()){int size = que.size();vec = {}; //每层遍历都要初始化vec数组for (int i = 0; i < size; i++){TreeNode* node = que.front();que.pop();vec.push_back(node->val);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return result = vec[0];}
};因为最终只要获得最后一行的节点数值,所以vec容器每层都要重新初始化进行收集,直到最后一层,此时容器中保存的即为最后一行的节点数值,第一个就是符合条件的左下角的值。
递归法
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int maxDepth = INT_MIN;int result;void traversal(TreeNode* root, int depth){if (root->left == NULL && root->right == NULL){ //判断是否为叶子节点if (depth > maxDepth){maxDepth = depth;result = root->val;}return;}if (root->left){ //左depth++;traversal(root->left, depth);depth--; //回溯}if (root->right){ //右depth++;traversal(root->right,depth);depth--; //回溯}return;}int findBottomLeftValue(TreeNode* root) {traversal(root, 0);return result;}
};由于只需要求最下行最左侧节点,因此在递归遍历时不需要对中节点进行处理,满足最大深度的叶子节点和最左侧的条件才是符合题目要求的。
112. 路径总和
题目链接
文章链接
前言
本题的目的在于更好地理解递归函数什么时候要有返回值,什么时候没有返回值。
在确定递归函数的参数和返回类型时,参数需要二叉树的根节点,还需要一个计数器,这个计数器用来计算二叉树的一条边之和是否正好是目标和,计数器为int型。
递归函数什么时候需要返回值?什么时候不需要返回值?这里总结如下三点:
- 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。
- 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。
- 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。
递归法
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool traversal(TreeNode* cur, int count){if (!cur->left && !cur->right && count == 0) return true;if (!cur->left && !cur->right) return false;if (cur->left){count -= cur->left->val;if (traversal(cur->left, count)) return true;count += cur->left->val; //回溯}if (cur->right){count -= cur->right->val;if (traversal(cur->right, count)) return true;count += cur->right->val;}return false;}bool hasPathSum(TreeNode* root, int targetSum) {if (root == NULL) return false;return traversal(root, targetSum - root->val);}
};掌握本题后,下面一题就好理解了。
113. 路径总和ii
题目链接
文章链接
前言
路径总和ii要遍历整个树,找到所有路径,所以递归函数不要返回值!
递归法
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:vector<vector<int>> result;vector<int> path;void traversal(TreeNode* cur, int count){if (!cur->left && !cur->right && count == 0){result.push_back(path);return;}if (!cur->left && !cur->right) return;if (cur->left){path.push_back(cur->left->val); count -= cur->left->val;traversal(cur->left, count);count += cur->left->val;path.pop_back();}if (cur->right){path.push_back(cur->right->val);count -= cur->right->val;traversal(cur->right, count);count += cur->right->val;path.pop_back();}return;}public:vector<vector<int>> pathSum(TreeNode* root, int targetSum) {if (root == NULL) return result;path.push_back(root->val);traversal(root, targetSum - root->val);return result;}
};106.从中序与后序遍历序列构造二叉树
题目链接
文章链接
前言
本题要根据两个遍历顺序构造一个唯一的二叉树,整体思路是以后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
思路
实现步骤:
-
第一步:判断数组大小是否为零,为零说明是空节点了;
-
第二步:如果不为零,那么取后序数组最后一个元素作为根节点元素;
-
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点;
-
第四步:切割中序数组,切成中序左数组和中序右数组 ;
-
第五步:切割后序数组,切成后序左数组和后序右数组;
-
第六步:递归处理左区间和右区间
递归法
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:TreeNode* traversal(vector<int>& inorder, vector<int>& postorder){//第一步 判断数组是否为空节点if (postorder.size() == 0) return NULL;//第二步 后序遍历数组最后一个元素 就是二叉树的中间节点(根节点)int rootValue = postorder[postorder.size() - 1];TreeNode* root = new TreeNode(rootValue);//根节点即为叶子节点时if (postorder.size() == 1) return root;//第三步 找切割点int index;for (index = 0; index < inorder.size(); index++){if (inorder[index] == rootValue) break;} //第四步 切割中序数组 得到 中序左数组和中序右数组//左闭右开区间vector<int> leftInorder(inorder.begin(), inorder.begin() + index);vector<int> rightInorder(inorder.begin() + index + 1, inorder.end());//第五步 切割后序数组 得到 后序左数组和后序右数组postorder.resize(postorder.size() - 1);vector<int>leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());vector<int>rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());//第六步递归处理左区间和右区间root->left = traversal(leftInorder, leftPostorder);root->right = traversal(rightInorder, rightPostorder);return root;}public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if (inorder.size() == 0) return NULL;return traversal(inorder, postorder);}
};要注意切割时边界值的判断。
总结
重点掌握巩固二叉树的递归实现,以及二叉树递归参数及返回值的确定。
相关文章:

代码随想录算法训练营Day18|513.找树左下角的值、112. 路径总和、113. 路径总和ii、106.从中序与后序遍历序列构造二叉树
目录 513.找树左下角的值 前言 层序遍历 递归法 112. 路径总和 前言 递归法 113. 路径总和ii 前言 递归法 106.从中序与后序遍历序列构造二叉树 前言 思路 递归法 总结 513.找树左下角的值 题目链接 文章链接 前言 本题要求得到二叉树最后一行最左边的值…...

【蓝桥备赛】技能升级——二分查找
题目链接 技能升级 个人思路 需要给n个技能添加技能点,无论技能点加成如何衰减,每次始终都是选择当前技能加点加成最高的那一项技能,所以最后一次的加点一定也是加在当时技能攻击加成最高的那个。此时,我们去寻找最后一次的加点…...

zyqn-arm软中断设置
所有SGI都是边缘触发的,sgi的灵敏度类型是固定的,不能改变。 软中断初始化流程 1、初始化异常处理 2、初始化中断控制器 3、注册异常处理回调函数到CPU 4、连接软中断信号与注册软中断回调函数 5、使能中断控制器中的软中断中断 6、使能异常处理 …...

k8s---pod基础下
k8s的pod与docker重启策略的区别 k8s的重启策略 always deployment的yaml文件只能是always,pod的yaml三种模式都可以。不论正常退出还是非正常退出都重启。OnFailure:正常退出不重启,非正常退出会重启Never:正常退出和非正常退出…...
玩转朋友圈!这样运营朋友圈吸睛又吸金!
朋友圈已成为现代社交媒体中不可或缺的平台,并且有很大的潜力用于营销和推广。那么如何才能让朋友圈在众多用户中脱颖而出,吸引眼球并提升商业效益呢?主要从以下几点出发: 首先,要想吸引关注,您需要在朋友…...
react学习
目录 一、react基础 5.loadsh使用排序8.ref获取DOM对象10.props使用*13.UseEffect 二、 react使用redux三、美团外卖项目完成页面制作使用redux渲染页面使用react-router-dom评价 一、react基础 jsx 大括号的作用 {count} {userLlist.map((item)>{return <li key{item…...

vue-cli项目中vue.config.js的配置
vue-cli项目中vue.config.js的配置 一、直接上代码 一、直接上代码 let path require(path) let glob require(glob)function resolve(dir) {return path.join(__dirname, src/${dir}) }module.exports {pages: {index: {// page 的入口entry: src/main.js,// 模板来源temp…...

Github 2024-01-04 开源项目日报 Top10
根据Github Trendings的统计,今日(2024-01-04统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Python项目3C项目2TypeScript项目2Java项目2Jupyter Notebook项目1Go项目1 系统设计指南 创建周期ÿ…...

使用GPTs+Actions自动获取第三方数据
目录 安装插件与GPT对话联网插件首先,创建GPTs。 Voxscript 官网:https://voxscript.awt.icu/index.htmlOpenAI Schema:https://voxscript.awt.icu/swagger/v1/swagger.yamlServer URL: servers: url: https://voxscript.awt.icu安装插件 要使用这个插件&...

git提交操作(不包含初始化仓库)
1.进入到本地的git仓库 查看状态 git status 如果你之前有没有成功的提交,直接看第5步。 2.追踪文件 git add . 不要提交大于100M的文件,如果有,看第5步 3.提交评论 git commit -m "你想添加的评论" 4.push (push之前可以再…...
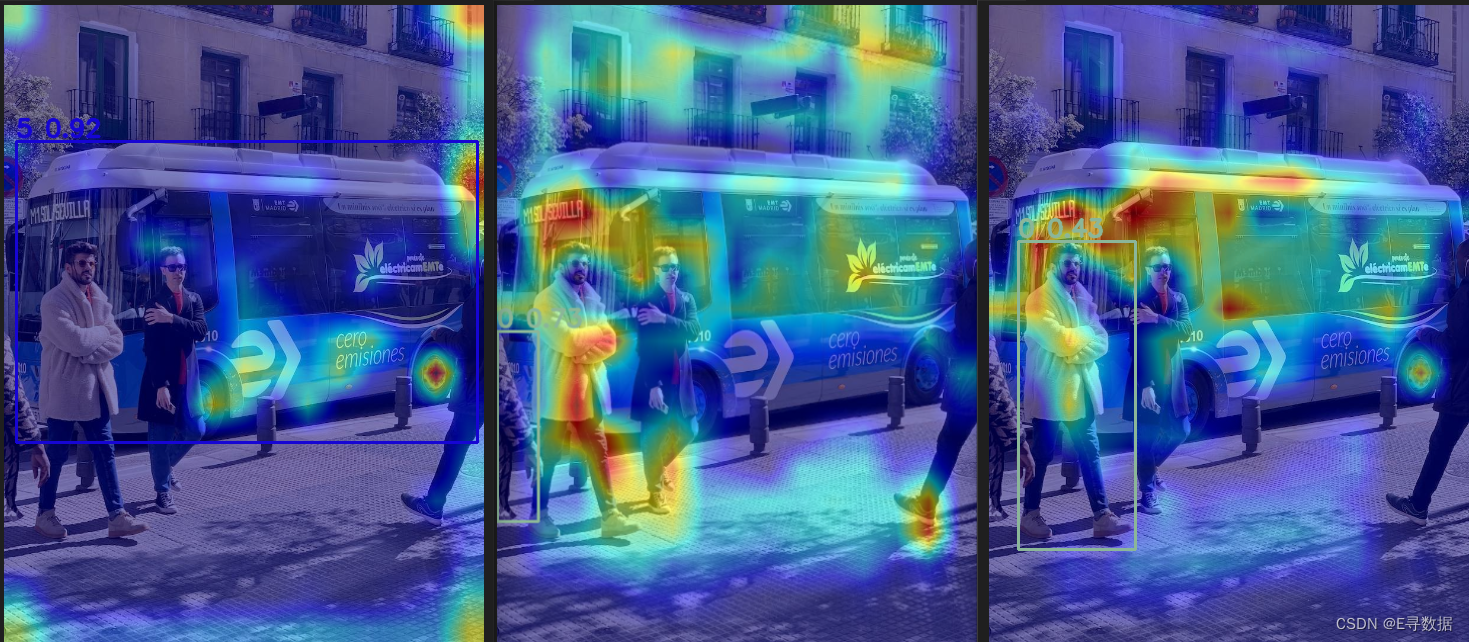
使用YOLOv8和Grad-CAM技术生成图像热图
目录 yolov8导航 YOLOv8(附带各种任务详细说明链接) 概述 环境准备 代码解读 导入库 定义letterbox函数 调整尺寸和比例 计算填充 应用填充 yolov8_heatmap类定义和初始化 后处理函数 绘制检测结果 类的调用函数 热图生成细节 参数解释 we…...
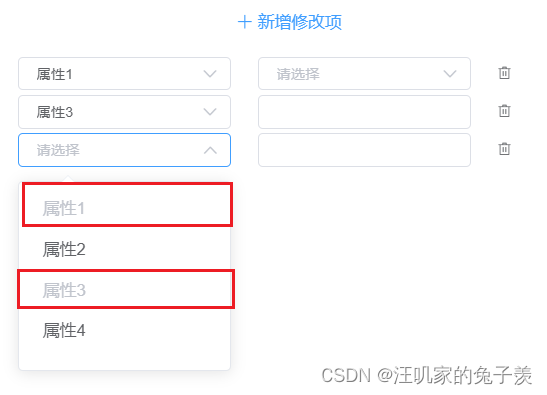
Vue: 多个el-select不能重复选择相同属性
一、场景 1.需求: 用户可自由选择需要修改的对象并同时修改多个属性,需要校验修改对象不能重复选择,但是可供修改属性是固定的 2.目标效果: 二、实现 1.主要代码: <template><el-selectv-model"se…...

金色麦芒的2023
2023年即将过去,回首这一年,我深感自己在技术和职业生涯中取得了巨大的进步。这一年里,我不仅在技术层面有了更深入的掌握,也在个人成长和职业规划上有了更明确的方向。 首先,在技术层面,我今年最大的收获是…...

java设计模式学习之【策略模式】
文章目录 引言策略模式简介定义与用途实现方式 使用场景优势与劣势在Spring框架中的应用计算示例代码地址 引言 设想你正在玩一个策略游戏,每一个决策都会导致不同的游戏结局。同样地,在软件开发中,我们常常需要根据不同的场景或条件选择不同…...
)
Mybatis SQL构建器类 - SqlBuilder and SelectBuilder (已经废弃)
在3.2版本之前,我们采用了一种略有不同的方法,通过利用ThreadLocal变量来掩盖一些使Java DSL有点繁琐的语言限制。然而,这种方法现在已被弃用,因为现代框架已经普及了使用构建器模式和匿名内部类的概念。因此,SelectBu…...

【Linux】不常用命令记录
查看开启的网络端口 1、使用netstat命令“netstat -tuln”,该命令将显示所有当前监听的TCP和UDP端口; 2、使用ss命令“ss -tuln”,用于显示当前监听的TCP和UDP端口; 3、使用lsof命令“lsof -i”,将显示当前打开的网络…...

【docker】安装docker环境并启动容器
一、安装docker 这里以centos系统为例安装docker环境 # 删除已有安装包 sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotate \docker-enginesudo yum install -y yum-utils # 设置源 y…...
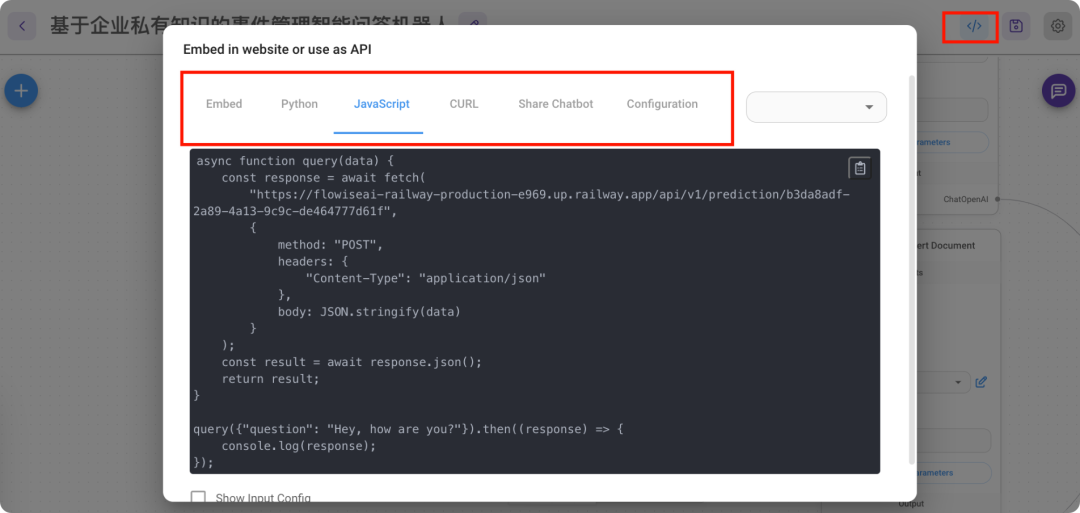
AIOps探索 | 基于大模型构建高效的运维知识及智能问答平台(2)案例分享
原作者:擎创科技产品专家 布博士 案例分享 所需要的软件列表 本次案例的实现,全部采用开源或SAAS的产品来提供,并不涉及到私有化部署的软件产品。软件列表如下所示,如何申请apikey请自行研究,在这里不再详细说明&…...
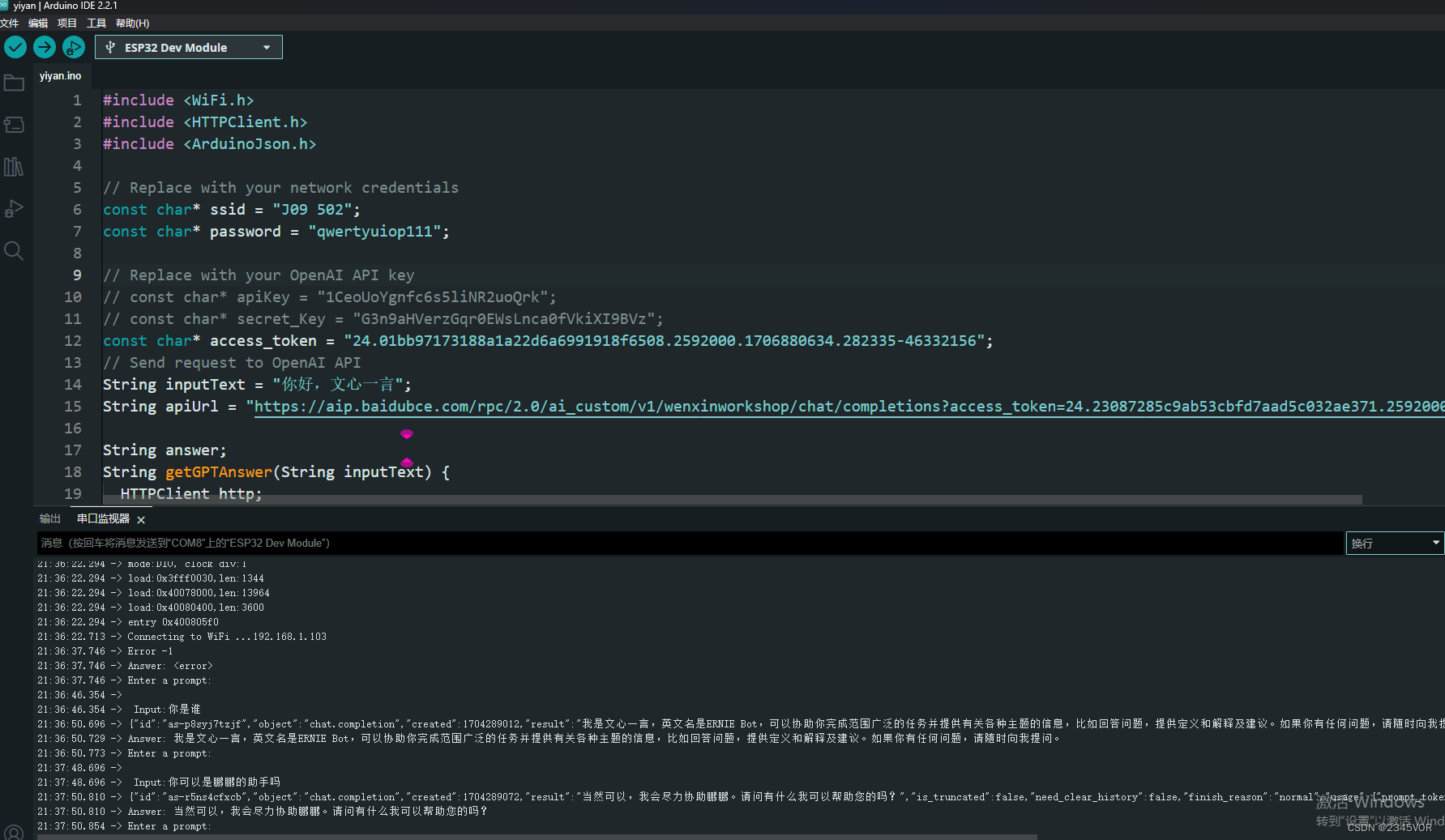
【ESP32接入国产大模型之文心一言】
1. 怎样接入文心一言 随着人工智能技术的不断发展,自然语言处理领域也得到了广泛的关注和应用。在这个领域中,文心一言作为一款强大的自然语言处理工具,具有许多重要的应用价值。本文将重点介绍如何通过ESP32接入国产大模型之文心一言api&am…...
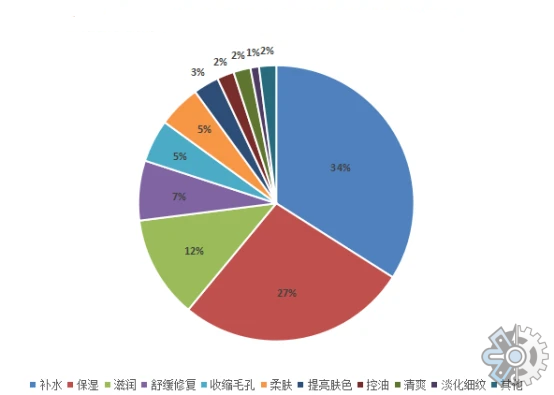
保湿剂,预计2026年市场规模将达到约230亿美元
全球市场分析 从全球市场来看,保湿剂市场规模正在快速增长。主要集中在欧美和亚太地区的市场,据市场调研机构的数据显示,预计2026年,全球保湿剂市场规模将达到约230亿美元。保湿剂的应用领域不断拓展,包括从化妆品到个…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
