数据结构:第7章:查找(复习)
目录
顺序查找:
折半查找:
二叉排序树:
4. (程序题)
平衡二叉树:
顺序查找:
ASL=
折半查找:
这里 j 表示 二叉查找树的第 j 层
二叉排序树:
二叉排序树(Binary Search Tree,BST)是一种特殊的二叉树,定义:
- 对于二叉排序树的每个节点,其左子树的所有节点的值都小于该节点的值。
- 对于二叉排序树的每个节点,其右子树的所有节点的值都大于该节点的值。
- 对于二叉排序树的每个节点,其左右子树也分别是二叉排序树。
可以发现二叉排序树的定义时递归定义。
这些性质保证了对于二叉排序树中的任意节点,其左子树的节点值小于它,右子树的节点值大于它,从而形成了一种有序的结构。
二叉排序树的有序性质使得在其中进行查找、插入和删除等操作时具有较高的效率。对于给定的值,可以通过比较节点的值,按照二叉排序树的性质在树中快速定位所需的节点。
二叉排序树的难点在于删除树中的某个值。删除某个键值为 key 的节点时,有三中情况要考虑:
1.该节点 r 的左孩子为空:r=r->lch;
2.该节点 r 的右孩子为空:l=l->rch;
3.该节点的左右孩子均不位空:选择左孩子中 key 值最大的节点替换 r;
4. (程序题)
二叉排序树插入、删除
键盘输入若干整型数据,以0做结束,利用二叉排序树的插入算法创建二叉排序树,并中序遍历该二叉树。之后输入一个整数x,在二叉排序树中查找,若找到则输出“该数存在”,否则输出“该数不存在”;再输入一个要删除的一定存在的整数y,完成在该二叉树中删除y的操作,并输出删除y后的二叉树中序遍历的结果。
输出数据之间用一个空格分隔。
输入:
1 5 4 2 3 6 8 7 9 11 14 13 12 16 19 0
输出:
1 2 3 4 5 6 7 8 9 11 12 13 14 16 19
输入:
19
输出:
该数存在
输入:
14
输出:
1 2 3 4 5 6 7 8 9 11 12 13 16 19
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
using namespace std;
typedef long long LL;typedef struct Info {int key;
}Info;typedef struct Node {Info data;struct Node* lch;struct Node* rch;
}Node,*Tree;void print(Tree& r) {if (r == NULL)return;print(r->lch);cout << r->data.key << " ";print(r->rch);
}void Insert(Tree& r, int key) {if (r == NULL) {Node* p = new Node;p->data.key = key;p->rch = p->lch = NULL;r = p;}else if(r->data.key<key) {Insert(r->rch, key);}else {Insert(r->lch, key);}
}void build(Tree& r) {int in;cin >> in;while (in) {Insert(r, in);cin >> in;}
}int search(Tree& r, int key) {if (r == NULL)return 0;if (r->data.key == key) {return 1;}if (r->data.key < key) {if (search(r->rch, key))return 1;}else {if (search(r->lch, key))return 1;}return 0;
}int del(Tree& r, int key) {if (r == NULL)return 0;if (r->data.key == key) {if (r->lch == NULL) {r =r->rch;}else if (r->rch == NULL) {r =r->lch;}else {//cout << r->data.key << endl;Node* p = r->lch;Node* fa = r;while (p->rch != NULL) {fa = p;p = p->rch;}Node* t = r;if (fa != r)fa->rch = p->lch;if (r->lch != p)p->lch = r->lch;p->rch = r->rch;//cout << p->data.key << endl;r = p;delete t;}return 1;}if (r->data.key < key) {if (del(r->rch, key))return 1;}else {if (del(r->lch, key))return 1;}return 0;
}int main() {Node* root = NULL;build(root);print(root);int in;cin >> in;if (search(root, in)) {cout << "该数存在" << endl;}else {cout << "该数不存在" << endl;}cin >> in;del(root, in);print(root);return 0;
}用例1:
输入
1 5 4 2 3 6 8 7 9 11 14 13 12 16 19 0 19 14
输出
1 2 3 4 5 6 7 8 9 11 12 13 14 16 19 该数存在 1 2 3 4 5 6 7 8 9 11 12 13 16 19
用例2:
输入
10 9 8 7 11 12 13 14 0 14 8
输出
7 8 9 10 11 12 13 14 该数存在 7 9 10 11 12 13 14
用例3:
输入
23 45 67 21 12 15 9 10 55 0 19 9
输出
9 10 12 15 21 23 45 55 67 该数不存在 10 12 15 21 23 45 55 67
平衡二叉树:
平衡二叉树的定义
平衡二叉排序树查找算法的性能取决于二叉树的结构,而二叉树的形状则取决于其数据集。
如果数据呈有序排列,则二叉排序树是线性的,查找的时间复杂度为O(n);反之,如果二叉排序
树的结构合理,则查找速度较快,查找的时间复杂度为O(logn)。事实上,树的高度越小,查找
速度越快。因此,希望二叉树的高度尽可能小。本节将讨论一种特殊类型的二叉排序树,称为平
衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree),因由前苏联数学家 Adelson-Velskii 和
Landis 提出,所以又称AVL树。
平衡二叉树或者是空树,或者是具有如下特征的二叉排序树:
(1)左子树和右子树的深度之差的绝对值不超过1;
(2)左子树和右子树也是平衡二叉树。
若将二叉树上结点的平衡因子(Balance Factor,BF)定义为该结点左子树和右子树的深度之
差,则平衡二叉树上所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡
因子的绝对值大于1,则该二叉树就是不平衡的。图7.11(a)所示为两棵平衡二叉树,而图 7.11
(b)所示为两棵不平衡的二叉树,结点中的值为该结点的平衡因子。
平衡二叉树的调整(重难点)
LL型调整操作:由于在A左子树根结点的左子树上插入结点,A的平衡因子由1增至2,致使以A为根的子树失去平衡,则需进行一次向右的顺时针旋转操作

RR 型调整操作:当在 A 的右子树的右子树上插入结点时,A 的平衡因子由 -1 变为 -2,导致以 A 为根结点的子树失去平衡。此时,需要进行一次向左的逆时针旋转操作,将 A 的右子树作为其左子树的右子树,并将 A 作为其左子树的根结点。

LR型调整操作:由于在A的左子树根结点的右子树上插入结点, A的平衡因子由1增至2,致使以A为根结点的子树失去平衡,则需进行两次旋转操作。第一次对B及其右子树进行递时针旋转,C转上去成为B的根,这时变成了LL型,所以第二次进行LL型的顺时针旋转即可恢复平衡。如果C原来有左子树,则调整C的左子树为B的右子树,
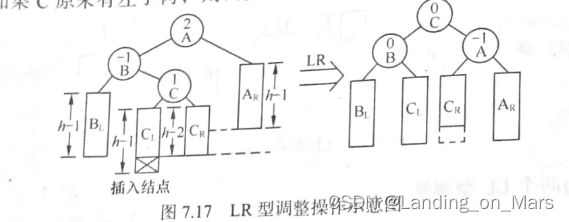
RL型调整操作:由于在A的右子树根结点的左子树上插入结点,A的平衡因子由-1变为-2,致使以A 为根结点的子树失去平衡,则旋转方法和LR型相对称,也需进行两次旋转,先顺时针右旋,再逆时针左旋。
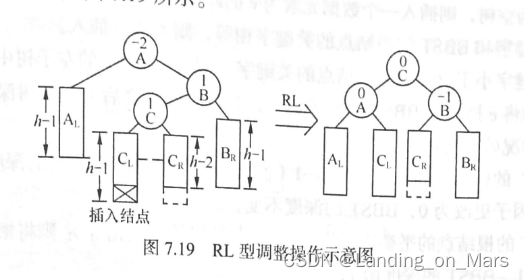
左,右旋转调整代码:mp用来记录某个节点的高度
void Turnleft(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->right;A->right = B->left;B->left = A;r = B;mp[r->left] -= 2;mp[r] = mp[r->right] + 1;}void Turnright(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->left;A->left = B->right;B->right = A;r = B;mp[r->right] -= 2;mp[r] = mp[r->left] + 1;}
判断不平衡类型类型的代码:
void fun1(vector<int>& g, TreeNode* r) {if ( r == NULL||(r->left==NULL&&r->right==NULL))return;if (mp[r->left] == mp[r->right])return;g.push_back(mp[r->left] - mp[r->right]);fun1(g, r->left);fun1(g, r->right);}string check(TreeNode* root) {vector<int>g;fun1(g, root);if (g[0] == 2&&g[1]==1)return "LL";else if (g[0] == 2&&g[1]==-1)return "LR";else {if (g[0] == -2&&g[1]==1)return "RL";return "RR";}return "NO";}建立平衡二叉树的代码
class Solution {
public:unordered_map<TreeNode*, int>mp;void fun1(vector<int>& g, TreeNode* r) {if (r == NULL || (r->left == NULL && r->right == NULL))return;if (mp[r->left] == mp[r->right])return;g.push_back(mp[r->left] - mp[r->right]);fun1(g, r->left);fun1(g, r->right);}string check(TreeNode* root) {vector<int>g;fun1(g, root);if (g[0] == 2 && g[1] == 1)return "LL";else if (g[0] == 2 && g[1] == -1)return "LR";else {if (g[0] == -2 && g[1] == 1)return "RL";return "RR";}return "NO";}void Turnleft(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->right;A->right = B->left;B->left = A;r = B;mp[r->left] -= 2;mp[r] = mp[r->right] + 1;}void Turnright(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->left;A->left = B->right;B->right = A;r = B;mp[r->right] -= 2;mp[r] = mp[r->left] + 1;}void change(TreeNode*& r, string ret) {if (ret == "LL") {Turnright(r);}else if (ret == "RR") {Turnleft(r);}else if (ret == "RL") {Turnright(r->right);Turnleft(r);}else {Turnleft(r->left);Turnright(r);}}void Insert(TreeNode*& r, int key) {if (r == NULL) {TreeNode* p = new TreeNode;p->val = key;p->left = p->right = NULL;r = p;mp[r] = 1;return ;}if (key > r->val) {Insert(r->right, key);}else {Insert(r->left, key);}mp[r] = max(mp[r->left], mp[r->right]) + 1;int h = mp[r->left] - mp[r->right];if (h == 2 || h == -2) {//cout <<" ___________________"<< r->val << endl;string ret = check(r);//cout << ret << endl;change(r, ret);/* for (unordered_map<TreeNode*, int>::iterator it = mp.begin(); it != mp.end(); it++) {if (it->first != NULL) {cout << "KKKK " << it->first->val << " " << it->second << endl;}}cout << "先 ";inorderTraversal1(r);cout << endl;cout << "中 ";inorderTraversal(r);cout << endl;*/}}TreeNode* balanceBST(TreeNode*& root,vector<int>preorder) {for (int i = 0; i <preorder.size(); i++) {Insert(root, preorder[i]);}return root;}
};完整代码:
代码中有测试样例
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
using namespace std;// Definition for a binary tree node.
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};// Function to insert a value into BST
TreeNode* insertIntoBST(TreeNode* root, int val) {if (!root) {return new TreeNode(val);}if (val < root->val) {root->left = insertIntoBST(root->left, val);}else {root->right = insertIntoBST(root->right, val);}return root;
}// Function to construct BST from preorder traversal
TreeNode* bstFromPreorder(vector<int>& preorder) {TreeNode* root = nullptr;for (int val : preorder) {if (val == 0)continue;root = insertIntoBST(root, val);}return root;
}// Function to perform inorder traversal (for verification)
void inorderTraversal(TreeNode* root) {if (root) {inorderTraversal(root->left);cout << root->val << " ";inorderTraversal(root->right);}
}
void inorderTraversal1(TreeNode* root) {if (root) {cout << root->val << " ";inorderTraversal1(root->left);inorderTraversal1(root->right);}
}// Function to perform level order traversal
void levelOrderTraversal(TreeNode* root) {if (!root) {return;}queue<TreeNode*> q;q.push(root);while (!q.empty()) {TreeNode* current = q.front();q.pop();cout << current->val << " ";if (current->left) {q.push(current->left);}if (current->right) {q.push(current->right);}}
}class Solution {
public:unordered_map<TreeNode*, int>mp;void fun1(vector<int>& g, TreeNode* r) {if (r == NULL || (r->left == NULL && r->right == NULL))return;if (mp[r->left] == mp[r->right])return;g.push_back(mp[r->left] - mp[r->right]);fun1(g, r->left);fun1(g, r->right);}string check(TreeNode* root) {vector<int>g;fun1(g, root);if (g[0] == 2 && g[1] == 1)return "LL";else if (g[0] == 2 && g[1] == -1)return "LR";else {if (g[0] == -2 && g[1] == 1)return "RL";return "RR";}return "NO";}void Turnleft(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->right;A->right = B->left;B->left = A;r = B;mp[r->left] -= 2;mp[r] = mp[r->right] + 1;}void Turnright(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->left;A->left = B->right;B->right = A;r = B;mp[r->right] -= 2;mp[r] = mp[r->left] + 1;}void change(TreeNode*& r, string ret) {if (ret == "LL") {Turnright(r);}else if (ret == "RR") {Turnleft(r);}else if (ret == "RL") {Turnright(r->right);Turnleft(r);}else {Turnleft(r->left);Turnright(r);}}void Insert(TreeNode*& r, int key) {if (r == NULL) {TreeNode* p = new TreeNode;p->val = key;p->left = p->right = NULL;r = p;mp[r] = 1;return ;}if (key > r->val) {Insert(r->right, key);}else {Insert(r->left, key);}mp[r] = max(mp[r->left], mp[r->right]) + 1;int h = mp[r->left] - mp[r->right];if (h == 2 || h == -2) {//cout <<" ___________________"<< r->val << endl;string ret = check(r);//cout << ret << endl;change(r, ret);/* for (unordered_map<TreeNode*, int>::iterator it = mp.begin(); it != mp.end(); it++) {if (it->first != NULL) {cout << "KKKK " << it->first->val << " " << it->second << endl;}}cout << "先 ";inorderTraversal1(r);cout << endl;cout << "中 ";inorderTraversal(r);cout << endl;*/}}TreeNode* balanceBST(TreeNode*& root,vector<int>preorder) {for (int i = 0; i <preorder.size(); i++) {Insert(root, preorder[i]);}return root;}
};int main() {vector<int> preorder = { 1,2,3,4,5,6,7,8,9,10,31,25,47,16,28,30 };/*1,2,3,4,5,6,7,8,9,1019,10,4,17,531,25,47,40,69,43 1,2,3,4 31,25,47,40,69,36 31,25,47,16,28,26 31,25,47,16,28,30 1,2,3,4,5,6,7,8,9,10,31,25,47,16,28,30*/TreeNode* root = NULL;Solution solve;solve.balanceBST(root,preorder);levelOrderTraversal(root);cout << endl;cout << "先 ";inorderTraversal1(root);cout << endl;cout << "中 ";inorderTraversal(root);cout << endl;return 0;
}
相关文章:

数据结构:第7章:查找(复习)
目录 顺序查找: 折半查找: 二叉排序树: 4. (程序题) 平衡二叉树: 顺序查找: ASL 折半查找: 这里 j 表示 二叉查找树的第 j 层 二叉排序树: 二叉排序树(Binary Search Tree&…...

编程语言的未来?
编程语言的未来? 随着科技的飞速发展,编程语言在计算机领域中扮演着至关重要的角色。它们是软件开发的核心,为程序员提供了与机器沟通的桥梁。那么,在技术不断进步的未来,编程语言的走向又将如何呢? 在技…...

SpringBoot的测试
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开心好久好久😎 📚系列专栏:Java全栈,…...

C++睡眠函数:Windows平台下的Sleep函数和Linux平台的usleep函数
C/C睡眠函数:Windows平台下的Sleep函数和Linux平台的usleep函数 WinAPI Sleep Sleep函数属于Windows API,使用它需要先包含synchapi.h。 void Sleep(DWORD dwMilliseconds);函数仅有一个参数(睡眠时长),单位是毫秒。…...

详解白帽子以及红队、蓝队和紫队
企业继续数字化,其关键基础设施和运营扩大了攻击面,暴露于各种威胁途径的面前。为了解决这个问题,企业领导者认识到拥有内部专家的重要性。考虑到网络威胁领域不断发展的态势,企业领导者可以利用道德黑客以及红队、蓝队和紫队的工…...

1、docker常用技巧:docker数据位置更改
目录 🍅点击这里查看所有博文 随着自己工作的进行,接触到的技术栈也越来越多。给我一个很直观的感受就是,某一项技术/经验在刚开始接触的时候都记得很清楚。往往过了几个月都会忘记的差不多了,只有经常会用到的东西才有可能真正记…...

Qt之设置QLabel的背景色和前景色
方法有两种,一种是使用调色板,一种是使用样式表。 方法一:调色板 QPalette palette ; // 设置黑底绿字 palette .setColor(QPalette::Background, Qt::black); palette .setColor(QPalette::WindowText, Qt::green); // 这句不能少,否则没效果 ui->label->setAutoF…...
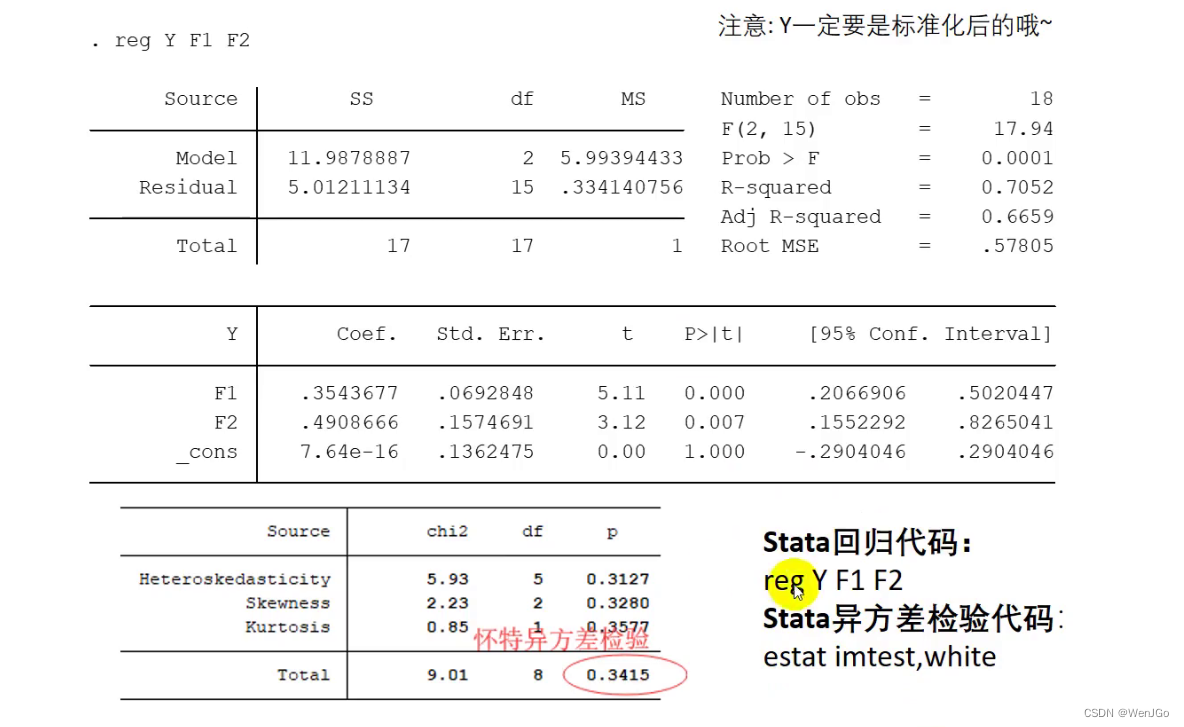
数模学习day06-主成分分析
主成分分析(Principal Component Analysis,PCA)主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说当研究的问题涉及到…...

Windows PowerShell的安全目标——安全警报
Windows PowerShell的安全目标——安全警报 1. 保证Shell安全 自从2006年年底PowerShell发布以来,微软在安全和脚本方面并没有取得很好的名声。毕竟那个时候,**VBScript和Windows Script Host(WSH)**是两个最流行的病毒和恶意软件的载体,…...
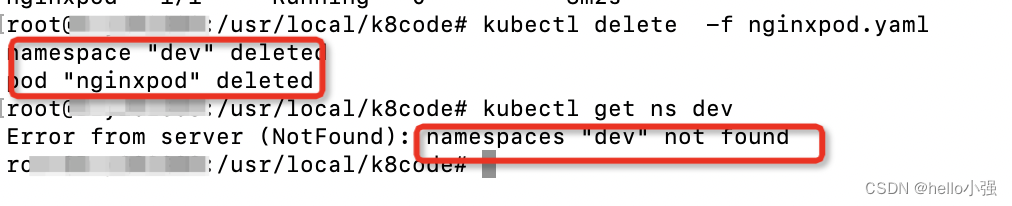
k8s笔记1- 初步认识k8s
k8s简介: kubernetes,俗称k8是,用于自动部署,扩缩和管理容器化应用程序的开源系统,它将组成应用程序的容器,组合成逻辑单元,便于管理和服务发现。 k8s的作用 自动化上线和回滚、存储编排…...
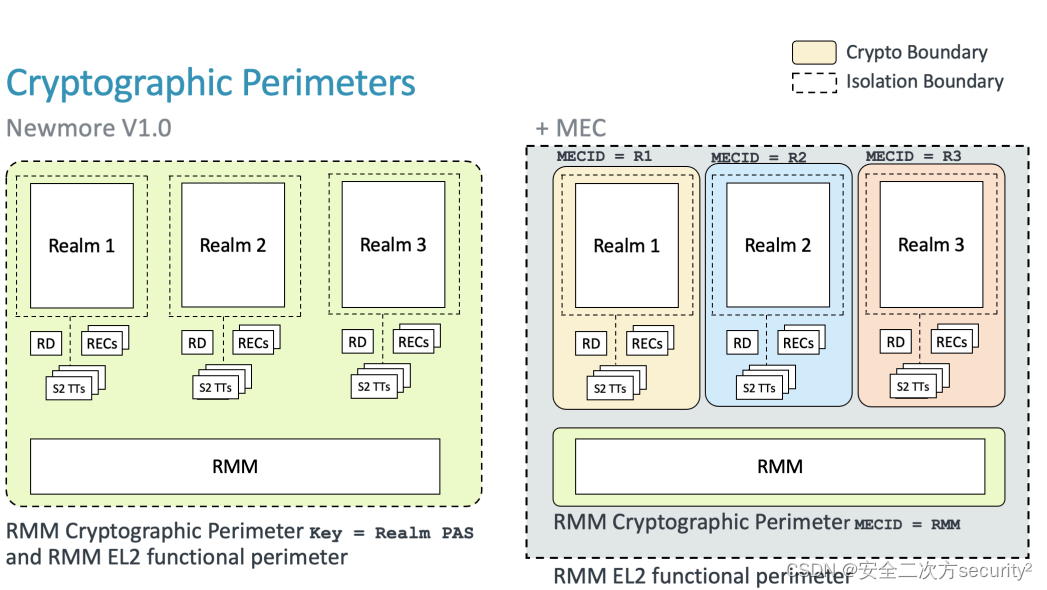
ARM CCA机密计算软件架构之内存加密上下文(MEC)
内存加密上下文(MEC) 内存加密上下文是与内存区域相关联的加密配置,由MMU分配。 MEC是Arm Realm Management Extension(RME)的扩展。RME系统架构要求对Realm、Secure和Root PAS进行加密。用于每个PAS的加密密钥、调整或加密上下文在该PAS内是全局的。例如,对于Realm PA…...

python基于flask实现一个文本问答系统
from flask import Flask, render_template, requestapp Flask(__name__)# 一个简单的问题-答案映射,实际中可以使用更复杂的存储结构(数据库等) qa_pairs {"什么是人工智能?": "人工智能是模拟人类智能的一种机…...

lambda表达式使用和示例
lambda表达式 什么是lambda 学习lamdba有两个结构十分关键,一个是lamdba自己,另一个是函数式接口 lamdba lamdba表达式本质上就是匿名方法,不能独立运行用于实现函数式接口定义的另一个方法,因此lamdba会产生一个匿名类lamdba…...
探索游戏多样性,范围伤害模式)
STM32学习笔记十八:WS2812制作像素游戏屏-飞行射击游戏(8)探索游戏多样性,范围伤害模式
前面我们的攻击手段比较单一,虽然已经分出了 EnemyT1 / EnemyT2 / EnemyT3, 但里面还是基本一样的。这回,我们尝试实现一些新的攻击方法,实现一些新的算法。 1、前面我们小飞机EnemyT1 的攻击方式是垂直向下发射子弹。 那么大飞机…...
C#获取windows系统资源使用情况
1.前言 之前有一篇博客介绍如何获取Linux服务器上的资源使用情况《Java 获取服务器资源(内存、负载、磁盘容量)》,这里介绍如何通过C#获取Window系统的资源使用。 2.获取服务器资源 2.1.内存 [DllImport("kernel32.dll")][retu…...
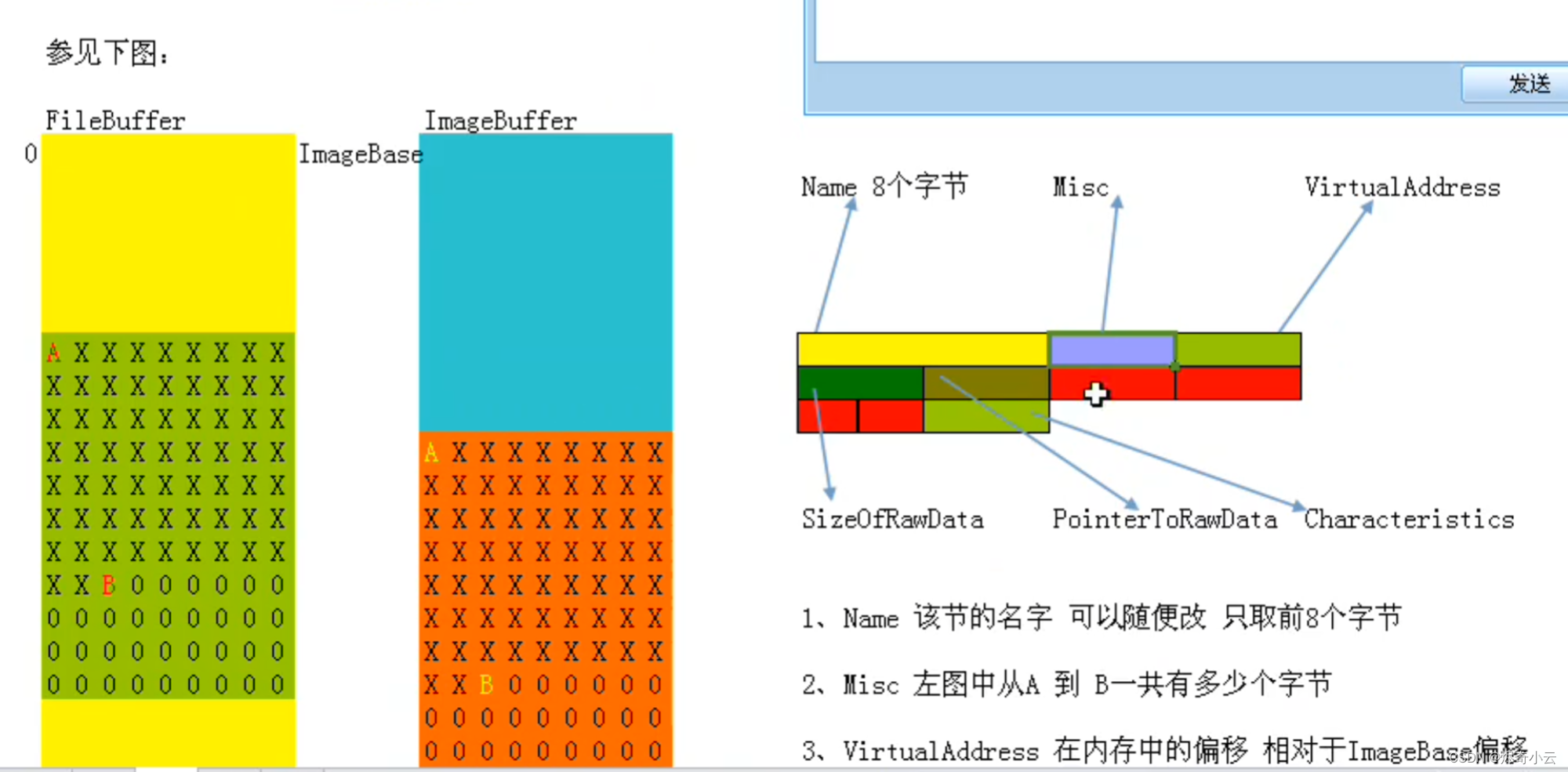
PE解释器之PE文件结构
PE文件是由许许多多的结构体组成的,程序在运行时就会通过这些结构快速定位到PE文件的各种资源,其结构大致如图所示,从上到下依次是Dos头、Nt头、节表、节区和调试信息(可选)。其中Dos头、Nt头和节表在本文中统称为PE文件头(因为SizeOfHeaders…...
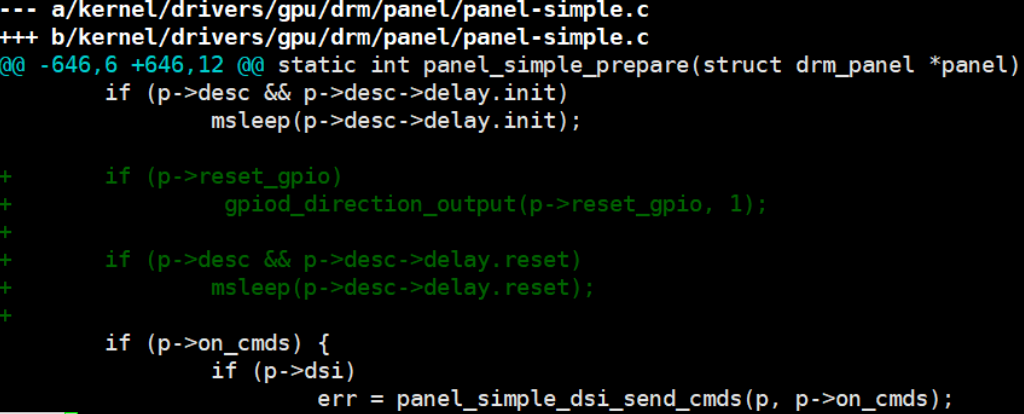
Android—— MIPI屏调试
一、实现步骤 1、在kernel/arch/arm/boot/dts/lcd-box.dtsi文件中打开&dsi0节点,关闭其他显示面板接口(&edp_panel、&lvds_panel) --- a/kernel/arch/arm/boot/dts/lcd-box.dtsib/kernel/arch/arm/boot/dts/lcd-box.dtsi-5,14 …...

BLE协议—协议栈基础
BLE协议—协议栈基础 BLE协议栈基础通用访问配置文件层(Generic Access Profile,GAP)GAP角色设备配置模式和规程安全模式广播和扫描 BLE协议栈基础 蓝牙BLE协议栈包含三部分:主机、主机接口层和控制器。 主机:逻辑链路…...

yolov8知识蒸馏代码详解:支持logit和feature-based蒸馏
文章目录 1. 知识蒸馏理论2. yolov8 蒸馏代码应用2.1 环境配置2.2 训练模型(1) 训练教师模型(2) 训练学生模型baseline(3) 蒸馏训练3. 知识蒸馏代码详解3.1 蒸馏参数设置3.2 蒸馏损失代码讲解3.2.1 Feature based loss3.2.1 Logit loss3.3 获取蒸馏的feature map及channels...
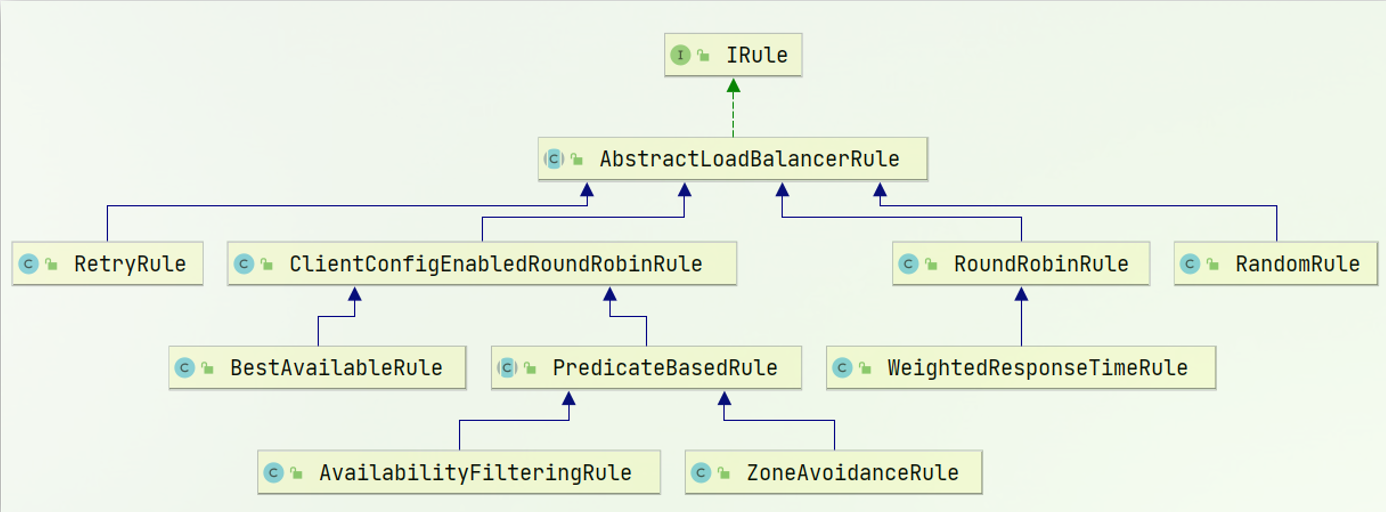
03-微服务-Ribbon负载均衡
Ribbon负载均衡 1.1.负载均衡原理 SpringCloud底层其实是利用了一个名为Ribbon的组件,来实现负载均衡功能的。 那么我们发出的请求明明是http://userservice/user/1,怎么变成了http://localhost:8081的呢? 1.2.源码跟踪 为什么我们只输入…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
