【十一】【C++\动态规划】1218. 最长定差子序列、873. 最长的斐波那契子序列的长度、1027. 最长等差数列,三道题目深度解析
动态规划
动态规划就像是解决问题的一种策略,它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题,并将每个小问题的解保存起来。这样,当我们需要解决原始问题的时候,我们就可以直接利用已经计算好的小问题的解,而不需要重复计算。
动态规划与数学归纳法思想上十分相似。
数学归纳法:
-
基础步骤(base case):首先证明命题在最小的基础情况下成立。通常这是一个较简单的情况,可以直接验证命题是否成立。
-
归纳步骤(inductive step):假设命题在某个情况下成立,然后证明在下一个情况下也成立。这个证明可以通过推理推断出结论或使用一些已知的规律来得到。
通过反复迭代归纳步骤,我们可以推导出命题在所有情况下成立的结论。
动态规划:
-
状态表示:
-
状态转移方程:
-
初始化:
-
填表顺序:
-
返回值:
数学归纳法的基础步骤相当于动态规划中初始化步骤。
数学归纳法的归纳步骤相当于动态规划中推导状态转移方程。
动态规划的思想和数学归纳法思想类似。
在动态规划中,首先得到状态在最小的基础情况下的值,然后通过状态转移方程,得到下一个状态的值,反复迭代,最终得到我们期望的状态下的值。
接下来我们通过三道例题,深入理解动态规划思想,以及实现动态规划的具体步骤。
1218. 最长定差子序列 - 力扣(LeetCode)

题目解析

状态表示
状态表示一般通过经验+题目要求得到,
经验一般指,以某个位置为结尾,或者以某个位置为开始。
我们可以很容易得到这样一个状态表示,定义dp[i]表示以i位置为结尾的最长的等差子序列的长度。
状态转移方程
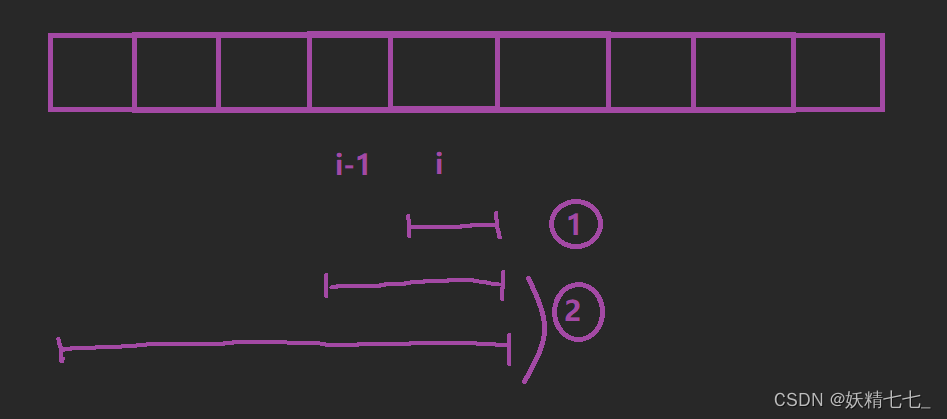
dp[i]表示以i位置为结尾的最长的等差子序列的长度。
我们针对于(以i位置元素为结尾的等差子序列,以及i位置元素)进行分析,想一想dp[i]能不能由其他状态推导得出。
-
如果只考虑i位置一个元素, 等差子序列只有i位置一个元素,长度为1,故dp[i]=1。
-
如果不止考虑i位置一个元素, 那么i位置元素可能跟在前面(0~i-1)中任意满足(arr[i]-arr[j]=difference)的元素后面,(0<=j<=i-1),对于确定的一个j值,此时dp[i]=dp[j]+1,意味着j位置元素和i位置元素构成等差子序列。 由于(0<=j<=i-1) 所以dp[i]=max(dp[i],dp[j]+1),需要在(0~i-1)这些状态中找到最大的值存储在dp[i]中。
将上述情况进行合并和简化,
-
如果第二种情况,至少有一个j满足情况,进行了赋值操作。
-
因为dp[i]的取值需要在自己和前面的值中选取最大的一个,并且是赋值,所以在最开始的赋值中,自己必须有初始值。
-
在自己初始化的前提下,dp[i]一定会被赋值为一个大于1的值,所以就不会取到第一种情况。
-
-
如果第二种情况,没有一个j满足要求,没有进行赋值操作。 那么dp[i]就只能自己构成等差子序列,dp[i]就等于1。
综上所述,我们需要初始化所有位置状态为1,保证dp[i]最开始有初始值,同时状态初始化为1,是最长等差子序列的最低标准,把只有自己一个元素的情况考虑进去了。
状态转移方程为,
for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (arr[i] - arr[j] == difference) {dp[i] = fmax(dp[i], dp[j] + 1);}}}初始化
根据状态转移方程,我们知道,想要推导出i位置的状态,需要用到(0~i-1)位置的状态,所以我们需要初始化第一个位置的状态,即dp[0]=1。
根据在状态转移方程的分析,我们需要将所有位置状态初始化为1,结合起来得到初始化,
初始化为,
for (int i = 0; i < n; i++) {dp[i] = 1;}填表顺序
根据状态转移方程,我们知道想要推导出i位置状态,需要运用到(0~i-1)位置的状态,所以我们需要从左往右填写,保证在推导i位置的状态时,(0~i-1)位置的状态都已经得到。
即,从左往右填写。
返回值
dp[i]表示以i位置为结尾的最长的等差子序列的长度。
结合题目意思,我们需要得到所有等差子序列中长度最长的长度值,所以我们需要遍历dp表,找到长度最长的长度值,然后返回。
代码实现
我们最容易得到的代码:(时间复杂度是O(n^2),但是结果超时了)
int longestSubsequence(int* arr, int arrSize, int difference) {int n = arrSize;int dp[n];for (int i = 0; i < n; i++) {dp[i] = 1;}int ret = 1;for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (arr[i] - arr[j] == difference) {dp[i] = fmax(dp[i], dp[j] + 1);}}ret = fmax(ret, dp[i]);}return ret;
}所以我们必须将优化时间复杂度。
我们进行优化,最外层的循环是一定优化不了的,因为我们必须遍历dp表一遍去填写每一个值,所以我们希望优化内循环,看看能不能降低时间复杂度。
我们内循环的作用是,对于i位置的元素,遍历所有可能构成的等差序列,找到最大长度,然后赋值给dp[i]。
(遍历所有可能构成的等差序列)我们知道一个重要的信息,arr[i] - arr[j] == difference。
也就是我们满足要求的元素值我们是知道的,arr[j],
我们想能不能根据这个元素值直接找到最长的等差序列的长度?
如果可以实现,就可以把内循环的一层遍历优化为O(1)。
通过关键值直接访问,这不就是hash表吗?
如果hash表下标记录元素值,hash值记录最长的等差序列的长度,这样就可以实现优化。
既然hash值存储的是长度即dp,那么我们就做到将(元素,dp)进行绑定。就不需要dp数组了。
hash存储的就是最长长度,相当于代替了dp的作用。
这里我用c++实现,(因为c++更方便一点,c语言hash表下标不能存负数)
class Solution {
public:int longestSubsequence(vector<int>& arr, int difference) {unordered_map<int, int> hash;hash[arr[0]] = 1;int ret = 1;for (int i = 1; i < arr.size(); i++) {hash[arr[i]] = hash[arr[i] - difference] + 1;ret = fmax(ret, hash[arr[i]]);}return ret;}
};873. 最长的斐波那契子序列的长度 - 力扣(LeetCode)

题目解析

状态表示
状态表示一般通过经验+题目要求得到,
经验一般指,以某个位置为结尾,或者以某个位置为开始。
我们可以很容易得到这样一个状态表示,定义dp[i]表示以i位置为结尾的最长的斐波那契子序列的长度。
我们可以尝试推导一下对应的状态转移方程。
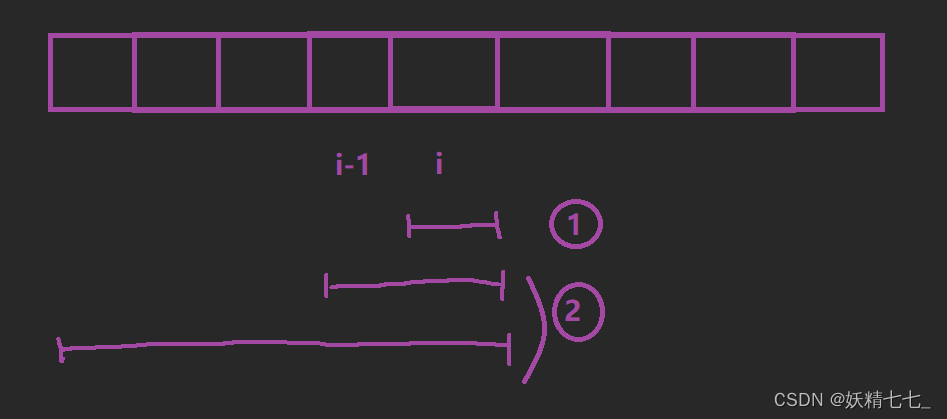
dp[i]表示以i位置为结尾的最长的斐波那契子序列的长度。
我们针对于(以i位置元素为结尾的斐波那契子序列,以及i位置元素)进行分析,想一想dp[i]能不能由其他状态推导得出。
-
如果只考虑i位置一个元素, 因为斐波那契子序列最少要含有三个元素,所以实际上dp[i]应该为0,如果dp[i]为零,没办法区分i位置元素最多和前面0个元素构成斐波那契子序列还是和前面1个元素构成斐波那契子序列,因此我们这里dp[i]存储1,表示只能和前面0个元素构成斐波那契子序列,而只需要判断dp[i]的值是不是小于3就知道这个值的含义。
-
如果不止考虑i位置一个元素, i位置元素可能跟在前面的任意位置元素后面,(0~i-1)定义(0<=j<=i-1),针对j位置元素,如果i位置元素和j位置元素构成斐波那契子序列,那么arr[i]=arr[j]+(前一个元素),但我们不知道以j位置元素结尾的最长子序列前一个元素是不是我们希望的那个元素,所以这个状态表示不足以推导出状态转移方程。
我们可以修正一个状态转移方程,定义dp[i][j]表示以i位置和j位置为结尾的所有子序列中,最长的斐波那契子序列长度。
固定了最后两个位置的斐波那契子序列,就可以推导出前一个位置的元素,即,arr[j]-arr[i]。
以(arr[j]-arr[i])这个元素对应下标位置和i位置结尾的所有子序列中,最长的斐波那契子序列长度是dp[x][i]就可以推导出状态转移方程。
因此状态表示为,定义dp[i][j]表示以i位置和j位置为结尾的所有子序列中,最长的斐波那契子序列长度。
状态转移方程
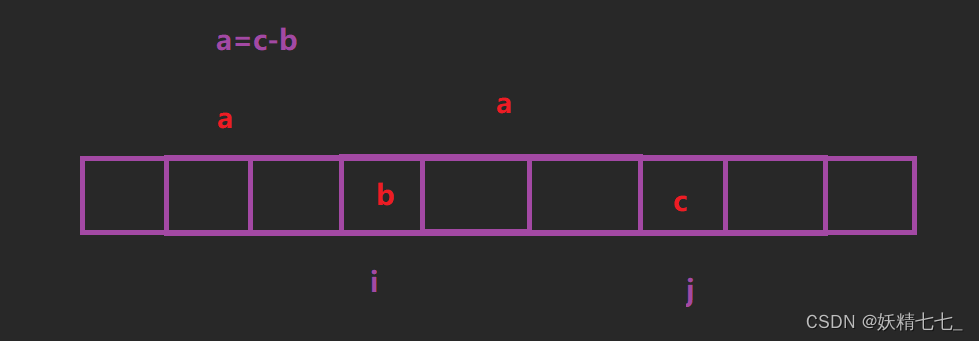
dp[i][j]表示以i位置和j位置为结尾的所有子序列中,最长的斐波那契子序列长度。
我们针对于(以i、j位置元素为结尾的斐波那契子序列)进行分析,想一想dp[i][j]能不能由其他状态推导得出。
假设arr[i]=b,arr[j]=c,那么这个序列前一个元素就是a=c-b。我们根据a的情况进行讨论,
-
a存在,
-
a<b, 假设a的下标为k,此时以i、j位置为结尾的最长斐波那契子序列长度为以k,i位置为结尾的最长斐波那契子序列长度+1。即dp[i][j]=dp[k][i]+1。
-
a>b, 假设a的下标为k,此时k介于i和j之间,所以这种情况不成立,此时dp[i][j]=2。
-
-
a不存在, 此时dp[i][j]=2。
将上述情况进行合并和简化,
如果a存在且a<b,dp[i][j]=dp[k][i]+1,其他情况dp[i][j]=2,所以我们可以把其他情况放到初始化步骤进行解决,全部状态初始化为2即可。这样就只需要考虑一种情况。
我们发现,在状态转移方程中,我们需要确定 a 元素的下标。因此我们可以在 dp 之
前,将所有的「元素+下标」绑定在一起,放到哈希表中。
即,
unordered_map<int, int> hash;for (int i = 0; i < n; i++)hash[arr[i]] = i;这样我们就可以快速通过a元素值找到对应的下标,并且可以快速知道arr数组中是否存在a元素。
状态转移方程为,
for (int j = 2; j < n; j++) // 固定最后一个位置{for (int i = 1; i < j; i++) // 固定倒数第二个位置{int a = arr[j] - arr[i];// 条件成立的情况下更新if (a < arr[i] && hash.count(a))dp[i][j] = dp[hash[a]][i] + 1;}}初始化
根据状态转移方程,我们知道在推导(i,j)位置的状态时,可能要用到(0~i-1)(i)位置的状态,所以我们初始化最基础的最小的解,推导第二个状态((1,2)位置的状态)时,需要初始化(0~1-1)(i)即dp[0][1]=2。
结合在状态转移方程中的分析,所有状态都要初始化为2,故初始化为,
vector<vector<int>> dp(n, vector<int>(n, 2));填表顺序
根据状态转移方程,我们知道在推导(i,j)位置的状态时,可能要用到(0~i-1)(i)位置的状态,所以在填写(i,j)位置的状态时,(k,i)位置的状态必须已经填写好,(0<=k<=i-1)。
如果固定j填写i,我们需要用到的是(k,i),i对应的状态应该已经全部填写,所以j应该从小到大变化。此时i的变化可以从小到大也可以从大到小。
如果固定i填写j,我们需要用到的是(k,i),k对应的状态应该已经全部填写,所以i应该从小到大变化。此时j的变化可以从小到大也可以从大到小。
返回值
dp[i][j]表示以i位置和j位置为结尾的所有子序列中,最长的斐波那契子序列长度。
结合题目意思,我们需要返回最长斐波那契子序列长度,但我们不知道最长的斐波那契子序列以哪两个位置结尾,所以我们需要遍历dp表找到最大值然后返回。
代码实现
class Solution {
public:int lenLongestFibSubseq(vector<int>& arr) {int n = arr.size();// 优化unordered_map<int, int> hash;for (int i = 0; i < n; i++)hash[arr[i]] = i;int ret = 2;vector<vector<int>> dp(n, vector<int>(n, 2));for (int j = 2; j < n; j++) // 固定最后一个位置{for (int i = 1; i < j; i++) // 固定倒数第二个位置{int a = arr[j] - arr[i];// 条件成立的情况下更新if (a < arr[i] && hash.count(a))dp[i][j] = dp[hash[a]][i] + 1;ret = max(ret, dp[i][j]); // 统计表中的最大值}}return ret < 3 ? 0 : ret;}
};1027. 最长等差数列 - 力扣(LeetCode)

题目解析

状态表示
状态表示一般通过经验+题目要求得到,
经验一般指,以某个位置为结尾,或者以某个位置为开始。
我们可以很容易得到这样一个状态表示,定义dp[i]表示以i位置为结尾的最长的等差子序列的长度。
我们可以尝试推导一下对应的状态转移方程。
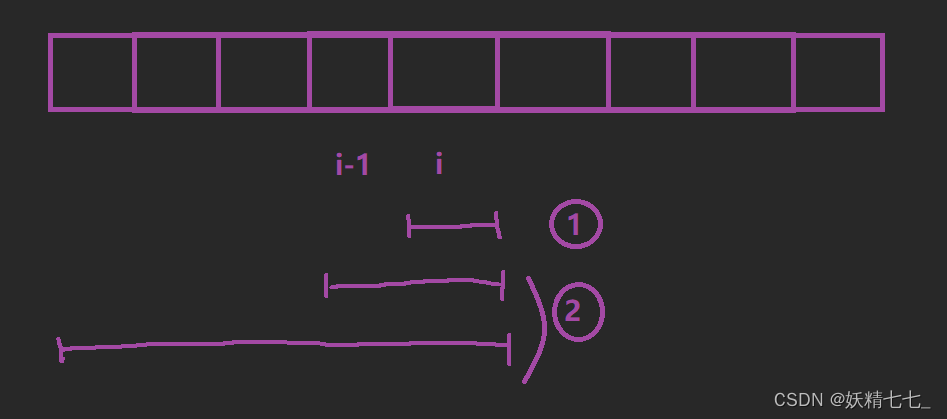
我们针对(以i位置为结尾的等差子序列)进行分析,想一想dp[i]能不能由其他状态推导得出。
-
如果只考虑i位置一个元素, dp[i]=1。
-
如果不止考虑i位置一个元素, i位置元素可以跟在前面任意一个元素后面,定义(0<=j<=i-1)但是我们不知道dp[j]代表的最长等差子序列长度所对应的等差子序列公差是多少,没办法确定是否可以使得(j,i)位置构成的等差子序列和(以j位置结尾的最长等差子序列长度对应的等差子序列)公差相等。所以这个状态表示不足以推导出状态转移方程。
我们可以修正状态表示,定义dp[i][j]表示以(i,j)为结尾的等差子序列最长的长度值。
因为我们只需要根据arr[i]、arr[j]两个元素就知道以(i,j)位置结尾的等差子序列长什么样子,就可以推导出该等差子序列前一个元素值,因为arr[i]-x=arr[j]-arr[i],所以x=2*arr[i]-arr[j]。
这样dp[i][j]=dp[x对应的下标][i]+1。
就可以推导出状态转移方程。
所以状态表示为,
定义dp[i][j]表示以(i,j)为结尾的等差子序列最长的长度值。
状态转移方程
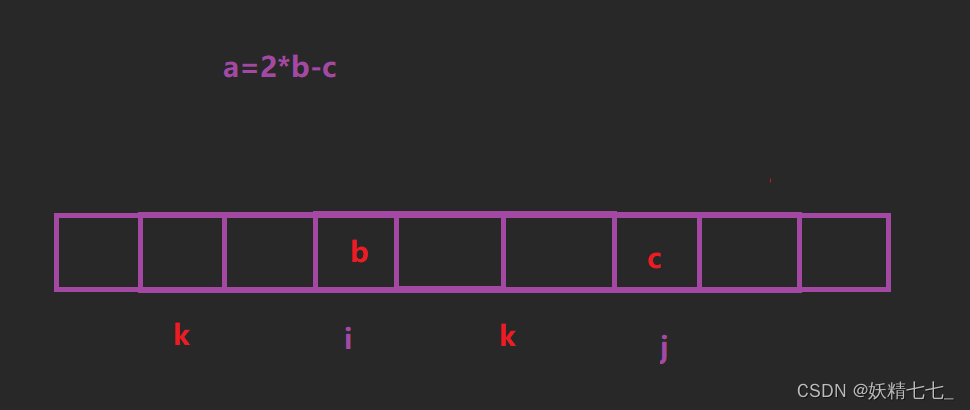
设nums[i] = b,nums[j] = c,那么这个序列的前一个元素就是a = 2 * b - c。我们根据a的情况讨论:(假设a的下标是k)
-
a存在,
-
k<i, 此时我们需要以(k,i)位置结尾的最长等差子序列再加上j位置元素,就是以(i,j)为结尾的最长等差子序列长度,即dp[i][j]=dp[k][i]+1。
-
k>i, 此时不满足等差子序列的定义,所以不考虑这种序列,即dp[i][j]=2。
-
-
a不存在, 此时dp[i][j]=2。
将上述情况进行合并和简化,如果a存在且k<i,dp[i][j]=dp[k][i]+1。其他情况dp[i][j]=2,所以我们可以将dp表初始化为2,只用考虑a存在且k<i的情况。
我们发现,在状态转移方程中,我们需要确定 a 元素的下标。因此我们可以在 dp 之前,将所有的「元素+下标」绑定在一起,放到哈希表中。
这样我们就可以快速通过a元素值找到对应的下标,并且可以快速知道arr数组中是否存在a元素。
故,状态转移方程为
for (int i = 1; i < n; i++) // 固定倒数第一个数{for (int j = i + 1; j < n; j++) // 枚举倒数第二个数{int a = 2 * nums[i] - nums[j];if (hash.count(a)&&hash[a]<i)dp[i][j] = dp[hash[a]][i] + 1;}}初始化
根据状态转移方程,我们知道推导(i,j)位置状态时,可能用到(k,i)位置状态,而(0<=k<=i-1),所以我们初始化最基础的最小的解,推导第二个状态((1,2)位置的状态)时,需要初始化(0~1-1)(i)即dp[0][1]=2。
结合在状态转移方程中的分析,所有状态都要初始化为2,故初始化为,
vector<vector<int>> dp(n, vector<int>(n, 2)); // 创建 dp 表 + 初始化填表顺序
根据状态转移方程,我们知道推导(i,j)位置状态时,可能用到(k,i)位置状态,(0<=k<=i-1),所以此时(k,i)位置的状态应该已经得到。
如果固定j填写i,我们需要用到的是(k,i),i对应的状态应该已经全部填写,所以j应该从小到大变化。此时i的变化可以从小到大也可以从大到小。
如果固定i填写j,我们需要用到的是(k,i),k对应的状态应该已经全部填写,所以i应该从小到大变化。此时j的变化可以从小到大也可以从大到小。
返回值
dp[i][j]表示以(i,j)为结尾的等差子序列最长的长度值。
结合题目意思,我们需要返回等差子序列最长的长度值,但是我们不知道最长的等差子序列是以哪两个位置结尾,所以我们需要遍历dp表找到最大值进行返回。
代码实现
class Solution {
public:int longestArithSeqLength(vector<int>& nums) {unordered_map<int, int> hash;hash[nums[0]] = 0;int n = nums.size();vector<vector<int>> dp(n, vector<int>(n, 2)); // 创建 dp 表 + 初始化int ret = 2;for (int i = 1; i < n; i++) // 固定倒数第一个数{for (int j = i + 1; j < n; j++) // 枚举倒数第二个数{int a = 2 * nums[i] - nums[j];if (hash.count(a))dp[i][j] = dp[hash[a]][i] + 1;ret = max(ret, dp[i][j]);}hash[nums[i]] = i;}return ret;}
};结尾
今天我们学习了动态规划的思想,动态规划思想和数学归纳法思想有一些类似,动态规划在模拟数学归纳法的过程,已知一个最简单的基础解,通过得到前项与后项的推导关系,由这个最简单的基础解,我们可以一步一步推导出我们希望得到的那个解,把我们得到的解依次存放在dp数组中,dp数组中对应的状态,就像是数列里面的每一项。最后感谢您阅读我的文章,对于动态规划系列,我会一直更新,如果您觉得内容有帮助,可以点赞加关注,以快速阅读最新文章。
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
相关文章:

【十一】【C++\动态规划】1218. 最长定差子序列、873. 最长的斐波那契子序列的长度、1027. 最长等差数列,三道题目深度解析
动态规划 动态规划就像是解决问题的一种策略,它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题,并将每个小问题的解保存起来。这样,当我们需要解决原始问题的时候,我们就可以直接利…...

主板部件
▶1.主要部件 主板是计算机的重要部件,主板由集成电路芯片、电子元器件、电路系统、各种总线插座和接口组成,目前主板标准为ATX。主板的主要功能是传输各种电子信号,部分芯片负责初步处理一些外围数据。不同类型的CPU,需要不同主板与之匹配。…...

2023年度学习总结
想想大一刚开始在CSDN写作,这一坚持,就是我在CSDN的第九个年头,这也是在CSDN最有里程碑的一年,这一年我被评为CSDN的博客专家啦!先是被评为Unity开发领域新星创作者,写的关于一部分Unity开发的心得获得大家…...

服务器感染了.kann勒索病毒,如何确保数据文件完整恢复?
导言: 勒索病毒成为当前网络安全领域的一大威胁。.kann勒索病毒是其中的一种变种,对用户的数据造成了极大的威胁。本文91数据恢复将介绍.kann勒索病毒的特征、应对策略以及预防措施,以帮助用户更好地保护个人和组织的数据安全。当面对被勒索…...

使用results.csv文件数据绘制mAP对比图
yolov5每次train完成(如果没有中途退出)都会在run目录下生成expX目录(X代表生成结果次数 第一次训练完成生成exp0 第二次生成exp1…以此类推)。expX目录下会保存训练生成的weights以及result.txt文件,其中weights是训练…...

【算法刷题】## 算法题目第1讲:双指针处理数组题目 带视频讲解
算法题目第一讲:双指针处理数组题目 解决力扣: [344. 反转字符串][167. 两数之和 II - 输入有序数组][26. 删除有序数组中的重复项][27. 移除元素][283. 移动零][5. 最长回文子串] 配合b站视频讲解食用更佳:https://www.bilibili.com/video/BV1vW4y1P…...
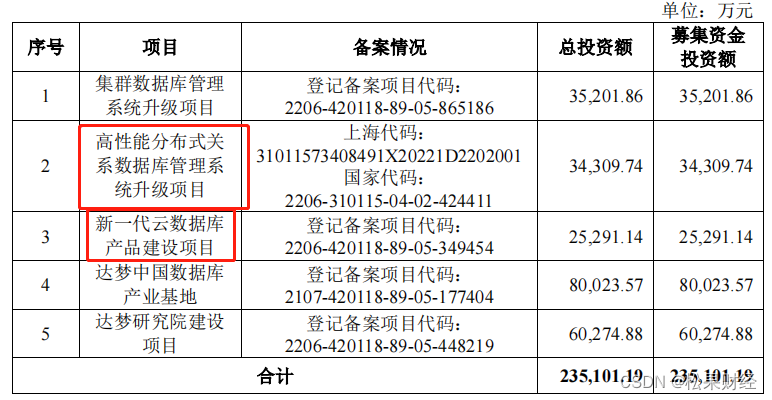
达梦数据:数字化时代,国产数据库第一股终于到来?
又是新的一年开始。回首一年前的此时,在大家千呼万唤地期待中,数据基础制度体系的纲领性文件正式发布。 时隔一年之后,数据资源入表如约而至。2024年1月1日《企业数据资源相关会计处理暂行规定》正式施行,各行各业海量数据巨大的…...

selenium4.0中常见操作方式50条
前阵子升级了py3.9,一些常年陪伴的库也都做了升级,不少命令也更新了,适度更新一下记忆。 1. 打开浏览器:driver webdriver.Chrome() 2. 访问网址:driver.get("Example Domain") 3. 获取当前网址ÿ…...

如何解决使用融云音视频时由于库冲突导致编译不通过的问题
音视频库里面使用了一些第三方库,比如 openssl,libopencore-amrnb 等第三方库,如果集成的过程中遇到冲突可以尝试这样修改: 1、在 Build Settings 中 Other Linker Flags 中把 -all_load 去掉; 2、如果遇到 openssl 库…...
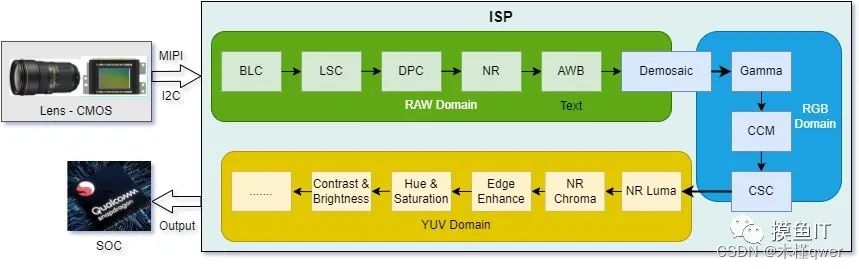
ISP 基础知识积累
Amber:现有工作必要的技术补充,认识需要不断深入,这个文档后续还会增加内容进行完善。 镜头成像资料 ——干货满满,看懂了这四篇文章,下面的问题基本都能解答 看完思考 1、ISP 是什么,有什么作用ÿ…...

Android Studio新手实战——深入学习Activity组件
目录 前言 一、Activity简介 二、任务栈相关概念 三、常用Flag 四、结束当前Activity 五、Intent跳转Activity 六、更多资源 前言 Android是目前全球最流行的移动操作系统之一,而Activity作为Android应用程序的四大组件之一,是Android应用程序的核…...

[足式机器人]Part2 Dr. CAN学习笔记-自动控制原理Ch1-10奈奎斯特稳定性判据-Nyquist Stability Criterion
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-自动控制原理Ch1-10奈奎斯特稳定性判据-Nyquist Stability Criterion Cauchy’s Argument Priciple 柯西幅角原理 结论: s s s平面内顺时针画一条闭合曲线 A A A, B B B曲…...

企业培训系统开发:构建灵活高效的学习平台
企业培训系统的开发在当今数字化时代是至关重要的。本文将介绍一些关键技术和代码示例,以帮助您构建一个灵活、高效的企业培训系统。 1. 技术选型 在开始企业培训系统的开发之前,首先需要选择合适的技术栈。以下是一个基本的技术选型示例:…...

2023秋电子科大信软 程算I 机考真题
基本情况 对应课程:程序设计与算法基础I 考试时间:2小时 题型:函数题编程题 函数题只需要完成期中一些(个)函数即可 编程题需要自己手动写main函数 提示:本次考试为全年级机考,分上下午场&am…...
Hive用户自定义函数之UDF开发
在进行大数据分析或者开发的时候,难免用到Hive进行数据查询分析,Hive内置很多函数,但是会有一部分需求需要自己开发,这个时候就需要自定义函数了,Hive的自定义函数开发非常方便,今天首先讲一下UDF的入门开发…...
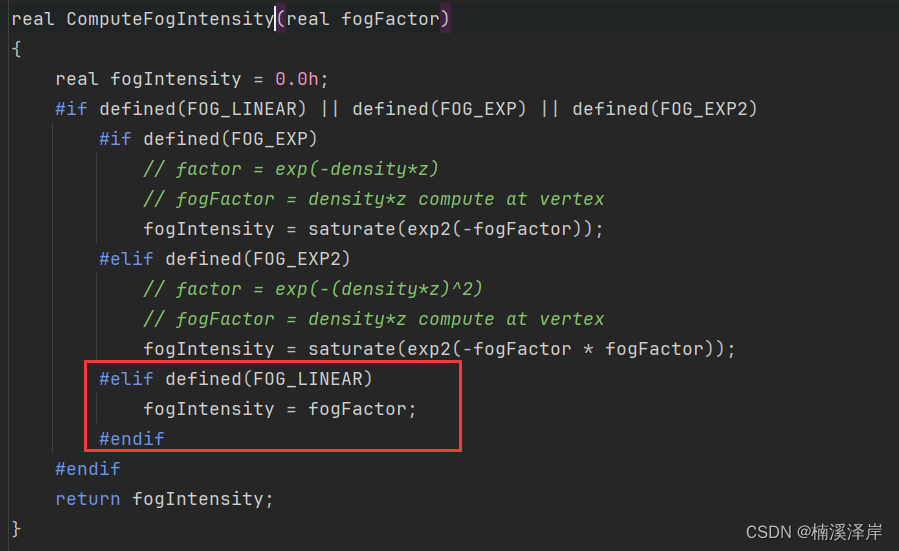
Unity中URP下的线性雾
文章目录 前言一、线性雾 雾效因子二、MixFog1、ComputeFogIntensity 雾效强度计算2、雾效颜色混合 lerp(fogColor, fragColor, fogIntensity); 前言 在之前的文章中,我们实现了URP下的雾效支持。 Unity中URP下的添加雾效支持 在上一篇文章中,我们解析了 URP 下统…...
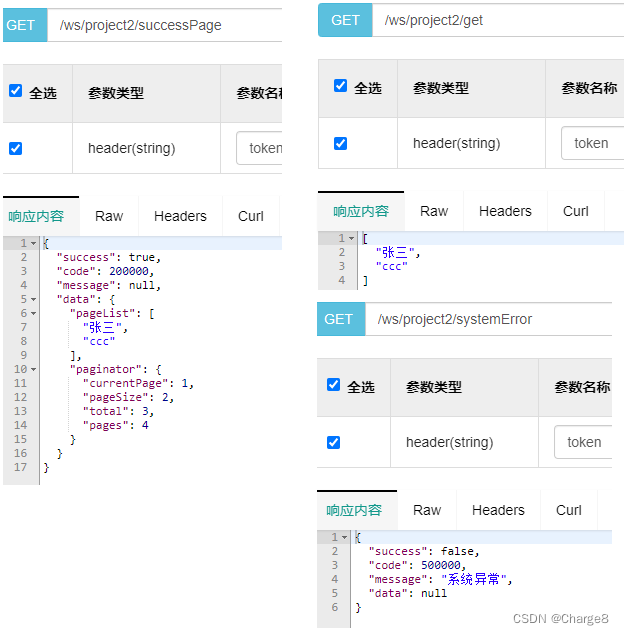
SpringBoot全局Controller返回值格式统一处理
一、Controller返回值格式统一 1、WebResult类 在 Controller对外提供服务的时候,我们都需要统一返回值格式。一般定义一个 WebResult类。 统一返回值(WebResult类)格式如下: {"success": true,"code": 2…...
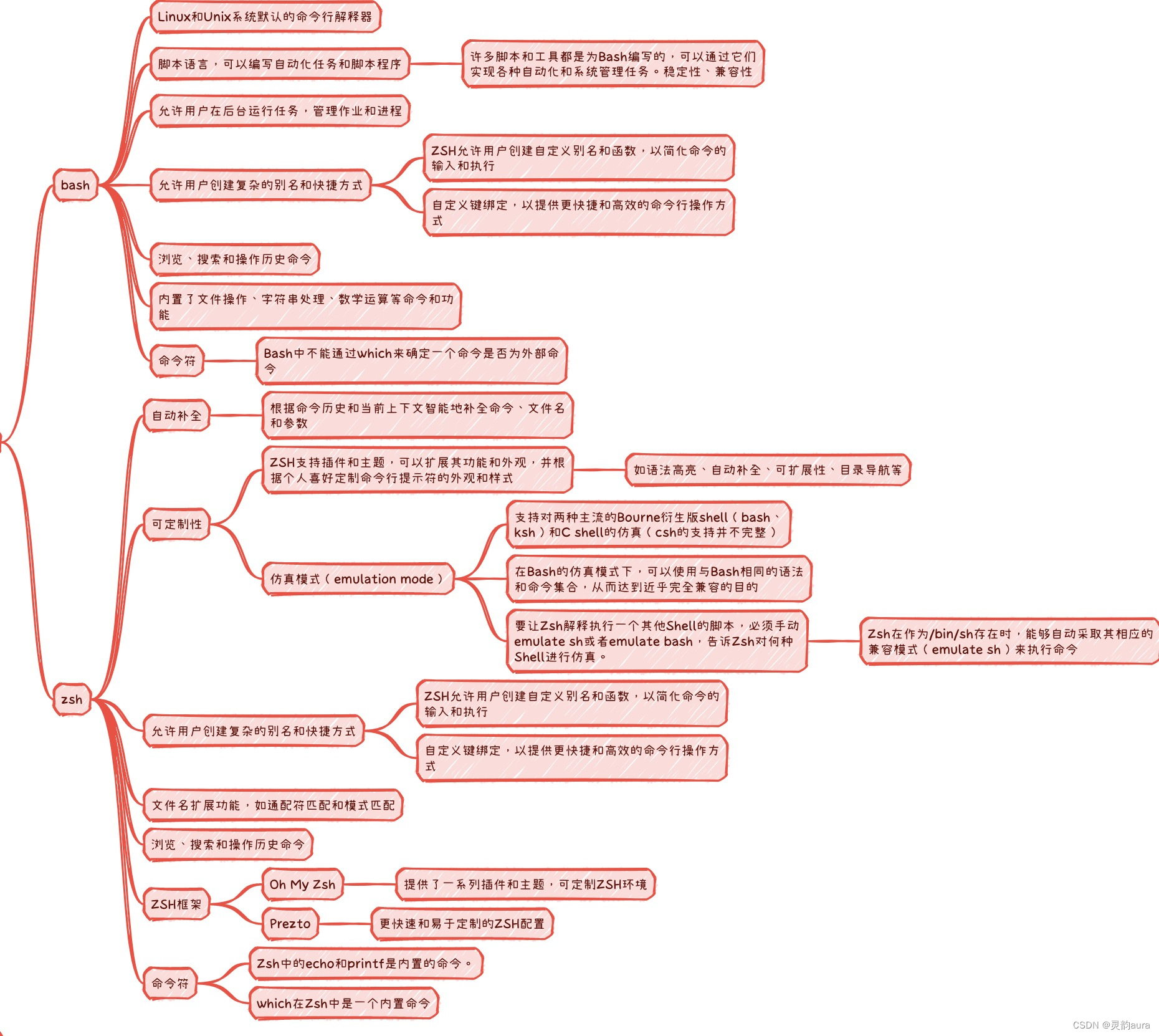
程序媛的mac修炼手册-- 终端shell的驾驭 zsh vs bash
进入终端(Terminal)为新下载的应用配置环境,是Mac生产力up up的关键一步,更是编程小白装大神的第一步。Fake it till you make it , 硅谷大神标准路径~ shell的基本原理 为应用配置环境,相当于在应用和操作系统间架桥。由此&…...
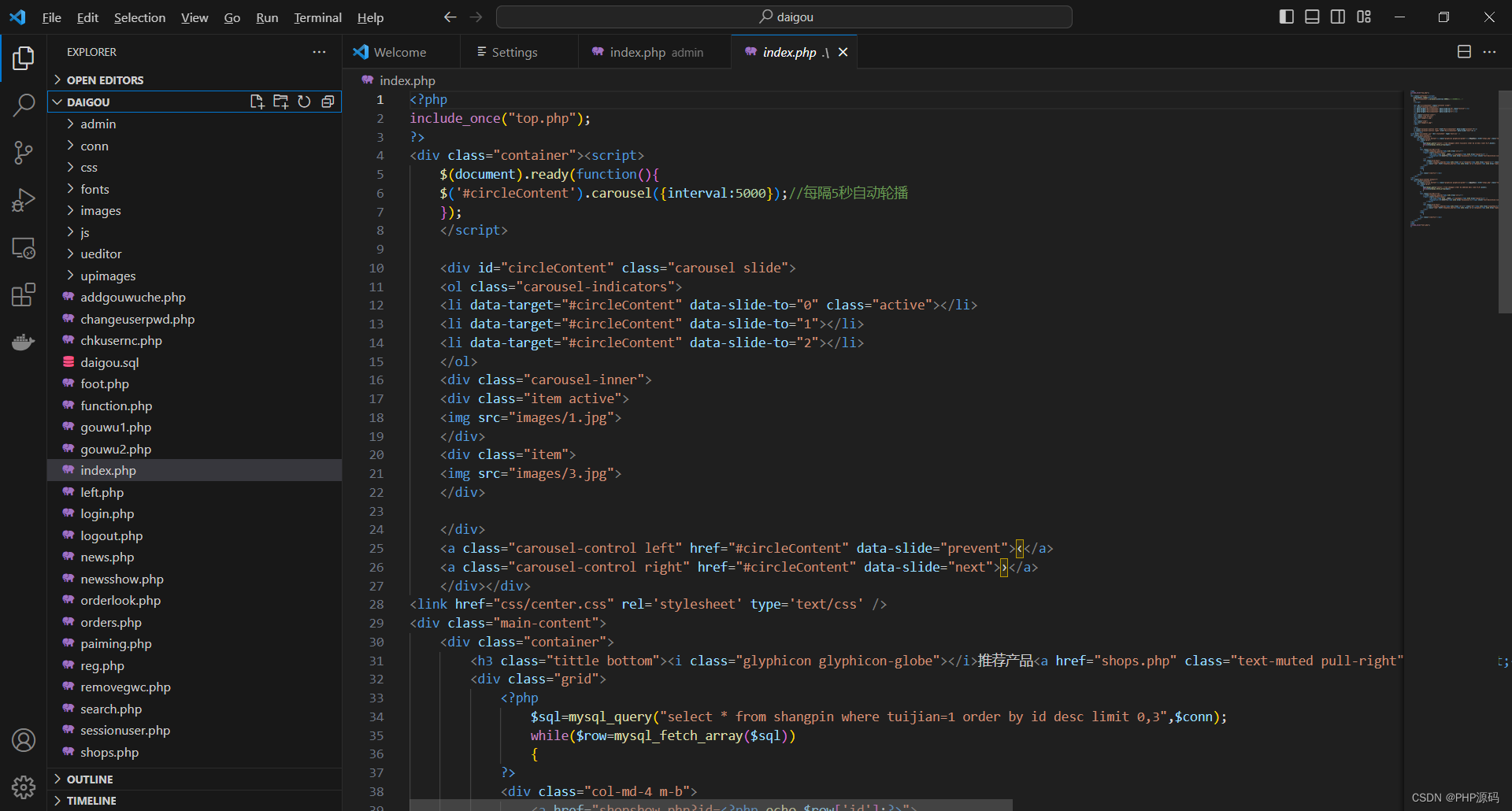
基于PHP的校园代购商城系统
有需要请加文章底部Q哦 可远程调试 基于PHP的校园代购商城系统 一 介绍 此校园代购商城系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。(附带参考设计文档) 技术栈:phpmysqlbootstrapphpstudyvscode 二 功能 …...

感知与认知的碰撞,大模型时代的智能文档处理范式
目录 0 写在前面1 GPT4-V:拓宽文档认知边界2 大语言模型的文档感知缺陷3 大一统文档图像处理范式3.1 像素级OCR任务3.2 OCR大一统模型3.3 长文档理解与应用 4 总结抽奖福利 0 写在前面 由中国图象图形学学会青年工作委员会发起的第十九届中国图象图形学学会青年科学…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
