数字信号处理期末复习——计算大题(一)
个人名片:
🦁作者简介:一名喜欢分享和记录学习的在校大学生
🐯个人主页:妄北y🐧个人QQ:2061314755
🐻个人邮箱:2061314755@qq.com
🦉个人WeChat:Vir2021GKBS
🐼本文由妄北y原创,首发CSDN🎊🎊🎊
🐨座右铭:大多数人想要改造这个世界,但却罕有人想改造自己。
专栏导航:
妄北y系列专栏导航:
C/C++的基础算法:C/C++是一种常用的编程语言,可以用于实现各种算法,这里我们对一些基础算法进行了详细的介绍与分享。🎇🎇🎇
C/C++刷题库:分享一些关于编程的练习基础题,也会后续加入一系列的算法题,分享自己的解题思路和方法。🥰🥰🥰
计算机网络:对计算机网络的基础知识框架有一个简单的学习与认识,对计算机网络中常见的题型进行一个总结与归纳。🍾🍾🍾
QT基础入门学习:对QT的基础图形化页面设计进行了一个简单的学习与认识,利用QT的基础知识进行了翻金币小游戏的制作🤹🤹🤹
Linux基础编程:初步认识什么是Linux,为什么学Linux,安装环境,进行基础命令的学习,入门级的shell编程。🍻🍻🍻
Linux的系统编程+网络编程:IO编程、进程、线程、进程间通讯(包括管道、信号、信号量、共享内存等)网络编程主要就是socket,poll,epoll,以及对TCP/IP的理解,同时要学会高并发式服务器的编写。🙌🙌🙌
Linux应用开发基础开发:分享Linux的基本概念、命令行操作、文件系统、用户和权限管理等,网络编程相关知识,TCP/IP 协议、套接字(Socket)编程等,可以实现网络通信功能。💐💐💐
Linux项目开发:Linux基础知识的实践,做项目是最锻炼能力的一个学习方法,这里我们会学习到一些简单基础的项目开发与应用,而且都是毕业设计级别的哦。🤸🤸🤸
非常期待和您一起在这个小小的互联网世界里共同探索、学习和成长。💝💝💝 ✨✨ 欢迎订阅本专栏 ✨✨

文章介绍:
🎉本篇文章对数字信号处理学习的相关知识进行分享!🥳🥳🥳
😄临近期末考试的我发奋一周学会数字信号处理hhh,开玩笑的哈,大家平时一定要好好学习,在最后的期末周对本学期的知识点和经典题型进行一个归纳总结,相信大家一定可以取得一个优异且满意的成绩。👍
如果您觉得文章不错,期待你的一键三连哦,你的鼓励是我创作动力的源泉,让我们一起加油,一起奔跑,让我们顶峰相见!!!💪💪💪
🎁感谢大家点赞👍收藏⭐评论✍️
目录:
题型一:
题目内容:
题解:
最终结果:
类似题型:
题型二:
题目内容:
题解:
最终结果:
类似题型:
题型三:
题目要求:
题解:
最终结果:
类似题型:
题型四:
题目要求:
题解:
最终结果:
类似题型:
题型五:
题目要求:
题解:
最终结果:
类似题型:
题型六:
题目要求:
题解:
最终结果:
类似题型:
题型一:
题目内容:

题解:
什么是线性,非线性:
线性系统:满足齐次性和叠加性,如果某一个输入有几个信号加权,那么输出也是这组信号中每一个信号对应的响应的加权。
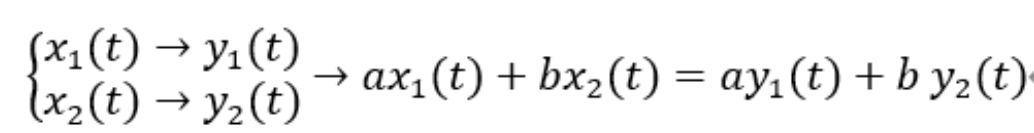
若系统函数中有绝对值、高次项、常数项、非线性运算(求导积分为线性运算),则为非线性。若存在嵌套函数,从外往内依次判断。
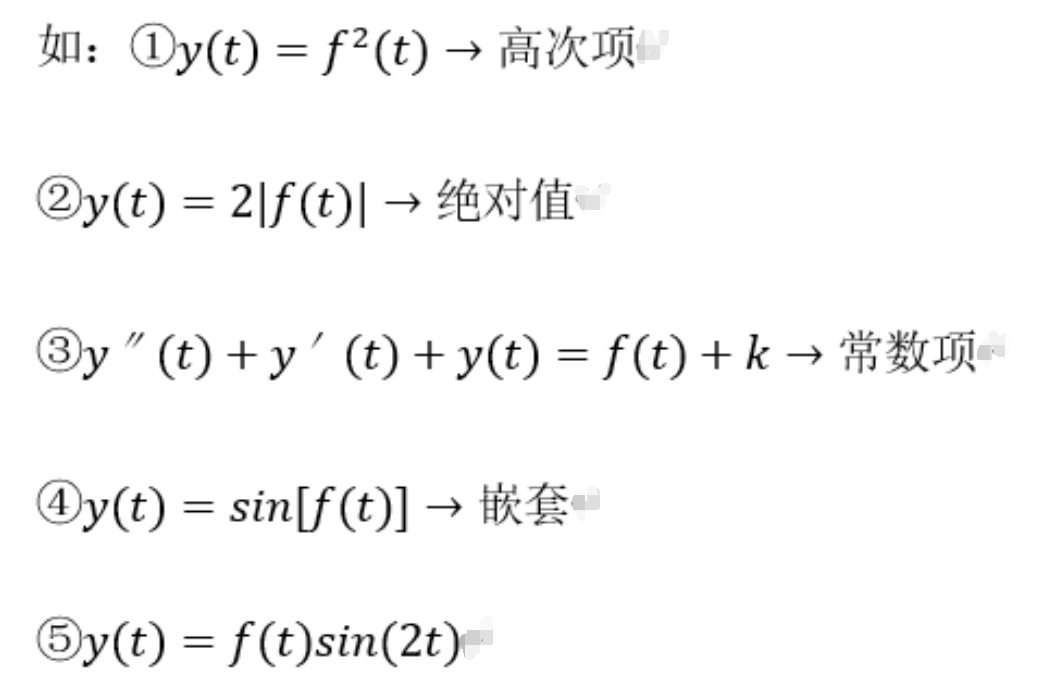
对于本题题解:
![]()
![]() 等于
等于![]()
因此系统为线性系统
什么是时变,时不变:
时不变系统:若系统对输入信号的运算关系不随时间而发生变化,简单说来就是,若输入信号有一个时移,输出信号也随之有一个时移,则为时不变系统。
输入信号f(t)有变系数或f(t)含有反转运算、伸缩尺度变换则时变。

对于本题题解:
![]()
![]() 不等于
不等于![]()
什么是因果,非因果:
因果:输出不超前与输入即可。输出只与当前和过去的输入有关,与将来的输入无关。
判断因果性的时候,以下三点需要着重注意:
(1)对于常系数微分方程,若系统在t<0时,无激励x(t)= 0,且 t=0时刻起始状态为0,则该系统具有因果性。
(2)
(3)y(t)= x(-t),当t>0时为因果,当t<0时为非因果,整体系统为非因果。
y(t)= x(t)cos(t + 1),其输入仅为x(t),cos(t+1)只是与时间有关的函数而已,并非输入。·系统因果。
对于本题题解:
系统n时刻的输出和n时刻以后的输入序列无关
因此系统为因果系统
如果系统的输入是有界的,系统产生的输出不一定有界,因此该系统是非稳定系统。
最终结果:
(1)等于 (2)线性 (3)不等于 (4)时变 (5)无关(6)因果(7)不一定(8)非稳定
类似题型:

(1)等于(2)线性(3)不等于(4)时变(5)有关(6)非因果(7)一定(8)稳定

(1)等于(2)线性(3)不等于(4)时变(5)无关(6)因果(7)不一定(8)非稳定
题型二:
题目内容:

题解:


最终结果:
1.表示系统的输出y(n)与输入x(n)之间关系的差分方程:y(n)-3/4y (n-1)+1/8y (n-2)=x(n)+1/3x (n-1)
2.系统函数的收敛域为|z|>1/2,零点有2个,分别是-1/3,0,极点有2个,分别是1/4,1/2。
3.因为是因果系统,所以系统是稳定的。
类似题型:

y(n)-ay(n-1)=ax (n)-x(n-1) lzl>lal 1 1/a 1 a lal<1
 y(n)-5/2y(n-1)+y(n-2)=-3/2x (n-1) 1/2<|z|<2 1 0 2 1/2 2 非因果
y(n)-5/2y(n-1)+y(n-2)=-3/2x (n-1) 1/2<|z|<2 1 0 2 1/2 2 非因果
题型三:
题目要求:

题解:

1.第一行是[4,0,0,0,0,1,2,3],称为的循环倒相序列。
2.第一行以后的各行均是前一行向右循环移1位形成的。
3.矩阵的各主对角线上的序列值均相等,h(n)的长度为4,需要在h(n)末尾补4个零。最后可计算出
最终结果:

类似题型:

4, 0, 0 , 1 , 2 ,3,循环倒相,右,4,2,5,7 , 9 ,10 , 6 ,3

1, 0, 0,0, 2,2,循环倒相,右,2,4,1, 4,6,4,0,0
题型四:
题目要求:

题解:

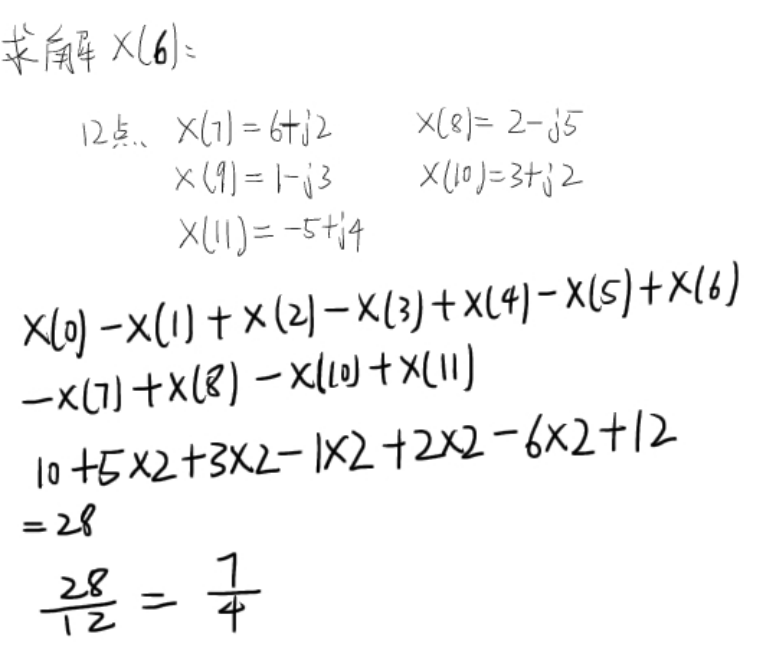

最终结果:

类似题型:

2 , -1 , 6 , 4-3j , 17.25

2 , 2 , 10 , 3+j2 , 35
题型五:
题目要求:

题解:

最终结果:
X(0) = 10 、X(1) = 2 - 2j 、X(2) = 2 、X(3) = 2 + 2j
类似题型:
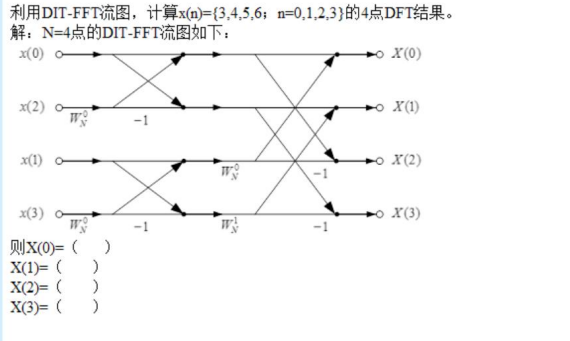
18 , -2+2j , -2, -2-2j
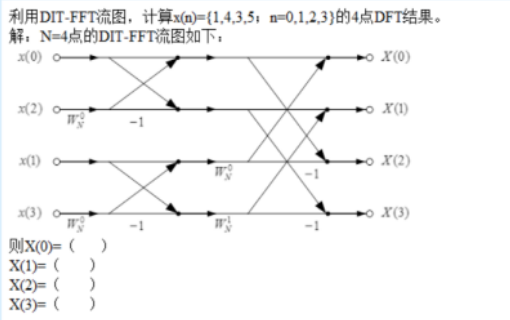
13 ,-2+j ,-5 , -2-j
题型六:
题目要求:

题解:

最终结果:
(1): 1 , (2): -1 , (3): -1 , (4): -5 , (5): 2 , (6): 12 , (7): 8 , (8): 0 , (9): 4 , (10): 8
类似题型:

2/3 , -2/3 , -1 , -4 , 2 , 18 , 0 , -2 , 2 , 4

3 ,-3 ,-1 , -2 , 2, 30 , -28 , 6 , 3 , 6
大佬觉得有用的话点个赞 👍🏻 呗。
❤️❤️❤️本人水平有限,如有纰漏,欢迎各位大佬评论批评指正!😄😄😄💘💘💘如果觉得这篇文对你有帮助的话,也请给个点赞、收藏下吧,非常感谢!👍 👍 👍
🔥🔥🔥任务在无形中完成,价值在无形中升华,让我们一起加油吧!🌙🌙🌙

相关文章:

数字信号处理期末复习——计算大题(一)
个人名片: 🦁作者简介:一名喜欢分享和记录学习的在校大学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:V…...

matlab数值计算函数--ode45
当难以求得微分方程的解析解时,可以求其数值解,Matlab中求微分方程数值解的函数有七个:ode45,ode23,ode113,ode15s,ode23s,ode23t,ode23tb。本文讲解ode45,其…...
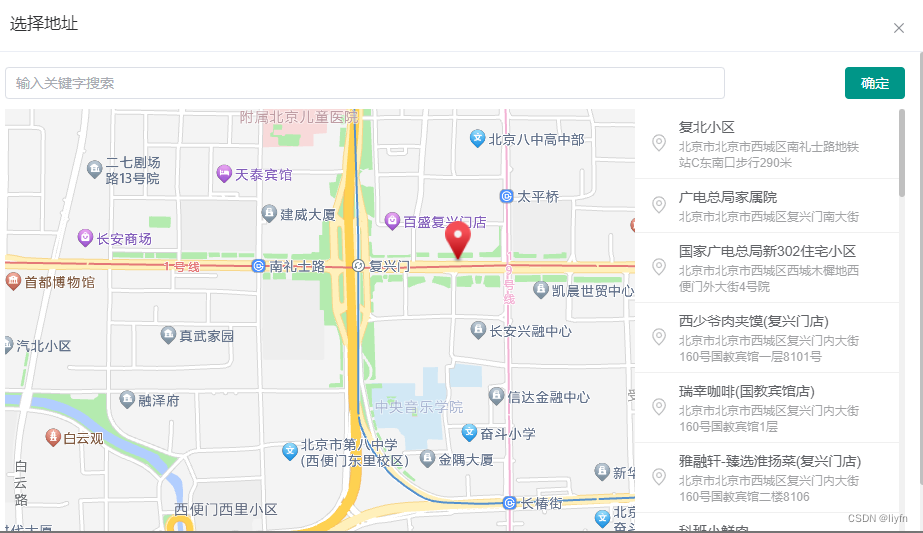
Vue3地图选点组件
Vue3地图选点组件 <template><div style"width: 100%; height: 500px"><div class"search-container"><el-autocompletev-model"suggestionKeyWord"class"search-container__input"clearable:fetch-suggestion…...

JS之注册事件兼容性解决方案
本章介绍注册事件兼容性的解决方案 废话不多说,直接上代码: function addEventListener(element, eventName, fn) {//判断当前浏览器是否支持 addEventListener 方法if (element.addEventListener) {element.addEventListener(eventName, fn); // 第三个…...

C#中使用as关键字将对象转换为指定类型
目录 一、定义 二、示例 三、生成 使用as关键字可以将对象转换为指定类型,与is关键字不同,is关键字用于检查对象是否与给定类型兼容,如果兼容则返回true,如果不兼容则返回false。而as关键字会直接进行类型转换,如果…...

【Spring实战】21 Spring Data REST 常用功能详细介绍
文章目录 1. 资源导出(Resource Exporting)2. 查询方法(Query Methods)3. 分页和排序(Pagination and Sorting)4. 关联关系(Associations)5. 事件(Events)6. …...

05-微服务-RabbitMQ-概述
RabbitMQ 1.初识MQ 1.1.同步和异步通讯 微服务间通讯有同步和异步两种方式: 同步通讯:就像打电话,需要实时响应。 异步通讯:就像发邮件,不需要马上回复。 两种方式各有优劣,打电话可以立即得到响应&am…...

jmeter参数化的三种方式
1.用户定义变量 使用变量: ${变量名} 这个变量是全局变量,也就是在下面子节点中都可以使用; 使用场景:两个账号分别有不同的权限,A经办,B审核。等。。。 2.CSV数据文件设置 3.函数...

java基础之Java8新特性-Lambda
目录 什么是Lambda表达式 Lambda表达式规范 基本语法 参数列表 函数体 注意事项 如何定义函数接口 1.保证接口中只能有一个抽象方法 2.使用FunctionalInterface注解标记该接口为函数接口 使用Lambda调用无参函数 使用Lambda调用有参函数 使用Lambda的精简写法 使用…...

入门使用mybatis-plus
第一步:pom文件带入依赖 <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.5.1</version> </dependency> 第二步:创建实体对象 TableName(&…...
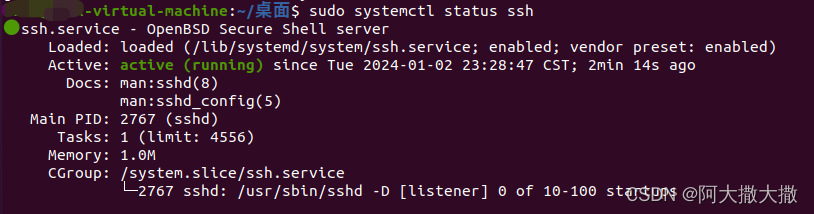
ubuntu安装和配置ssh教程
一、前言 ssh服务类似于windows的远程桌面服务,可以实现对linux系统的远程管理,ssh默认端口为22端口。后面博主进行操作以ubuntu2020操作系统为例进行操作。 二、安装ssh服务 Ubuntu 2020 默认不安装 SSH 服务。它只安装了 SSH 客户端,可以用于连接到其他计算机上的 SSH 服…...

每天刷两道题——第六天
1.1字母异位词分组 给你一个字符串数组,将字母异位词组合在一起。可以按任意顺序返回结果列表。字母异位词指的是由重新排列源单词的所有字母得到的一个新单词。 输入: strs [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”] 输出: [[“bat”],[“nat”,…...

时间序列平稳性相关检验方法
理解平稳性 一般来说,平稳时间序列是指随着时间的推移具有相当稳定的统计特性的时间序列,特别是在均值和方差方面。平稳性可能是一个比较模糊的概念,将序列排除为不平稳可能比说序列是平稳的更容易。通常不平稳序列有几个特征: …...

<leetcode修炼>双指针训练-移动零
题目: 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。 请注意 ,必须在不复制数组的情况下原地对数组进行操作。 方法1: 快慢指针 快指针负责遍历数组中所有元素,慢指针负责记录不为0的…...
Python初探:从零开始的编程奇妙之旅
一、Python是什么 Python是一门多用途的高级编程语言,以其简洁、易读的语法而脱颖而出。在深度学习领域,Python扮演着至关重要的角色。其丰富的科学计算库(如NumPy、Pandas、Matplotlib)和强大的深度学习框架(如Tenso…...
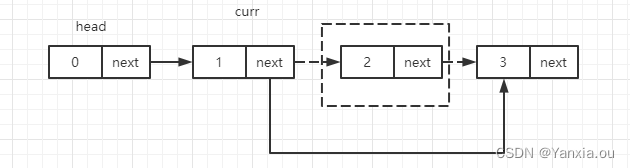
算法与数据结构之链表<一>(Java)
目录 1、链表的定义 2、链表的特点 3、为何要使用链表 4、数组与链表的区别 5、链表的增删查 5.1、在头部插入链表 5.2、在中间插入链表 5.3、删除头节点 5.4、删除中间节点 5.5、查询某个值 6、链表的应用 6.1 如何设计一个LRU缓存算法? 6.2 约瑟夫问题 1、链表的定…...
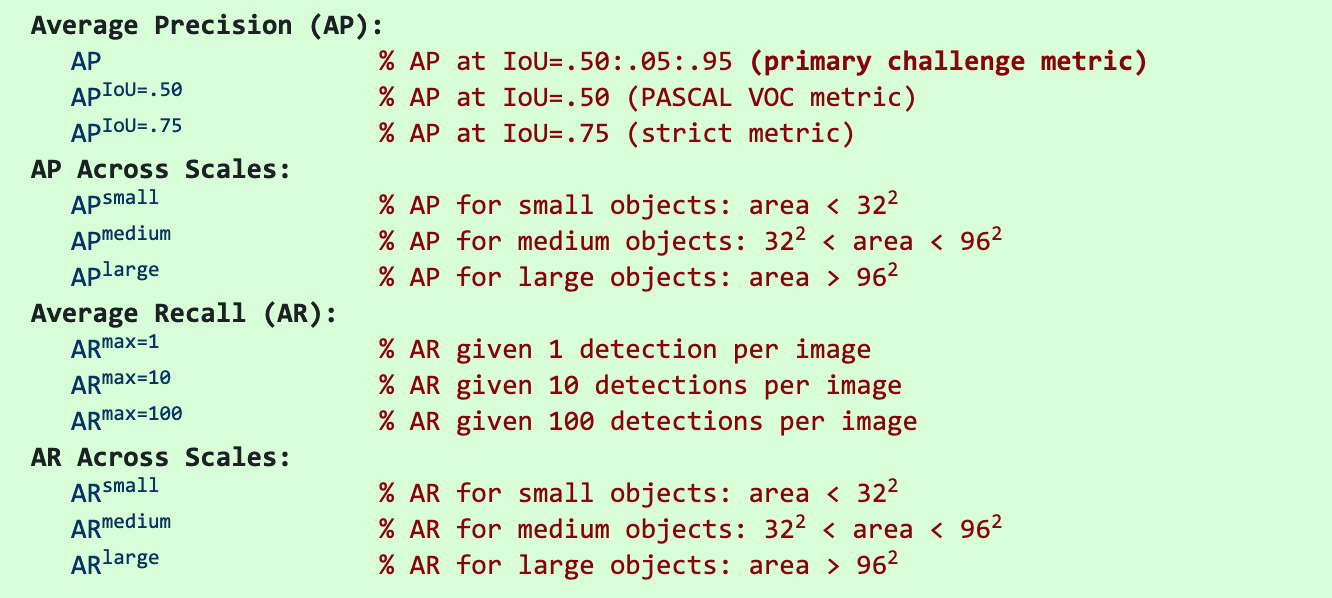
目标检测COCO数据集与评价体系mAP
1.mAP 2.IoU IoU也就是交并比,也称为 Jaccard 指数,用于计算真实边界框与预测边界框之间的重叠程度。它是真值框与预测边界框的交集和并集之间的比值。Ground Truth边界框是测试集中手工标记的边界框,用于指定对象图像的位置以及预测的边界框…...

2024最全面且有知识深度的web3开发工具、web3学习项目资源平台
在Web3技术迅速发展的时代,寻找一个综合且深入的Web3开发工具和学习项目资源平台变得至关重要。今天,我将向大家介绍一个非常有价值的网站,它就是https://web3x.world 。 Web3X是一个全面而深入的Web3开发者社区,为开发者们提供了…...

Golang - defer关键字 深入剖析
defer关键字 defer和go一样都是Go语言提供的关键字。defer用于资源的释放,会在函数返回之前进行调用。一般采用如下模式: f,err : os.Open(filename) if err ! nil {panic(err) } defer f.Close()如果有多个defer表达式,调用顺序类似于栈&a…...

如何在Spring Boot中使用@Scheduled写定时任务判断数据量是否过大,过大则进行分表操作,多张表使用临时视图查询
当数据量过大,在定时任务中执行分表操作 1、复制表结构及数据 在xml中编写复制表结构及数据(newTableName为新表名、originalTableName为原始表名) 只复制表结构: CREATE TABLE ${newTableName} AS SELECT * FROM ${originalTa…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...

