代码随想录day20 开始二叉搜索树
654.最大二叉树
题目
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下:
- 二叉树的根是数组中的最大元素。
- 左子树是通过数组中最大值左边部分构造出的最大二叉树。
- 右子树是通过数组中最大值右边部分构造出的最大二叉树。
通过给定的数组构建最大二叉树,并且输出这个树的根节点。
示例 :

思考
本题也是通过递归的方式构造二叉树:找到数组中最大的数,然后最大数左部分变成一个数组,右部分变成一个数组,继续node->left、node->right递归两个数组,注意创建左右数组的时候需要跳过node
代码
class Solution {
public:
TreeNode* traversal(vector<int>& nums) {
if(nums.size() == 0) return nullptr;
int maxValue = INT_MIN;
for(auto i : nums) {
maxValue = max(maxValue, i);
}
TreeNode* node = new TreeNode(maxValue);
int pos = 0;
for(; pos < nums.size(); pos++) {
if(nums[pos] == maxValue) break;
}
vector<int> left(nums.begin(), nums.begin() + pos);
vector<int> right(nums.begin() + pos + 1, nums.end());
node->left = traversal(left);
node->right = traversal(right);
return node;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return traversal(nums);
}
};
617.合并二叉树
题目
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:

注意: 合并必须从两个树的根节点开始。
思考
想了很久怎么用层序遍历做,卡在了如果tree1和tree2的层数不一样该怎么遍历,看了解题答案发现其实就是把tree1和tree2的两个结点都存入que即可,同时并不需要计算size,因为可以用tree1来代替new TreeNode,这里需要判断四个情况,node1->left != nullptr && node2->left != nullptr、node1->right != nullptr && node2->right != nullptr、node1->left == nullptr && node2->left != nullptr、node1->right == nullptr && node2->right != nullptr。
代码
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if(root1 == nullptr) return root2;
if(root2 == nullptr) return root1;
queue<TreeNode*> que;
que.push(root1);
que.push(root2);
while(!que.empty()) {
TreeNode* node1 = que.front();
que.pop();
TreeNode* node2 = que.front();
que.pop();
node1->val += node2->val;
if(node1->left != nullptr && node2->left != nullptr) {
que.push(node1->left);
que.push(node2->left);
}
if(node1->right != nullptr && node2->right != nullptr) {
que.push(node1->right);
que.push(node2->right);
}
if(node1->left == nullptr && node2->left != nullptr) node1->left = node2->left;
if(node1->right == nullptr && node2->right != nullptr) node1->right = node2->right;
}
return root1;
}
};
700.二叉搜索树中的搜索
题目
给定二叉搜索树(BST)的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 NULL。
例如,

在上述示例中,如果要找的值是 5,但因为没有节点值为 5,我们应该返回 NULL。
思考
开始二叉搜索树啦,其实二叉搜索树定义很简单,一个结点的左子树所有结点都比它小,右子树的所有结点都比它大,本题其实就是找到一个二叉搜索树的子树,如果这个结点大于给定val,那么root = root->right,如果小于,那么root = root->left,如果等于就return root; 注意这里要用while(root != null)来做循环持续判断root
代码
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
while(root != NULL) {
if(root->val > val) root = root->left;
else if(root->val < val) root = root-> right;
else return root;
}
return NULL;
}
};
98.验证二叉搜索树
题目
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。

思考
这题陷入了一个常见的误区,就是没有判断该结点左右子树的所有元素都小于或大于该结点,而仅仅判断了该结点的左右结点,看了卡哥的视频,才发现二叉搜索树需要用中序遍历来写:
1、用中序遍历来将二叉树变成一个数组,然后判断这个数组是不是递增排布的
2、创建一个值为最小值的maxValue,用中序遍历来将每一个结点都与maxValue进行判断,如果大于它,那么mavValue的值就被该结点的值取代,如果小于,就return false,因为二叉搜索树左中右是递增关系
代码
class Solution {
public:
long long maxValue = LONG_MIN;
bool isValidBST(TreeNode* root) {
if(root == nullptr) return true;
bool left = isValidBST(root->left);
if(root->val > maxValue) maxValue = root->val;
else return false;
bool right = isValidBST(root->right);
return left && right;
}
};
相关文章:

代码随想录day20 开始二叉搜索树
654.最大二叉树 题目 给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下: 二叉树的根是数组中的最大元素。左子树是通过数组中最大值左边部分构造出的最大二叉树。右子树是通过数组中最大值右边部分构造出的最大二叉树。 通过给定的数组构…...
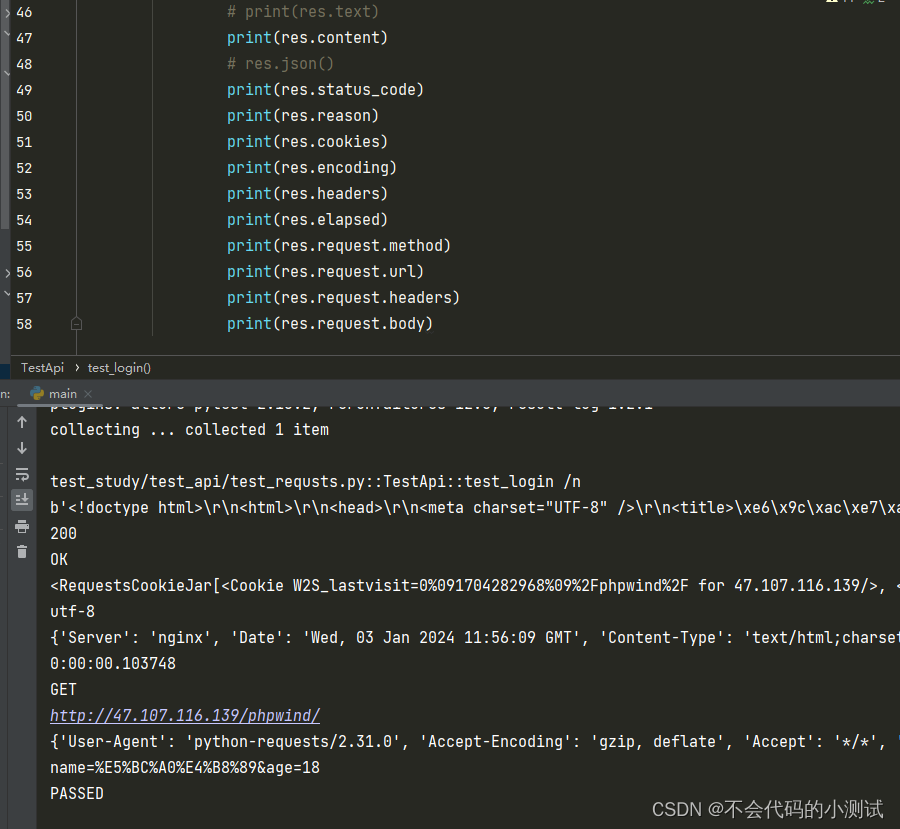
从0开始python学习-39.requsts库
目录 HTTP协议 1. 请求 2. 响应 Requests库 1. 安装 2. 请求方式 2.1 requests.请求方式(参数) 2.2 requests.request() 2.3 requests.session().request() 2.4 三种方式之间的关联 3. 请求参数 3.1 params:查询字符串参数 3.2 data:Form表单…...
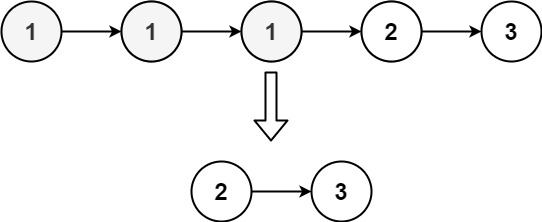
【面试高频算法解析】算法练习3 双指针
前言 本专栏旨在通过分类学习算法,使您能够牢固掌握不同算法的理论要点。通过策略性地练习精选的经典题目,帮助您深度理解每种算法,避免出现刷了很多算法题,还是一知半解的状态 专栏导航 二分查找回溯双指针滑动窗口深度优先搜索…...

React16源码: Why16, 研究源码的意义, 源码目录核心结构分析
为什么要选择React16 现在React18都早已实践很多,为何回过头来看16版本的代码理由如下 从实际出发,企业内老旧项目多为16版本,理解16的核心能够帮助我们快速解决问题16版本React是完全重写了核心代码, 是一次重大的更新 引入了 fiber 这个概…...

mybatis-flex笔记
MyBatis-Flex 的增删改功能 - MyBatis-Flex 官方网站https://mybatis-flex.com/zh/base/add-delete-update.html 代码https://gitee.com/hntianshu/mybatis-flex-test 一 新增数据 不忽略 null 值。 就是允许有null 忽略null 就是不允许有null BaseMapper 的接口提供了 inser…...

Debezium发布历史47
原文地址: https://debezium.io/blog/2019/02/13/debezium-0-9-1-final-released/ 欢迎关注留言,我是收集整理小能手,工具翻译,仅供参考,笔芯笔芯. Debezium 0.9.1.Final 发布 二月 13, 2019 作者: Gunna…...

Python爬虫抓包常见问题解决
对于Python爬虫和Fiddler抓包,可能遇到的问题及解决: 代理设置错误:如果你在使用Python爬虫时遇到抓不到包的问题,首先应该检查你的浏览器代理设置是否正确。以Chrome为例,代理设置为:右上角菜单按钮>设…...

c++跨平台ui
fltk https://gitee.com/mirrors_fltk/fltk.git codeblock中有fltk项目开发模板,可以快速构建项目 wxwidget https://gitee.com/sofu456/wxWidgets.git git submodule update --init --recursive 打开demo和sample set(wxBUILD_SAMPLES ALL) set(wxBUILD_DEMOS ON) build/…...

stable diffusion 基础教程-提示词之艺术风格用法
展现夕阳 golden hour, (rim lighting):1.2, warm tones, sun flare, soft shadows, vibrant colors, hazy glow, painterly effect, dreamy atmosphere阴影 chiaroscuro, (high contrast):1.2, dramatic shadows, bold highlights, moody atmosphere, captivating inte…...

【日积月累】Java中 正则表达式
目录 日积月累】Java中 正则表达式 1.前言2.基本语法3.Pattern和Matcher类4.校验的表达式大全5.参考文章所属专区 日积月累 1.前言 正则表达式是一种用于匹配文本模式的语法,它通常与编程语言一起使用。在Java中,正则表达式用于匹配字符串,可以使用Pattern和Matcher类来实…...

Java调用百度云语音识别【音频转写】
百度云文档 ttps://ai.baidu.com/ai-doc/SPEECH/Bk5difx01 示例代码: import com.alibaba.fastjson.JSON; import com.alibaba.fastjson.JSONArray; import lombok.extern.slf4j.Slf4j; import okhttp3.*; import org.json.JSONObject; import org.springframework.stereotyp…...
pyparamvalidate 项目背景和需求分析
目录 一、前置说明1、总体目录2、本节目标 二、项目背景三、需求分析三、后置说明1、要点小结2、下节预告 一、前置说明 1、总体目录 《 pyparamvalidate 参数校验器,从编码到发布全过程》 2、本节目标 阐述 pyparamvalidate 项目背景和需求分析。 二、项目背景…...

Docker Linux快速安装及Nginx部署
前言 最近正在部署一套新的Linux服务器环境,基于Docker来部署所有的应用,顺便整理了一套经过验证的操作手册,以便大家遇到类似需求时,可以直接拿来用。 本文会涉及以下知识点:Docker的Linux安装和卸载、Docker用户组…...
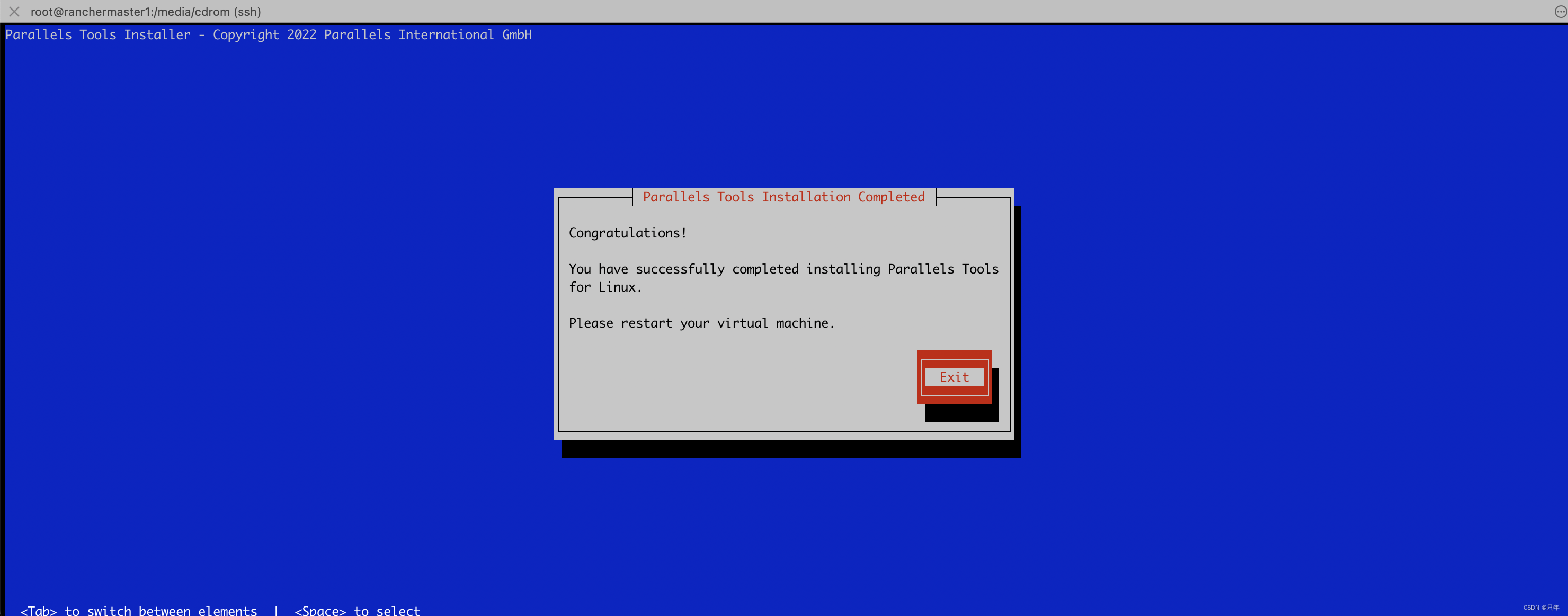
Mac M1 Parallels CentOS7.9 Install Parallels Tools
一、挂载parallels-tools安装包 mkdir /media/cdrom/ mount /dev/cdrom /media/cdrom/ mount: /dev/sr0 写保护,将以只读方式挂载二、GCC升级 yum install -y centos-release-scl yum install -y devtoolset-8-gcc*# 切换当前会话中gcc版本为8 scl enable devtool…...
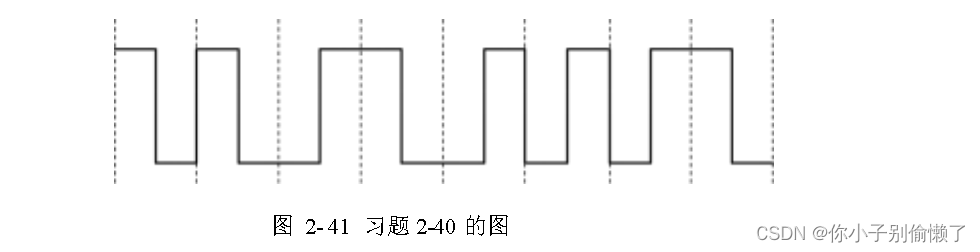
计算机网络物理层 习题答案及解析
2-1 下列选项中,不属于物理层接口规范定义范畴的是( D )。 A. 引脚功能 B. 接口形状 C. 信号电平 D. 传输媒体 【答案】D 【解析】 2-2 某网络在物理层规定,信号的电平范围为- 15V~15V , 电线长…...
【解决】Unity 设置跨设备分辨率表现
开发平台:Unity 2018版本以上 开发语言:CSharp 编程平台:Visual Studio 2022 问题描述 使用 UnityEngine.dll 中关于设置分辨率的方法时,无法满足应用以设定分辨率进行屏幕显示问题。因而造成画面不同程度的拉伸情况。而这种情…...

基于单片机的智能衣柜设计
一、摘要 随着科技的不断发展,人们对于生活品质的要求越来越高。智能衣柜作为智能家居的一个重要组成部分,能够为用户提供便捷、个性化的衣物管理服务。本文主要研究了基于单片机的智能衣柜设计,通过对硬件系统和软件系统的设计与实现&#…...

HttpSession的使用
1 HttpSession 概述 在 Java Servlet API 中引入 session 机制来跟踪客户的状态。session 指的是在一段时间内,单个客户与 Web 服务器的一连串相关的交互过程。在一个 session 中,客户可能会多次请求访问同一个网页,也有可能请求访问各种不同…...

人工智能在金融领域的应用存在的4大挑战
金融服务供应商应该有计划地应对AI面临的难题 金融行业投资人工智能热潮带来有关数据安全和透明度的新问题。由于数据管理实践随着新的 AI 解决方案的引入而不断发展,应对这些新问题以及金融服务领域 AI 面临的其他挑战尤为重要。各组织必须认识到可能面临以下挑战…...

EasyExcel写出包含多个sheet页的Excel
https://blog.csdn.net/qq_38751895/article/details/131852740...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
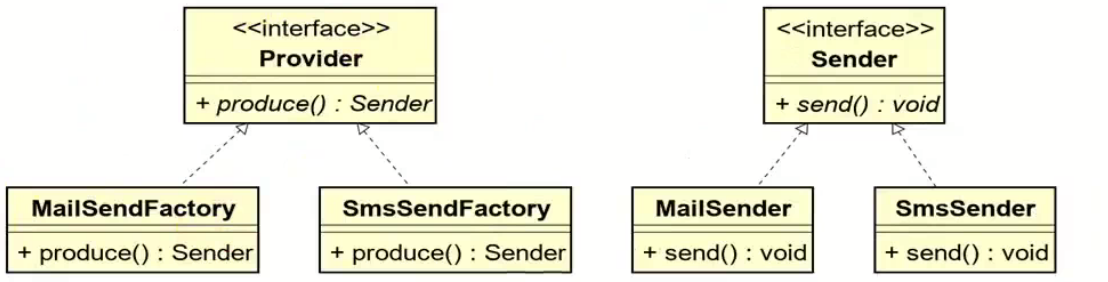
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...

【Pandas】pandas DataFrame dropna
Pandas2.2 DataFrame Missing data handling 方法描述DataFrame.fillna([value, method, axis, …])用于填充 DataFrame 中的缺失值(NaN)DataFrame.backfill(*[, axis, inplace, …])用于**使用后向填充(即“下一个有效观测值”)…...

多模态大语言模型arxiv论文略读(110)
CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文标题:CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文作者:Hidehisa Arai, Keita Miwa, Kento Sasaki, Yu Yamaguchi, …...

【笔记】结合 Conda任意创建和配置不同 Python 版本的双轨隔离的 Poetry 虚拟环境
如何结合 Conda 任意创建和配置不同 Python 版本的双轨隔离的Poetry 虚拟环境? 在 Python 开发中,为不同项目配置独立且适配的虚拟环境至关重要。结合 Conda 和 Poetry 工具,能高效创建不同 Python 版本的 Poetry 虚拟环境,接下来…...

Modbus转ETHERNET IP网关:快速冷却系统的智能化升级密钥
现代工业自动化系统中,无锡耐特森Modbus转Ethernet IP网关MCN-EN3001扮演着至关重要的角色。通过这一技术,传统的串行通讯协议Modbus得以在更高速、更稳定的以太网环境中运行,为快速冷却系统等关键设施的自动化控制提供了强有力的支撑。快速冷…...

【笔记】PyCharm 使用问题反馈与官方进展速览
#工作记录 https://youtrack.jetbrains.com/issue/IJPL-190308 【笔记】记一次PyCharm的问题反馈_the polyglot context is using an implementation th-CSDN博客 【笔记】与PyCharm官方沟通解决开发环境问题-CSDN博客 与 JetBrains 官方沟通记录(PyCharm 相关问题…...

前端验证下跨域问题(npm验证)
文章目录 一、背景二、效果展示三、代码展示3.1)index.html3.2)package.json3.3) service.js3.4)service2.js 四、使用说明4.1)安装依赖4.2)启动服务器4.3)访问前端页面 五、跨域解决方案说明六…...
