DS|树结构及应用
题目一:DS树 -- 树的先根遍历(双亲转先序)
题目描述:
给出一棵树的双亲表示法结果,用一个二维数组表示,位置下标从0开始,如果双亲位置为-1则表示该结点为根结点
编写程序,输出该树的先根遍历结果。
输入要求:
第一个输入t,表示有t棵树
接着每棵树输入3行:
第1行输入n,表示树有n个结点
第2行输入n个英文字母,表示每个树结点的数值
第3行输入n个整数,表示每个结点的双亲在数组的下标
以此类推输入下一棵树
输出要求:
共输出t行,每行输出一棵树的先根遍历结果
输入样例:
2
7
A B C D E F G
-1 0 0 0 1 1 3
10
A B C D R E F G H K
4 4 4 0 -1 0 2 6 6 6
输出样例:
ABEFCDG
RADEBCFGHK代码示例:
#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;const int N = 10010;struct TNode {char data;int parent;
};struct Tree {TNode node[N];int n;
};void CreateTree(Tree& t) {cin >> t.n;for (int i = 0; i < t.n; i++) cin >> t.node[i].data;for (int i = 0; i < t.n; i++) cin >> t.node[i].parent;
}void PreOrder(Tree t, int x) {for (int i = 0; i < t.n; i++) {if (t.node[i].parent == x) {cout << t.node[i].data;PreOrder(t, i);}}
}
int main() {int t;cin >> t;while (t--) {Tree tree;CreateTree(tree);PreOrder(tree, -1);cout << endl;}
}题目二:DS树 -- 树的后根遍历(孩子链表法)
题目描述:
根据树的孩子链表表示法构建一棵树,并输出树的后根遍历
下标位置从0开始
输入要求:
第一行输入两个参数,第一个参数n表示树有n个结点,第二个参数r表示根结点的数组下标
接着n行,每行先输入一个结点的数值(用单个字母表示),再输入结点的孩子的下标,最后以-1结尾
如果该结点没有孩子,则一行只输入结点的数值和-1
输出要求:
只有一行输出,树的后根遍历结果
输入样例:
10 4
A 3 5 -1
B -1
C 6 -1
D -1
R 0 1 2 -1
E -1
F 7 8 9 -1
G -1
H -1
K -1
输出样例:
DEABGHKFCR代码示例:
#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;const int N = 110;struct TNode {char data;int child[110];
};struct Tree {TNode node[N];
};void CreateTree(Tree& t, int n) {for (int i = 0; i < n; i++) {cin >> t.node[i].data;for (int j = 0;; j++) {cin >> t.node[i].child[j];if (t.node[i].child[j] == -1) break;}}
}void Postorder(Tree t, int x) {for (int i = 0; t.node[x].child[i] != -1; i++) Postorder(t, t.node[x].child[i]);cout << t.node[x].data;
}int main() {int n, r;cin >> n >> r;Tree tree;CreateTree(tree, n);Postorder(tree, r);cout << endl;return 0;
}题目三:DS树 -- 树结构转换(先序转双亲)
题目描述:
给出一棵二叉树的特定字符先序遍历结果(空子树用字符'#'表示),构建该二叉树,并输出该二叉树的双亲表示法结果
双亲表示法的数组下标从0开始,根结点必定是在下标0元素,且根结点的双亲下标为-1,左右孩子按下标递增顺序排列,
结点下标是层次遍历顺序。
输入要求:
第一个输入t,表示有t棵二叉树
接着t行,每行输入含特定字符的二叉树先序遍历序列
输出要求:
共输出2t行
每棵二叉树输出两行,第一行输出各个结点的数值,第二行输出各结点的双亲下标
输入样例:
3
AB#C##D##
ABD##E##C##
AB##CDW###E#F##输出样例:
A B D C
-1 0 0 1
A B C D E
-1 0 0 1 1
A B C D E W F
-1 0 0 2 2 3 4代码示例:
#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;struct BNode {char data;BNode* lChild;BNode* rChild;BNode* Parent;
};class BTree {
public:BNode* root;BNode* node[100];int pos[100];//双亲下标int len;//两个数组的长度BTree() :root(NULL) {}BNode* creatBTree(BNode* father) {BNode* tmp;char ch;cin >> ch;if (ch == '#') tmp = NULL;else {tmp = new BNode;tmp->data = ch;tmp->Parent = father;tmp->lChild = creatBTree(tmp);tmp->rChild = creatBTree(tmp);}return tmp;}int findNode(BNode* btn){if (btn == NULL) return -1;for (int i = 0; i <= 100; i++) if (btn == node[i]) return i;}void BFS(){queue<BNode*> q;int index = 0;if (root != nullptr) {q.push(root);while (!q.empty()) {node[index] = q.front();pos[index] = findNode(q.front()->Parent);index++;if (q.front()->lChild != NULL) q.push(q.front()->lChild);if (q.front()->rChild != NULL) q.push(q.front()->rChild);q.pop();}}len = index;}void Display(){for (int i = 0; i < len; i++) {cout << node[i]->data;if (i == len - 1) cout << endl;else cout << " ";}for (int i = 0; i < len; i++){cout << pos[i];if (i == len - 1) cout << endl;else cout << " ";}}
};int main() {int t;cin >> t;while (t--) {BTree tree;tree.root = tree.creatBTree(NULL);tree.BFS();tree.Display();}
}题目四:DS树 -- 树结构转换(双亲转孩子链表)
题目描述:
给出一棵树的双亲表示法结果,用一个二维数组表示,位置下标从0开始,如果双亲位置为-1则表示该结点为根结点
编写程序,输出该树的孩子链表表示法结果。
输入要求:
输入一棵树的双亲表示法,共3行:
第1行输入n,表示树有n个结点
第2行输入n个英文字母,表示每个树结点的数值
第3行输入n个整数,表示每个结点的双亲在数组的下标
输出要求:
按输入的结点顺序输出n行,每行输出结点孩子链表结果,先输出结点的数值,再输出结点的孩子的下标,以空格隔开,最后一个数据后面也有空格
如果链表为空则输出结点数值后,输出-1带空格,具体看样式
输入样例:
7
A B C D E F G
-1 0 0 0 1 1 3输出样例:
A 1 2 3
B 4 5
C -1
D 6
E -1
F -1
G -1 代码示例:
#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;const int N = 110;struct TNode {char data;int parent;
};struct Tree {TNode node[N];int n;
};void createTree(Tree& tree) {cin >> tree.n;for (int i = 0; i < tree.n; i++) cin >> tree.node[i].data;for (int i = 0; i < tree.n; i++) cin >> tree.node[i].parent;
}void Display(Tree tree) {for (int i = 0; i < tree.n; i++) {cout << tree.node[i].data << " ";bool mark = false;for (int j = 0; j < tree.n; j++) {if (tree.node[j].parent == i) {mark = true;cout << j << " ";}}if (!mark) cout << "-1 ";cout << endl;}
}int main() {Tree tree;createTree(tree);Display(tree);
}题目五:DS树 -- 森林叶子编码
题目描述:
给定一组森林,编写程序生成对应的二叉树,输出这颗二叉树叶结点对应的二进制编码.规定二叉树的左边由0表示,二叉树的右边由1表示。
输入要求:
N B 表示N个树,每结点最多B个分支
第2行至第N+1行,每个树的先序遍历
输出要求:
每行表示一个叶结点对应的二进制编码
输入样例:
3 3
A B 0 0 0 C 0 0 0 D 0 0 0
E F 0 0 0 0 0
G H 0 0 0 I J 0 0 0 0 0 0
输出样例:
0 1 1
1 0
1 1 0 1 0代码示例:
#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
using namespace std;int B, N;struct BTNode {char data;BTNode* lChild;BTNode* rChild;
};struct TNode {char e;TNode** Child;TNode() {Child = new TNode * [B];for (int i = 0; i < B; i++) Child[i] = NULL;}
};
class Tree {
private:TNode* root;//创建一般树TNode* createTree() {TNode* T = NULL;char ch;cin >> ch;if (ch != '0') {T = new TNode();T->e = ch;for (int i = 0; i < B; i++) T->Child[i] = createTree();}return T;}//转化成根节点没有右子树的二叉树BTNode* Trans(TNode* T) {BTNode* p = NULL;if (T){p = new BTNode;p->data = T->e;int cnt = 0;while (!T->Child[cnt] && cnt < B) cnt++;if (cnt == B) p->lChild = Trans(NULL);else p->lChild = Trans(T->Child[cnt]);if (p->lChild){BTNode* q = p->lChild;for (int i = cnt + 1; i < B; i++){q->rChild = Trans(T->Child[i]);if (q->rChild) q = q->rChild;}}}return p;}
public://生成树void Create() { root = createTree(); }BTNode* Trans() { return Trans(root); }
};
class BTree {
private:BTNode* root;//二叉树的编码输出void print(BTNode* t, string s) {if (t) {if (t->lChild == NULL && t->rChild == NULL) {s = s.substr(0, s.size() - 1);cout << s << endl;}print(t->lChild, s + "0 ");print(t->rChild, s + "1 ");}}
public:BTree() {}//将森林合成二叉树void emerge(BTNode** t) {root = t[0];for (int i = 0; i < N - 1; i++) t[i]->rChild = t[i + 1];}//编码输出void print() {string str = "";print(root, str);}
};int main() {cin >> N >> B;Tree* ts = new Tree[N];BTNode** btn = new BTNode * [N];//读取一般树for (int i = 0; i < N; i++) ts[i].Create();//把每个一般树转化成不含有右子树二叉树for (int i = 0; i < N; i++) btn[i] = ts[i].Trans();BTree btree;//将不含右子树的二叉树合并btree.emerge(btn);btree.print();return 0;
}题目六:先序+中序还原二叉树
题目描述:
给定一棵二叉树的先序遍历序列和中序遍历序列,要求计算该二叉树的高度。
输入要求:
输入首先给出正整数N(≤50),为树中结点总数。下面两行先后给出先序和中序遍历序列,均是长度为N的不包含重复英文字母(区别大小写)的字符串。
输出要求:
输出为一个整数,即该二叉树的高度。
输入样例:
9
ABDFGHIEC
FDHGIBEAC输出样例:
5代码示例:
简单求解,只针对还原后求高度:
#include <iostream>
using namespace std;int DFS(char* pre, char* in, int n) {if (n == 0) return 0;int i;for (i = 0; i < n; i++) if (in[i] == pre[0]) break;int left = DFS(pre + 1, in, i);int right = DFS(pre + i + 1, in + i + 1, n - i - 1);return max(left, right) + 1;
}int main() {int n;cin >> n;char* pre = new char[n];char* in = new char[n];cin >> pre >> in;cout << DFS(pre, in, n);return 0;
}正常还原树方法:
#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;struct BNode {char data;BNode* lChild;BNode* rChild;
};class BTree {
public:BNode* root;BTree() :root(NULL) {}BNode* creatBTree() {BNode* tmp;char ch;cin >> ch;if (ch == '0') tmp = NULL;else {tmp = new BNode;tmp->data = ch;tmp->lChild = creatBTree();tmp->rChild = creatBTree();}return tmp;}void Preorder(BNode* cur) {if (cur != NULL) {cout << cur->data;Preorder(cur->lChild), Preorder(cur->rChild);}}void Inorder(BNode* cur) {if (cur != NULL) {Inorder(cur->lChild);cout << cur->data;Inorder(cur->rChild);}}void Postorder(BNode* cur) {if (cur != NULL) {Postorder(cur->lChild), Postorder(cur->rChild);cout << cur->data;}}int TreeHeight(BNode* cur) {if (cur == NULL) return 0;else return max(TreeHeight(cur->lChild), TreeHeight(cur->rChild)) + 1;}BNode* getTree(vector<char>& preStr, vector<char>& inStr) {if (preStr.empty()) return NULL;BNode* root = new BNode();root->data = preStr[0];vector<char>::iterator mid = find(inStr.begin(), inStr.end(), preStr[0]);int left_nodes = mid - inStr.begin();vector<char> left_inStr(inStr.begin(), mid);vector<char> right_inStr(mid + 1, inStr.end());vector<char> left_preStr(preStr.begin() + 1, preStr.begin() + 1 + left_nodes);vector<char> right_preStr(preStr.begin() + 1 + left_nodes, preStr.end());root->lChild = getTree(left_preStr, left_inStr);root->rChild = getTree(right_preStr, right_inStr);return root;}
};vector<char> getCharArray(string str) {vector<char> res;for (char c : str) res.push_back(c);return res;
}int main() {string preOrder;string inOrder;int nodeCount;//本题给出了结点总数,要求输入那就输出进来,防止报错,实际并没有用到;cin >> nodeCount;cin >> preOrder >> inOrder;vector<char> preStr = getCharArray(preOrder);vector<char> inStr = getCharArray(inOrder);BTree tree;tree.root = tree.getTree(preStr, inStr);cout << tree.TreeHeight(tree.root) << endl;return 0;
}根据后序+中序还原二叉树(先输入后序结果):
#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;struct BNode {char data;BNode* lChild;BNode* rChild;
};class BTree {
public:BNode* root;BTree() :root(NULL) {}BNode* creatBTree() {BNode* tmp;char ch;cin >> ch;if (ch == '0') tmp = NULL;else {tmp = new BNode;tmp->data = ch;tmp->lChild = creatBTree();tmp->rChild = creatBTree();}return tmp;}void Preorder(BNode* cur) {if (cur != NULL) {cout << cur->data;Preorder(cur->lChild), Preorder(cur->rChild);}}void Inorder(BNode* cur) {if (cur != NULL) {Inorder(cur->lChild);cout << cur->data;Inorder(cur->rChild);}}void Postorder(BNode* cur) {if (cur != NULL) {Postorder(cur->lChild), Postorder(cur->rChild);cout << cur->data;}}int TreeHeight(BNode* cur) {if (cur == NULL) return 0;else return max(TreeHeight(cur->lChild), TreeHeight(cur->rChild)) + 1;}BNode* getTree(vector<char>& postStr, vector<char>& inStr) {if (postStr.empty()) return NULL;BNode* root = new BNode();root->data = postStr[postStr.size() - 1];vector<char>::iterator mid = find(inStr.begin(), inStr.end(), postStr[postStr.size() - 1]);int left_nodes = mid - inStr.begin();vector<char> left_inStr(inStr.begin(), mid);vector<char> right_inStr(mid + 1, inStr.end());vector<char> left_postStr(postStr.begin(), postStr.begin() + left_nodes);vector<char> right_postStr(postStr.begin() + left_nodes , postStr.end() - 1);root->lChild = getTree(left_postStr, left_inStr);root->rChild = getTree(right_postStr, right_inStr);return root;}
};vector<char> getCharArray(string str) {vector<char> res;for (char c : str) res.push_back(c);return res;
}int main() {string postOrder;string inOrder;cin >> postOrder >> inOrder;vector<char> postStr = getCharArray(postOrder);vector<char> inStr = getCharArray(inOrder);BTree tree;tree.root = tree.getTree(postStr, inStr);tree.Preorder(tree.root);cout << endl;return 0;
}相关文章:

DS|树结构及应用
题目一:DS树 -- 树的先根遍历(双亲转先序) 题目描述: 给出一棵树的双亲表示法结果,用一个二维数组表示,位置下标从0开始,如果双亲位置为-1则表示该结点为根结点 编写程序,输出该树…...
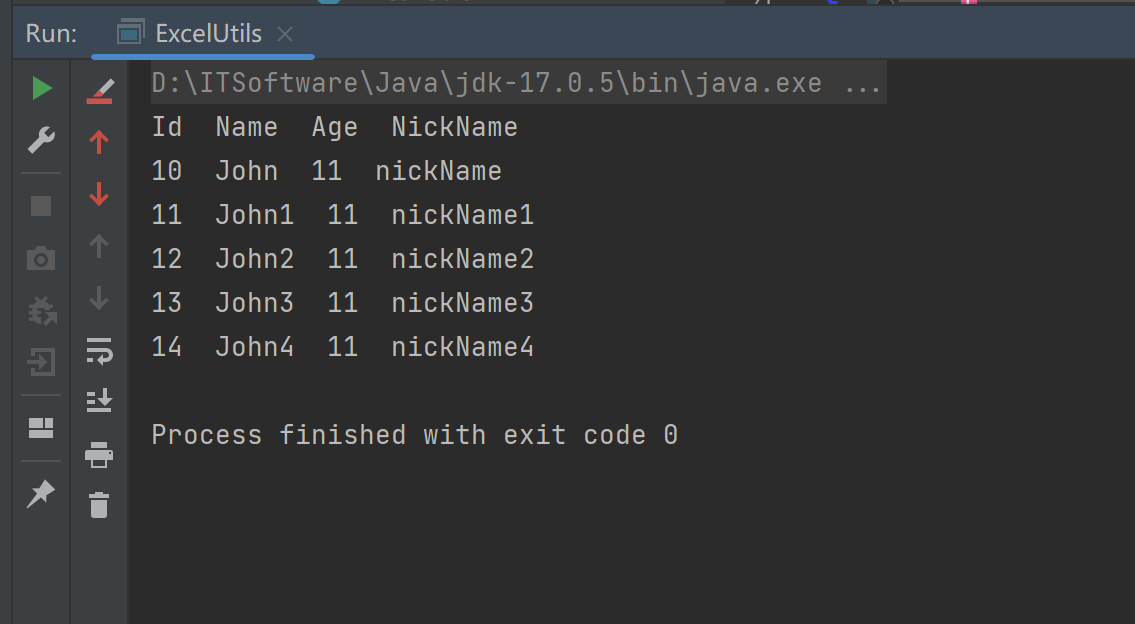
Java 读取超大excel文件
注意:此参考解决方案只是针对xlsx格式的excel文件! Maven <dependency><groupId>com.monitorjbl</groupId><artifactId>xlsx-streamer</artifactId><version>2.2.0</version> </dependency>读取方式1…...

K8S中的job和CronJob
Job 介绍 Kubernetes jobs主要是针对短时和批量的工作负载。它是为了结束而运行的,而不是像deployment、replicasets、replication controllers和DaemonSets等其他对象那样持续运行。 示例 apiVersion: batch/v1 kind: Job metadata:name: pispec:template:spec:r…...
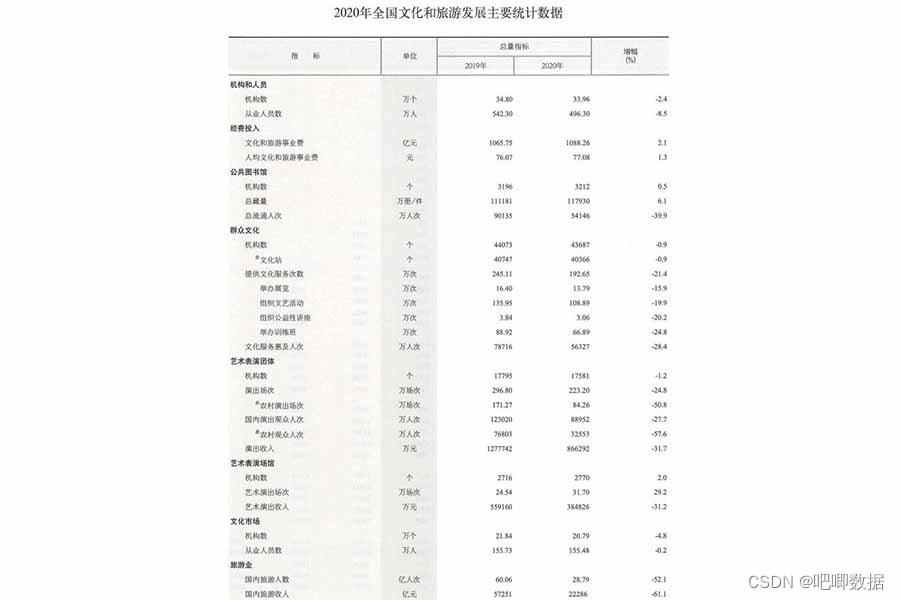
中国文化文物和旅游统计年鉴,数据含pdf、excel等格式,文本形式呈现,可预览数据
基本信息. 数据名称: 中国旅游统计年鉴 数据格式: pdf、xls不定 数据时间: 2012-2020年 数据几何类型: 文本 数据坐标系: —— 数据来源:文化和旅游部、网络公开数据 原名为《中国旅游统计年鉴》2020年后更名为《中国文化文物和旅游统计年鉴》ÿ…...
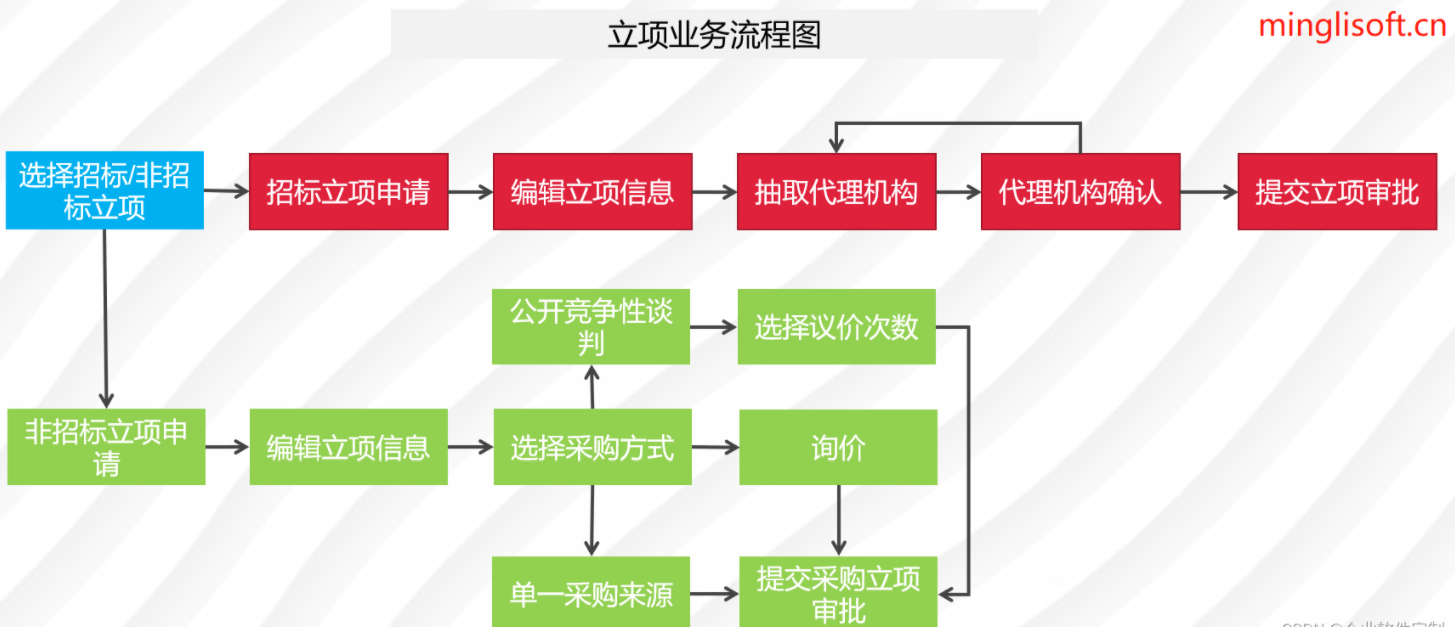
Java版企业电子招标采购系统源码——鸿鹄电子招投标系统的技术特点
在数字化时代,采购管理也正经历着前所未有的变革。全过程数字化采购管理成为了企业追求高效、透明和规范的关键。该系统通过Spring Cloud、Spring Boot2、Mybatis等先进技术,打造了从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通过…...

go语言语法基础
文章目录 前言一、输入和输出常用的字符串格式化符号 二、注释三、Go常用基本语言数据类型数字类型布尔类型字符类型变量与常量数组和切片数组切片 map类型创建map增删改查特别提醒 指针 四、运算符五、条件判断语句if系列switch六、循环语句for循环标准写法死循环while循环do …...

eclipse 和java环境的安装教程
安装 Eclipse 和配置 Java 环境是一个多步骤的过程,涉及到安装 Java Development Kit (JDK) 和 Eclipse IDE。以下是基本步骤: 安装 Java Development Kit (JDK) 下载 JDK: 访问 Oracle 官方网站(Oracle JDK)或者选择…...

Win11系统的优化方法参考文档(彻底优化策略)
目录 一、个性化-应用-关闭防火墙等的设置 二、任务栏优化设置 三、Win11开始菜单更改为Win10经典菜单 四、将Micresoft Store 从固定任务栏取消 五、电源性能优化 六、解决卡顿 七、卸载系统自带软件 八、任务管理器开机启动项的禁用 九、调整为最佳性能 十…...
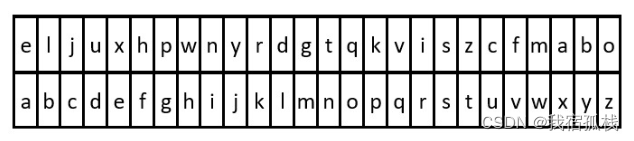
Leetcode13-解密消息(2325)
1、题目 给你字符串 key 和 message ,分别表示一个加密密钥和一段加密消息。解密 message 的步骤如下: 使用 key 中 26 个英文小写字母第一次出现的顺序作为替换表中的字母 顺序 。 将替换表与普通英文字母表对齐,形成对照表。 按照对照表 …...
二进制安装包安装Prometheus插件安装(mysql_exporter)
简介 mysql_exporter是用来收集MysQL或者Mariadb数据库相关指标的,mysql_exporter需要连接到数据库并有相关权限。既可以用二进制安装部署,也可以通过容器形式部署,但为了数据收集的准确性,推荐二进制安装。 一,下载安…...
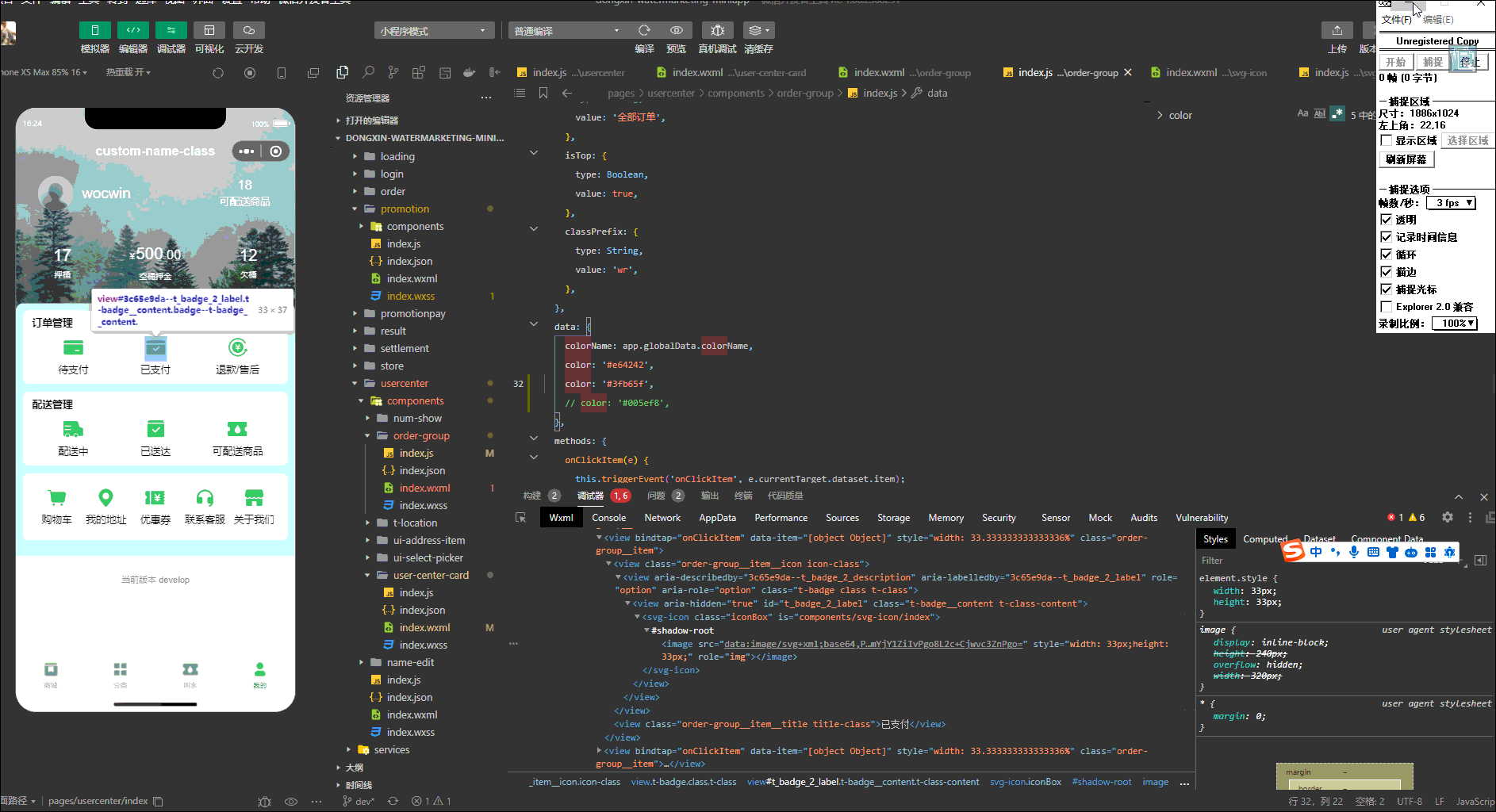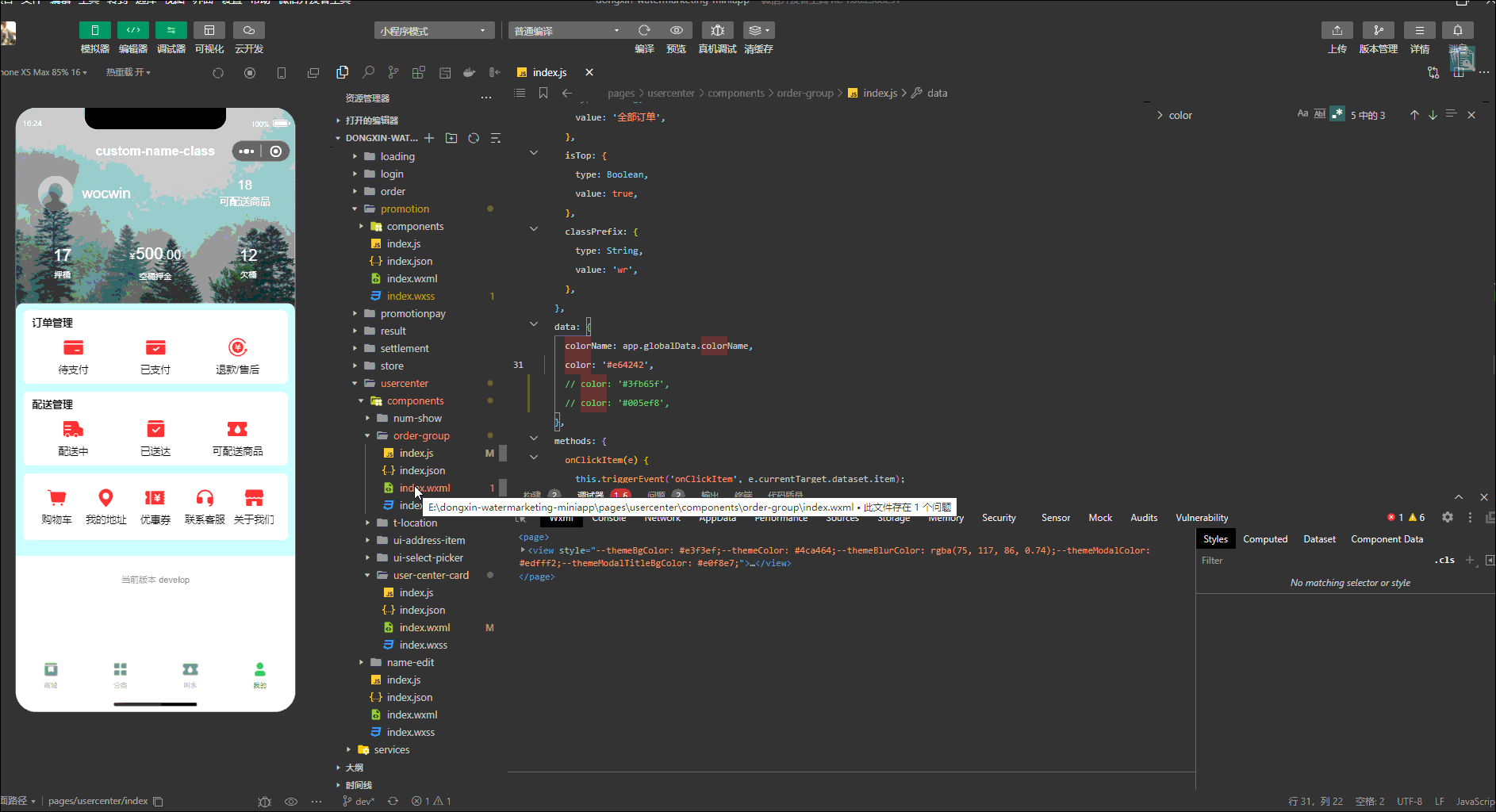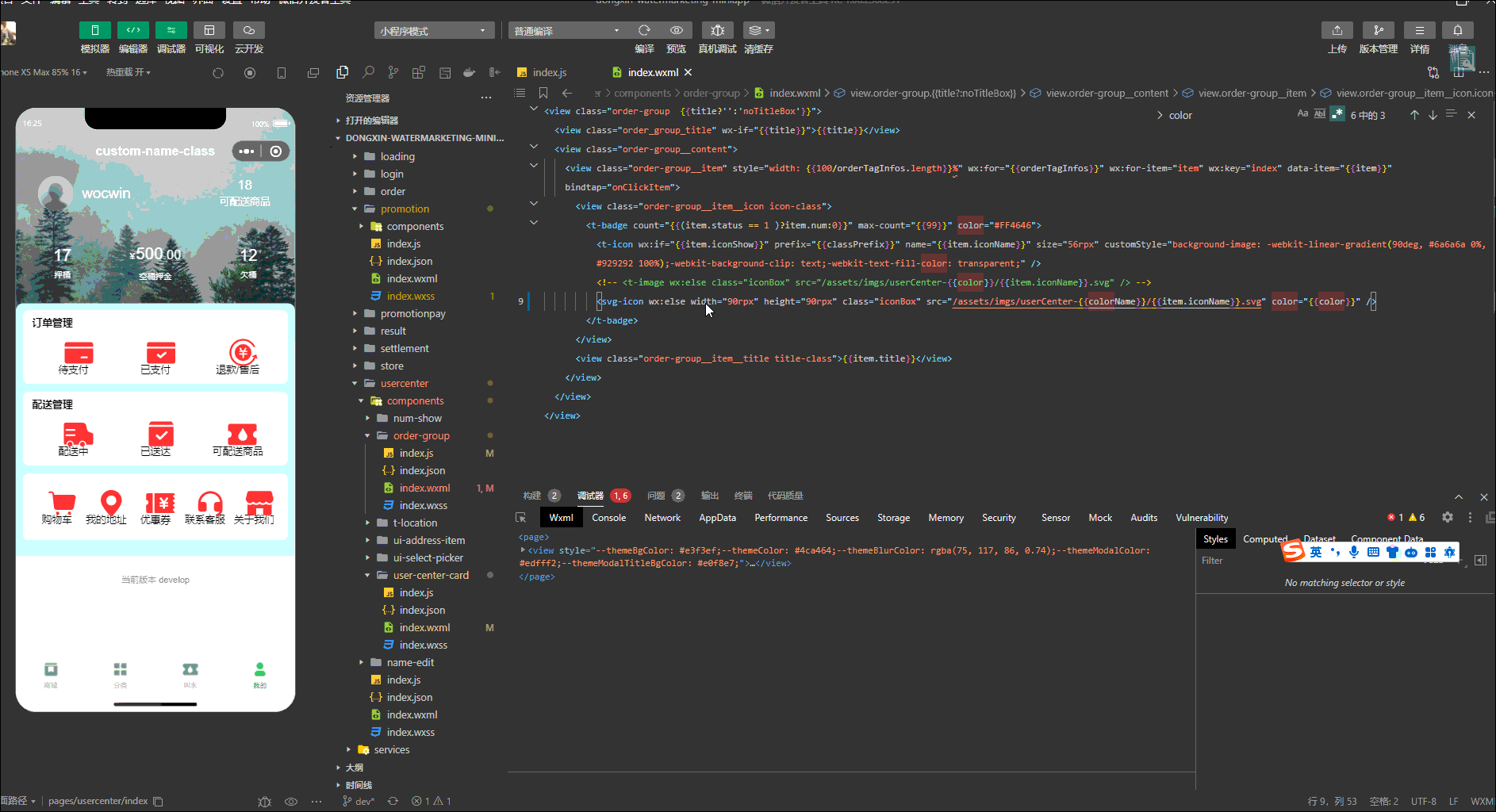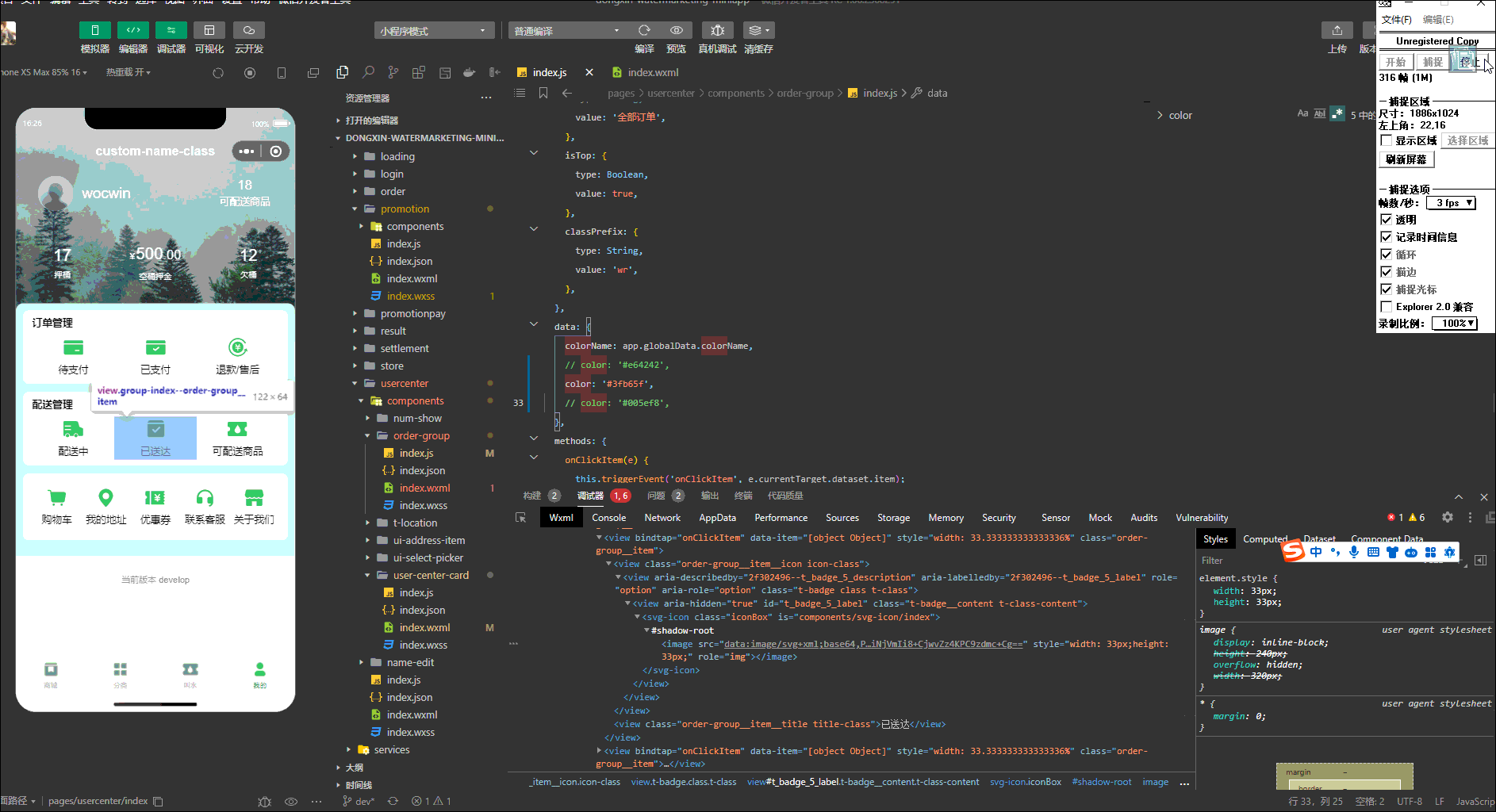
原生微信小程序如何动态修改svg图片颜色及尺寸、宽高(封装svgIcon组件)
最终效果 前言 动态设置Svg图片颜色就是修改Svg源码的path中的fill属性, 通过wx.getFileSystemManager().readFile读取.xlsx文件 把文件转成base64 封装svg-icon组件 1、在项目的components下新建svg-icon文件夹,新增base64.js文件 class Base64 {cons…...

Python从入门到网络爬虫(面向对象详解)
前言 Python从设计之初就已经是一门面向对象的语言,正因为如此,在Python中创建一个类和对象是很容易的。本章节我们将详细介绍Python的面向对象编程。如果你以前没有接触过面向对象的编程语言,那你可能需要先了解一些面向对象语言的一些基本…...
NPDP产品经理含金量高吗?难考吗?
NPDP的中文翻译为产品经理国际资格认证。NPDP考试起源于美国,由美国产品开发与管理协会(PDMA)发起。NPDP认证是集理论、方法与实践为一体的全方位知识体系,为公司组织层级进行规划、决策、执行提供良好的方法体系支撑。࿰…...

目标检测 YOLOv5 - 推理时的数据增强
目标检测 YOLOv5 - 推理时的数据增强 flyfish 版本 YOLOv5 6.2 参考地址 https://github.com/ultralytics/yolov5/issues/303在训练时可以使用数据增强,在推理阶段也可以使用数据增强 在测试使用数据增强有个名字叫做Test-Time Augmentation (TTA) 实际使用中使…...

篇二:springboot2.7 OAuth2 server使用jdbc存储RegisteredClient
上一篇 <<springboot 2.7 oauth server配置源码走读一>>中简单描述了oauth2 server的配置,其中使用了内存保存 RegisteredClient,本篇改用mysql存储。 db存储需要创建表,表结构应该是什么样的呢,从spring给我们封装好…...
卷积神经网络|导入图片
在学习卷积神经网络时,我们通常使用的就是公开的数据集,这里,我们不使用公开数据集,直接导入自己的图片数据,下面,就简单写个程序实现批量图片的导入。 import osfrom PIL import Imageimport numpy as np…...

关于unity的组件VerticalLayoutGroup刷新显示不正常的问题
先说明一下我是如何用到,有哪些处理的 用到这个组件基本上都是将列表进行排版操作的,竖着,或者横着,横着用HorizontalLayoutGroup 还有一个和这个组件搭配的组件叫ContentSizeFitter 先说我是怎么发现这个组件不好用的 //本地读取…...

wait 和 notify 这个为什么要在synchronized 代码块中?
一个工作七年的小伙伴,竟然不知道” wait”和“notify”为什么要在 Synchronized 代码块中 。 好吧,如果屏幕前的你也不知道,请在公屏上刷”不知道“。 对于这个问题,我们来看看普通人和高手的回答。 一、问题解析 1. wait 和 n…...
大白话说区块链和通证
1 区块链 简单地说,区块链其实就像是一个不可篡改的分布式数据库,该分布式数据库记录了一系列交易或事件。区块链运行在至少1个以上的节点上,每个节点都有自己的一个分布式数据库,也就是分布式账本。正常情况下,每个节…...
)
Jvm之垃圾收集器(个人见解仅供参考)
问:什么是垃圾收集算法中的分代收集理论? 答:分代收集理论是垃圾收集算法的一种思想,根据对象存活周期的不同将内存分为几块,一般将java堆分为新生代和老年代。这种理论使得我们可以根据各个年代的特点选择合适的垃圾收…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...
