高德地图信息窗体设置
1. 添加默认信息窗体
//构建信息窗体中显示的内容var info = [];info.push(`<div style="height: 36px; line-height: 45px; padding: 0px 20px; white-space:nowrap;">位置:北京</div>`);info.push(`<div style="height: 36px; line-height: 20px; padding: 0px 20px; white-space:nowrap;">联系人:袁磊</div>`);this.infoWindow = new AMap.InfoWindow({content: info.join("") //使用默认信息窗体框样式,显示信息内容});// // getCenter() 获取地图中心点(数组)// this.infoWindow.open(this.aMap, this.aMap.getCenter());// 设置点坐标为窗体坐标;例:[123.40340954550922, 41.7334550336356]this.infoWindow.open(this.aMap, e.data.lnglat);2. 使用自定义窗体(添加窗体)
//构建信息窗体中显示的内容var info = [];info.push(`<div style="height: 36px; line-height: 45px; padding: 0px 20px; white-space:nowrap;">位置:北京</div>`);info.push(`<div style="height: 36px; line-height: 20px; padding: 0px 20px; white-space:nowrap;">联系人:袁磊</div>`);that.infoWindow = new AMap.InfoWindow({isCustom: true, //使用自定义窗体content: `<div style="background: #f00;">jdfghjdfihg</div><div class="close-btn" style="float: right;margin-top: 3px; margin-right: 5px;" onclick="closeInfoWindow()">X</div>`,offset: new AMap.Pixel(16, -45)});// // getCenter() 获取地图中心点(数组)// this.infoWindow.open(this.aMap, this.aMap.getCenter());// 设置点坐标为窗体坐标;例:[123.40340954550922, 41.7334550336356]that.infoWindow.open(that.aMap, e.data.lnglat);3关闭自定义窗体(closeInfoWindow方法也要挂在window)
mounted() {window.closeInfoWindow = () => {this.aMap.clearInfoWindow();};},相关文章:

高德地图信息窗体设置
1. 添加默认信息窗体 //构建信息窗体中显示的内容var info [];info.push(<div style"height: 36px; line-height: 45px; padding: 0px 20px; white-space:nowrap;">位置:北京</div>);info.push(<div style"height: 36px; line-heig…...
isEmpty 和 isBlank 的用法区别,居然一半的人答不上来.....
isEmpty 和 isBlank 的用法区别 isEmpty系列isBank系列 hi!我是沁禹~ 也许你两个都不知道,也许你除了isEmpty/isNotEmpty/isNotBlank/isBlank外,并不知道还有isAnyEmpty/isNoneEmpty/isAnyBlank/isNoneBlank的存在, come on ,让我们一起来探索org.apache…...

数据分析求职-简历准备
简历在整个求职过程中的重要性不言而喻,今天咱们来聊求职过程中简历准备的那些事儿~ 1. 简历究竟有啥用 求职的流程简单说就是:网申->笔试->面试->offer 其中网申环节,简历100%决定了你的通过与否,这个点大家都知道。…...
亚马逊店铺遇到账号申诉模版分享
1.表达诚意,先认错再说:我知道,最近我们在Amazon.com上作为卖家的表现已经低于亚马逊和我们自己的质量标准。 2.清楚分明的格式:我们库存管理的混乱导致了延迟发货,更糟糕的是,物品无法使用。当延迟发货和…...

2023年广东省网络安全A模块(笔记详解)
模块A 基础设施设置与安全加固 一、项目和任务描述: 假定你是某企业的网络安全工程师,对于企业的服务器系统,根据任务要求确保各服务正常运行,并通过综合运用登录和密码策略、流量完整性保护策略、事件监控策略、防火墙策略等多…...
竞赛保研 基于机器视觉的银行卡识别系统 - opencv python
1 前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习的银行卡识别算法设计 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng…...

书摘:C 嵌入式系统设计模式 04
本书的原著为:《Design Patterns for Embedded Systems in C ——An Embedded Software Engineering Toolkit 》,讲解的是嵌入式系统设计模式,是一本不可多得的好书。 本系列描述我对书中内容的理解。 实现类的最简单方法是使用文件作为封装…...

C 练习实例16 - 最大公约数和最小公倍数
题目:输入两个正整数a和b,求其最大公约数和最小公倍数 数学:最大公约数*最小公倍数a*b 例如:a16,b20。最小公倍数80,最大公约数4。80*416*20。 算法:辗转相除法,又称欧几里德算法…...

GAN-概念和应用场景
概念和应用 生成对抗网络 (GAN) 的 18 个令人印象深刻的应用 by 杰森布朗利 on July 12, 2019 in 生成对抗网络110 鸣叫 共享 生成对抗网络 (GAN) 是一种用于生成建模的神经网络架构。 生成式建模涉及使用模型生成可…...

LeetCode(36)有效的数独 ⭐⭐
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图) 注…...

用LCD显示字符‘A‘
#include<reg51.h> //包含单片机寄存器的头文件 #include<intrins.h> //包含_nop_()函数定义的头文件 sbit RSP2^0; //寄存器选择位,将RS位定义为P2.0引脚 sbit RWP2^1; //读写选择位,将RW位定义为P2.1引脚 sbit EP2^2; //使能…...
)
Zookeeper相关问题及答案(2024)
1、ZooKeeper是什么?它的主要用途是什么? ZooKeeper 是一个由 Apache 预先开发和维护的开源服务器,用于协调分布式应用程序。它是一个集中式服务,为分布式应用提供一致性保障,配置管理,命名,同…...

1.大数据概述
目录 概述hadoophadoop 模块hadoop 发行版apache社区版本CDP(CDHHDP)其它云产商框架选择 hadoop 安装 结束 概述 先了解几个常用的网站 apache 官网hadoop 官网hadoop githubhttps://github.com/apache/xxx [https://github.com/apache/spark (example)] hadoop hadoop 模块…...

NGUI基础-Widget
目录 Widget是什么 Widget组件包含的属性 Pivot Depth Size snap Aspect Free Based on Width Based on Height Widget是什么 在Unity UI系统中,"Widget"是指UI元素的基类,它为UI元素提供了位置、大小和锚点等基本属性。通过使用&qu…...

SpringBoot集成沙箱支付
前言 支付宝沙箱支付(Alipay Sandbox Payment)是支付宝提供的一个模拟支付环境,用于开发和测试支付宝支付功能的开发者工具。在真实的支付宝环境中进行支付开发和测试可能涉及真实资金和真实用户账户,而沙箱环境则提供了一个安全…...
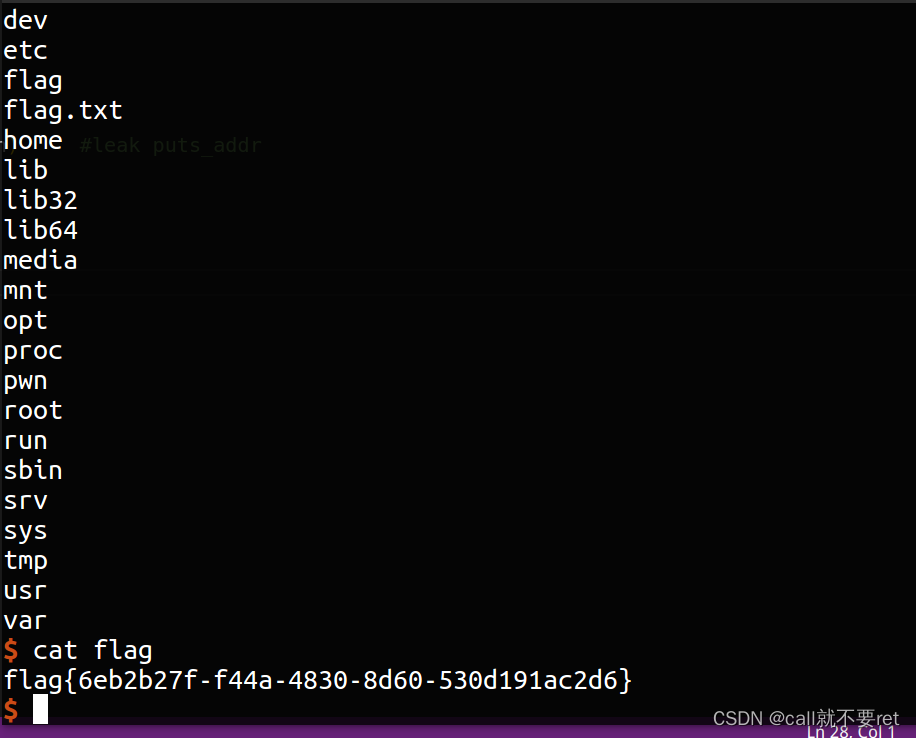
BUUCTF--gyctf_2020_borrowstack1
这是一题栈迁移的题目,先看看保护: 黑盒测试: 用户可输入两次内容,接着看看IDA中具体程序流程: 我们看到溢出内容只有0x10的空间给我们布局,这显然是不足以我们布置rop的。因此肯定就是栈迁移了。迁到什么地…...

图像分割-Grabcut法(C#)
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 本文的VB版本请访问:图像分割-Grabcut法-CSDN博客 GrabCut是一种基于图像分割的技术,它可以用于将图像中的…...

C# WPF上位机开发(Web API联调)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 很多时候,客户需要开发的不仅仅是一个上位机系统,它还有其他很多配套的系统或设备,比如物流小车、立库、数字孪…...

c语言:用结构体求平均分|练习题
一、题目 用c语言的结构体,求4位学生成绩的平均分 如图: 二、代码截图【带注释】 三、源代码【带注释】 #include <stdio.h> float aver();//声明平均分函数 void printScore();//声明打印函数 //设置结构体, struct student { …...

echarts 仪表盘进度条 相关配置
option {series: [{type: gauge,min: 0,//最大值max: 100, //最小值startAngle: 200,//仪表盘起始角度。圆心 正右手侧为0度,正上方为90度,正左手侧为180度。endAngle: -20,//仪表盘结束角度splitNumber: 100, //仪表盘刻度的分割段数itemStyle: {color…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
