[C/C++]排序算法 快速排序 (递归与非递归)
目录
🚩概念:
🚩实现:
⚡1.hoare
⚡2.挖坑法
⚡3.双指针法
🚩快速排序递归实现
🚩快速排序非递归实现
🚩概念:
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据比另一部分的所有数据要小,再按这种方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,使整个数据变成有序序列。
🌟排序过程:
1.在数组中确定一个关键值
2.将小于关键值的数排到其左边,将大于关键值的数排到其右边,此时关键数在数组中的位置就排好了
3.在左边的数据和右边的数据分别找一个关键值,通过排序使小于关键值的数排到其左边,大于关键值的数排到其右边...
4.重复上述操作,可以通过递归与非递归实现
快速排序的关键是写好步骤二的单趟排序,实现这个功能有三种版本
- hoare
- 挖坑法
- 双指针法
🚩实现:
⚡1.hoare
将数组第一个元素定位关键值,定义begin和end指针,先让end从后往前找到比关键值小的数,begin从前往后找比关键值大的数,然后交换两数,直到 begin==end,再让关键值和begin所指的元素交换,最后返回关键值所在位置,便于后续进行递归或非递归操作(一定要先从后往前找小,原因下文解释)
动态展示:

void swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//hoare
int PartSort1(int* a, int begin, int end)
{int left = begin, right = end;int keyi = begin;while (left < right){//右边找小while (left < right && a[right] >= a[keyi]){right--;}//左边找大while (left < right && a[left] < a[keyi]){left++;}swap(&a[left], &a[right]);}swap(&a[left], &a[keyi]);return left;
}⚡2.挖坑法
首先将关键值定为数组第一个元素,并将坑位定为begin,先让end从后往前找到比关键值小的数,将这个数放到坑位,并更新坑位,再让begin从前往后找比关键值大的数,将这个数放到坑位,并更新坑位,直到 begin==end,再让关键值和坑位的元素交换,最后返回关键值所在位置
//挖坑法
int PartSort2(int* a, int begin, int end)
{int mid = GetMid(a, begin, end);swap(&a[begin], &a[mid]);int key = a[begin];int hole = begin;while (begin < end){//右边找小,填入坑内,更新坑位while (begin<end && a[end]>=key){--end;}a[hole] = a[end];hole = end;//左边找大,填入坑内,更新坑位while (begin<end && a[begin]<=key){++begin;}a[hole] = a[begin];hole = begin;}a[hole] = key;return hole;
}⚡3.双指针法
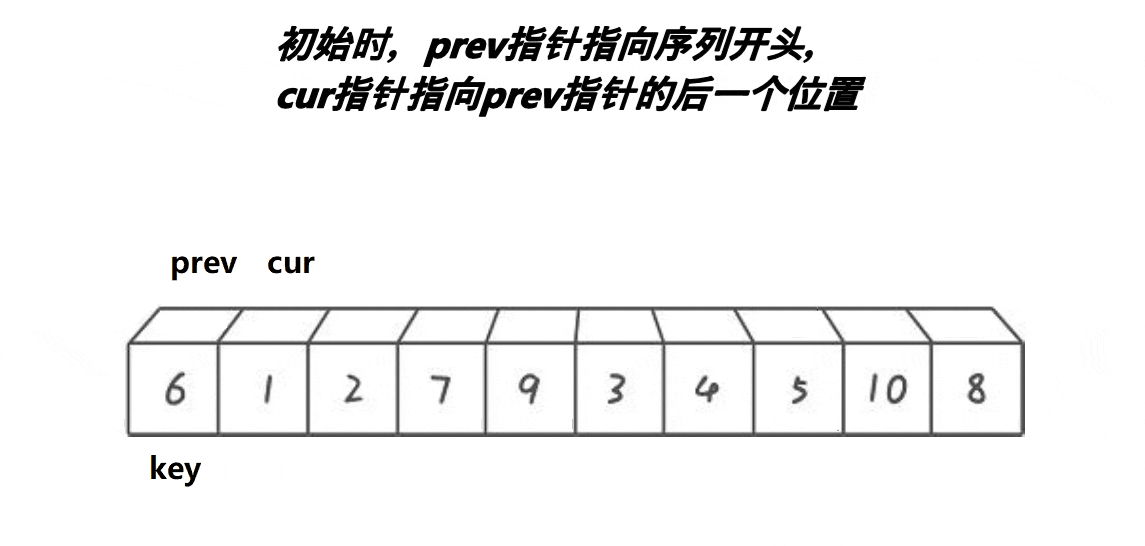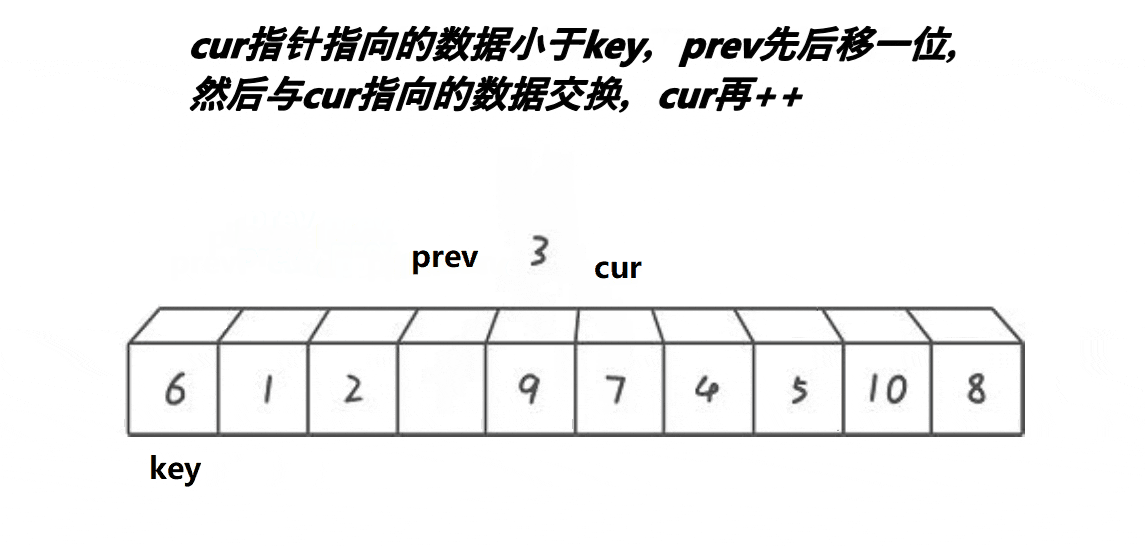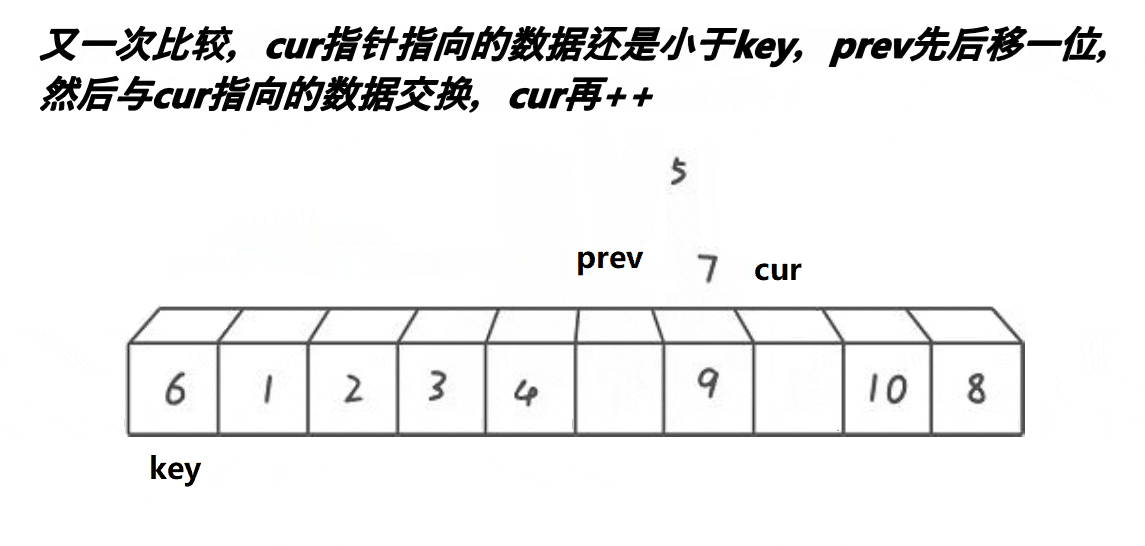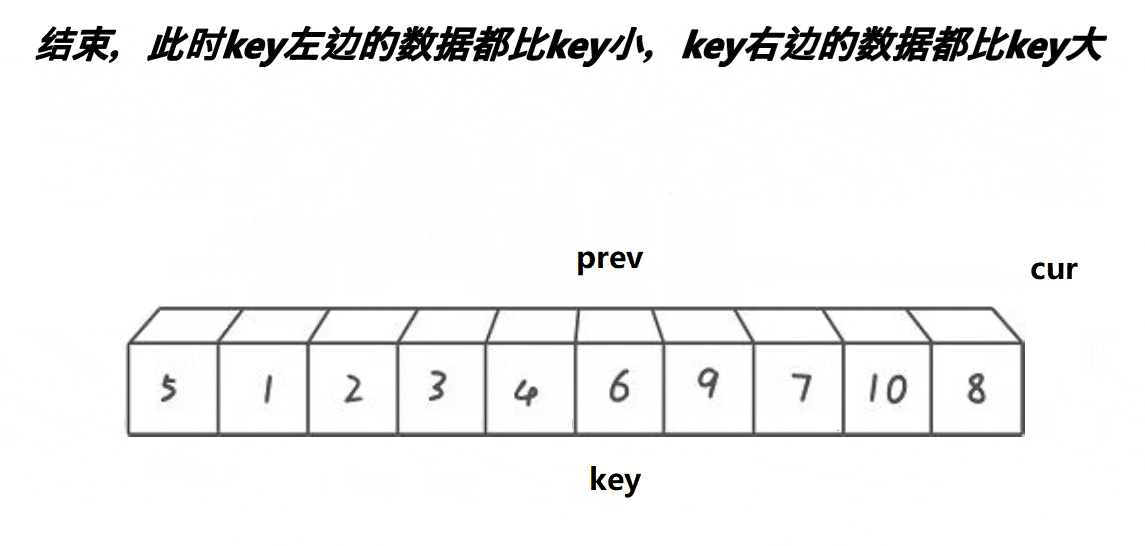
将数组第一个元素定为关键值,定义两个指针prev和cur,先让prev指向数组的第一个元素,cur指向prev的下一个元素,cur的作用是找比关键值小的元素,若cur所指元素不小于关键值则cur++,直到cur所值元素小于关键值,此时,prev和cur之间的元素都是大于关键值的元素,若prev+1不是cur的话就可以让prev++所指元素与cur所指元素交换了,直到cur指向数组的最后一个元素
这里可能会有人出现问题:
1.为什么要判断 prev++!=cur
[解释]:如果prev+1为cur的话,那交换prev++和cur所指元素那就是一个元素之间的交换了,没有意义
2.为什么要交换prev++所指元素
[解释]:因为prev和cur之间的元素都为大于关键值的元素,prev++就可以让prev指向大于关键值的元素,而cur所指的是小于关键值的元素,这样一交换小的数就去前面了,大的数就去后面了
//双指针法
int PartSort3(int* a, int begin, int end)
{int mid = GetMid(a, begin, end);swap(&a[begin], &a[mid]);int key = begin;int prev = begin;int cur = prev + 1;while (cur <= end){if (a[cur] < a[key] && ++prev != cur){swap(&a[prev], &a[cur]);}cur++;}swap(&a[prev], &a[key]);return prev;
}🚩快速排序递归实现
⛲小优化:
上述三个方法都是快速排序的单趟排序,但是上述排序还有一个小缺陷,因为三个方法都是固定第一个元素为关键值的,如果数组为有序的,那么从后往前找小就要遍历整个数组,效率会很小,所以通常会再写一个找中间值的函数:在数组开头结尾和中间三个数中找出一个大小在中间的数,并让这个数和数组第一个数交换,这样就会减少上述情况的发生
int GetMid(int* a, int begin, int end)
{int mid = (begin + end) / 2;if (a[begin] > a[mid]){if (a[mid] > a[end])return mid;else if (a[end] > a[begin])return end;elsereturn begin;}else{if (a[begin] > a[end])return begin;else if (a[end] > a[mid])return mid;elsereturn end;}
}void swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//hoare
int PartSort1(int* a, int begin, int end)
{int mid = GetMid(a, begin, end);swap(&a[begin], &a[mid]);int left = begin, right = end;int keyi = begin;while (left < right){//右边找小while (left < right && a[right] >= a[keyi]){right--;}//左边找大while (left < right && a[left] < a[keyi]){left++;}swap(&a[left], &a[right]);}swap(&a[left], &a[keyi]);return left;
}//挖坑法
int PartSort2(int* a, int begin, int end)
{int mid = GetMid(a, begin, end);swap(&a[begin], &a[mid]);int key = a[begin];int hole = begin;while (begin < end){//右边找小,填入坑内,更新坑位while (begin<end && a[end]>=key){--end;}a[hole] = a[end];hole = end;//左边找大,填入坑内,更新坑位while (begin<end && a[begin]<=key){++begin;}a[hole] = a[begin];hole = begin;}a[hole] = key;return hole;
}
//双指针法
int PartSort3(int* a, int begin, int end)
{int mid = GetMid(a, begin, end);swap(&a[begin], &a[mid]);int key = begin;int prev = begin;int cur = prev + 1;while (cur <= end){if (a[cur] < a[key] && ++prev != cur){swap(&a[prev], &a[cur]);}cur++;}swap(&a[prev], &a[key]);return prev;
}
void QuickSort(int* a, int begin,int end)
{if (begin >= end)return;//三种方法任选其一即可int keyi = PartSort3(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}
补充:
为什么开始一定要右边找小,并且为什么left和right相遇那个点一定小于关键值呢?
[解释]:
L遇到R有两种情况
- R遇到L: R从右往左找小,一直没找到小,直到遇到L,而L的点的值小于关键值(因为此时L的值是和上一轮R找的小的值)
- L遇到R:R先从右找小,找到小停下来,L从左往右找打大没有找到遇到R,相遇点的值小于关键值
🚩快速排序非递归实现
快速排序的递归实现,无非就是通过调用函数对数组的不同区间进行排序,而非递归我们也可以用栈实现,不是递归胜似递归.
实现思路:
1.创建一个栈,将数组的右边界下标和左边界下标依次入栈
2.循环弹出数组的左右边界下标,并对该区间进行单趟排序,确定关键值的下标,分为左右两个区间
3.若左区间元素个数大于一个,将左区间右边界下标和左边界下标依次入栈,右区间同理
4.重复操作步骤2 3直到栈为空
例如待排序数组为:

第一步:将右边界下标和左边界下标7和0入栈

第二步:将边界值弹出,将0给到begin,7给到end,进行单趟排序(单趟排序采用挖坑法)
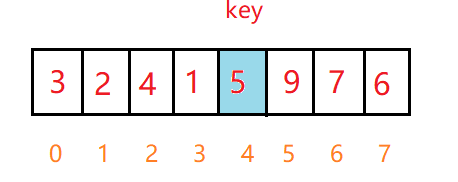
排序完后,key将数组分为了左右两个区间,让右区间边界7和5入栈,左边界3和0入栈

第三步:取出0 3并对此区间单趟排序

此时,关键值又把区间分为了两个区间,右区间只有一个值,没必要入栈排序,只需要将左区间边界1 0入栈
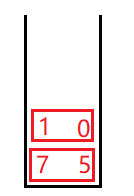
再弹出0 1,对此区间单趟排序,此时左区间无元素,有区间只有一个元素,这样数组左边就全部排序完成了,再次出栈的话就该排序5和7的区间了,和左边类似
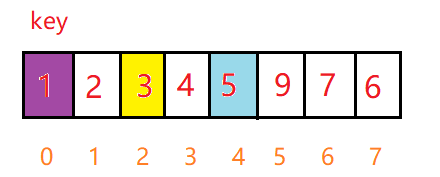
void QuickSortNonR(int* a, int begin, int end)
{ST s;STInit(&s);STPush(&s,end);STPush(&s,begin);while (!STEmpty(&s)){int left = STTop(&s);STPop(&s);int right = STTop(&s);STPop(&s);int key = PartSort1(a, left, right);if (left < key - 1){STPush(&s, key - 1);STPush(&s, left);}if (right > key + 1){STPush(&s, right);STPush(&s, key+1);}}STDestroy(&s);
}相关文章:

[C/C++]排序算法 快速排序 (递归与非递归)
目录 🚩概念: 🚩实现: ⚡1.hoare ⚡2.挖坑法 ⚡3.双指针法 🚩快速排序递归实现 🚩快速排序非递归实现 🚩概念: 通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据比另一部分的所有…...

『年度总结』逐梦编程之始:我的2023学习回顾与展望
目录 前言 我与Python 我与C语言 第一篇正式博客: 第二篇正式博客(扫雷): 指针学习笔记: C语言学习笔记: 我与数据结构: yuan 这篇博客,我将回顾2023年编程之旅的起点,同时展…...
MyBatis学习二:Mapper代理开发、配置文件完成增删改查、注解开发
前言 公司要求没办法,前端也要了解一下后端知识,这里记录一下自己的学习 学习教程:黑马mybatis教程全套视频教程,2天Mybatis框架从入门到精通 文档: https://mybatis.net.cn/index.html Mapper代理开发 目的 解决…...
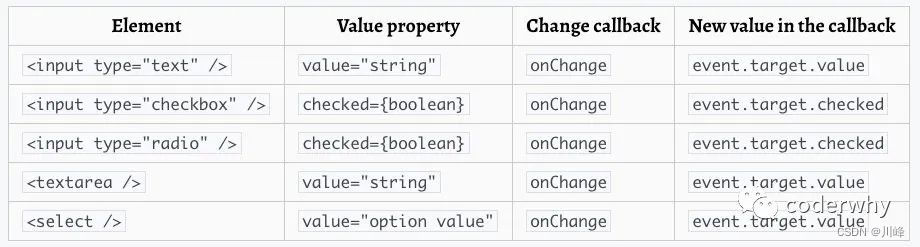
【React系列】受控非受控组件
本文来自#React系列教程:https://mp.weixin.qq.com/mp/appmsgalbum?__bizMzg5MDAzNzkwNA&actiongetalbum&album_id1566025152667107329) 一. refs 的使用 在React的开发模式中,通常情况下不需要、也不建议直接操作DOM原生,但是某些…...
:2D直方图)
OpenCV-Python(22):2D直方图
目标 了解图像的2D直方图绘制2D直方图 介绍 在前面的部分我们介绍了如何绘制一维直方图,之所以称为一维,是因为我们只考虑了图像的一个特征:灰度值。但是在2D 直方图中我们就需要考虑两个图像特征。对于彩色图像的直方图通常情况下我们需要…...

Kubernetes 100个常用命令
本文简单总结关于使用 Kubectl 进行 Kubernetes 诊断的指南。列出了 100 个 Kubectl 命令,这些命令对于诊断 Kubernetes 集群中的问题非常有用。这些问题包括但不限于: 集群信息 Pod 诊断 服务诊断 部署诊断 网络诊断 持久卷和持久卷声明诊断 资源…...

labuladong日常刷题-差分数组 | LeetCode 1109航班预定统计 | 花式遍历 151反转字符串里的单词
差分数组–前缀和数组的升级 LeetCode 1109 航班预定统计 2024.1.1 题目链接labuladong讲解[链接] class Solution { public:vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {//构建航班人数数组,数组大小为n,初…...
HbuilderX中的git的使用
原文链接https://blog.csdn.net/Aom_yt/article/details/119924356...

LeetCode每日一题 | 1944. 队列中可以看到的人数
文章目录 队列中可以看到的人数题目描述问题分析程序代码(Golang 版本) 队列中可以看到的人数 题目描述 原题链接 有 n 个人排成一个队列,从左到右 编号为 0 到 n - 1 。给你以一个整数数组 heights ,每个整数 互不相同ÿ…...

React16源码: JSX2JS及React.createElement源码实现
JSX 到 Javascript 的转换 React中的 JSX 类似于 Vue中的template模板文件,Vue是基于编译时将template模板转换成render函数在React中,JSX是类似于html和javascript混编的语法,而javascript是真的javascript, html并非真的html它的可阅读性可…...

整理composer安装版本的python脚本
整理composer安装版本的python脚本 脚本实现的功能是去除composer安装命令后的版本号 def remove_version_numbers(commands):"""Remove version numbers from composer require commands.Args:commands (list of str): List of composer require commands.Retu…...
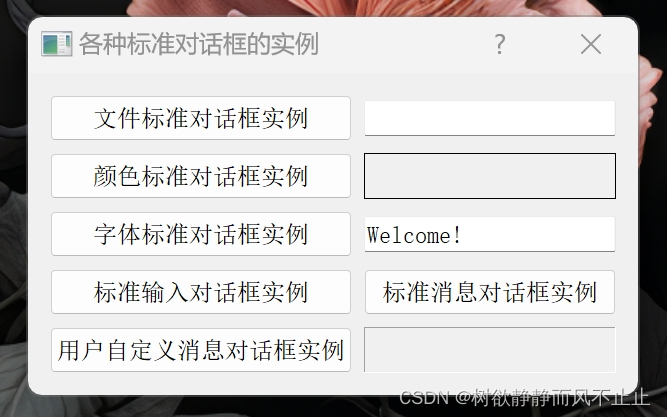
十、基本对话框大集合(Qt5 GUI系列)
目录 一、设计需求 二、实现代码 三、代码解析 四、总结 一、设计需求 Qt提供了很多标准的对话框。例如标准文件对话框(QFileDialog)、标准颜色对话框(QColorDialog)、标准字体对话框 (QFontDialog)、标准输入对话框 (QInputDialog) 及消息对话框 (QMessageBox)。本文展示各…...

大A又跌了
才开盘几天,又开始下跌了。生活更加苦难。期待高深算法。...
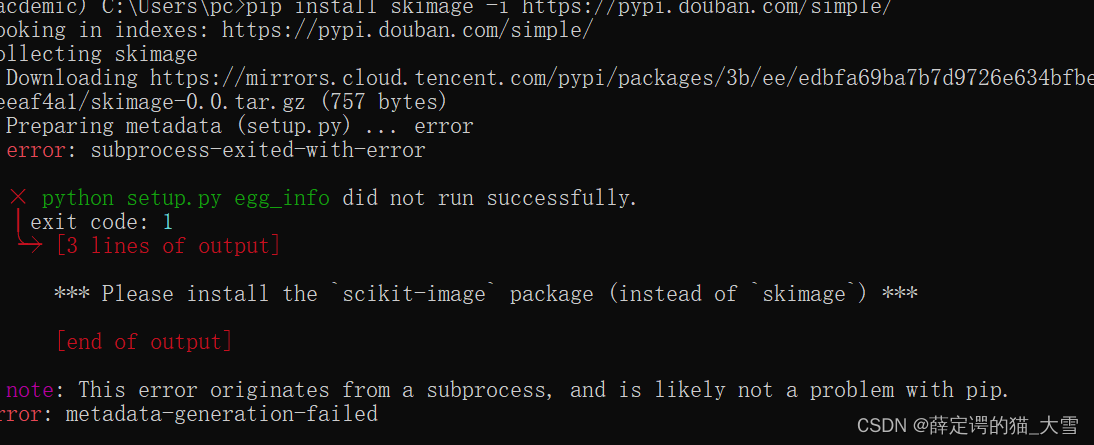
This error originates from a subprocess, and is likely not a problem with pip
我遇这个问题是的原因是包名错误 注意检查包名...

数据库基础知识1
关系模型的程序员不需熟悉数据库的存取路径 在3层模式结构中,___I___是数据库的核心和关键,___Ⅱ___通常是模式的子集,数据库模式的描述提供给用户,____Ⅲ__的描述存储在硬盘上。Ⅰ.模式Ⅱ. 外模式Ⅲ. 内模式 数据库中,数据的物理独立性是指用户的应用程序与存储在磁盘上数据库…...
【GO语言卵细胞级别教程】01.GO基础知识
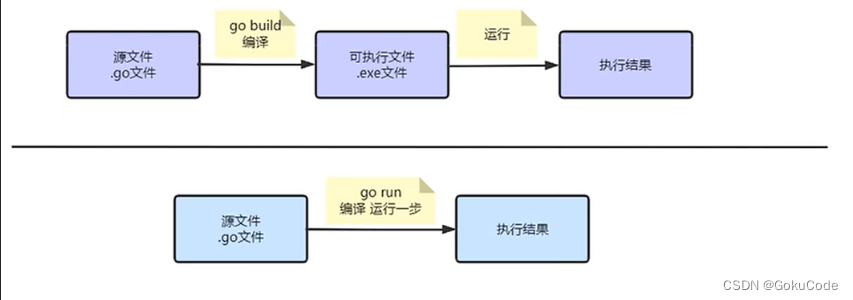
01.GO基础知识 目录 01.GO基础知识1.GO语言的发展历程2.发展历程3.Windowns安装4.VSCode配置5.基础语法5.1 第一段代码5.2 GO执行的流程5.3 语法规则5.4 代码风格5.5 学习网址 1.GO语言的发展历程 Go语言是谷歌公司于2007年开始开发的一种编程语言,由Robert Griese…...
】按身高和体重排排队(排序题-JavaPythonC++JS实现))
215.【2023年华为OD机试真题(C卷)】按身高和体重排排队(排序题-JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-按身高和体重排排队二.解题思路三.题解代码Pyt…...
)
虚函数(C++)
四、多态4.1 虚函数 四、多态 多态性是面向对象程序设计语言的又一重要特征,多态(polymorphism)通俗的讲,就是用一个相同的名字定义许多不同的函数,这些函数可以针对不同数据类型实现相同或类似的功能,即所…...

力扣25题: K 个一组翻转链表
【题目链接】力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台,解题代码如下: class Solution {public ListNode reverseKGroup(ListNode head, int k) {ListNode curNode head;ListNode groupHead, groupTail head, lastGrou…...
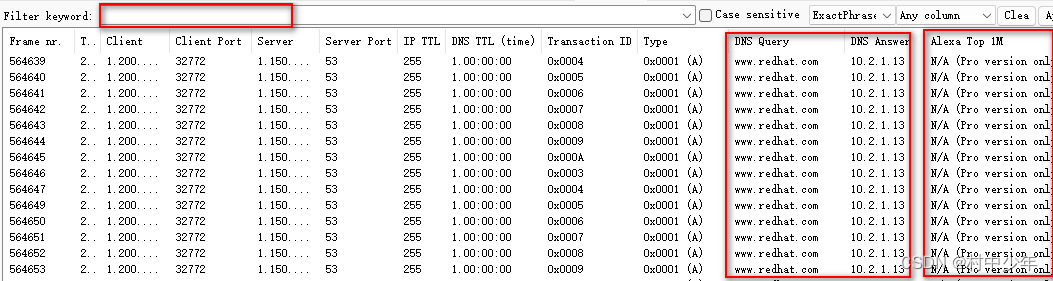
网络安全应急响应工具之-流量安全取证NetworkMiner
在前面的一些文章中,用了很多的章节介绍流量分析和捕获工具wireshark。Wireshark是一款通用的网络协议分析工具,非常强大,关于wireshark的更多介绍,请关注专栏,wireshark从入门到精通。本文将介绍一个专注于网络流量取…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
