LeetCode74二分搜索优化:二维矩阵中的高效查找策略
题目描述
力扣地址
给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
示例 1:
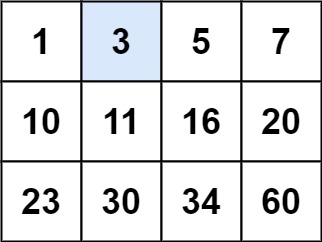
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 输出:true
示例 2:
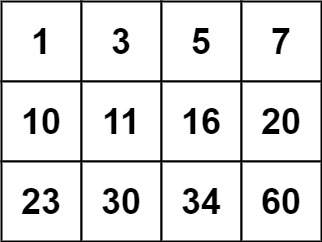
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
以右上或左下为起点进行搜索
class Solution {public boolean searchMatrix(int[][] matrix, int target) {int row = matrix.length;int col = matrix[0].length;int i = 0;int j = col-1;while(i>-1 && i<row && j>-1 && j<col){if(matrix[i][j] < target){i++;}else if(matrix[i][j] > target){j--;}else{return true;}}return false;}
}这种解法效率不高需要用二分来优化,这道题目描述的矩阵具有两个关键属性:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
由于这两个属性,虽然矩阵是二维的,但它可以被视为一个一维的有序数组。具体来说,如果我们将这个矩阵“展开”成一个一维数组,这个数组将是有序的。这使得我们可以在这个虚拟的一维数组上应用二分查找算法。
class Solution {public boolean searchMatrix(int[][] matrix, int target) {int row = matrix.length;int col = matrix[0].length;int left = 0;int right = row * col - 1;while (left <= right) {int midIndex = left + (right - left) / 2;int midValue = matrix[midIndex / col][midIndex % col];if (midValue == target) {return true;} else if (midValue < target) {left = midIndex + 1;} else {right = midIndex - 1;}}return false;}
}LeetCode378之有序矩阵中第 K 小的元素(相关话题:优先队列,二分)
这道题不具备每行的第一个整数大于前一行的最后一个整数这个属性所以不能直接把二维矩阵转化为一维数据进行二分。而是直接对矩阵里的最大值和最小值进行二分。
相关文章
LeetCode之团灭旋转数组(相关话题:减治,二分,分治)_target的最小数的下标-CSDN博客
LeetCode287之寻找重复数(相关话题:二分查找,快慢指针)-CSDN博客
LeetCode287之寻找重复数(相关话题:位运算,抽屉原理)_442. 数组中重复的数据 leetcode python-CSDN博客
算法模板(一)(相关话题:二分搜索)_if (left >= nums.length || nums[left] != target) r-CSDN博客
LeetCode378之有序矩阵中第 K 小的元素(相关话题:优先队列,二分)_java给你一个 n x n 矩阵 matrix ,其中每行和每列元素均按升序排序,找到矩阵中第-CSDN博客
LeetCode1095.之山脉数组中查找目标值(相关话题:多重二分)-CSDN博客
相关文章:

LeetCode74二分搜索优化:二维矩阵中的高效查找策略
题目描述 力扣地址 给你一个满足下述两条属性的 m x n 整数矩阵: 每行中的整数从左到右按非严格递增顺序排列。每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则&…...

三极管组成的光控开关电路原理图
什么是光控开关 光控开关/光控时控器采用先进的嵌入式微型计算机控制技术,融光控功能和普通时控器两大功能为一体的多功能高级时控器(时控开关),根据节能需要可以将光控探头(功能)与时控功能同时启用&…...
系统列)
【PostgreSQL】从零开始:(四十二)系统列
PostgreSQL 中的系统列 PostgreSQL 中的系统列是一组特殊的列,用于存储关于表和视图的元数据信息。这些列是由 PostgreSQL 数据库自动创建和维护的,并且不能直接修改或删除。 每个表都有多个系统列,这些列由系统隐式定义。因此,…...

快速、准确地检测和分类病毒序列分析工具 ViralCC的介绍和详细使用方法, 附带应用脚本
介绍 viralcc是一个基因组病毒分析工具,可以用于快速、准确地检测和分类病毒序列。 github:dyxstat/ViralCC: ViralCC: leveraging metagenomic proximity-ligation to retrieve complete viral genomes (github.com) Instruction of reproducing resul…...

DNs服务学习笔记
DNS:域名系统(英文:Domain Name System)是一个域名系统,是万维网上作为域名和IP地址相互映射的一个分布式数据库,能够使用户更方便的访问互联网,而不用去记住能够被机器直接读取的IP数串。类似于生活中的11…...

获取线程池中任务执行数量
获取线程池中任务执行数量 通过线程池进行任务处理,有时我们需要知道线程池中任务的执行状态。通过ThreadPoolExecutor的相关API实时获取线程数量,排队任务数量,执行完成线程数量等信息。 实例 private static ExecutorService es new Thr…...

RK3566 Android 11平台上适配YT8512C 100M PHY
RK3566代码之前适配的1000M IC RTL8211F , 现在需要在之前的基础上修改PHY IC 为裕泰的YT8512C ----------------------------------------------------------------------//将1000M 的配置关掉,改为100M 配置,查看RK3566 资料关于以太网的配置即可知道如何修改 #if…...
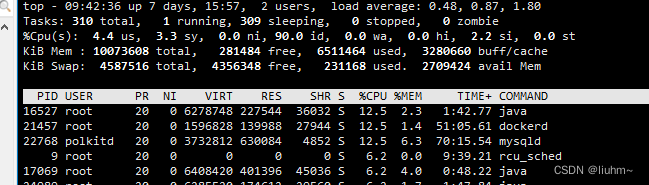
docker 部署haproxy cpu占用特别高
在部署mysql 主主高可用时,使用haproxy进行负载,在服务部使用的情况下发现服务器cpu占比高,负载也高,因此急需解决这个问题。 1.解决前现状 1.1 部署配置文件 cat > haproxy.cfg << EOF globalmaxconn 4000nbthrea…...
Oracle导出CSV文件
利用spool spool基本格式: spool 路径文件名 select col1||,||col2||,||col3||,||col4 from tablename; spool off spool常用的设置: set colsep ; //域输出分隔符 set echo off; //显示start启动的脚本中的每个sql命令,缺…...

图像分割实战-系列教程12:deeplab系列算法概述
🍁🍁🍁图像分割实战-系列教程 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在Pycharm中进行 本篇文章配套的代码资源已经上传 1、deeplab概述 图像分割中的传统做法:为了增大感受野,通常都会选择pooling…...

数据库02-07 存储
计算机存储系统: 02.磁道存储...
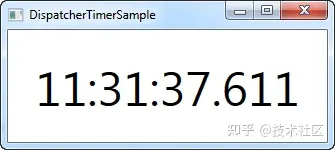
WPF 入门教程DispatcherTimer计时器
https://www.zhihu.com/tardis/bd/art/430630047?source_id1001 在 WinForms 中,有一个名为 Timer 的控件,它可以在给定的时间间隔内重复执行一个操作。WPF 也有这种可能性,但我们有DispatcherTimer控件,而不是不可见的控件。它几…...
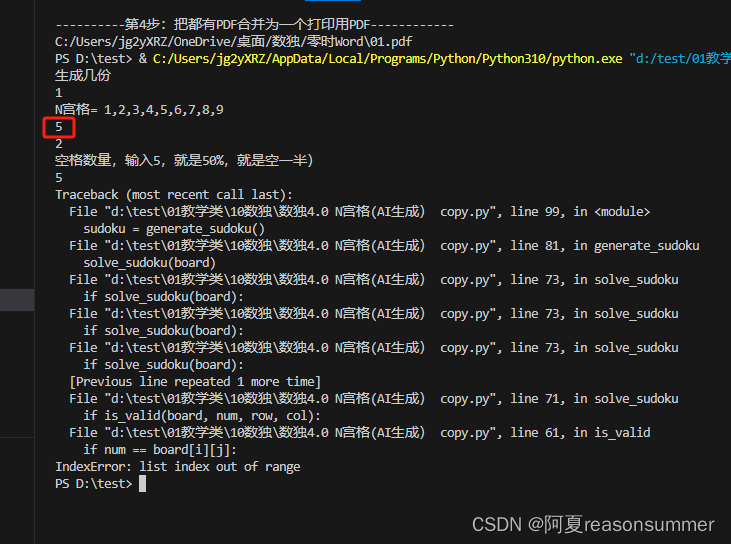
【教学类-43-04】20231229 N宫格数独4.0(n=2,4,6,8) (ChatGPT AI对话大师生成 回溯算法)
作品展示: 背景需求: 幼儿表示自己适合做5宫格 第一次AI生成九宫格数独python代码 【教学类-43-03】20231229 N宫格数独3.0(n1、2、3、4、6、8、9) (ChatGPT AI对话大师生成)-CSDN博客文章浏览阅读162次&…...

WPF美化ItemsControl1:不同颜色间隔
首先我们有的是一个绑定好数据的ItemsControl <ItemsControl ItemsSource"{Binding Starts}"> </ItemsControl> 运行后呢是朴素的将数据竖着排列 如果想要数据之间有间距,可以使用数据模板,将数据放到TextBlock中显示࿰…...
查看进程对应的路径查看端口号对应的进程ubuntu 安装ssh共享WiFi设置MyBatis 使用map类型作为参数,复杂查询(导出数据)
Linux 查询当前进程所在的路径 top 命令查询相应的进程号pid ps -ef |grep 进程名 lsof -I:端口号 netstat -anp|grep 端口号 cd /proc/进程id cwd 进程运行目录 exe 执行程序的绝对路径 cmdline 程序运行时输入的命令行命令 environ 记录了进程运行时的环境变量 fd 目录下是进…...

医院信息系统集成平台—安全保障体系
隐私保护措施 隐私保护及信息安全是医院信息平台所要重点解决的问题,应从患者同意,匿名化服务,依据病种、角色等多维度授权,关键信息(字段级、记录级、文件级)加密存储等方面展开。电子病历等医疗数据进行调阅时,包括强身份认证需求、角色授权需求、责任认…...

【信息论与编码】习题-填空题
目录 填空题1.克劳夫特不等式是判断( )的充要条件。2.无失真信源编码的中心任务是编码后的信息率压缩接近到()限失真压缩中心任务是在给定的失真度条件下,信息率压缩接近到( )。3.常用的检纠错方…...
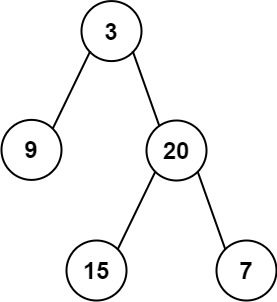
二叉树的层序遍历经典问题(算法村第六关白银挑战)
基本的层序遍历与变换 二叉树的层序遍历 102. 二叉树的层序遍历 - 力扣(LeetCode) 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 示例 1: 输入…...

信息学奥赛一本通:装箱问题
题目链接:http://ybt.ssoier.cn:8088/problem_show.php?pid1917 题目 1917:【01NOIP普及组】装箱问题 时间限制: 1000 ms 内存限制: 65536 KB 提交数: 4117 通过数: 2443 【题目描述】 有一个箱子容量为V�(正整数,…...
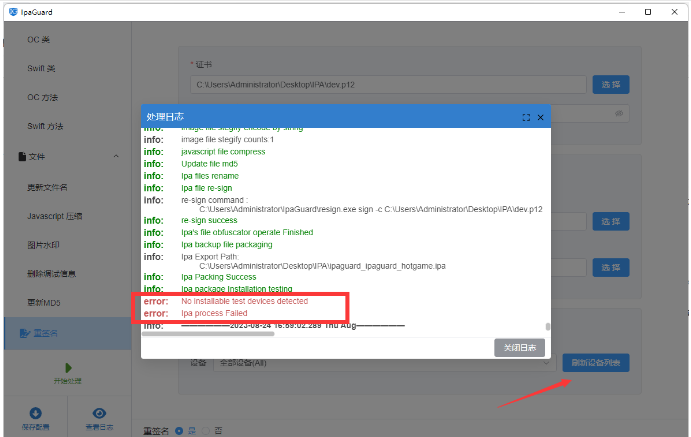
ReactNative 常见问题及处理办法(加固混淆)
ReactNative 常见问题及处理办法(加固混淆) 文章目录 摘要引言正文ScrollView内无法滑动RN热更新中的文件引用问题RN中获取高度的技巧RN强制横屏UI适配问题低版本RN(0.63以下)适配iOS14图片无法显示问题RN清理缓存RN navigation参…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...
