当前位置： 首页 > news >正文

Jenkins集成部署java项目

news 2026/1/13 14:03:31

文章目录

      • Jenkins简介
      • 安装

Jenkins简介

Jenkins能实时监控集成中存在的错误，提供详细的日志文件和提醒功能，还能用图表的形式形象的展示项目构建的趋势和稳定性。
官网
在这里插入图片描述

安装

在官网下载windows版本的Jenkins
在这里插入图片描述
但是我点击这里浏览器没有反应，所以我去下载旧版本。
在这里插入图片描述.在这里插入图片描述
如果版本过低可能会导致插件无法下载的错误

下载完成后，在控制台启动Jenkins
使用命令 java -jar jenkins.war
在这里插入图片描述
在这里插入图片描述

启动成功后登录 localhost:8080 进入页面
在这里插入图片描述
插件安装完成后，用admin账户登录
在这里插入图片描述

相关文章：

Jenkins集成部署java项目

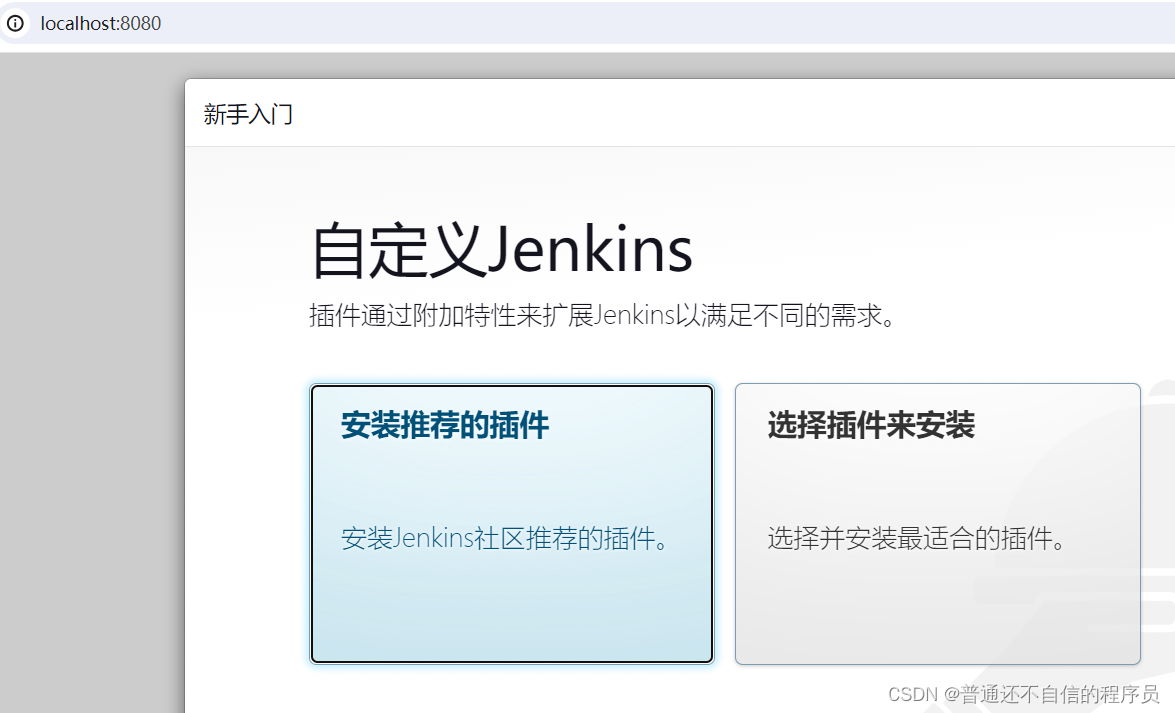
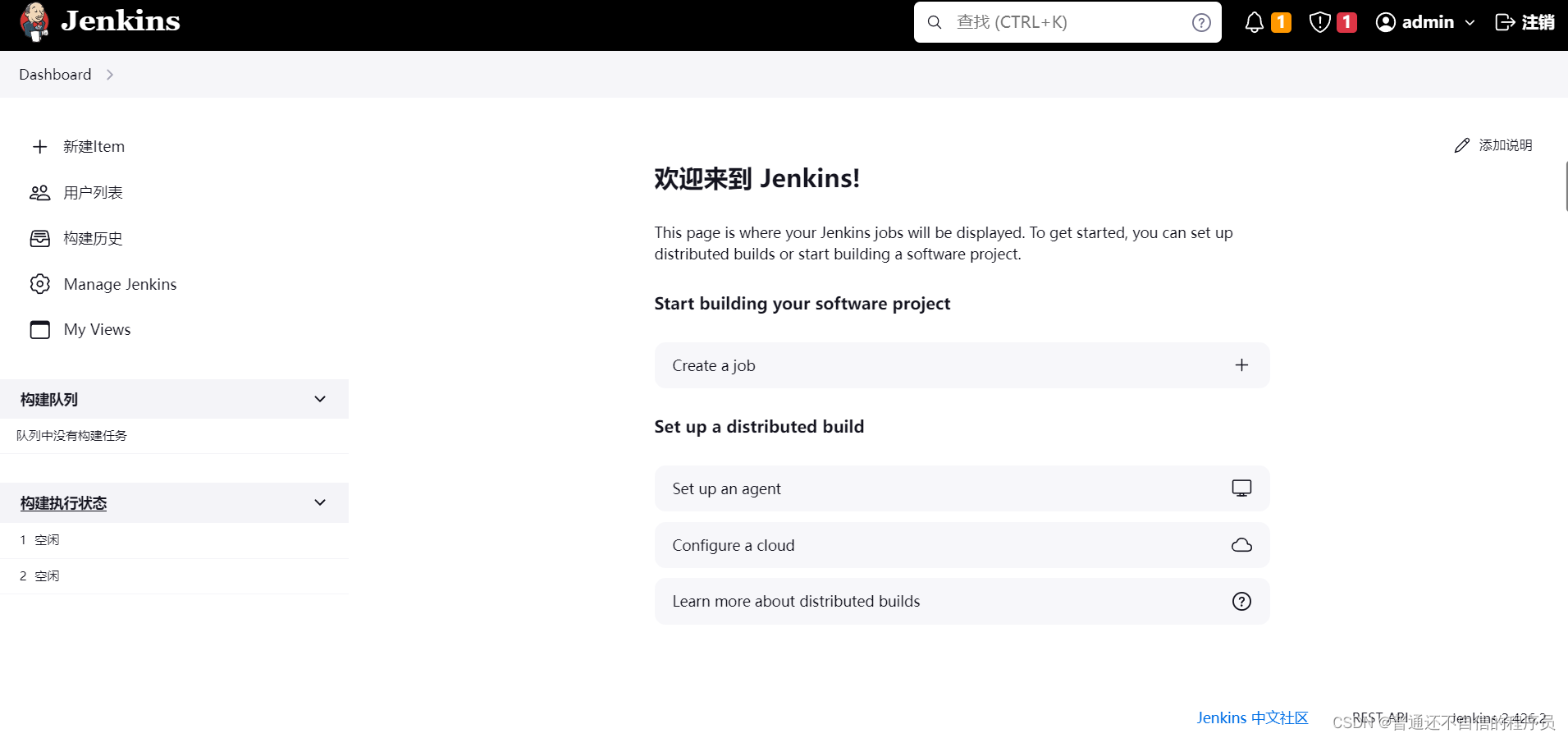
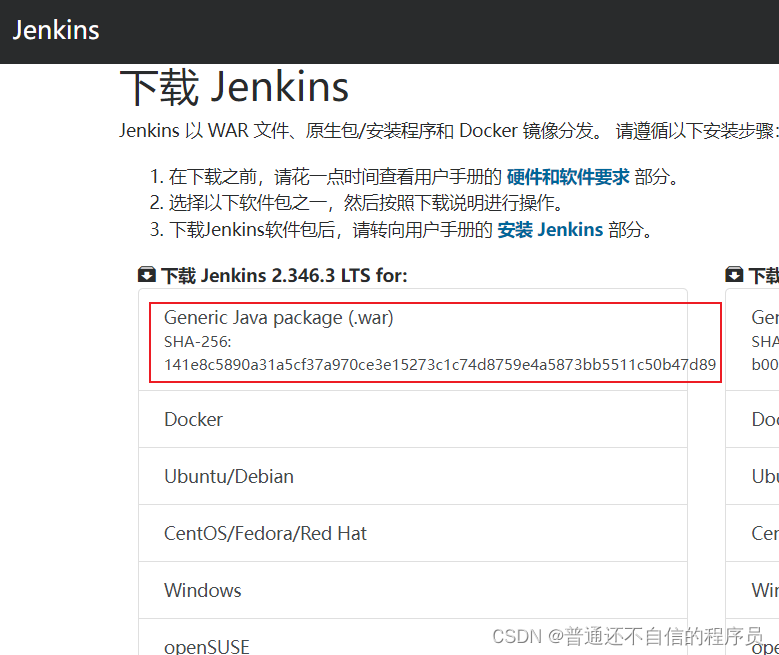
文章目录 Jenkins简介安装 Jenkins简介 Jenkins能实时监控集成中存在的错误，提供详细的日志文件和提醒功能，还能用图表的形式形象的展示项目构建的趋势和稳定性。 官网 安装 在官网下载windows版本的Jenkins 但是我点击这里浏览器没有反应&#xff0…...

编程日记 2024/1/6 7:38:13

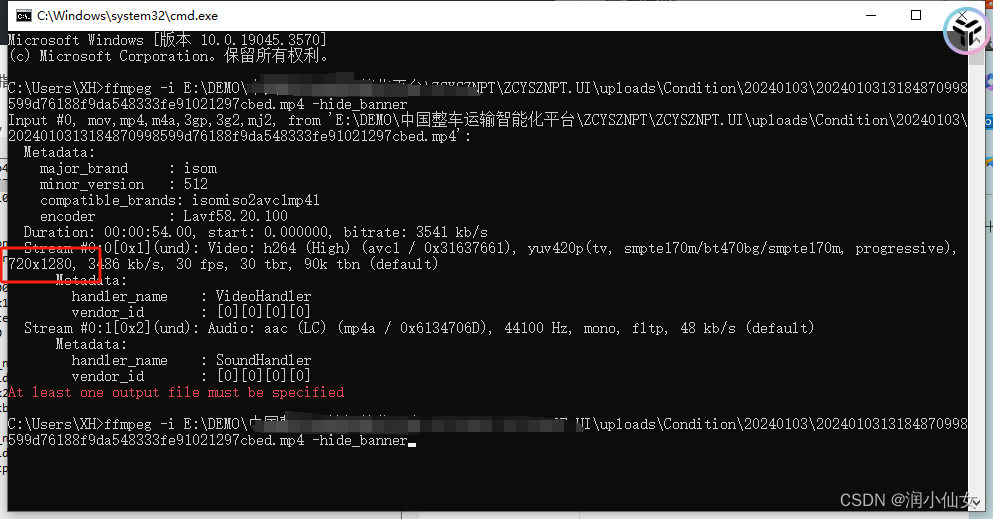
FFmpeg之——获取上传视频的尺寸（长、宽）

获取上传视频的尺寸： 获取视频尺寸通常需要借助第三方库FFmpeg。 首先，确保你的系统中已安装了FFmpeg，并且FFmpeg的可执行文件路径已经添加到你的系统环境变量中。 1.官网下载ffmpeg 进入 链接: ffmpeg官网 网址，点击下载wind…...

编程日记 2024/1/6 7:36:11

Ajax学习

文章目录 AjaxAjax 是什么Ajax 经典应用场景Ajax 原理示意图ajax的异步请求的方法ajax的逻辑：应用实例-验证用户名是否存在思路框架图：需求分析: 到数据库去验证用户名是否可用思路框架图大功告成：使用JQuery-Ajax实现上面相同的需求：Ajax Ajax 是什么 AJAX 即"Async…...

编程日记 2024/1/6 7:29:06

排序算法——关于快速排序的详解

目录 1.基本思想 2.基本原理 2.1划分思想 2.2排序过程 （1）选择基准值 （2）分割过程（Partition） （3）递归排序 （4）合并过程 2.3具体实例 2.4实现代码 2.5关键要…...

编程日记 2024/1/6 7:28:05

序言：《未来已来》

尊敬的读者， 你是否曾经在面对冗长的报告、繁琐的工作、沉重的生活压力时感到困扰，渴望找到一种方式来提升效率，释放压力？你是否曾经在自我创业的道路上，苦于找不到有效的市场营销方式，寻求突破&#xff1f…...

编程日记 2024/1/6 7:27:04

【Spring实战】22 Spring Actuator 入门

文章目录 1. 定义2. 功能3. 依赖4. 配置5. 常用的应用场景1）环境监控2）运维管理3）性能优化 结论 Spring Actuator 是 Spring 框架的一个模块，为开发人员提供了一套强大的监控和管理功能。本文将深入探讨 Spring Actuator 的定义、…...

编程日记 2024/1/6 7:26:03

JSON安全性

确保JSON处理的安全性是现代Web开发中重要的一环。以下是一些关键的安全实践，用于防止JSON注入攻击以及确保数据在传输过程中的安全性： 1. **验证和清洗输入：** - 在将任何数据写入数据库之前，请确保验证用户输入。对于期望的JSON…...

编程日记 2024/1/6 7:25:02

spring-boot-maven插件repackage（goal）的那些事

前言&#xff1a;在打包Springboot项目成jar包时需要在pom.xml使用spring-boot-maven-plugin来增加Maven功能&#xff0c;在我的上一篇博客<<Maven生命周期和插件的那些事&#xff08;2021版&#xff09;>>中已经介绍过Maven和插件的关系&#xff0c;在此不再赘述&…...

编程日记 2024/1/6 7:21:59

ubuntu的boot分区被删除恢复

在鼓捣黑苹果的时候&#xff0c;误删了ubuntu的boot分区&#xff0c;进系统的时候出现emergency mode&#xff0c;那么现在来讲讲怎么恢复 首先做一个ubuntu的启动盘&#xff0c;然后进入启动盘的系统选择试用 呼出命令行&#xff0c;然后添加一个源 sudo add-apt-repository…...

编程日记 2024/1/6 7:20:58

【userfaultfd 条件竞争】starCTF2019 - hackme

前言 呜呜呜&#xff0c;这题不难&#xff0c;但是差不多一个多月没碰我的女朋友 kernel pwn 了&#xff0c;对我的 root 宝宝也是非常想念&#xff0c;可惜这题没有找到我的 root 宝宝&#xff0c;就偷了她的 flag。 哎有点生疏了&#xff0c;这题没看出来堆溢出&#xff0c…...

编程日记 2024/1/6 7:18:56

深度学习中的自动化标签转换：对数据集所有标签做映射转换

在机器学习中&#xff0c;特别是在涉及图像识别或分类的项目中&#xff0c;标签数据的组织和准确性至关重要。本文探讨了一个旨在高效转换标签数据的 Python 脚本。该脚本在需要更新或更改类标签的场景中特别有用&#xff0c;这是正在进行的机器学习项目中的常见任务。我们将逐…...

编程日记 2024/1/6 7:17:55

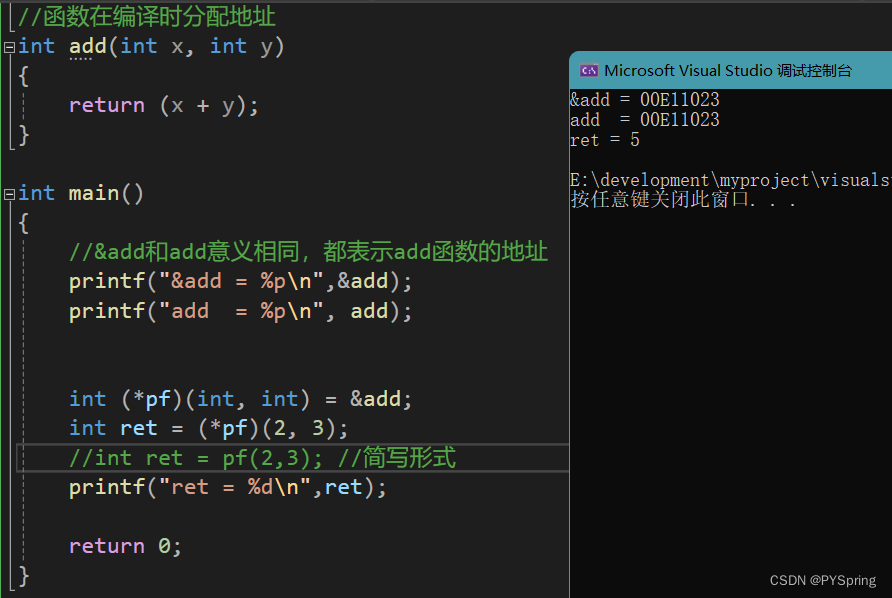
c语言-函数指针

目录 前言一、函数指针1.1 函数指针定义1.2 函数指针调用函数1.3 函数指针代码分析 总结 前言 本篇文章介绍c语言中的函数指针以及函数指针的应用。 一、函数指针 函数指针&#xff1a;指向函数的指针。 函数在编译时分配地址。 &函数名 和 函数名代表的意义相同&#xf…...

编程日记 2024/1/6 7:16:54

conda

一、安装 推荐清华源 https://mirrors.tuna.tsinghua.edu.cn/anaconda/miniconda/?CN&OD选择版本 Miniconda3-py39_4.12.0-MacOSX-arm64.pkg测试命令 conda help二、更换仓库 配置加速 https://mirrors.tuna.tsinghua.edu.cn/help/anaconda/没有 .condarc 文件则执行…...

编程日记 2024/1/6 7:15:53

【Vue】灵魂拷问

1、说说Vue的优缺点 优点&#xff1a;渐进式&#xff0c;组件化&#xff0c;轻量级&#xff0c;虚拟dom&#xff0c;响应式&#xff0c;单页面路由&#xff0c;数据与视图分开缺点&#xff1a;单页面不利于seo&#xff0c;不支持IE8以下&#xff0c;首屏加载时间长 2、为什么…...

编程日记 2024/1/6 7:14:53

Scrapy 1.3.0 使用简介

scrapy 1.3.0 python 2.7 创建一个项目&#xff1a; Before you startscraping, you will have to set up a new Scrapy project. Enter a directory whereyou’d like to store your code and run: scrapy startproject tutorial 然后就会得到一系列文件&#xff1a; 第一个爬…...

编程日记 2024/1/6 7:10:49

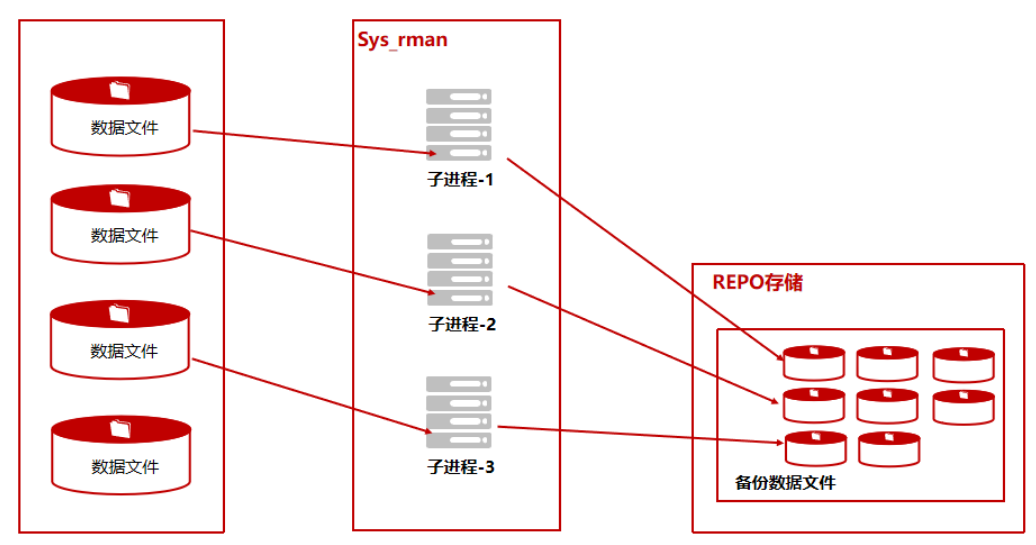
单机+内部备份_全备案例

此场景为单机数据库节点内部备份&#xff0c;方便部署和操作&#xff0c;但备份REPO与数据库实例处于同一个物理主机&#xff0c;冗余度较低。 前期准备 配置ksql免密登录(必须) 在Kingbase数据库运行维护中&#xff0c;经常用到ksql工具登录数据库&#xff0c;本地免密登录…...

编程日记 2024/1/6 7:08:47

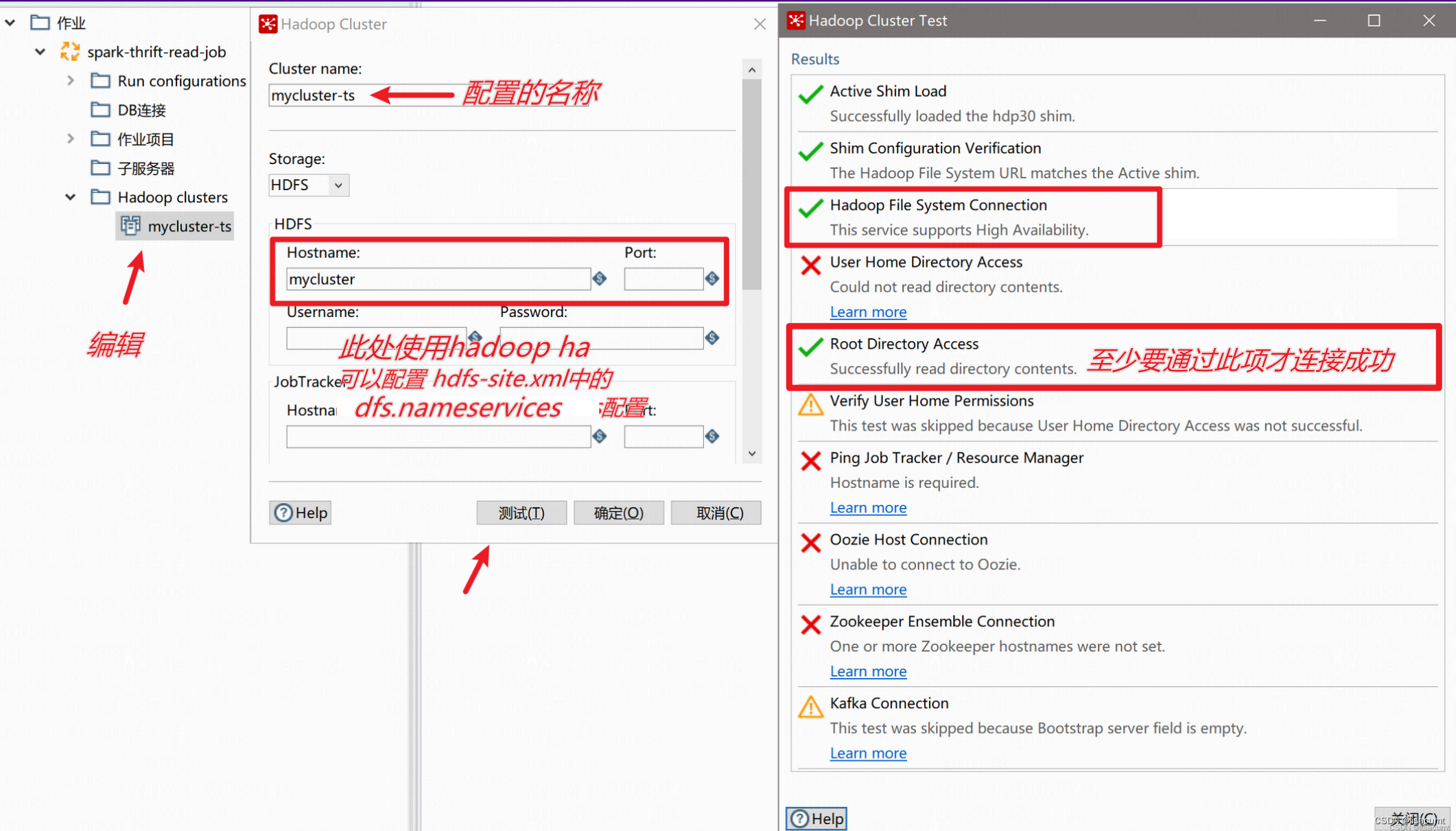
【kettle】pdi/data-integration 打开ktr文件报错“Unable to load step info from XML“

一、报错内容&#xff1a; Unable to load step info from XML step nodeorg.pentaho.di.core.exception.KettleXMLException: Unable to load step info from XMLat org.pentaho.commons.launcher.Launcher.main (Launcher.java:92)at java.lang.reflect.Method.invoke (Met…...

编程日记 2024/1/6 7:05:44

cocos creator人开发小游戏免费素材资源

1、首先熟悉官方的手册和api文档&#xff0c;文档还是比较详细&#xff0c;游戏的方方面面都涉及到了 官方手册&#xff1a; http://docs.cocos.com/creator/manual/zh/官方api文档&#xff1a; http://docs.cocos.com/creator/api/zh/官方论坛&#xff1a; https://forum.coco…...

编程日记 2024/1/6 7:04:43

除了sd webui，compfy还有一个sd UI

GitHub - VoltaML/voltaML-fast-stable-diffusion: Beautiful and Easy to use Stable Diffusion WebUI...

编程日记 2024/1/6 7:03:41

c++属于同一个类的不同对象之间可相互访问private和protected成员

先看一个代码例子&#xff1a; #include <stdio.h>class A { private:char* name;void printA_Name() const {printf(name);} public:A(char* name) {this->name name;}void printA_Name(const A& a) {printf(a.name);}void printA_Name2(const A& a) {a.pr…...

编程日记 2024/1/6 7:01:39

Docker 离线安装指南

参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性&#xff0c;不同版本的Docker对内核版本有不同要求。例如&#xff0c;Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本&#xff0c;Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

编程新知 2026/1/11 12:19:01

Admin.Net中的消息通信SignalR解释

定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

编程新知 2025/9/10 5:36:56

srs linux

下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935&#xff0c;SRS管理页面端口是8080&#xff0c;可…...

编程新知 2026/1/1 7:15:20

React19源码系列之 事件插件系统

事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

编程新知 2026/1/6 2:54:13

第一篇：Agent2Agent (A2A) 协议——协作式人工智能的黎明

AI 领域的快速发展正在催生一个新时代&#xff0c;智能代理&#xff08;agents&#xff09;不再是孤立的个体&#xff0c;而是能够像一个数字团队一样协作。然而&#xff0c;当前 AI 生态系统的碎片化阻碍了这一愿景的实现&#xff0c;导致了“AI 巴别塔问题”——不同代理之间…...

编程新知 2025/12/30 22:13:49

GitHub 趋势日报 (2025年06月08日)

&#x1f4ca; 由 TrendForge 系统生成 | &#x1f310; https://trendforge.devlive.org/ &#x1f310; 本日报中的项目描述已自动翻译为中文 &#x1f4c8; 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

编程新知 2025/12/13 1:32:15

自然语言处理——Transformer

自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效&#xff0c;它能挖掘数据中的时序信息以及语义信息&#xff0c;但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN&#xff0c;但是…...

编程新知 2026/1/3 0:10:19

Reasoning over Uncertain Text by Generative Large Language Models

https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达，从日常对话到特定领域的文档（例如医学文档）（Heritage 2013；Landmark、Gulbrandsen 和 Svenevei…...

编程新知 2026/1/10 1:38:15

使用LangGraph和LangSmith构建多智能体人工智能系统

现在&#xff0c;通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战&#xff0c;比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

编程新知 2025/12/30 22:02:21

解读《网络安全法》最新修订，把握网络安全新趋势

《网络安全法》自2017年施行以来&#xff0c;在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂&#xff0c;网络攻击、数据泄露等事件频发&#xff0c;现行法律已难以完全适应新的风险挑战。 2025年3月28日&#xff0c;国家网信办会同相关部门起草了《网络安全…...

编程新知 2026/1/2 19:20:41