【已解决】js定义对象属性是.如何访问
当变量没有length属性的时候,可能是个对象变量,当有键值对的时候就可能是个对象,读者都知道的是,用typeof(变量)可以查看属性,今天本文解决的问题是如果js定义对象中属性是"点"如何访问
问题再现
var a = {"a.b":[1,2,3]};
如何访问到[1,2,3],一般我会想到用a.a.b来访问,但结果不尽人意
问题解决方案

a["a.b"]
Array(3) [ 1, 2, 3 ]
总结
当定义对象有.属性的时候,犹如文中,就不能用.属性名来访问,只需要用中括号来访问,博文从表及理去演示了如何解决js定义对象属性是.如何访问的问题,堪称值得收藏的好文章,感谢读者阅读到这里,谢谢!
相关文章:

【已解决】js定义对象属性是.如何访问
当变量没有length属性的时候,可能是个对象变量,当有键值对的时候就可能是个对象,读者都知道的是,用typeof(变量)可以查看属性,今天本文解决的问题是如果js定义对象中属性是"点"如何访问 问题再现 var a {…...
Linux入门攻坚——11、Linux网络属性配置相关知识1
网络基础知识: 局域网:以太网,令牌环网, Ethernet:CSMA/CD 冲突域 广播域 MAC:Media Access Control,共48bit,前24bit需要机构分配,后24bit自己…...
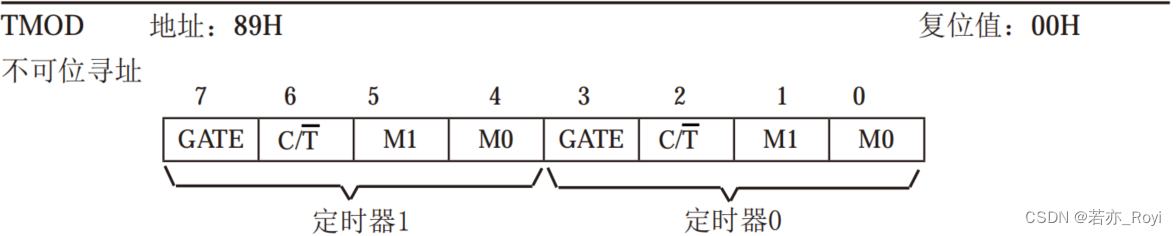
51单片机定时/计数器相关知识点
51单片机定时/计数器相关知识点 结构组成 51单片机的定时/计数器中有两个寄存器: T0:低位:TL0(字节地址8AH)高位:TH0(字节地址8CH)T1:低位:TL1(…...

机器视觉兄弟们,没有项目订单,机器视觉项目行业难题来了
产品没一个正形,光源像是打了几十年的光棍一样,偏偏配不上,n次“相亲”之后图像硬是“阴晴圆缺”,老板阴阳怪气你这打不出来,给客户看之后说,这都打不出来,你们不行啊。 我听了后真想ÿ…...

机器人开发--动力系统
机器人开发--动力系统 1 介绍概述BMS电池管理芯片系电源管理细分赛道,主要产品形态包括电池计量(电量计)、电池安全、充电管理等三大类芯片BMS 产业链动力电源、消费电子细分领域 BMS 芯片种类、技术及下游销量概览 电池电池包典型产品及参数…...
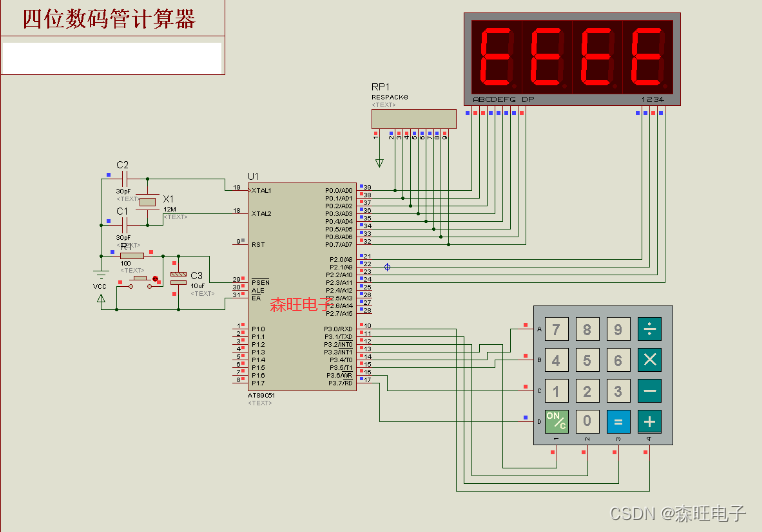
51单片机四位数码管计算器 Proteus仿真程序
目录 概要 仿真图 部分代码 资料下载地址:51单片机四位数码管计算器 Proteus仿真程序 概要 1.系统通过4x4的矩阵键盘输入数字及运算符。 2.可以进行4位十进制数以内的加法运算,如果计算结果超过4位十进制数,则屏幕显示E 3.可以进行加法以外…...

问题 B: 分牌
题目描述 有 N 堆纸牌,编号分别为 1,2,…, N。每堆上有若干张,但纸牌总数必为 N 的倍数。可以在任一堆上取若干张纸牌,然后移动。 移牌规则为:在编号为 1 堆上取的纸牌,只能移到编号为 2 的堆上…...
3元一平方公里的在线卫星影像
我们为大家分享了免费下载卫星影像的方法。 但让人遗憾的是,该影像的最高分辨率只有10米,需要更高清且比较新的卫星影像,看来还是得付费购买才比较靠谱。 自助选择区县范围 商业卫星影像主要面向企事业单位,一般来讲都比较贵&a…...
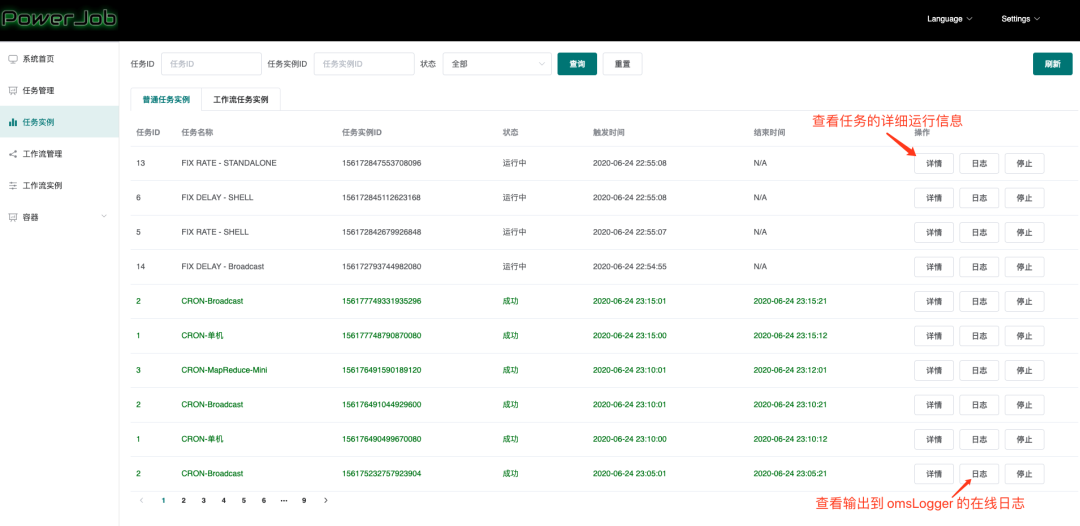
只会用 xxl-job?更强大的新一代分布式任务调度框架来了!
前言 PowerJob是新一代分布式任务调度与计算框架,支持CRON、API、固定频率、固定延迟等调度策略,提供工作流来编排任务解决依赖关系,能让您轻松完成作业的调度与繁杂任务的分布式计算。 文章来源:https://blog.csdn.net/LY_624/…...

LeetCode-无重复字符的最长子串(3)
题目描述: 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 代码: class Solution {public int lengthOfLongestSubstring(String s) {Set<Character> occnew HashSet<Character>();int lens.length();int…...
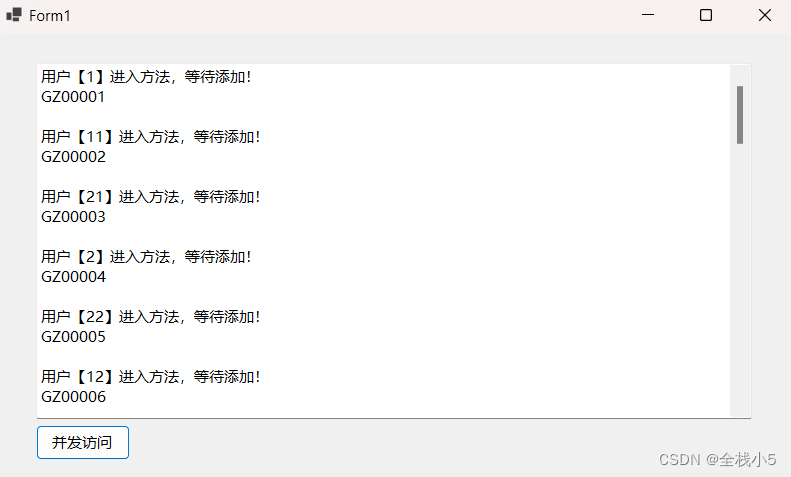
【C#】知识点实践序列之Lock简单解决并发引起数据重复问题
欢迎来到《小5讲堂之知识点实践序列》文章,大家好,我是全栈小5。 这是2024年第3篇文章,此篇文章是C#知识点实践序列文章,博主能力有限,理解水平有限,若有不对之处望指正! 本篇在Lock锁定代码块基…...

NLP基础——TF-IDF
TF-IDF TF-IDF全称为“Term Frequency-Inverse Document Frequency”,是一种用于信息检索与文本挖掘的常用加权技术。该方法用于评估一个词语(word)对于一个文件集(document)或一个语料库中的其中一份文件的重要程度。…...
)
kubernetes(四)
文章目录 1. 持久化存储1.1 HostPath1.2 NFS1.3 PV和PVC 1. 持久化存储 1.1 HostPath hostpath:多个容器共享数据,不能跨宿主机,如果宿主机挂了,在其他宿主机上起pod,那么之前的数据就没有了 spec:nodeName: 10.0.0…...
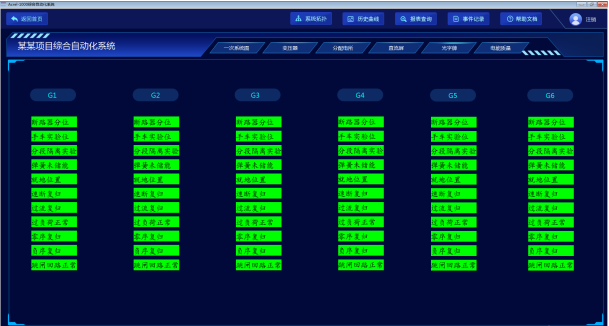
安科瑞变电站综合自动化系统在青岛海洋科技园应用——安科瑞 顾烊宇
摘 要:变电站综合自动化系统是将变电站内的二次设备经过功能的组合和优化设计,利用先进的计算机技术、通信技术、信号处理技术,实现对全变电站的主要设备和输、配电线路的自动监视、测量、控制、保护、并与上级调度通信的综合性自动化功能。 …...

紫光展锐5G扬帆出海 | 欧洲积极拥抱更多5G选择
和我国一样,欧洲不少国家也在2019年进入5G商用元年:英国在2019年5月推出了5G商用服务,该国最大的移动运营商EE(Everything Everywhere)最先商用5G;德国在2019年年中推出5G商用服务,德国电信、沃达丰和 Telefonica是首批…...

Open3D聚类算法
按照官网的例子使用聚类,发现结果是全黑的。 经过多次测试发现 eps3.3, min_points1这里是关键 min_points必须等于1否则无效果 import time import open3d as o3d; import numpy as np; import matplotlib.pyplot as plt#坐标 mesh_coord_frame o3d.geometry.Tria…...
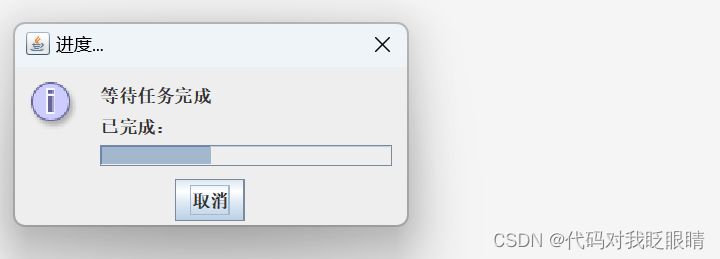
swing快速入门(三十九)进度对话框
🎁注释很详细,直接上代码 🧧新增内容 🧨1.模拟耗时操作 🧨2.使用计时器更新进度对话框 🎀源码: package swing31_40;import javax.swing.*; import java.awt.event.ActionEvent; import java.aw…...

Oracle-存储过程
简介 存储过程(Stored Procedure)是一组为了完成特定功能的SQL语句集,它大大提高了SQL语句的功能和灵活性。存储过程编译后存储在数据库中,所以执行存储过程比执行存储过程中封装的SQL语句更有效率。 语法 存储过程: 一组为了完成某种特定功能的sql语句…...
L1-085:试试手气
我们知道一个骰子有 6 个面,分别刻了 1 到 6 个点。下面给你 6 个骰子的初始状态,即它们朝上一面的点数,让你一把抓起摇出另一套结果。假设你摇骰子的手段特别精妙,每次摇出的结果都满足以下两个条件: 1、每个骰子摇出…...
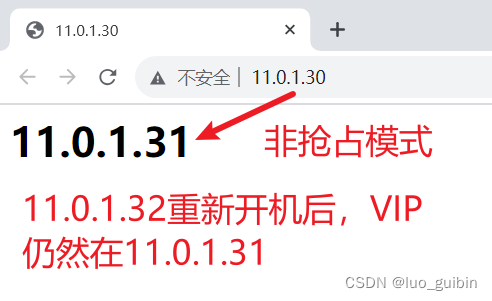
nginx+keepalived实现七层负载
目录 一、部署nginx01、nginx02 二、keepalived配置(抢占模式、master- backup模式) 三、测试 四、非抢占模式(backup-backup模式) nginx01 11.0.1.31nginx0211.0.1.32虚拟IP(VIP)11.0.1.30 一、部署ngin…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
