[蓝桥杯] 数学与简单DP问题

文章目录
一、简单数学问题习题练习
1、1 买不到的数目
1、1、1 题目描述
1、1、2 题解关键思路与解答
1、2 饮料换购
1、2、1 题目描述
1、2、2 题解关键思路与解答
二、DP问题习题练习
2、1 背包问题
2、1、1 题目描述
2、1、2 题解关键思路与解答
2、2 摘花生
2、2、1 题目描述
2、2、2 题解关键思路与解答
2、3 最长上升子序列
2、3、1 题目描述
2、3、2 题解关键思路和解答
三、总结
标题:蓝桥杯——数学与简单DP问题习题练习
作者:@Ggggggtm
寄语:与其忙着诉苦,不如低头赶路,奋路前行,终将遇到一番好风景

一、简单数学问题习题练习
蓝桥杯比赛中常见的还有一类数学问题,这些数学问题有的是有公式计算,有的是考察的思维逻辑。我们具体来看例题。
1、1 买不到的数目
1、1、1 题目描述
题目来源:第四届蓝桥杯省赛C++A组,第四届蓝桥杯省赛JAVAC组
题目难度:简单
题目描述:小明开了一家糖果店。他别出心裁:把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。小朋友来买糖的时候,他就用这两种包装来组合。当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
输入格式:
两个正整数 n,m,表示每种包装中糖的颗数。
输出格式:
一个正整数,表示最大不能买到的糖数。
数据范围:
2≤n,m≤1000,
保证数据一定有解。输入样例:
4 7输出样例:
17
1、1、2 题解关键思路与解答
我们先关插题目,是两个数找到这两个数最大凑不出来的数。当两个数是由除1外还有其他的公约数时,我们发现并不能找到这两个数最大凑不出来的数。也就是当两个数互质时,才能够找出这两个数最大凑不出来的数。这里是有一个公式的,我们假设这两个数分别是p、q,两个数互质,那么求这两个数最大凑不出来的数的公式为:(p-1)*(q-1)-1。我们看一下本题的代码。
#include<iostream>using namespace std;int p,q;int main()
{cin>>p>>q;cout<<(p-1)*(q-1)-1;return 0;
}1、2 饮料换购
1、2、1 题目描述
题目来源:第六届蓝桥杯省赛C++A/C组,第六届蓝桥杯省赛JAVAB组
题目难度:简单
题目描述:乐羊羊饮料厂正在举办一次促销优惠活动。乐羊羊C型饮料,凭3个瓶盖可以再换一瓶C型饮料,并且可以一直循环下去(但不允许暂借或赊账)。请你计算一下,如果小明不浪费瓶盖,尽量地参加活动,那么,对于他初始买入的 n 瓶饮料,最后他一共能喝到多少瓶饮料。
输入格式:
输入一个整数 n,表示初始买入的饮料数量。
输出格式:
输出一个整数,表示一共能够喝到的饮料数量。
数据范围:
0<n<10000。
输入样例:
100输出样例:
149
1、2、2 题解关键思路与解答
本题目主要考察的是思维逻辑能力。我们要注意的是本题有一个陷阱,就是我们需要注意用瓶盖换瓶子的时候可能会有剩余,下次再换的时候我们的瓶盖数量就是已经换购的饮料数量加喝完上上次剩下的瓶盖数量。我们直接看代码。
#include<iostream>using namespace std;int n;int main()
{cin>>n;int sum=n;int ret=n;while(ret >= 3){sum+=ret/3;ret=ret/3+ret%3;}cout<< sum;return 0;
}二、DP问题习题练习
2、1 背包问题
2、1、1 题目描述
题目来源:AcWing
题目难度:简单
题目描述:有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式:
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式:
输出一个整数,表示最大价值。
数据范围:
0<N,V≤1000,
0<vi,wi≤1000。输入样例:
4 5 1 2 2 4 3 4 4 5输出样例:
8
2、1、2 题解关键思路与解答
这里我们用闫氏DP分析法进行分析:
上述思想的关键就是状态计算。我们不选第 i 个物品时,其前 i-1个物品的总价值和为 f[i-1][j],那么第 i 个物品的价值也为 f[i-1][j]。如我们选上第 i 个物品时,计算其价值为前 i-1 个物品的价值表示为 f[i-1][j-v[i]],那么选上第i个物品的价值为 f[i-1][j-v[i]] + w[i]。在两者值减去一个较大的就行。我们看代码的实现。
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N =1010;int f[N][N];int n,m;int v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);}}cout<<f[n][m]<<endl;return 0;
}2、2 摘花生
2、2、1 题目描述
题目来源:《信息学奥赛一本通》
题目难度:简单
题目描述:Hello Kitty想摘点花生送给她喜欢的米老鼠。她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。Hello Kitty只能向东或向南走,不能向西或向北走。问Hello Kitty最多能够摘到多少颗花生。
输入格式:
第一行是一个整数T,代表一共有多少组数据。
接下来是T组数据。
每组数据的第一行是两个整数,分别代表花生苗的行数R和列数 C。
每组数据的接下来R行数据,从北向南依次描述每行花生苗的情况。每行数据有C个整数,按从西向东的顺序描述了该行每株花生苗上的花生数目M。
输出格式:
对每组输入数据,输出一行,内容为Hello Kitty能摘到得最多的花生颗数。
数据范围:
1≤T≤100,
1≤R,C≤100,
0≤M≤1000。输入样例:
2 2 2 1 1 3 4 2 3 2 3 4 1 6 5输出样例:
8 16
2、2、2 题解关键思路与解答
该题我们同样用闫氏DP分析法:
状态计算中的集合划分大部分情况下的依据是最后不相同的一步。这道题就是走到右下角只能是从正上走过来,或者正左走过来。我们只需要选出这两者的较大的一个,再加上右下角的花生数量即可。我们结合着代码一起理解一下。
#include<iostream>using namespace std;const int N=110;int f[N][N],w[N][N];int n,m;int main()
{int T=0;cin>>T;while(T--){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&w[i][j]);}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){f[i][j]=max(f[i-1][j],f[i][j-1])+w[i][j];}}cout<<f[n][m]<<endl;}return 0;
}
2、3 最长上升子序列
2、3、1 题目描述
题目来源:AcWing
题目难度:简单
题目描述:给定一个长度为 N 的数列,求数值严格单调递增的子序列的长度最长是多少。
输入格式:
第一行包含整数 N。
第二行包含 N 个整数,表示完整序列。
输出格式:
输出一个整数,表示最大长度。
数据范围:
1≤N≤1000,
−1e9≤数列中的数≤1e9。输入样例:
7 3 1 2 1 8 5 6输出样例:
4
2、3、2 题解关键思路和解答
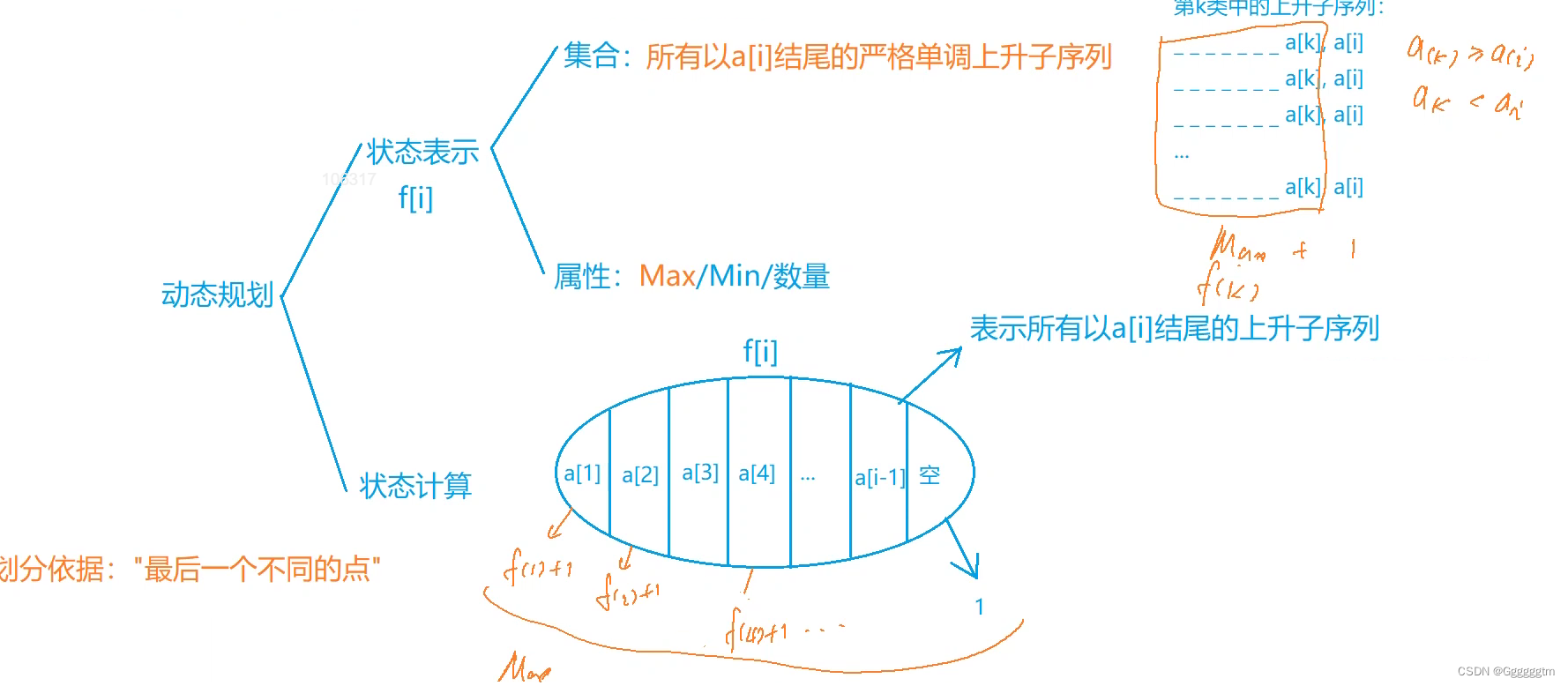
该题目可能会给很多同学造成一个错误的理解。题目中的要求是求数值严格单调递增的子序列的长度最长是多少,指的是不是连续的也行。如上述案例,最大上升子序列为:1,2,5,6。那该怎么求呢?我们用闫氏DP法进行分析:
这里关键的就是我们枚举出以i结尾的最大的长度即可。最后在从不同结尾当中找出最大值。那我们怎么计算出以i结尾的最大长度呢?我们只需要在i之前,且比 a[i] 的就行,更新 f[i] 的值即可。我们结合着代码一起理解一下:
#include<iostream>using namespace std;const int N=1010;int a[N],f[N];int main()
{int n;cin>>n;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++){f[i]=1;for(int j=1;j<i;j++){if(a[j]<a[i])f[i]=max(f[i],f[j]+1);}}int res=0;for(int i=1;i<=n;i++)res=max(res,f[i]);cout<<res;return 0;
}三、总结
关于数学的问题,我们主要是对刷题进行练习巩固。DP动态规划的问题大多数情况是有固定的分析路线,也是需要多加做题练习。
今天的练习就到这里,希望以上内容对你有所帮助,感谢观看。
相关文章:
[蓝桥杯] 数学与简单DP问题
文章目录 一、简单数学问题习题练习 1、1 买不到的数目 1、1、1 题目描述 1、1、2 题解关键思路与解答 1、2 饮料换购 1、2、1 题目描述 1、2、2 题解关键思路与解答 二、DP问题习题练习 2、1 背包问题 2、1、1 题目描述 2、1、2 题解关键思路与解答 2、2 摘花生 2、2、1 题目…...
浏览器的渲染过程解析
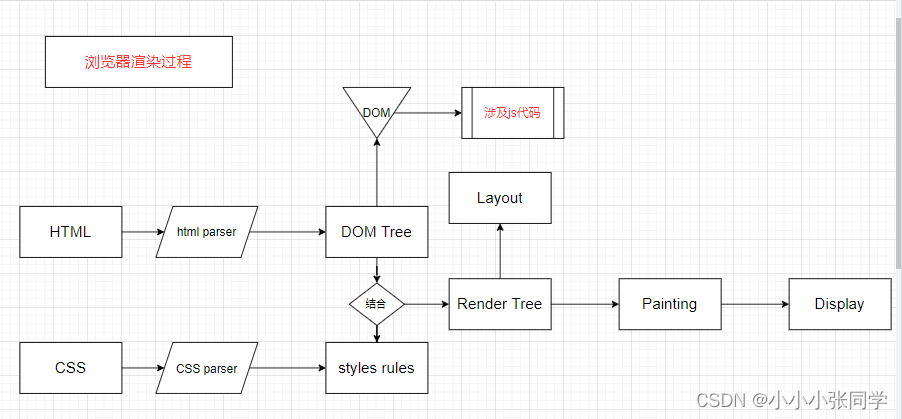
文章目录浏览器渲染进程有哪些?浏览器的渲染过程浏览器渲染进程有哪些? GUI线程:负责渲染浏览器页面,解析html,css,构建DOM树,CSS规则树,渲染树和绘制页面,当界面需要重…...

【C++容器】std::fstream读写文件错误【2023.03.03】
std::fstream使用细节 1.文件不存不支持时打开文件模式不得有ios::in • 如果文件不存在且打开时包括了ios::in模式则打开文件会失败。 fstream m_f;m_f.open("d://123.csv", ios::in | ios::out | ios::binary);//文件不存在则会打开失败• 我这边尝试行得通的做…...
UVM实战--带有寄存器的加法器
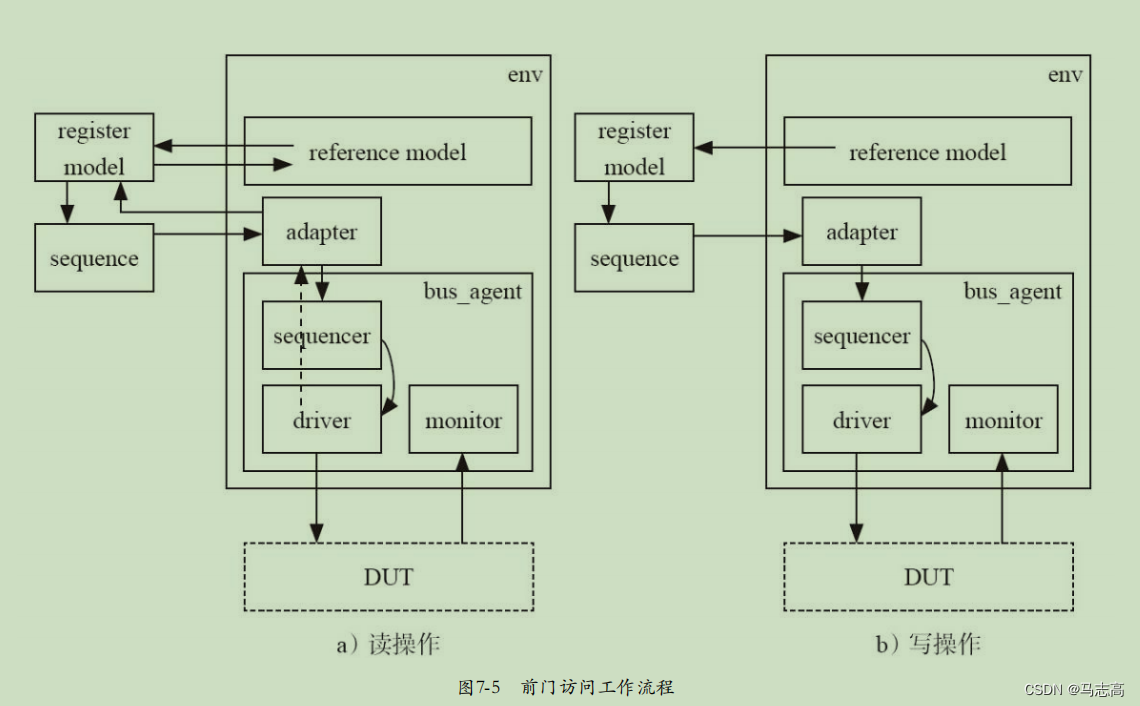
一.整体的设计结构图 这里将DUT换成加法器,可以理解为之前UVM加法器加上寄存器,这里总线的功能不做修改,目的看代码的移植那些部分需要修改。 二.各个组件代码详解 2.1 DUT module dut( input clk, input rst_n, input…...
笔记--学习mini3d代码
主要是记录学习mini3d代码时,查的资料; 从github下载的代码: GitHub - skywind3000/mini3d: 3D Software Renderer in 700 Lines !!3D Software Renderer in 700 Lines !! Contribute to skywind3000/mini3d development by creating an a…...
图片服务器
文章目录一、项目简介二、功能及场景三、业务设计四、数据库设计准备图片表准备实体类五、API设计常用功能封装文件上传文件上传获取图片列表接口获取图片内容删除图片接口六、项目优化七、测试自动化测试测试用例一、项目简介 图片服务器:解决项目中插入图片的问题…...
【JAVA程序设计】【C00110】基于SSM(非maven)的车辆维修管理系统
基于SSM(非maven)的车辆维修管理系统项目简介项目获取开发环境项目技术运行截图项目简介 基于ssm框架非maven开发的车辆维修管理系统共分为三个角色:管理员、用户 管理员角色包含以下功能: 查看用户、添加用户、查看车辆信息、故…...
【中学里的解题技巧】)
微积分小课堂:用动态的眼光去找问题的最优解(最大值/最小值)【中学里的解题技巧】
文章目录 引言I 最优化问题1.1 不同形式的最优化1.2 用动态的眼光去找问题的最优解引言 把比较数大小的问题,变成了寻找函数变化拐点的问题,将这两个问题等同起来,需要发明一种工具,叫做导数。有了导数这个工具,求最大值问题就变成了解方程的问题。 用变化的眼光找到最优…...

网络爬虫和相关工具
在理想的状态下,所有ICP(Internet Content Provider)都应该为自己的网站提供API接口来共享它们允许其他程序获取的数据,在这种情况下爬虫就不是必需品,国内比较有名的电商平台(如淘宝、京东等)、…...
OSSFs挂载工具简介
OSSFs挂载工具 OSSFs挂载工具简介 ossfs允许您在Linux系统中将对象存储OSS的存储空间(Bucket)挂载到本地文件系统。挂载完成后,您能够像操作本地文件一样操作OSS的对象(Object),从而实现数据共享。 …...

Spring 容器创建初始化,获取bean流程分析
Spring 容器创建初始化,获取bean流程分析 Spring 容器创建初始化 流程分析 1、首先读取bean.xml 文件 2、扫描指定的包 com.hspedu.spring.component 2.1、扫描包,得到bean的class对象,排除包下不是bean的 2.2、扫描将bean信息封装BeanDef…...
无聊小知识.03 Springboot starter配置自动提示
1、前言Springboot项目配置properties或yaml文件时候,会有很多spring相关的配置提示。这个是如何实现的?如果我们自己的配置属性,能否也自动提示?2、Springboot配置自动提示其实IDE是通过读取配置信息的元数据而实现自动提示的。S…...

2023-03-03 mysql-join类别-分析
目录 摘要: mysql版本: DDL: 表结构: 插入数据: JOIN: 一. SELECT 二. INNER JOIN...

Saleen 系列来袭!
由 Ghostopunch 创作👻🥊 Ghostpunch 将 Saleen Automotive 带入 The Sandbox 元宇宙! 是 Saleen Automotive 于 1984 年由汽车界的梦想家 Steve Saleen 创立,目标是将经过比赛验证的性能带入大街小巷和元宇宙……😉 5…...

如何优雅地处理Java中的null值?使用Optional类来实现!
当我们在Java编程时,经常会遇到处理null值的问题。在Java 8中,引入了一个Optional类来解决这个问题。Optional类可以看作是一个容器,用于包装一个可能为null的值。它提供了一些方便的方法,以优雅地处理null值的情况。 下面我将详…...

巾帼绽芬芳 一起向未来(中篇)
编者按:为了隆重纪念纪念“三八”国际妇女节113周年,快来与你全方位、多层次分享交流“三八”国际妇女节的前世今生。分上篇(节日简介、节日发展和节日意义)、中篇(节日活动宗旨和世界各国庆祝方式)和下篇&…...

espnet training
from:ESPnet2 — ESPnet 202301 documentation from :Change the configuration for training — ESPnet 202301 documentation 训练完之后微调的命令: ./run.sh --stage 11 --ngpu 1 --asr_args "--max_epoch 205 --optim_conf lr=0.1 --resume true" --asr_exp…...

qsort函数的应用以及模拟实现
前言 🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨ 🐻推荐专栏: 🍔🍟🌯 c语言进阶 🔑个人信条: 🌵知行合一 🍉本篇简介:>:介绍库函数qsort函数的模拟实现和应用 金句分享: ✨追…...
【iobit 软件】家族系列 - 正版激活码
装机必备iobit系列软件 - 激活码获取看最后 第一款、Advanced SystemCare 16 您需要的人工智能驱动的PC优化器,以释放磁盘空间,加速PC并保护在线隐私。 功能特点: 1. 系统清理与优化:通过清除系统垃圾文件、注册表信息、无用文…...
ACM-大一训练第三周(Floyd算法+并查集算法专题训练)
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石.CSDN 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:ACM周训练题目合集.CSDN 💬总结:…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...

Linux入门(十五)安装java安装tomcat安装dotnet安装mysql
安装java yum install java-17-openjdk-devel查找安装地址 update-alternatives --config java设置环境变量 vi /etc/profile #在文档后面追加 JAVA_HOME"通过查找安装地址命令显示的路径" #注意一定要加$PATH不然路径就只剩下新加的路径了,系统很多命…...

Redis——Cluster配置
目录 分片 一、分片的本质与核心价值 二、分片实现方案对比 三、分片算法详解 1. 范围分片(顺序分片) 2. 哈希分片 3. 虚拟槽分片(Redis Cluster 方案) 四、Redis Cluster 分片实践要点 五、经典问题解析 C…...