差分约束算法
差分约束
差分约束系统包含 m m m个涉及 n n n个变量的差额限制条件,这些差额限制条件每个都是形式为 x i − x j ≤ b ∈ [ 1 , m ] x_i-x_j\leq b_{\in[1,m]} xi−xj≤b∈[1,m]的简单线性不等式。
通常我们要求解出一组可行解。
最短路差分约束
如果我们把变量看做节点,如果这里用 d u d_u du表示 d i s S , u dis_{S,u} disS,u,那么从 u u u到 v v v的一条有向边必然满足 d u + w ≥ d v d_u+w\geq d_v du+w≥dv,即:
d v − d u ≤ w d_v-d_u\leq w dv−du≤w
对比:
x v − x u ≤ b i x_v-x_u\leq b_i xv−xu≤bi
因此对于每个限制条件 x v − x u ≤ b i x_v-x_u\leq b_i xv−xu≤bi,我们可以在图上给 u u u到 v v v连接一条边权为 b i b_i bi的有向边。
同时建立一个虚拟源点 S S S,向着每个点连接一个长度为 0 0 0的边。
如果图中不存在负环,那么可以使用单源最短路径算法求出所有的 d u d_u du,则 x i = d i x_i=d_i xi=di就是原问题的一组可行解。如果有负环说明无解。
定理:图中没有负环是差分约束系统有解的充要条件。
充分性显然,因为我们可以构造出一组解。
必要性:
如果图中存在负环,那么说明此差分约束系统无解:
设图中有一个负环, w 1 + w 2 + w 3 < 0 w_1+w_2+w_3<0 w1+w2+w3<0
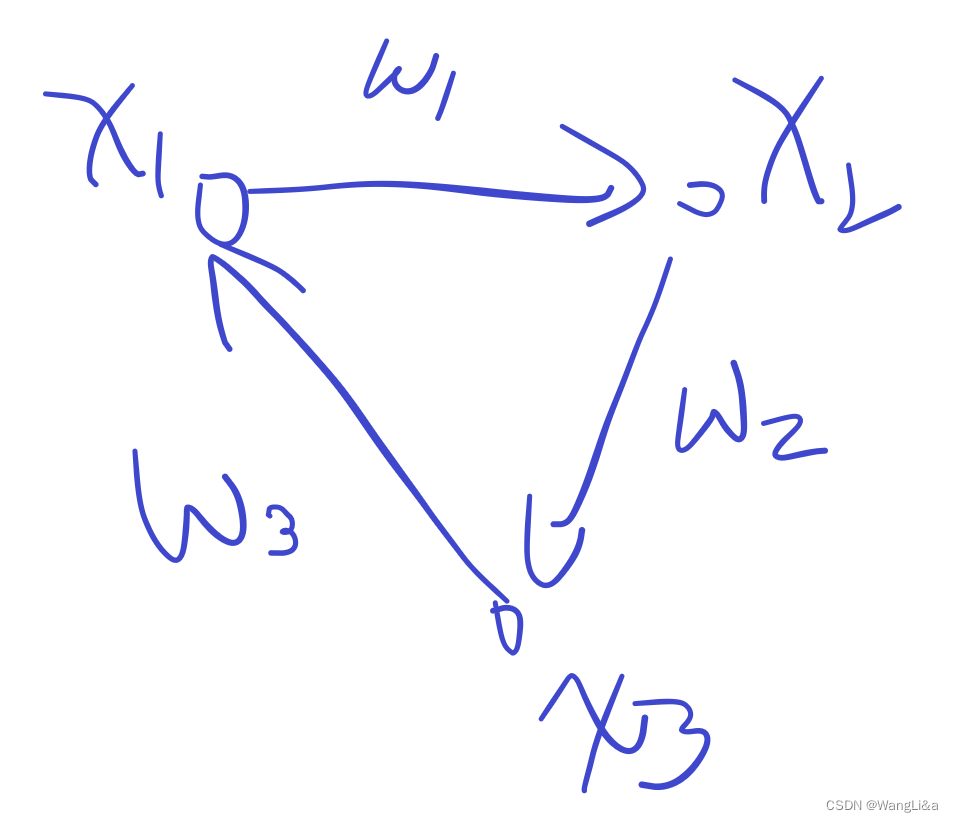
x 1 + w 1 ≥ x 2 x_1+w_1\geq x_2 x1+w1≥x2
x 1 + w 1 + w 2 ≥ x 2 + w 2 ≥ x 3 x_1+w_1+w_2\geq x_2+w_2\geq x_3 x1+w1+w2≥x2+w2≥x3
x 1 + w 1 + w 2 + w 3 ≥ x 3 + w 3 ≥ x 1 x_1+w_1+w_2+w_3 \geq x_3+w_3\geq x_1 x1+w1+w2+w3≥x3+w3≥x1
x 1 + w 1 + w 2 + w 3 ≥ x 1 x_1+w_1+w_2+w_3 \geq x_1 x1+w1+w2+w3≥x1
这说明 x 1 + 一个负数 ≥ x 1 x_1+一个负数\geq x_1 x1+一个负数≥x1,这是不可能的,因此这个差分约束系统是矛盾的,无解。
QED.
性质
这样建图跑最短路求出的解是具有一定性质的,具体来说是:
- x i ∈ [ 1 , n ] ≤ 0 x_{i\in[1,n]}\leq 0 xi∈[1,n]≤0
- 对于任意差分约束系统的一组解 { x n ′ } \left\{x'_{n}\right\} {xn′}满足 x i ∈ [ 1 , n ] ′ ≤ 0 x'_{i\in[1,n]}\leq 0 xi∈[1,n]′≤0,都有 x i ≥ x i ′ ( i ∈ [ 1 , n ] ) x_i\geq x'_i(i\in[1,n]) xi≥xi′(i∈[1,n]),也就称为最大解
- 对于所有解 x i ∈ [ 1 , n ] ′ ≤ 0 x'_{i\in[1,n]}\leq 0 xi∈[1,n]′≤0,都有 ∑ n i = 1 x i ≥ ∑ n i = 1 x i ′ \underset{i=1}{\overset n\sum}x_i\geq\underset{i=1}{\overset n\sum}x'_i i=1∑nxi≥i=1∑nxi′
证明:
只需证明性质2,性质1、3显然:
首先考虑虚拟源点 S S S的意义,即我们令 x S x_S xS表示一个新量,我们连零边表示: x i ∈ [ 1 , n ] − x S ≤ 0 x_{i\in[1,n]}-x_S\leq 0 xi∈[1,n]−xS≤0。
然后我们在跑最短路时强制 x S = d S = 0 x_S=d_S=0 xS=dS=0,因此我们连零边实际上限制了: x i ∈ [ 1 , n ] ≤ 0 x_{i\in[1,n]}\leq 0 xi∈[1,n]≤0
接下来考虑:
对于 x i = d i x_i=d_i xi=di,假设其对应的某条从 S S S到 i i i的最短路径依次经过了点 u 0 = S , u 1 , u 2 , . . . , u k = i u_0=S,u_1,u_2,...,u_k=i u0=S,u1,u2,...,uk=i,则经过的边对应的不等式为:
x u j − x u j − 1 ≤ w j x_{u_j}-x_{u_{j-1}}\leq w_j xuj−xuj−1≤wj
求和得到:
∑ k j = 1 x u j − x u j − 1 ≤ ∑ k j = 1 w j \underset{j=1}{\overset k\sum}x_{u_j}-x_{u_{j-1}}\leq \underset{j=1}{\overset k\sum} w_j j=1∑kxuj−xuj−1≤j=1∑kwj
由于裂项:
x u k − x u 0 ≤ ∑ k j = 1 w j x_{u_k}-x_{u_0}\leq \underset{j=1}{\overset k\sum}w_j xuk−xu0≤j=1∑kwj
由于我们指定了 x S = 0 x_S=0 xS=0,也就是说:
x i ≤ ∑ k j = 1 w j x_i\leq \underset{j=1}{\overset k\sum}w_j xi≤j=1∑kwj
这给出了此差分约束系统中,满足所有变量都 ≤ 0 \leq 0 ≤0的任意一个解中, x i x_i xi的一个上界。
同时我们断言这个上界是可以取到的,并且 x i = d i = ∑ k j = 1 w j x_i=d_{i}=\underset{j=1}{\overset k\sum}w_j xi=di=j=1∑kwj,原因如下,因为刚才经过的边事实上是由 S S S到 i i i的最短路径,根据相关理论,我们有:
d i s S , u j − d i s S , u j − 1 = w j dis_{S,u_j}-dis_{S,u_{j-1}}=w_j disS,uj−disS,uj−1=wj
求和得到:
∑ k j = 1 d i s S , u j − d i s S , u j − 1 = ∑ k j = 1 w j \underset{j=1}{\overset k\sum}dis_{S,u_j}-dis_{S,u_{j-1}}= \underset{j=1}{\overset k\sum} w_j j=1∑kdisS,uj−disS,uj−1=j=1∑kwj
由于裂项:
d i s S , i = ∑ k j = 1 w j dis_{S,i}=\underset{j=1}{\overset k\sum}w_j disS,i=j=1∑kwj
因此我们知道 x i = d i = d i s S , i = ∑ k j = 1 w j x_i=d_i=dis_{S,i}=\underset{j=1}{\overset k\sum}w_j xi=di=disS,i=j=1∑kwj,证明上界可以取到。
QED.
最长路差分约束
如果我们用 d u d_u du表示 S S S到 u u u的最长路,那么对于有向边 ( u , v ) (u,v) (u,v):
d u + w ≤ d v d_u+w\leq d_v du+w≤dv
d u − d v ≤ − w d_u-d_v\leq -w du−dv≤−w
即:
x u − x v ≤ b i x_u-x_v\leq b_i xu−xv≤bi
那么 b i = − w b_i=-w bi=−w,即 w = − b i w=-b_i w=−bi
那么从 u u u向 v v v连接一条长度为 − b i -b_i −bi的有向边。
在从虚拟源点 S S S向着每个点连接一个边权为 0 0 0的有向边。
求出图中的最长路即为差分约束系统的一组解。
同理图中如果存在正环就无解。
性质
这样建图跑最长路求出的解也具有一定性质的,具体来说是:
- x i ∈ [ 1 , n ] ≥ 0 x_{i\in[1,n]}\geq 0 xi∈[1,n]≥0
- 对于任意差分约束系统的一组解 { x n ′ } \left\{x'_{n}\right\} {xn′}满足 x i ∈ [ 1 , n ] ′ ≥ 0 x'_{i\in[1,n]}\geq 0 xi∈[1,n]′≥0,都有 x i ≤ x i ′ ( i ∈ [ 1 , n ] ) x_i\leq x'_i(i\in[1,n]) xi≤xi′(i∈[1,n]),也就称为最小解
- 对于所有解 x i ∈ [ 1 , n ] ′ ≥ 0 x'_{i\in[1,n]}\geq 0 xi∈[1,n]′≥0,都有 ∑ n i = 1 x i ≤ ∑ n i = 1 x i ′ \underset{i=1}{\overset n\sum}x_i\leq\underset{i=1}{\overset n\sum}x'_i i=1∑nxi≤i=1∑nxi′
证明同理。
其他问题
各类限制转化
通常讨论的差分约束问题往往变量为整数,对于一些其他形式的简单线性不等式可以转化为差分约束问题 x − y ≤ b x-y\leq b x−y≤b:
x − y < b ⇒ x − y ≤ b − 1 x-y<b\Rightarrow x-y\leq b-1 x−y<b⇒x−y≤b−1
x − y ≥ b ⇒ y − x ≤ − b x-y\geq b\Rightarrow y-x\leq -b x−y≥b⇒y−x≤−b
x − y > b ⇒ y − x < − b x-y>b\Rightarrow y-x<-b x−y>b⇒y−x<−b
x − y = b ⇒ x − y ≤ b 且 x − y ≥ b x-y=b\Rightarrow x-y\leq b且x-y\geq b x−y=b⇒x−y≤b且x−y≥b(当然如果全是等式限制直接高斯消元更好)
通常差分约束可能涉及对题意进行差分/前缀和转化。
正解/负解
建最短路得出的解一定是非正解,并且是最大解。
建最长路得出的解一定是非负解,并且是最小解。
同时注意到对一组可行解的每个变量都加 k k k之后,这个解仍然是可行解,因此我们可以获得全正/全负解。
后记
于是皆大欢喜。
相关文章:

差分约束算法
差分约束 差分约束系统包含 m m m个涉及 n n n个变量的差额限制条件,这些差额限制条件每个都是形式为 x i − x j ≤ b ∈ [ 1 , m ] x_i-x_j\leq b_{\in[1,m]} xi−xj≤b∈[1,m]的简单线性不等式。 通常我们要求解出一组可行解。 最短路差分约束 如果我们…...
彻底解决vue-video-player播放视频有黑边
需求 最近需要接入海康视频摄像头,然后把视频的画面接入到自己的网站系统中。以前对接过rtsp固定IP的显示视频,这次的不一样,没有了固定IP。海康的解决办法是,摄像头通过配置服务器到萤石云平台,然后购买企业版账号和…...

区域负责人常用的ChatGPT通用提示词模板
区域市场分析:如何分析区域市场的特点、竞争态势和客户需求? 区域销售策略制定:如何制定针对区域市场的销售策略,包括产品定位、价格策略、渠道策略等? 区域销售目标设定:如何设定明确的区域销售目标&…...

Java Spring boot 可變參數,以及弊端
function中 不固定的參數 public boolean sendEmail(String manFrom, String manTo,String manCc, String subject, String... msg); 必須是最後一個參數,傳值時可以多個。 sendEmail(“a.gmail”,"b.gmail","c.gmail","subject",…...

机器视觉系统选型-线阵工业相机选型
线阵相机特点: 1.线阵相机使用的线扫描传感器通常只有一行感光单元(少数彩色线阵使用三行感光单元的传感器) 2.线阵相机每次只采集一行图像; 3.线阵相机每次只输出一行图像; 4.与传统的面阵相机相比,面阵扫…...
单机开机无感全自动进入B\S架构系统
单机开机无感全自动进入B\S架构系统 标题:单机用jar包启动项目bat(批处理)不弹黑窗口,并设置开机自启,打开浏览器,访问系统。引言:在实际工作中,遇到单机部署的情况,如今…...

大一,如何成为一名fpga工程师?
1、数电(必须掌握的基础),然后进阶学模电(选学), 2、掌握HDL(HDLverilogVHDL)可以选择verilog或者VHDL,建议verilog就行。 3、掌握FPGA设计流程/原理(推…...
MyBatisPlus学习三:Service接口、代码生成器
学习教程 黑马程序员最新MybatisPlus全套视频教程,4小时快速精通mybatis-plus框架 Service接口 简介 在MyBatis-Plus框架中,Service接口的作用是为实体类提供一系列的通用CRUD(增删改查)操作方法。通常情况下,Servi…...

产品经理如何选择城市?
年底,全国性的人口大迁徙即将开始。选择城市,堪称年轻人的“二次投胎”,族望留原籍,家贫走他乡。 古人在选择城市时,主要的考量因素是家族势力,这一点放在当代,大致也成立,如果在老…...
再谈“敏捷”与“瀑布”在产品开发过程中的反思
作为一家专注于软件开发的公司《智创有术》,我们致力于为客户提供创新、高效和可靠的解决方案。通过多年的经验和专业知识,我们已经在行业内建立了良好的声誉,并赢得了客户的信任和支持。 支持各种源码,网站搭建,APP&a…...
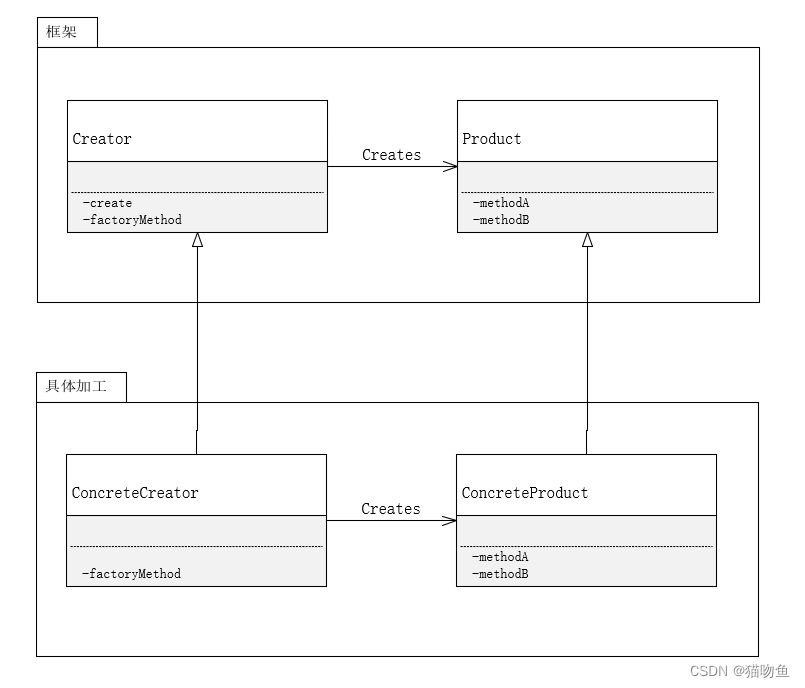
设计模式② :交给子类
文章目录 一、前言二、Template Method 模式1. 介绍2. 应用3. 总结 三、Factory Method 模式1. 介绍2. 应用3. 总结 参考内容 一、前言 有时候不想动脑子,就懒得看源码又不像浪费时间所以会看看书,但是又记不住,所以决定开始写"抄书&qu…...

Hive 源码
hive 编译 issue Failed to execute goal com.github.os72:protoc-jar-maven-plugin:3.5.1.1:run (default) on project hive-standalone-metastore: Error resolving artifact: com.google.protobuf:protoc:2.5.0: The following artifacts could not be resolved: com.goog…...
调整几行代码,接口吞吐提升 10 倍,性能调优妙啊!
景 分析过程 总结 背景 公司的一个ToB系统,因为客户使用的也不多,没啥并发要求,就一直没有经过压测。这两天来了一个“大客户”,对并发量提出了要求:核心接口与几个重点使用场景单节点吞吐量要满足最低500/s的要求。 当时一想,500/s吞吐量还不简单。Tomcat按照100个线程…...

MACOS Atrust服务异常
MAC版Atrust服务异常 点击进入办公后出现提示其一: 核心服务未启动,部分功能存在异常,确定重新启动吗? 可能的原因: 1.上次已完全退出客户端 2.核心服务被其他程序优化禁用 点击重新启动后,出现提示&#x…...
:在ChatGLM3-6B中使用langchain)
LLM大语言模型(四):在ChatGLM3-6B中使用langchain
目录 背景准备工作工具添加LangChain 已实现工具Calculator、Weather Tool配置 自定义工具自定义kuakuawo Agent 多工具使用参考 背景 LangChain是一个用于开发由语言模型驱动的应用程序的框架。它使应用程序能够: 具有上下文意识:将语言模型与上下文源(提示指令&…...
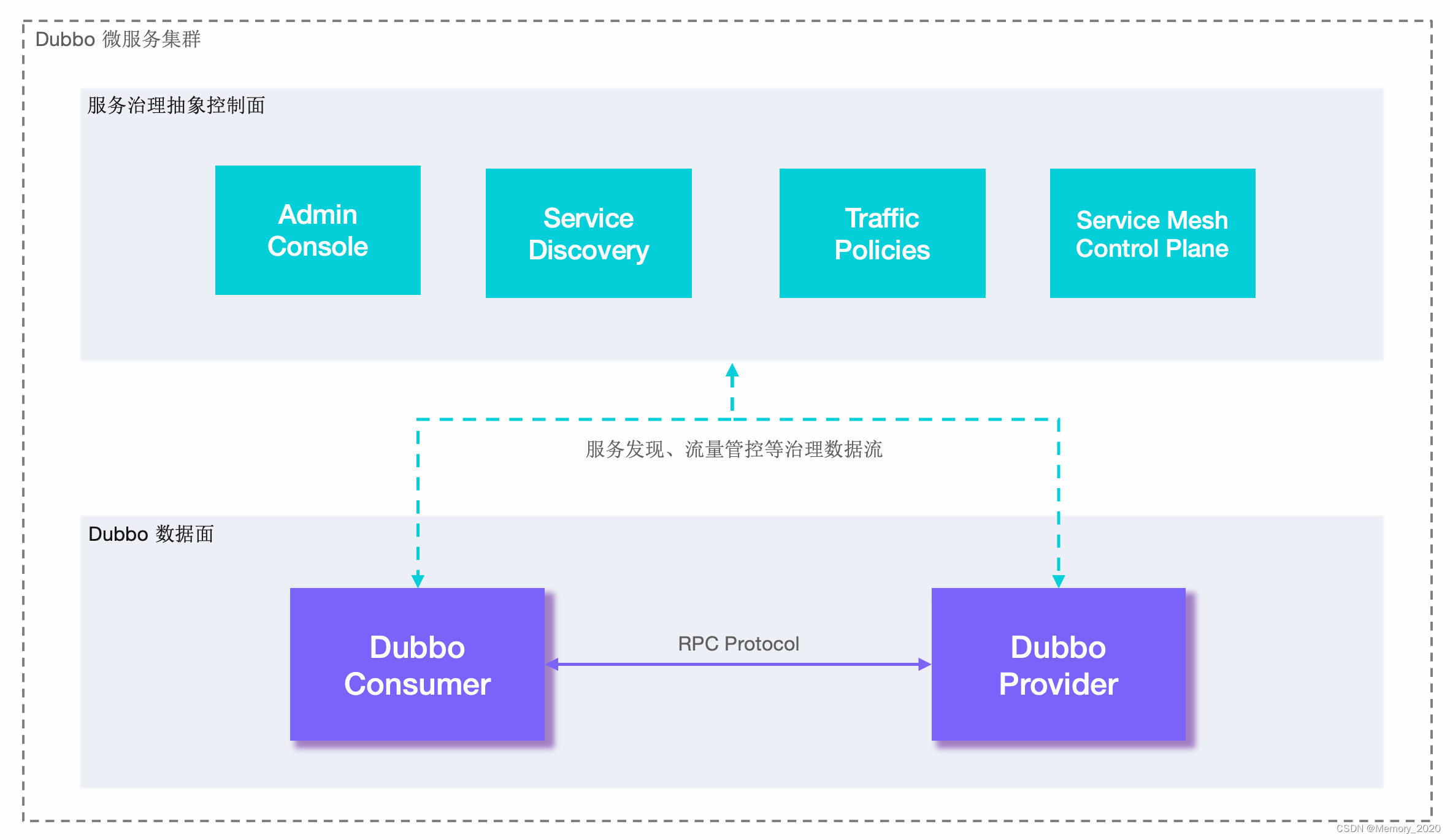
Dubbo入门介绍和实战
1. 引言 Dubbo是一款开源的高性能、轻量级的Java RPC(远程过程调用)框架,旨在解决分布式服务之间的通信问题。本文将介绍Dubbo的基础概念、核心特性以及使用场景,包括实际示例演示。 2. 什么是Dubbo? Dubbo是阿里巴…...

如何实现无人机识别功能
无人机识别算法可以基于不同的传感器和技术,结合多种方法进行实现。以下是一些常见的无人机识别算法和技术: 视觉识别: 图像处理: 使用计算机视觉技术对无人机图像进行处理,包括特征提取、目标检测和跟踪等。深度学习&…...
流程控制方法)
Python学习笔记(四)流程控制方法
流程控制有三种方法:分支、循环、跳出 流程的控制通过布尔值来实现,分支和循环都需要对一定的条件进行判断,根据判断结果(布尔值)决定下一步要做什么 布尔值通过比较运算符、逻辑运算符来进行判断是True还是False 不…...
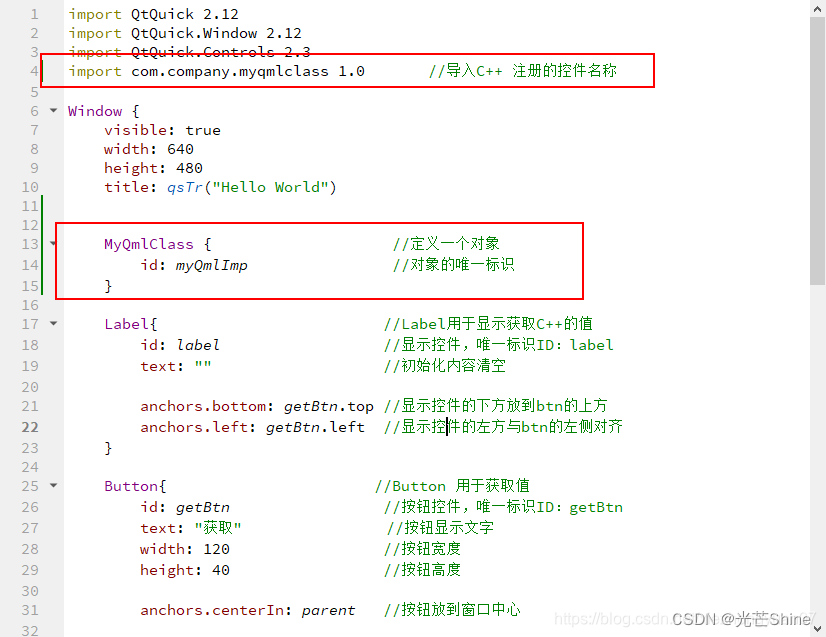
【Qt- C++ Qml 交互】
Qt编程指南 VX:hao541022348 ■ 将C对象注册到 QML中,在QML使用C对象■ C对象注册到元对象系统■ Q_INVOKABLE 宏定义是将C 的 函数(方法)声明为元对象系统可调用的函数■ 演示步骤 ■ 将 C类注册到 QML,并在QML声明一…...
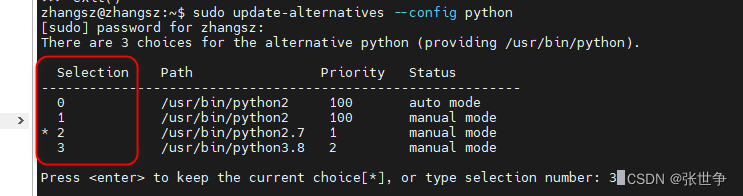
ubuntu 20.04 自由切换 python 的版本
问题描述 当前 ubuntu 20.04 默认安装了多个 python 的版本,执行 python 时,默认版本是 Python 2.7.18 zhangszzhangsz:~$ python Python 2.7.18 (default, Jul 1 2022, 12:27:04) [GCC 9.4.0] on linux2 Type "help", "copyright&quo…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
