算法29:不同路径问题(力扣62和63题)--针对算法28进行扩展
题目:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
分析:
假设为3行2列的二维数组
1. 向右---向下---向下
2. 向下---向下---向右
3. 向下--向右---向下
可以推导
1. 一直向右和一直向下,每种走法只有1种走法,没有其他可以旋转的空间。因此
| 1 | 1 |
| 1 | 2 |
| 1 |
2 、那么到达dp[1][1] 的走法就是 1 + 1 = 2;
3. 那么到达右下角dp[2][1] 就是 2 + 1 = 3; 即3种走法
分析2:
假设有3行7列
1. 按行走,只有1种走法
2、按列走,只有一种走法,可得
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | ||||||
| 1 |
那么dp[1][1] 就是 dp[0][1] + dp[1][0] 即 1+ 1 = 2;依次类推可得
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 |
第三行还是按照这种方式推导,可得
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 3 | 6 | 10 | 15 | 21 | 28 |
因此,针对3行7列的二维数组,可得28种走法
代码实现:
public int uniquePaths(int m, int n) {int[][] dp = new int[m][n];//第一行都为1for (int col = 0; col < n; col++) {dp[0][col] = 1;}//第一列都为1for (int row = 0; row < m; row++) {dp[row][0] = 1;}for (int row = 1; row < m; row++) {for(int col = 1; col < n; col++) {dp[row][col] = dp[row][col - 1] + dp[row - 1][col];}}return dp[m-1][n-1];}还是一样的问题,以上代码的时间复杂度为O(m*n), 空间复杂度也为O(m*n). 如果100行100列的二维数组,将浪费100*100的空间复杂度。
空间压缩进行优化:
public int uniquePaths2(int m, int n) {int[] dp = new int[n];//第一行都为1for (int col = 0; col < n; col++) {dp[col] = 1;}for (int row = 1; row < m; row++) {dp[0] = 1;for (int col = 1; col < n; col++) {dp[col] = dp[col -1] + dp[col];}}return dp[n -1];}完整代码:
package code03.动态规划_07.lesson4;//力扣62题
// https://leetcode.cn/problems/unique-paths/description/
public class DiffPathSum_02 {public int uniquePaths(int m, int n) {int[][] dp = new int[m][n];//第一行都为1for (int col = 0; col < n; col++) {dp[0][col] = 1;}//第一列都为1for (int row = 0; row < m; row++) {dp[row][0] = 1;}for (int row = 1; row < m; row++) {for(int col = 1; col < n; col++) {dp[row][col] = dp[row][col - 1] + dp[row - 1][col];}}return dp[m-1][n-1];}public int uniquePaths2(int m, int n) {int[] dp = new int[n];//第一行都为1for (int col = 0; col < n; col++) {dp[col] = 1;}for (int row = 1; row < m; row++) {dp[0] = 1;for (int col = 1; col < n; col++) {dp[col] = dp[col -1] + dp[col];}}return dp[n -1];}
}
力扣测试通过:
题目:力扣63题: 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
分析:
1. 这一题其实跟上面一体解法相同,唯一的不同之处是有障碍物。
2. 第一行和第一列遇到障碍物,那么后面的路都走不通而已
3. 后面的推导,当前方格为障碍物,设置0代表走不通;如果不为0,则按照原有逻辑进行推导即可
完整代码:
package code03.动态规划_07.lesson4;//力扣63题
// https://leetcode.cn/problems/unique-paths-ii/description/
public class DiffPathSum_03 {//时间复杂度 O(m*n), 空间复杂度 O(m*n)public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;//obstacleGrid[0][0] == 1 代表左上角第一个就是障碍物//obstacleGrid[m-1][n-1] == 1 代表右下角最后一个是障碍物if (obstacleGrid == null|| obstacleGrid.length == 0|| obstacleGrid[0][0] == 1|| obstacleGrid[m-1][n-1] == 1) {return 0;}int[][] dp = new int[m][n];//处理第一行dp[0][0] = 1;for (int col = 1; col < n; col++) {//如果当前列为1, 或者前一列为0. 代表遇到障碍物。后面路走不通,全部变为0if (obstacleGrid[0][col] == 1 || dp[0][col -1] == 0) {dp[0][col] = 0;} else {//第一行只有1条路dp[0][col] = 1;}}//处理第一列for (int row = 1; row < m; row++) {//如果当前列为1, 或者上一列为0. 代表遇到障碍物。后面路走不通,全部变为0if (obstacleGrid[row][0] == 1 || dp[row-1][0] == 0) {dp[row][0] = 0;} else {//第一行只有1条路dp[row][0] = 1;}}for (int row = 1; row < m; row++) {for(int col = 1; col < n; col++) {//如果当前列有障碍物,此条路走不通。当前列的值变为0//否则,按照原有的逻辑进行计算dp[row][col] = obstacleGrid[row][col] == 1 ? 0: dp[row][col - 1] + dp[row - 1][col];}}return dp[m-1][n-1];}//空间压缩//时间复杂度 O(m*n), 空间复杂度 O(n)public int uniquePathsWithObstacles2(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;//obstacleGrid[0][0] == 1 代表左上角第一个就是障碍物//obstacleGrid[m-1][n-1] == 1 代表右下角最后一个是障碍物if (obstacleGrid == null|| obstacleGrid.length == 0|| obstacleGrid[0][0] == 1|| obstacleGrid[m-1][n-1] == 1) {return 0;}int[] dp = new int[n];//处理第一行dp[0] = 1;for (int col = 1; col < n; col++) {//如果当前列为1, 或者前一列为0. 代表遇到障碍物。后面路走不通,全部变为0if (obstacleGrid[0][col] == 1 || dp[col -1] == 0) {dp[col] = 0;} else {//第一行只有1条路dp[col] = 1;}}for (int row = 1; row < m; row++) {//当前列为障碍物或者上一列为障碍物,都走不通。dp[0] = (obstacleGrid[row][0] == 1 || dp[0] == 0) ? 0 : 1;for(int col = 1; col < n; col++) {//如果当前列有障碍物,此条路走不通。当前列的值变为0//否则,按照原有的逻辑进行计算dp[col] = obstacleGrid[row][col] == 1 ? 0 : dp[col -1] + dp[col];}}return dp[n-1];}public static void main(String[] args) {DiffPathSum_03 test = new DiffPathSum_03();int[][] arr = {{0, 0, 0},{0, 1, 0},{0, 0, 0}};System.out.println(test.uniquePathsWithObstacles2(arr));}
}
相关文章:

算法29:不同路径问题(力扣62和63题)--针对算法28进行扩展
题目:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角࿰…...

openGauss学习笔记-188 openGauss 数据库运维-常见故障定位案例-core问题定位
文章目录 openGauss学习笔记-188 openGauss 数据库运维-常见故障定位案例-core问题定位188.1 磁盘满故障引起的core问题188.1.1 问题现象188.1.2 原因分析188.1.3 处理办法 188.2 GUC参数log_directory设置不正确引起的core问题188.2.1 问题现象188.2.2 原因分析188.2.3 处理办…...

kubernetes入门到进阶(5)
目录 镜像仓库:怎么用好docker hub这个宝藏 什么是镜像仓库(Registry) 什么是docker hub 如何在docker hub上挑选镜像 docker hub上进行概念股命名规则是什么 该怎么上传自己的镜像 离线环境该怎么办 小结 镜像仓库:怎么用好docke…...
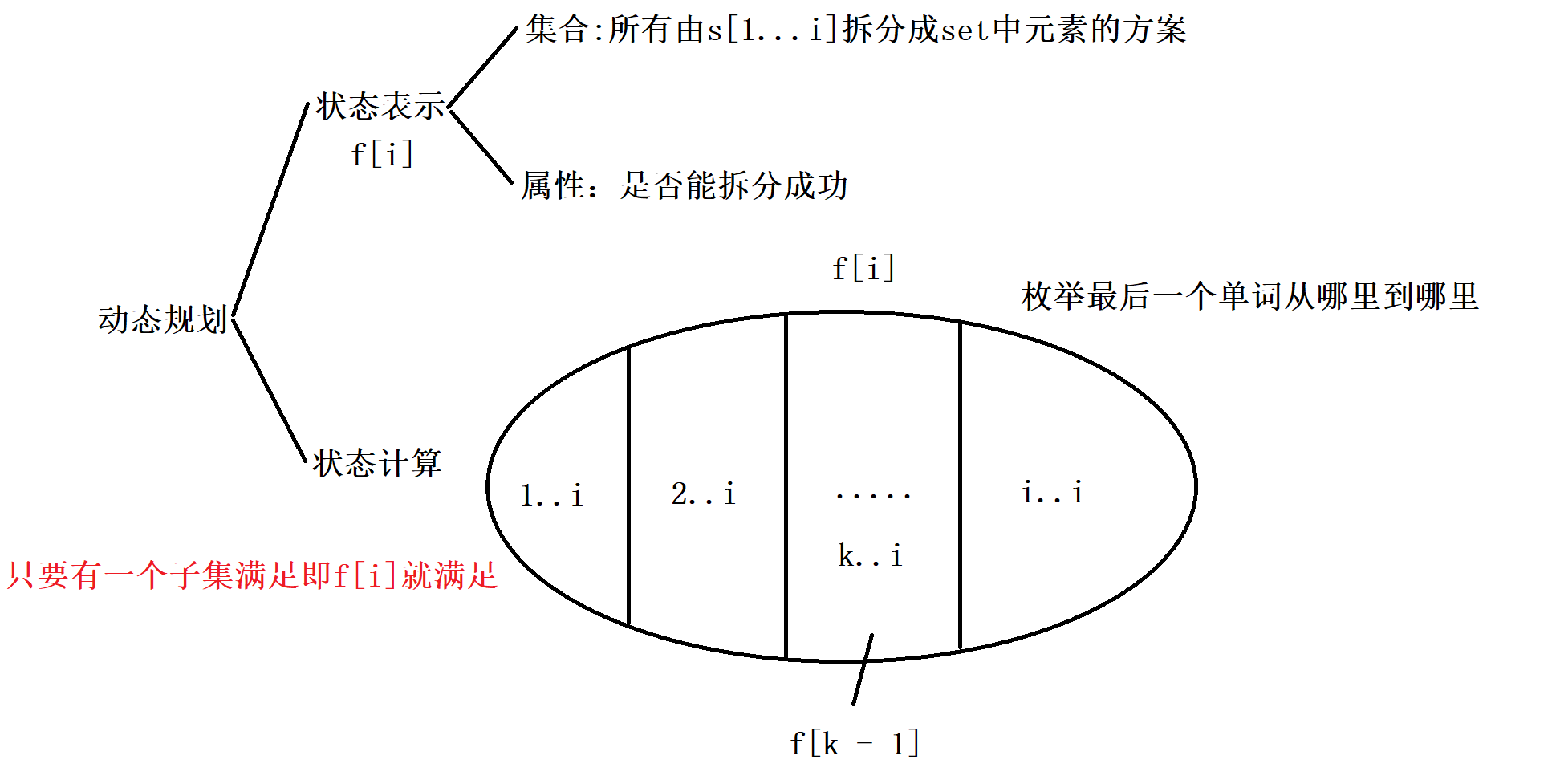
【字典树Trie】LeetCode-139. 单词拆分
139. 单词拆分。 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。 注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。 示例 1: 输入: s "leetcode&q…...

pytest常用的第三方插件介绍
本节介绍了如何安装和使用第三方插件。如果你想要编写自己的插件,请参阅“编写插件”。 通过pip可以轻松安装第三方插件: pip install pytest-NAME pip uninstall pytest-NAME如果已经安装了插件,pytest会自动找到并集成它,无需手…...
【经验】VSCode连接远程服务器(可以使用git管理、方便查看和编辑Linux源码)
1、查看OpenSSH Windows10通常自带OpenSSH不需要安装。 Windows10下检查是否已经安装OpenSSH的方法: 1)按下快捷键Win + X,选择Windows PoweShell(管理员) 2)输入以下指令: Get-WindowsCapability -Online | ? Name -like ‘OpenSSH*’ 3)如果电脑未安装OpenSSH,…...

机器学习-生存分析:如何基于随机生存森林训练乳腺癌风险评估模型?
一、 引言 乳腺癌是女性最常见的恶性肿瘤之一,也是全球范围内女性死亡率最高的癌症之一。据统计,每年全球有超过200万人被诊断为乳腺癌,其中约60万人死于该疾病。因此,乳腺癌的早期诊断和风险评估对于预防和治疗乳腺癌具有非常重要…...

MySQL学习笔记1: 数据库的简单介绍
目录 1. 数据库是什么2. 数据库这一类软件中的一些典型代表2.1. Oracle2.2. MySQL2.3. SQL Server2.4. SQLite (lite 轻量版) 3. 数据库的类型3.1. 关系型数据库3.2. 非关系型数据库 4. 总结 1. 数据库是什么 数据库是一类软件,这一类软件可以用来管理数据…...
)
【Docker】安装ELK(Docker Compose)
一、创建挂载目录 mkdir -p /docker/elk/elasticsearch/{plugins,data} mkdir -p /docker/elk/logstash 二、给目录授权 chmod 777 /docker/elk/elasticsearch/data 创建logstash配置文件 vim /docker/elk/logstash/logstash.conf input {tcp {mode => "server" h…...

【机器学习:欧氏距离 】机器学习中欧氏距离的理解和应用
【机器学习:欧氏距离 】机器学习中欧氏距离的理解和应用 距离公式二维更高的维度点以外的物体属性欧几里得距离的平方概括历史 在数学中,欧氏距离’是指欧氏空间中任意两点之间的直线距离。这种距离可以通过应用勾股定理来计算,利用两点的笛卡…...

系统安全及应用
1、基本安全措施 1.1、系统账号清理 在Linux系统中,除了用户手动创建的各种账号之外,还包括随系统或程序安装过程而生产的其他大量账号。除了超级用户root之外,其他大量账号只是用来维护系统运作、启动或保持服务进程,一般是不允…...

Danil Pristupov Fork(强大而易用的Git客户端) for Mac/Windows
在当今软件开发领域,团队协作和版本控制是非常重要的方面。在这个过程中,Git成为了最受欢迎的版本控制工具之一。然而,对于Git的使用,一个好的客户端是至关重要的。 今天,我们要为大家介绍一款强大而易用的Git客户端—…...
最新GPT4.0使用教程,AI绘画,ChatFile文档对话总结+GPT语音对话使用,DALL-E3文生图
一、前言 ChatGPT3.5、GPT4.0、GPT语音对话、Midjourney绘画,文档对话总结DALL-E3文生图,相信对大家应该不感到陌生吧?简单来说,GPT-4技术比之前的GPT-3.5相对来说更加智能,会根据用户的要求生成多种内容甚至也可以和…...

【ARM 嵌入式 编译系列 7.2 -- GCC 链接脚本中 DEFINED 函数与 “AT>“ 符号详细介绍】
文章目录 GCC 链接脚本中 DEFINED 函数DEFINED() 函数> (放置在哪个区域)AT> (加载地址) (填充字节) 在链接脚本中,组合示例 GCC 链接脚本中 DEFINED 函数 在 ARM GCC 链接脚本(.ld 文件)中,DEFINED() 是一种内置函数&…...
Linux基础——进程初识(二)
1. 对当前目录创建文件的理解 我们知道在创建一个文件时,它会被默认创建到当前目录下,那么它是如何知道当前目录的呢? 对于下面这样一段代码 #include <stdio.h> #include <unistd.h>int main() {fopen("tmp.txt", …...

国科大图像处理2024速通期末——汇总2017-2019、2023回忆
国科大2023.12.28图像处理0854期末重点 图像处理 王伟强 作业 课件 资料 一、填空 一个阴极射线管它的输入与输出满足 s r 2 sr^{2} sr2,这将使得显示系统产生比希望的效果更暗的图像,此时伽马校正通常在信号进入显示器前被进行预处理,令p…...
)
编程笔记 html5cssjs 026 HTML输入类型(2/2)
编程笔记 html5&css&js 026 HTML输入类型(2/2) 输入类型:date输入类型:color输入类型:range输入类型:month输入类型:week输入类型:time输入类型:datetime输入类型…...
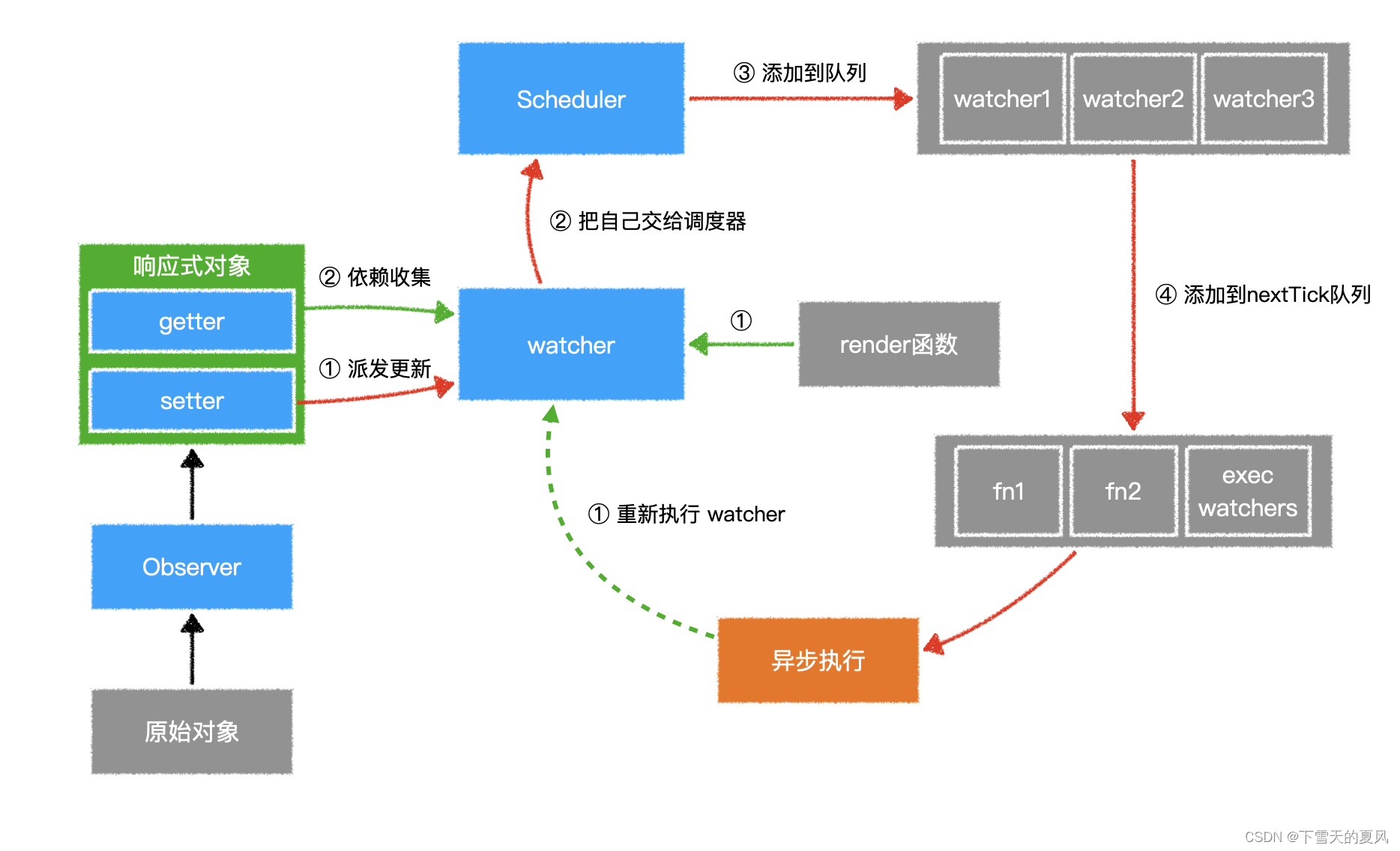
Vue2 - 数据响应式原理
目录 1,总览2,Observer3,Dep4,Watcher5,Schedule 1,总览 vue2官网参考 简单介绍下上图流程:以 Data 为中心来说, Vue 会将传递给 Vue 实例的 data 选项(普通 js 对象&a…...

基于华为云解析服务实现网站区域封禁
前言 中国大陆以外的网络攻击不断,个人博客时常遭受不明个人或组织的攻击,给网站的安全运行带来了巨大的风险,同时DDoS、CC攻击等还会消耗服务器的资源,站长可能需要因此支付高昂的服务器、CDN的流量费用。 因此,如果…...

在 Docker 中配置 MySQL 数据库并初始化 Project 项目
1. 文件准备 1.1. 添加 SQL 文件头部内容 每个 SQL 文件的头部需要添加以下内容: DROP DATABASE IF EXISTS xx_..; CREATE DATABASE xx_..; USE xx_..;1.2. 修改 AUTO_INCREMENT 在每个 SQL 文件中,将 AUTO_INCREMENT 修改为 1。 1.3. 插入机型 在 SQL…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...
