【算法系列 | 12】深入解析查找算法之—斐波那契查找

序言
心若有阳光,你便会看见这个世界有那么多美好值得期待和向往。
决定开一个算法专栏,希望能帮助大家很好的了解算法。主要深入解析每个算法,从概念到示例。
我们一起努力,成为更好的自己!
今天第12讲,讲一下查找算法的—斐波那契查找
一、算法介绍
斐波那契查找算法是一种基于黄金分割的有序查找算法,通过斐波那契数列的特性,在有序序列中快速定位目标元素的位置。
1.1 原理介绍
它结合了二分查找和黄金分割的思想。这个算法的基本原理如下:
序列构建: 首先,需要一个有序的数组或序列。这个数组的长度通常是斐波那契数列中的一个值,这有助于在查找过程中对数组进行分割。
斐波那契数列: 斐波那契数列是一组按以下递归关系定义的数字序列:F(0) = 0,F(1) = 1,F(n) = F(n-1) + F(n-2)(n > 1)。通常,斐波那契数列的前几项是:0, 1, 1, 2, 3, 5, 8, 13, 21, ...
查找过程: 对于一个有序序列,首先选择一个斐波那契数列中的值,使得这个值大于或等于待查找序列的长度,然后使用这个斐波那契数列的值将序列分成两个部分。这两个部分的长度之比就是相邻两个斐波那契数的比例。
比较: 比较要查找的元素与序列中分割点的元素。如果相等,则找到了目标元素;如果待查找元素小于分割点元素,继续在前半部分进行查找;如果待查找元素大于分割点元素,继续在后半部分进行查找。
迭代: 重复上述步骤,不断缩小查找范围,直到找到目标元素或确定元素不在序列中。
示例说明
假设有一个有序数组
arr,长度为 n,而 n 正好是斐波那契数列中的某个值。为了简化,我们可以选择 n 为斐波那契数列中的某个值,比如 F(5) = 5,所以 n = 5。那么,我们有一个有序数组arr,长度为 5。
arr = [1, 3, 5, 7, 9]
接下来,我们要查找值为 5 的元素在数组中的位置。以下是斐波那契查找的步骤:
1. 选择斐波那契数列的值: 在斐波那契数列中找到一个最小的值,使得 F(k) >= n,其中 k 是最小可能满足的索引。在这个例子中,我们选择 F(5) = 5。
2. 分割数组: 将数组分成两个部分,长度比例为斐波那契数列中的两个相邻值的比例。在这个例子中,我们有两部分,长度比例是 3:2。
arr_left = [1, 3, 5] arr_right = [7, 9]
3. 比较与查找: 比较要查找的元素(5)与分割点元素(arr[2] = 5)。如果相等,找到了目标元素。如果待查找元素小于分割点元素,继续在前半部分进行查找。如果待查找元素大于分割点元素,继续在后半部分进行查找。
在这个例子中,5 等于分割点元素,所以我们找到了目标元素的位置。
4. 迭代: 重复上述步骤,直到找到目标元素或确定元素不在序列中。
1.2 优缺点
优点:
适用性广泛: 斐波那契查找适用于有序序列,尤其在序列长度接近斐波那契数列的某个值时效果更佳。相较于二分查找,斐波那契查找能够在某些特定情况下减少查找次数。
更好的平衡: 由于斐波那契查找使用黄金分割比例进行分割,使得分割后的两个子序列的长度比例更加接近,有助于保持查找的平衡性。
相对均匀的分割: 斐波那契查找相对于其他分割方法,如二分查找,能够产生更为均匀的分割,有助于在查找过程中更快地接近目标元素。
缺点:
数组长度限制: 斐波那契查找要求待查找的序列长度必须是斐波那契数列中的某个值,这在实际应用中可能不太灵活,特别是当数据规模不是恰好是斐波那契数列中的某个值时,可能需要对数据进行补齐。
比较次数不稳定: 斐波那契查找在某些情况下可能会比二分查找效果更好,但并不是在所有情况下都表现更好。具体的性能取决于待查找数据的分布情况和序列的长度。在一些场景下,二分查找可能更为稳定。
计算斐波那契数列: 为了选择合适的斐波那契数列的值,需要事先计算斐波那契数列,这可能涉及到一些计算成本,特别是对于较大的数据集。
总体来说,斐波那契查找算法在某些特定条件下表现优秀,但在实际应用中需要谨慎选择,并根据具体情况考虑使用。在一些情况下,简单的二分查找可能更加实用和高效。
1.3 复杂度
时间复杂度:
查找过程: 斐波那契查找的主要操作是不断地缩小查找范围,通过比较待查找元素与分割点元素来确定继续在前半部分还是后半部分进行查找。在每一步操作中,都可以将待查找范围缩小为原来的黄金分割比例,即约为 0.618。
时间复杂度: 斐波那契查找的时间复杂度可以表示为 O(log n),其中 n 是待查找序列的长度。与二分查找相比,它的复杂度相对更低。
空间复杂度:
常数空间: 斐波那契查找算法的空间复杂度非常低。它只需要常数级别的额外空间来存储一些中间变量,如斐波那契数列的值、分割点等。
O(1): 因此,斐波那契查找的空间复杂度可以表示为 O(1)。
总体来说,斐波那契查找在时间复杂度和空间复杂度上都相对较低,这使得它在某些特定场景下成为一个有效的查找算法。
但需要注意,实际效果还受到数据分布等因素的影响,因此在选择查找算法时,需要综合考虑具体情况。
1.4 使用场景
斐波那契查找算法在一些特定的场景下表现良好,适用于如下情况:
有序序列: 斐波那契查找要求待查找的序列是有序的,因为它是基于比较来缩小查找范围的。如果序列无序,需要先进行排序操作。
长度接近斐波那契数: 算法对序列的长度有一定的要求,最好是恰好是斐波那契数列中的某个值。在实际应用中,可以选择最接近并大于待查找序列长度的斐波那契数。
分布均匀: 如果数据在序列中的分布相对均匀,斐波那契查找可以更好地发挥其优势。这是因为它能够在分割序列时保持更好的平衡。
查找频繁但数据变动不频繁: 如果对同一序列进行多次查找而且序列基本保持不变,斐波那契查找的一些前期计算可以提前完成,然后多次使用相同的计算结果进行查找,从而提高效率。
适用于内存有限的情况: 斐波那契查找只需要常数级别的额外空间,因此在内存有限的情况下比一些其他算法更为适用。
需要注意的是,斐波那契查找并不总是比其他查找算法更好,它在特定的条件下才会表现出色。在实际应用中,需要根据具体情况选择最适合的查找算法。
二、代码实现
2.1 Java代码实现
2.1.1 代码示例
public class FibonacciSearch {// 辅助函数:生成斐波那契数列private static int[] generateFibonacci(int n) {int[] fibonacci = new int[n];fibonacci[0] = 0;fibonacci[1] = 1;for (int i = 2; i < n; i++) {fibonacci[i] = fibonacci[i - 1] + fibonacci[i - 2];}return fibonacci;}// 斐波那契查找算法public static int fibonacciSearch(int[] arr, int key) {int n = arr.length;// 生成斐波那契数列,找到最接近且大于等于 n 的值int[] fibonacci = generateFibonacci(n);int k = 0;while (fibonacci[k] < n) {k++;}// 将数组扩展到斐波那契数列的长度int[] temp = new int[fibonacci[k]];System.arraycopy(arr, 0, temp, 0, n);int low = 0;int high = n - 1;// 主要查找过程while (low <= high) {int mid = low + fibonacci[k - 1] - 1;if (key < temp[mid]) {high = mid - 1;k -= 1;} else if (key > temp[mid]) {low = mid + 1;k -= 2;} else {// 找到了目标元素,需要判断返回的是原数组中的索引还是扩展数组中的索引return Math.min(mid, high);}}// 未找到目标元素return -1;}public static void main(String[] args) {int[] arr = {1, 3, 5, 7, 9, 11, 13, 15};int key = 7;int result = fibonacciSearch(arr, key);if (result != -1) {System.out.println("元素 " + key + " 在数组中的索引为:" + result);} else {System.out.println("元素 " + key + " 不在数组中");}}
}
2.1.2 代码详解
generateFibonacci方法:生成斐波那契数列,参数n表示生成数列的长度。
fibonacciSearch方法:实现了斐波那契查找算法。首先,通过调用generateFibonacci方法生成斐波那契数列,然后找到最接近并大于等于数组长度的斐波那契数。接着,将原数组扩展到斐波那契数列的长度,再进行主要的查找过程。查找过程中,根据比较的结果不断缩小查找范围,直到找到目标元素或确定元素不在序列中。
main方法:在这里,创建一个有序数组arr,并调用fibonacciSearch方法查找元素 7 的索引。最后,输出查找结果。
2.1.3 运行结果
元素 7 在数组中的索引为:32.2 Python代码实现
2.2.1 代码示例
def generate_fibonacci(n):"""生成斐波那契数列"""fibonacci = [0, 1]while fibonacci[-1] < n:fibonacci.append(fibonacci[-1] + fibonacci[-2])return fibonaccidef fibonacci_search(arr, key):"""斐波那契查找算法"""n = len(arr)# 生成斐波那契数列,找到最接近且大于等于 n 的值fibonacci = generate_fibonacci(n)k = 0while fibonacci[k] < n:k += 1# 将数组扩展到斐波那契数列的长度temp = arr + [arr[-1]] * (fibonacci[k] - n)low, high = 0, n - 1# 主要查找过程while low <= high:mid = low + fibonacci[k - 1] - 1if key < temp[mid]:high = mid - 1k -= 1elif key > temp[mid]:low = mid + 1k -= 2else:# 找到了目标元素,返回原数组中的索引return min(mid, n - 1)# 未找到目标元素return -1if __name__ == '__main__':# 测试arr = [1, 3, 5, 7, 9, 11, 13, 15]key = 7result = fibonacci_search(arr, key)if result != -1:print(f"元素 {key} 在数组中的索引为:{result}")else:print(f"元素 {key} 不在数组中")2.2.2 代码详解
generate_fibonacci函数:用于生成斐波那契数列,直到数列的最后一个值大于等于给定的参数n。
fibonacci_search函数:实现了斐波那契查找算法。首先,调用generate_fibonacci函数生成斐波那契数列,然后找到最接近并大于等于数组长度的斐波那契数。接着,将原数组扩展到斐波那契数列的长度,再进行主要的查找过程。查找过程中,根据比较的结果不断缩小查找范围,直到找到目标元素或确定元素不在序列中。
在测试部分,创建一个有序数组 arr,并调用 fibonacci_search 函数查找元素 7 的索引。最后,输出查找结果。
2.2.3 运行结果
元素 7 在数组中的索引为:3好啦,今天就到这里啦,下期见喽~~🙉
三、图书推荐
3.1 图书名称
图书名称:《Pandas数据分析》
Pandas是强大且流行的库,是Python中数据科学的代名词。这本书会介绍如何使用Pandas对真实世界的数据集进行数据分析,如股市数据、模拟黑客攻击的数据、天气趋势、地震数据、葡萄酒数据和天文数据等。
Pandas使我们能够有效地处理表格数据,从而使数据整理和可视化变得更容易。等不及的小伙伴,可以点击这个链接先睹为快 《Pandas数据分析》

3.2 图书介绍


3.3 参与方式
图书数量:本次送出 2 本 !!!⭐️⭐️⭐️
活动时间:截止到 2024-01-09 12:00:00抽奖方式:
- 评论区随机抽取小伙伴!
留言内容,以下方式都可以:
- 根据文章内容进行高质量评论
参与方式:关注博主、点赞、收藏,评论区留言
3.4 中奖名单
🍓🍓 获奖名单🍓🍓
中奖名单:请关注博主动态
名单公布时间:2024-01-09 下午
相关文章:

【算法系列 | 12】深入解析查找算法之—斐波那契查找
序言 心若有阳光,你便会看见这个世界有那么多美好值得期待和向往。 决定开一个算法专栏,希望能帮助大家很好的了解算法。主要深入解析每个算法,从概念到示例。 我们一起努力,成为更好的自己! 今天第12讲,讲…...

全新的C++语言
一、概述 C 的最初目标就是成为 “更好的 C”,因此新的标准首先要对基本的底层编程进行强化,能够反映当前计算机软硬件系统的最新发展和变化(例如多线程)。另一方面,C对多线程范式的支持增加了语言的复杂度࿰…...

three.js 多通道组合
效果: 代码: <template><div><el-container><el-main><div class"box-card-left"><div id"threejs" style"border: 1px solid red"></div><div style"border: 1px so…...

编程笔记 html5cssjs 022 HTML表单概要
编程笔记 html5&css&js 022 HTML表单概要 一、<form> 元素二、HTML Form 属性三、操作小结 网页光是输出没有输入可不行,因为输出还是比输入容易,所有就先接触输出,后学习输入。html用来输入的东西叫“表单”。 HTML 表单用于搜…...

三子棋(c语言)
前言: 三子棋是一种民间传统游戏,又叫九宫棋、圈圈叉叉棋、一条龙、井字棋等。游戏规则是双方对战,双方依次在9宫格棋盘上摆放棋子,率先将自己的三个棋子走成一条线就视为胜利。但因棋盘太小,三子棋在很多时候会出现和…...
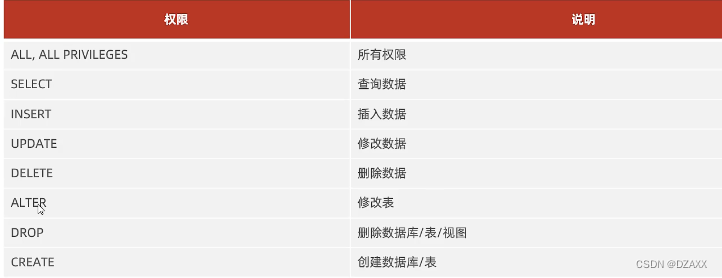
MySQL-DCL
DCL是数据控制语言,用来管理数据库用户,控制数据库的访问权限。 管理用户:管理哪些用户可以访问哪些数据库 1.查询用户 USE mysql; SELECT * FROM user; 注意: MySQL中用户信息和用户的权限信息都是记录在mysql数据库的user表中的…...

QT开源类库集合
QT开源类库集合 一、自定义控件 QSintQicsTableLongscroll-qtAdvanced Docking System 二、图表控件 QwtQCustomPlotJKQTPlotter 三、网络 QHttpEngineHTTP 四、 音视频 vlc-qt 五、多线程 tasks 六、数据库 EasyQtSql 一、自定义控件 1. QSint 源代码地址:QSint&…...
--算法(2))
C++ STL(2)--算法(2)
算法(2)----STL里的排序函数。 1. sort: 对容器或普通数组中指定范围内的元素进行排序,默认进行升序排序。 sort函数是基于快速排序实现的,属于不稳定排序。 只支持3种容器:array、vector、deque。 如果容器中存储的是自定义的对象ÿ…...
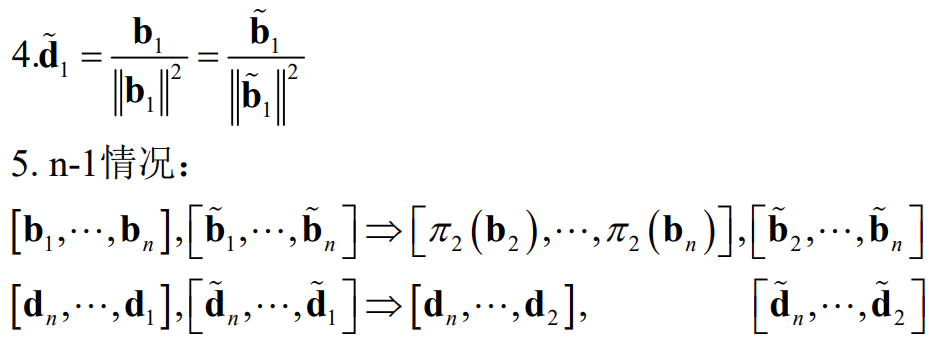
格密码基础:对偶格(超全面)
目录 一. 对偶格的格点 1.1 基本定义 1.2 对偶格的例子 1.3 对偶格的图形理解 二. 对偶格的格基 2.1 基本定义 2.2 对偶格的格基证明 三. 对偶格的行列式 3.1 满秩格 3.2 非满秩格 四. 重复对偶格 五. 对偶格的转移定理(transference theoremÿ…...

ECMAScript简介及特性
ECMAScript是一种由ECMA国际(前身为欧洲计算机制造商协会)制定和发布的脚本语言规范,JavaScript在它基础上进行了自己的封装。ECMAScript和JavaScript的关系是,前者是后者的规格,后者是前者的一种实现。 ECMAScript的…...
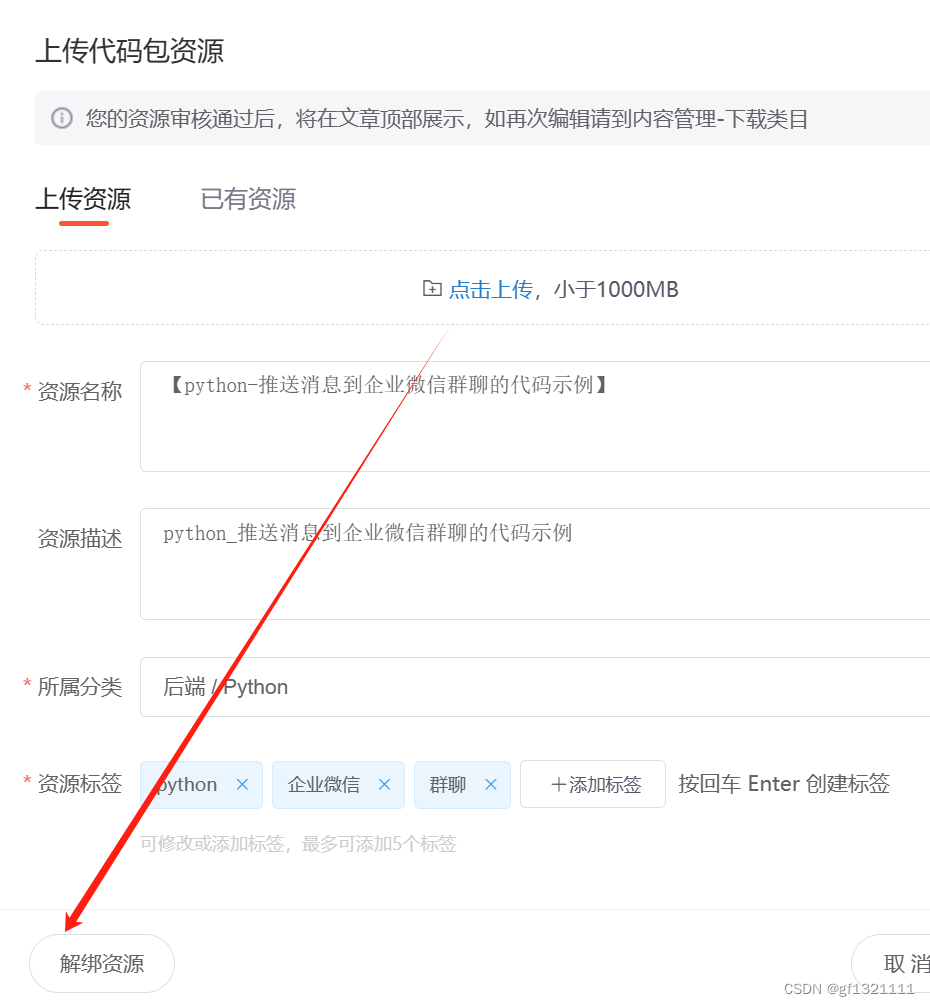
csdn中的资源文件如何删除?
csdn中的资源文件如何删除? 然后写文章的时候 点击资源绑定,解锁资源,就可以再次上传。...

NA原理及配置
在IP地址空间中,a;b;c类地址中各有一部分地址,被称为私有IP地址(私网地址),其余的为公有IP地址(公网地址) A:10.0.0.0 - 10.255.255.255 --- 相当于1条A类网段…...

解决:TypeError: ‘tuple’ object does not support item assignment
解决:TypeError: ‘tuple’ object does not support item assignment 文章目录 解决:TypeError: tuple object does not support item assignment背景报错问题报错翻译报错位置代码报错原因解决方法方法一:方法二:今天的分享就到…...
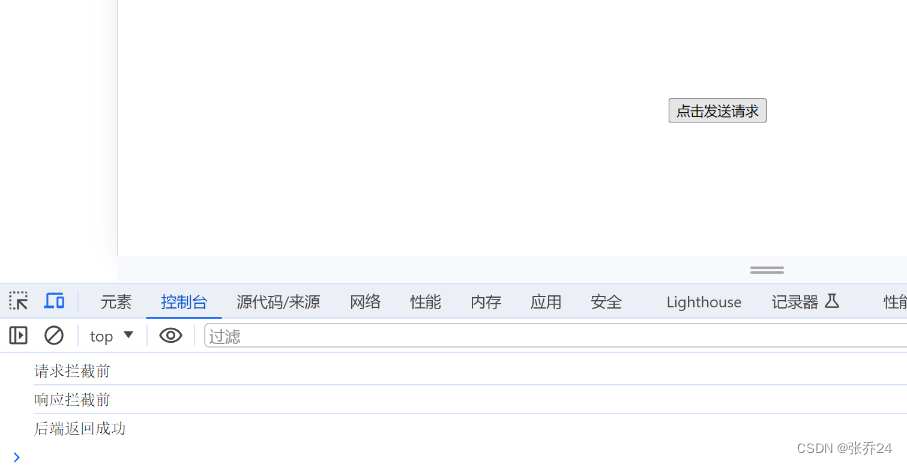
vue3项目中axios的常见用法和封装拦截(详细解释)
1、axios的简单介绍 Axios是一个基于Promise的HTTP客户端库,用于浏览器和Node.js环境中发送HTTP请求。它提供了一种简单、易用且功能丰富的方式来与后端服务器进行通信。能够发送常见的HTTP请求,并获得服务端返回的数据。 此外,Axios还提供…...

基础语法(一)(1)
常量和表达式 在这里,我们可以把Python当成一个计算器,来进行一些算术运算 例如: print(1 2 - 3) print(1 2 * 3) print(1 2 / 3)注意: print是一个python内置的函数,这个稍后我们会进行介绍 可以使用-*/&…...
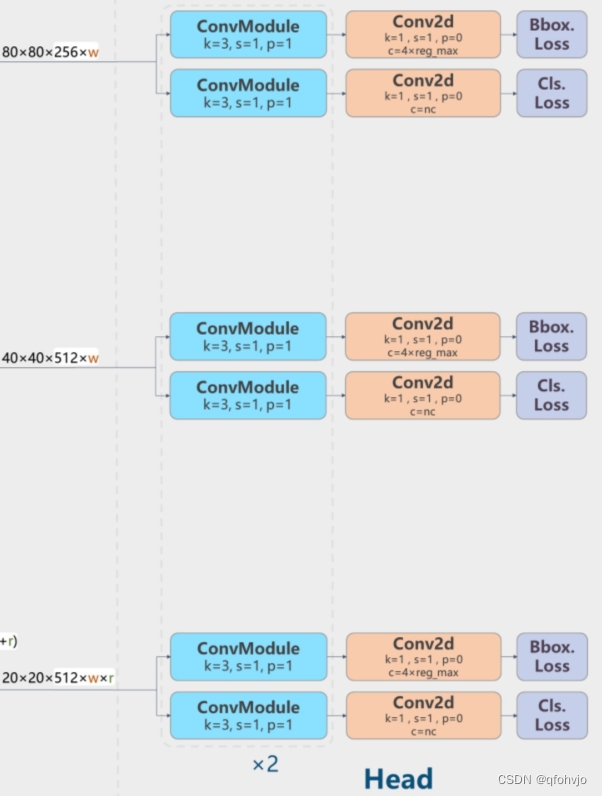
YOLOv8模型yaml结构图理解(逐层分析)
前言 YOLO-V8(官网地址):https://github.com/ultralytics/ultralytics 一、yolov8配置yaml文件 YOLOv8的配置文件定义了模型的关键参数和结构,包括类别数、模型尺寸、骨架(backbone)和头部(hea…...

【大数据】Zookeeper 集群及其选举机制
Zookeeper 集群及其选举机制 1.安装 Zookeeper 集群2.如何选取 Leader 1.安装 Zookeeper 集群 我们之前说了,Zookeeper 集群是由一个领导者(Leader)和多个追随者(Follower)组成,但这个领导者是怎么选出来的…...

Redis 过期策略
我们在set key的时候可以设置key的过期时间,哪redis是怎么处理过期的key的呢? 有三种过期策略 定时过期:每个设置过期时间的key会创建一个定时器,到过期时间就会立即对key进行清除。该策略可以立即清除过期的数据,对…...
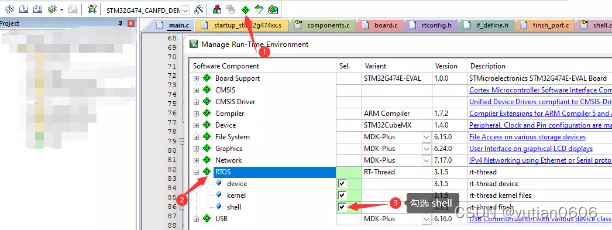
RT_Thread 调试笔记:串口打印、MSH控制台 相关
说明:记录日常使用 RT_Thread 开发时做的笔记。 持续更新中,欢迎收藏。 1.打印相关 1.打印宏定义,可以打印打印所在文件,函数,行数。 #define PRINT_TRACE() printf("-------%s:%s:%d------\r\n", __FIL…...
(适趣AI)Vue笔试题
📑前言 本文主要是【Vue】——(适趣AI)Vue笔试题的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是听风与他🥇 ☁️博客首页:CSDN主页听风与他 …...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
