吴恩达深度学习l2week2编程作业—Optimization Methods(最新中文跑通版)
到目前为止,您一直使用渐变下降来更新参数并将成本降至最低。在本笔记本中,您将获得一些更先进的优化方法的技能,这些方法可以加快学习速度,甚至可能使您获得更好的成本函数最终值。拥有一个好的优化算法可能是等待几天与只需几个小时就能获得好结果的区别。
到此笔记本结束时,您将能够:
- 运用优化算法例如Gradient Descent,Momentum,RMSprop,Adam
- 使用随机迷你批次加速收敛并改进优化
梯度下降在成本函数𝐽上“走下坡路”。可以将其视为尝试这样做:

在训练的每一步,你都会按照特定的方向更新你的参数,试图达到尽可能低的点。
![]()
让我们跟着吴恩达大佬的步伐开始吧!
1.导入packages
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasetsfrom opt_utils_v1a import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils_v1a import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from copy import deepcopy
from testCases import *
from public_tests import *%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'%load_ext autoreload
%autoreload 22.梯度下降Gradient Descent
机器学习中一种简单的优化方法是梯度下降(GD)。我们每一次循环都是对整个训练集进行学习,这叫做批量梯度下降(Batch Gradient Descent),我们之前说过了最核心的参数更新的公式,这里我们再来看一下:

L是层数 ;𝛼是学习率
Exercise 1 - update_parameters_with_gd
def update_parameters_with_gd(parameters, grads, learning_rate):
"""
parameters——包含要更新的参数的python字典:
parameters['W'+str(l)]=Wl
parameters['b'+str(l)]=bl
grades——包含梯度的python字典,用于更新每个参数:
梯度['dW'+str(l)]=dWl
梯度['db'+str(l)]=dbl
learning_rate——学习速率,标量。
返回parameters——包含更新参数的python字典
"""for l in range(L):parameters["W" + str(l +1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]parameters["b" + str(l +1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]return parametersparameters, grads, learning_rate = update_parameters_with_gd_test_case()
learning_rate = 0.01
parameters = update_parameters_with_gd(parameters, grads, learning_rate)print("W1 =\n" + str(parameters["W1"]))
print("b1 =\n" + str(parameters["b1"]))
print("W2 =\n" + str(parameters["W2"]))
print("b2 =\n" + str(parameters["b2"]))update_parameters_with_gd_test(update_parameters_with_gd)
其中的一个变体是随机梯度下降(SGD),它相当于小批量梯度下降,其中每个小批量只有一个例子。您刚刚实现的更新规则不会更改。改变的是,一次只计算一个训练示例的梯度,而不是整个训练集的梯度。下面的代码示例说明了随机梯度下降和批量梯度下降之间的区别。
- 批量梯度下降
X = data_input
Y = labels
m = X.shape[1] # Number of training examples
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):# Forward propagationa, caches = forward_propagation(X, parameters)# Compute costcost_total = compute_cost(a, Y) # Cost for m training examples# Backward propagationgrads = backward_propagation(a, caches, parameters)# Update parametersparameters = update_parameters(parameters, grads)# Compute average costcost_avg = cost_total / m- 随机梯度下降
X = data_input
Y = labels
m = X.shape[1] # Number of training examples
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):cost_total = 0for j in range(0, m):# Forward propagationa, caches = forward_propagation(X[:,j], parameters)# Compute costcost_total += compute_cost(a, Y[:,j]) # Cost for one training example# Backward propagationgrads = backward_propagation(a, caches, parameters)# Update parametersparameters = update_parameters(parameters, grads)# Compute average costcost_avg = cost_total / m在随机梯度下降算法中,每次迭代中仅使用其中一个样本,当训练集很大时,使用随机梯度下降算法的运行速度会很快,但是会存在一定的波动。
在随机梯度下降中,在更新梯度之前,只使用1个训练样本。 当训练集较大时,随机梯度下降可以更快,但是参数会向最小值摆动,而不是平稳地收敛,我们来看一下比较图:
还要注意,实现SGD总共需要3个for循环:
- 遍历迭代次数
- 遍历m个训练样本
- 遍历层数
在实际中,更好的方法是使用小批量(mini-batch)梯度下降法,小批量梯度下降法是一种综合了梯度下降法和随机梯度下降法的方法,在它的每次迭代中,既不是选择全部的数据来学习,也不是选择一个样本来学习,而是把所有的数据集分割为一小块一小块的来学习,它会随机选择一小块(mini-batch),块大小一般为。一方面,充分利用的GPU的并行性,更一方面,不会让计算时间特别长,来看一下比较图:

3.Mini-Batch梯度下降
使用mini-batch要经过两个步骤:
- 把训练集打乱,但是X和Y依旧是一一对应的,之后,X的第i列是与Y中的第i个标签对应的样本。乱序步骤确保将样本被随机分成不同的小批次。如下图,X和Y的每一列代表一个样本
- 切分,我们把训练集打乱之后,我们就可以对它进行切分了。这里切分的大小是64,如下图:


Exercise 2 - random_mini_batches
实施random_mini_batches
#经历完打乱,分割后
#第一个mini-batch
first_mini_batch_X = shuffled_X[:, 0 : mini_batch_size]
#第二个mini-batch
second_mini_batch_X = shuffled_X[:, mini_batch_size : 2 * mini_batch_size]
...
...请注意,最后一个小批量最终可能小于mini_batch_size=64。
让⌊𝑠⌋ 表示s向下取整到最接近的整数(这是Python中的math.floor(s))。如果示例的总数不是mini_batch_size=64的倍数,则将存在⌊⌋
完整64个实例的小批量,最终小批量中的实例数量为⌊m - mini_batch_size* ⌊⌋⌋

使用for循环变量k可以帮助以mini_batch_size的倍数递增i和j。
例如,如果要以3的倍数递增,可以执行以下操作:
n = 3
for k in (0 , 5):print(k * n)# GRADED FUNCTION: random_mini_batchesdef random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
"""
从(X,Y)中创建一个随机的mini-batch列表
X - 输入数据,维度为(输入节点数量,样本的数量)
Y - 对应的是X的标签(1对应蓝点|0对应红点),维度为(1,样本的数量)
mini_batch_size - 每个mini-batch的样本数量
返回
mini-bacthes - 一个同步列表,维度为(mini_batch_X,mini_batch_Y)
"""np.random.seed(seed) m = X.shape[1] # 训练样本数mini_batches = []#第一步:打乱顺序permutation = list(np.random.permutation(m)) #它会返回一个长度为m的随机数组,且里面的数是0到m-1shuffled_X = X[:,permutation] #将每一列的数据按permutation的顺序来重新排列。shuffled_Y = Y[:,permutation].reshape((1,m))inc = mini_batch_size#第二步,分割#仅具有完整小批量大小的案例,即64个实例中的每一个。num_complete_minibatches = math.floor(m / mini_batch_size) #把你的训练集分割成多少份,请注意,如果值是99.99,那么返回值是99,剩下的0.99会被舍弃for k in range(0,num_complete_minibatches):mini_batch_X = shuffled_X[:,k * mini_batch_size:(k+1)*mini_batch_size]mini_batch_Y = shuffled_Y[:,k * mini_batch_size:(k+1)*mini_batch_size]mini_batch = (mini_batch_X, mini_batch_Y)mini_batches.append(mini_batch)#如果训练集的大小刚好是mini_batch_size的整数倍,那么这里已经处理完了#如果训练集的大小不是mini_batch_size的整数倍,那么最后肯定会剩下一些,我们要把它处理了if m % mini_batch_size != 0:#获取最后剩余的部分mini_batch_X = shuffled_X[:,mini_batch_size * num_complete_minibatches:]mini_batch_Y = shuffled_Y[:,mini_batch_size * num_complete_minibatches:]mini_batch = (mini_batch_X,mini_batch_Y)mini_batches.append(mini_batch)return mini_batchesnp.random.seed(1)
mini_batch_size = 64
nx = 12288
m = 148
X = np.array([x for x in range(nx * m)]).reshape((m, nx)).T
Y = np.random.randn(1, m) < 0.5mini_batches = random_mini_batches(X, Y, mini_batch_size)
n_batches = len(mini_batches)assert n_batches == math.ceil(m / mini_batch_size), f"Wrong number of mini batches. {n_batches} != {math.ceil(m / mini_batch_size)}"
for k in range(n_batches - 1):assert mini_batches[k][0].shape == (nx, mini_batch_size), f"Wrong shape in {k} mini batch for X"assert mini_batches[k][1].shape == (1, mini_batch_size), f"Wrong shape in {k} mini batch for Y"assert np.sum(np.sum(mini_batches[k][0] - mini_batches[k][0][0], axis=0)) == ((nx * (nx - 1) / 2 ) * mini_batch_size), "Wrong values. It happens if the order of X rows(features) changes"
if ( m % mini_batch_size > 0):assert mini_batches[n_batches - 1][0].shape == (nx, m % mini_batch_size), f"Wrong shape in the last minibatch. {mini_batches[n_batches - 1][0].shape} != {(nx, m % mini_batch_size)}"assert np.allclose(mini_batches[0][0][0][0:3], [294912, 86016, 454656]), "Wrong values. Check the indexes used to form the mini batches"
assert np.allclose(mini_batches[-1][0][-1][0:3], [1425407, 1769471, 897023]), "Wrong values. Check the indexes used to form the mini batches"print("\033[92mAll tests passed!")t_X, t_Y, mini_batch_size = random_mini_batches_test_case()
mini_batches = random_mini_batches(t_X, t_Y, mini_batch_size)print ("shape of the 1st mini_batch_X: " + str(mini_batches[0][0].shape))
print ("shape of the 2nd mini_batch_X: " + str(mini_batches[1][0].shape))
print ("shape of the 3rd mini_batch_X: " + str(mini_batches[2][0].shape))
print ("shape of the 1st mini_batch_Y: " + str(mini_batches[0][1].shape))
print ("shape of the 2nd mini_batch_Y: " + str(mini_batches[1][1].shape))
print ("shape of the 3rd mini_batch_Y: " + str(mini_batches[2][1].shape))
print ("mini batch sanity check: " + str(mini_batches[0][0][0][0:3]))random_mini_batches_test(random_mini_batches)shape of the 1st mini_batch_X: (12288, 64)
shape of the 2nd mini_batch_X: (12288, 64)
shape of the 3rd mini_batch_X: (12288, 20)
shape of the 1st mini_batch_Y: (1, 64)
shape of the 2nd mini_batch_Y: (1, 64)
shape of the 3rd mini_batch_Y: (1, 20)
mini batch sanity check: [ 0.90085595 -0.7612069 0.2344157 ]
All tests passed.
- Shuffling和Partitioning是构建小批量所需的两个步骤
- 二的幂常常被选择为小批量大小,例如16、32、64、128。
4.Momentum
由于小批量梯度下降只看到了一个子集的参数更新,更新的方向有一定的差异,所以小批量梯度下降的路径将“振荡地”走向收敛,使用动量可以减少这些振荡,动量考虑了过去的梯度以平滑更新, 我们将把以前梯度的方向存储在变量v中,从形式上讲,这将是前面的梯度的指数加权平均值。我们也可以把V看作是滚下坡的速度,根据山坡的坡度建立动量。我们来看一下下面的图:
Exercise 3 - initialize_velocity
初始化速度。速度,𝑣, 是一个python字典,需要使用零数组进行初始化。它的关键字与grads字典中的关键字相同,即:

既然我们要影响梯度的方向,而梯度需要使用到dW和db
# GRADED FUNCTION: initialize_velocitydef initialize_velocity(parameters):
"""初始化速度,velocity是一个字典:- keys: "dW1", "db1", ..., "dWL", "dbL" - values:与相应的梯度/参数维度相同的值为零的矩阵。参数:parameters - 一个字典,包含了以下参数:parameters["W" + str(l)] = Wlparameters["b" + str(l)] = bl返回:v - 一个字典变量,包含了以下参数:v["dW" + str(l)] = dWl的速度v["db" + str(l)] = dbl的速度"""L = len(parameters) // 2 #神经网络的层数v = {}for l in range(L):v["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])v["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])return vparameters = initialize_velocity_test_case()v = initialize_velocity(parameters)
print("v[\"dW1\"] =\n" + str(v["dW1"]))
print("v[\"db1\"] =\n" + str(v["db1"]))
print("v[\"dW2\"] =\n" + str(v["dW2"]))
print("v[\"db2\"] =\n" + str(v["db2"]))initialize_velocity_test(initialize_velocity)
Exercise 4 - update_parameters_with_momentum

l:当前神经网络的层数
β:动量,是一个实数
α:学习率
def update_parameters_with_momentun(parameters,grads,v,beta,learning_rate):"""使用动量更新参数参数:parameters - 一个字典类型的变量,包含了以下字段:parameters["W" + str(l)] = Wlparameters["b" + str(l)] = blgrads - 一个包含梯度值的字典变量,具有以下字段:grads["dW" + str(l)] = dWlgrads["db" + str(l)] = dblv - 包含当前速度的字典变量,具有以下字段:v["dW" + str(l)] = ...v["db" + str(l)] = ...beta - 超参数,动量,实数learning_rate - 学习率,实数返回:parameters - 更新后的参数字典v - 包含了更新后的速度变量"""L = len(parameters) // 2 # Momentum update for each parameterfor l in range(1, L + 1):v["dW" + str(l)] = beta * v["dW" + str(l)] + (1 - beta) * grads["dW" + str(l)]v["db" + str(l)] = beta * v["db" + str(l)] + (1 - beta) * grads["db" + str(l)]# update parametersparameters["W" + str(l)] = parameters["W" + str(l)] - learning_rate * v["dW" + str(l)]parameters["b" + str(l)] = parameters["b" + str(l)] - learning_rate * v["db" + str(l)]return parameters, vparameters, grads, v = update_parameters_with_momentum_test_case()parameters, v = update_parameters_with_momentum(parameters, grads, v, beta = 0.9, learning_rate = 0.01)
print("W1 = \n" + str(parameters["W1"]))
print("b1 = \n" + str(parameters["b1"]))
print("W2 = \n" + str(parameters["W2"]))
print("b2 = \n" + str(parameters["b2"]))
print("v[\"dW1\"] = \n" + str(v["dW1"]))
print("v[\"db1\"] = \n" + str(v["db1"]))
print("v[\"dW2\"] = \n" + str(v["dW2"]))
print("v[\"db2\"] = v" + str(v["db2"]))update_parameters_with_momentum_test(update_parameters_with_momentum)
需要注意的是速度v 是用0来初始化的,因此,该算法需要经过几次迭代才能把速度提升上来并开始跨越更大步伐。当beta=0时,该算法相当于是没有使用momentum算法的标准的梯度下降算法。当beta越大的时候,说明平滑的作用越明显。0.8-0.99是对于beta正常的范围,通常0.9是比较合适的值。那如何才能在开始的时候就保持很快的速度向最小误差那里前进呢?我们来看看下面的Adam算法。
5.Adam
Adam算法是训练神经网络中最有效的算法之一,它是RMSProp算法与Momentum算法的结合体。我们来看看它都干了些什么吧~
- 计算以前的梯度的指数加权平均值,并将其存储在变量v(偏差校正前)和
(偏差校正后)中。
- 计算以前梯度的平方的指数加权平均值,并将其存储在变量s(偏差校正前)和
(偏差校正后)中。
- 根据1和2更新参数。
for l = 1...L:

t :当前迭代的次数
l:当前神经网络的层数
beta1 和 beta2:控制两个指数加权平均值的超参数
α :学习率
ε:一个非常小的数,用于避免除零操作,一般为
Exercise 5 - initialize_adam

def initialize_adam(parameters):"""初始化v和s,它们都是字典类型的变量,都包含了以下字段:- keys: "dW1", "db1", ..., "dWL", "dbL" - values:与对应的梯度/参数相同维度的值为零的numpy矩阵参数:parameters - 包含了以下参数的字典变量:parameters["W" + str(l)] = Wlparameters["b" + str(l)] = bl返回:v - 包含梯度的指数加权平均值,字段如下:v["dW" + str(l)] = ...v["db" + str(l)] = ...s - 包含平方梯度的指数加权平均值,字段如下:s["dW" + str(l)] = ...s["db" + str(l)] = ..."""L = len(parameters) // 2 # number of layers in the neural networksv = {}s = {}for l in range(1, L + 1):v["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])v["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])s["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])s["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])return v, sparameters = initialize_adam_test_case()v, s = initialize_adam(parameters)
print("v[\"dW1\"] = \n" + str(v["dW1"]))
print("v[\"db1\"] = \n" + str(v["db1"]))
print("v[\"dW2\"] = \n" + str(v["dW2"]))
print("v[\"db2\"] = \n" + str(v["db2"]))
print("s[\"dW1\"] = \n" + str(s["dW1"]))
print("s[\"db1\"] = \n" + str(s["db1"]))
print("s[\"dW2\"] = \n" + str(s["dW2"]))
print("s[\"db2\"] = \n" + str(s["db2"]))initialize_adam_test(initialize_adam)
Exercise 6 - update_parameters_with_adam

def update_parameters_with_adam(parameters,grads,v,s,t,learning_rate=0.01,beta1=0.9,beta2=0.999,epsilon=1e-8):"""使用Adam更新参数参数:parameters - 包含了以下字段的字典:parameters['W' + str(l)] = Wlparameters['b' + str(l)] = blgrads - 包含了梯度值的字典,有以下key值:grads['dW' + str(l)] = dWlgrads['db' + str(l)] = dblv - Adam的变量,第一个梯度的移动平均值,是一个字典类型的变量s - Adam的变量,平方梯度的移动平均值,是一个字典类型的变量t - 当前迭代的次数learning_rate - 学习率beta1 - 动量,超参数,用于第一阶段,使得曲线的Y值不从0开始(参见天气数据的那个图)beta2 - RMSprop的一个参数,超参数epsilon - 防止除零操作(分母为0)返回:parameters - 更新后的参数v - 第一个梯度的移动平均值,是一个字典类型的变量s - 平方梯度的移动平均值,是一个字典类型的变量"""L = len(parameters) // 2v_corrected = {} #偏差修正后的值s_corrected = {} #偏差修正后的值for l in range(1, L + 1):v["dW" + str(l)] = beta1 * v["dW" + str(l)] + (1 - beta1) * grads["dW" + str(l)]v["db" + str(l)] = beta1 * v["db" + str(l)] + (1 - beta1) * grads["db" + str(l)]v_corrected["dW" + str(l)] = v["dW" + str(l)] / (1 - np.power(beta1, t))v_corrected["db" + str(l)] = v["db" + str(l)] / (1 - np.power(beta1, t))s["dW" + str(l)] = beta2 * s["dW" + str(l)] + (1 - beta2) * np.square(grads["dW" + str(l)])s["db" + str(l)] = beta2 * s["db" + str(l)] + (1 - beta2) * np.square(grads["db" + str(l)])s_corrected["dW" + str(l)] = s["dW" + str(l)] / (1 - np.power(beta2, t))s_corrected["db" + str(l)] = s["db" + str(l)] / (1 - np.power(beta2, t))parameters["W" + str(l)] = parameters["W" + str(l)] - learning_rate * (v_corrected["dW" + str(l)] / (np.sqrt(s_corrected["dW" + str(l)]) + epsilon))parameters["b" + str(l)] = parameters["b" + str(l)] - learning_rate * (v_corrected["db" + str(l)] / (np.sqrt(s_corrected["db" + str(l)]) + epsilon))return parameters, v, s, v_corrected, s_correctedparametersi, grads, vi, si, t, learning_rate, beta1, beta2, epsilon = update_parameters_with_adam_test_case()parameters, v, s, vc, sc = update_parameters_with_adam(parametersi, grads, vi, si, t, learning_rate, beta1, beta2, epsilon)
print(f"W1 = \n{parameters['W1']}")
print(f"W2 = \n{parameters['W2']}")
print(f"b1 = \n{parameters['b1']}")
print(f"b2 = \n{parameters['b2']}")update_parameters_with_adam_test(update_parameters_with_adam)
6.具有不同优化算法的模型
下面,您将使用以下“moons”数据集来测试不同的优化方法。(该数据集被命名为“月亮”,因为这两个类别的数据看起来都有点像新月。)
train_X, train_Y = load_dataset()

def model(X,Y,layers_dims,optimizer,learning_rate=0.0007,mini_batch_size=64,beta=0.9,beta1=0.9,beta2=0.999,epsilon=1e-8,num_epochs=10000,print_cost=True,is_plot=True):"""可以运行在不同优化器模式下的3层神经网络模型。参数:X - 输入数据,维度为(2,输入的数据集里面样本数量)Y - 与X对应的标签layers_dims - 包含层数和节点数量的列表optimizer - 字符串类型的参数,用于选择优化类型,【 "gd" | "momentum" | "adam" 】learning_rate - 学习率mini_batch_size - 每个小批量数据集的大小beta - 用于动量优化的一个超参数beta1 - 用于计算梯度后的指数衰减的估计的超参数beta1 - 用于计算平方梯度后的指数衰减的估计的超参数epsilon - 用于在Adam中避免除零操作的超参数,一般不更改num_epochs - 整个训练集的遍历次数,(视频2.9学习率衰减,1分55秒处,视频中称作“代”),相当于之前的num_iterationprint_cost - 是否打印误差值,每遍历1000次数据集打印一次,但是每100次记录一个误差值,又称每1000代打印一次is_plot - 是否绘制出曲线图返回:parameters - 包含了学习后的参数"""L = len(layers_dims)costs = []t = 0 #每学习完一个minibatch就增加1seed = 10 #随机种子#初始化参数parameters = opt_utils.initialize_parameters(layers_dims)#选择优化器if optimizer == "gd":pass #不使用任何优化器,直接使用梯度下降法elif optimizer == "momentum":v = initialize_velocity(parameters) #使用动量elif optimizer == "adam":v, s = initialize_adam(parameters)#使用Adam优化else:print("optimizer参数错误,程序退出。")exit(1)#开始学习for i in range(num_epochs):#定义随机 minibatches,我们在每次遍历数据集之后增加种子以重新排列数据集,使每次数据的顺序都不同seed = seed + 1minibatches = random_mini_batches(X,Y,mini_batch_size,seed)for minibatch in minibatches:#选择一个minibatch(minibatch_X,minibatch_Y) = minibatch#前向传播A3 , cache = opt_utils.forward_propagation(minibatch_X,parameters)#计算误差cost = opt_utils.compute_cost(A3 , minibatch_Y)#反向传播grads = opt_utils.backward_propagation(minibatch_X,minibatch_Y,cache)#更新参数if optimizer == "gd":parameters = update_parameters_with_gd(parameters,grads,learning_rate)elif optimizer == "momentum":parameters, v = update_parameters_with_momentun(parameters,grads,v,beta,learning_rate)elif optimizer == "adam":t = t + 1 parameters , v , s = update_parameters_with_adam(parameters,grads,v,s,t,learning_rate,beta1,beta2,epsilon)#记录误差值if i % 100 == 0:costs.append(cost)#是否打印误差值if print_cost and i % 1000 == 0:print("第" + str(i) + "次遍历整个数据集,当前误差值:" + str(cost))#是否绘制曲线图if is_plot:plt.plot(costs)plt.ylabel('cost')plt.xlabel('epochs (per 100)')plt.title("Learning rate = " + str(learning_rate))plt.show()return parameters6.1Mini-Batch梯度下降
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")# Predict
predictions = predict(train_X, train_Y, parameters)# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
6.2带有Momentum的Mini-Batch梯度下降
接下来,运行以下代码来查看模型如何处理动量。因为这个例子相对简单,所以使用动量的gains很小,但对于更复杂的问题,你可能会看到更大的gains。
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")# Predict
predictions = predict(train_X, train_Y, parameters)# Plot decision boundary
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)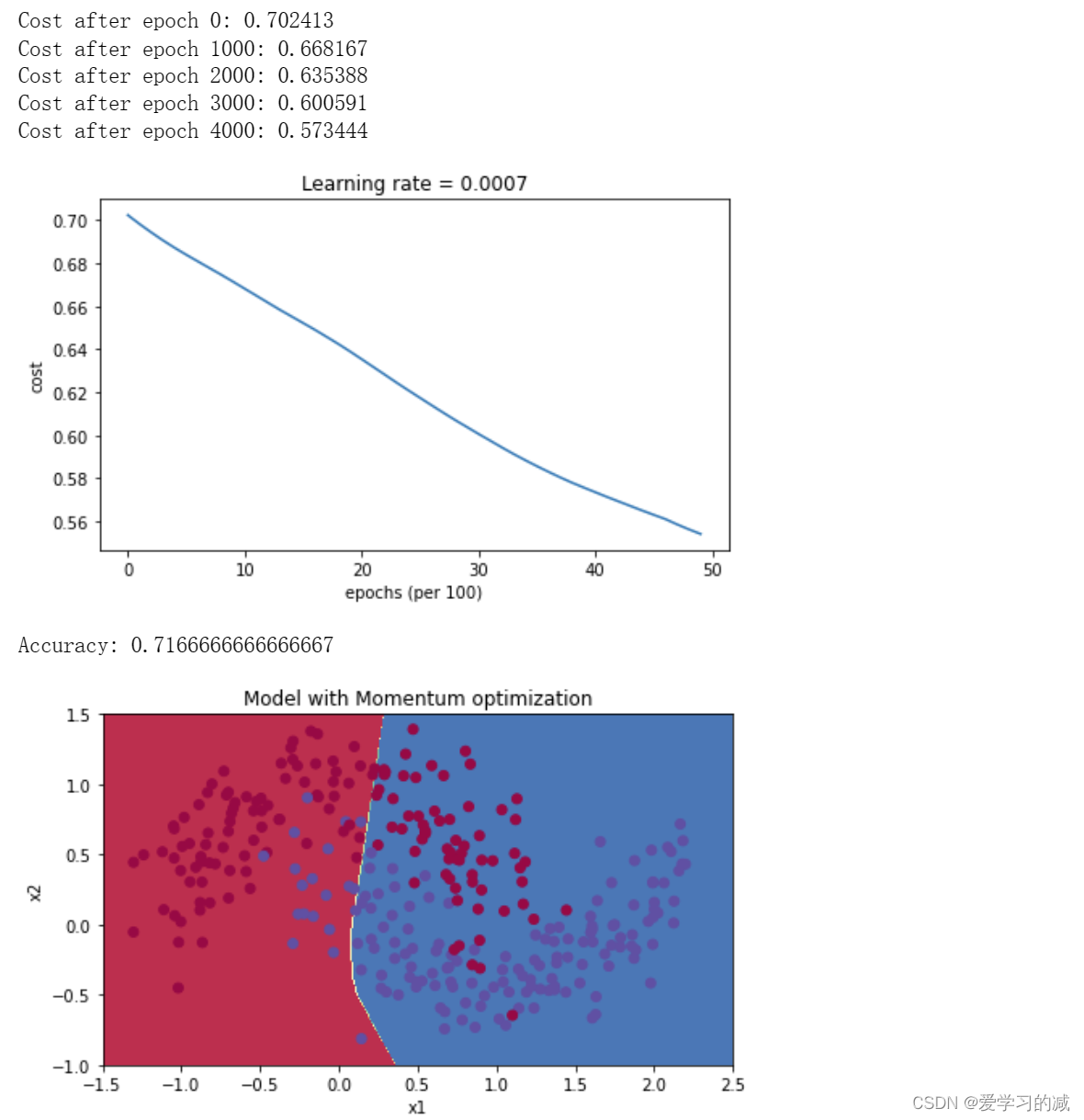
6.3用Adam的Mini-Batch梯度下降
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")# Predict
predictions = predict(train_X, train_Y, parameters)# Plot decision boundary
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
6.4总结

具有动量的梯度下降通常可以有很好的效果,但由于小的学习速率和简单的数据集所以它的影响几乎是轻微的。另一方面,Adam明显优于小批量梯度下降和具有动量的梯度下降,如果在这个简单的模型上运行更多时间的数据集,这三种方法都会产生非常好的结果,然而,我们已经看到Adam收敛得更快。Adam的一些优点包括相对较低的内存要求(虽然比梯度下降和动量下降更高)和通常运作良好,即使对参数进行微调(除了学习率α)
7.学习率衰退与进度安排
最后,学习率是另一个可以帮助你加快学习速度的超参数。
在训练的第一部分,你的模型可以大踏步前进,但随着时间的推移,使用固定的学习率α值可能会导致你的模型陷入一个永远不会完全收敛的大范围振荡中。但是,如果你要随着时间的推移慢慢降低你的学习率α,那么你可以采取更小、更慢的步骤,使你更接近最低水平。这就是学习率衰减背后的思想。
学习率衰减可以通过使用自适应方法或预定义的学习率时间表来实现。
现在,您将以三种不同的优化器模式将计划学习率衰减应用于三层神经网络,并了解每种模式的不同之处,以及不同时期的调度效果。
这个模型与你之前使用的模型基本相同,只是在这个模型中你可以包括学习率衰减。它包括两个新的参数,衰变和衰变率。
def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8, num_epochs = 5000, print_cost = True, decay=None, decay_rate=1):L = len(layers_dims) # number of layers in the neural networkscosts = [] # to keep track of the costt = 0 # initializing the counter required for Adam updateseed = 10 # For grading purposes, so that your "random" minibatches are the same as oursm = X.shape[1] # number of training exampleslr_rates = []learning_rate0 = learning_rate # the original learning rate# Initialize parametersparameters = initialize_parameters(layers_dims)# Initialize the optimizerif optimizer == "gd":pass # no initialization required for gradient descentelif optimizer == "momentum":v = initialize_velocity(parameters)elif optimizer == "adam":v, s = initialize_adam(parameters)# Optimization loopfor i in range(num_epochs):# Define the random minibatches. We increment the seed to reshuffle differently the dataset after each epochseed = seed + 1minibatches = random_mini_batches(X, Y, mini_batch_size, seed)cost_total = 0for minibatch in minibatches:# Select a minibatch(minibatch_X, minibatch_Y) = minibatch# Forward propagationa3, caches = forward_propagation(minibatch_X, parameters)# Compute cost and add to the cost totalcost_total += compute_cost(a3, minibatch_Y)# Backward propagationgrads = backward_propagation(minibatch_X, minibatch_Y, caches)# Update parametersif optimizer == "gd":parameters = update_parameters_with_gd(parameters, grads, learning_rate)elif optimizer == "momentum":parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)elif optimizer == "adam":t = t + 1 # Adam counterparameters, v, s, _, _ = update_parameters_with_adam(parameters, grads, v, s,t, learning_rate, beta1, beta2, epsilon)cost_avg = cost_total / mif decay:learning_rate = decay(learning_rate0, i, decay_rate)# Print the cost every 1000 epochif print_cost and i % 1000 == 0:print ("Cost after epoch %i: %f" %(i, cost_avg))if decay:print("learning rate after epoch %i: %f"%(i, learning_rate))if print_cost and i % 100 == 0:costs.append(cost_avg)# plot the costplt.plot(costs)plt.ylabel('cost')plt.xlabel('epochs (per 100)')plt.title("Learning rate = " + str(learning_rate))plt.show()return parameters7.1每次迭代时衰减

Exercise 7 - update_lr
使用指数权重衰减计算新的学习率。
def update_lr(learning_rate0, epoch_num, decay_rate):
"""
使用指数权重衰减计算更新的学习率。参数:
learning_rate0——原始学习率。标量
epoch_num——epoch数。整数
decay_rate——衰变率。标量返回:
learning_rate——更新的学习率。标量
"""learning_rate = learning_rate0 / (1 + decay_rate * epoch_num)return learning_ratelearning_rate = 0.5
print("Original learning rate: ", learning_rate)
epoch_num = 2
decay_rate = 1
learning_rate_2 = update_lr(learning_rate, epoch_num, decay_rate)print("Updated learning rate: ", learning_rate_2)update_lr_test(update_lr)Original learning rate: 0.5
Updated learning rate: 0.16666666666666666
All tests passed
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd", learning_rate = 0.1, num_epochs=5000, decay=update_lr)# Predict
predictions = predict(train_X, train_Y, parameters)# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
请注意,如果您将衰减设置为在每次迭代时发生,则学习率会过快变为零——即使您从更高的学习率开始。

当你训练几个epoch时,这不会引起很多麻烦,但当epoch的数量很大时,优化算法会停止更新。解决这个问题的一个常见方法是每隔几步就降低学习率。这被称为固定间隔调度。
7.2固定间隔调度
通过将指数学习率衰减安排在固定的时间间隔(例如1000),可以帮助防止学习率过快地变为零。您可以对时间间隔进行编号,也可以将epoch除以时间间隔,时间间隔是具有恒定学习率的窗口大小。

Exercise 8 - schedule_lr_decay
使用具有固定间隔调度的指数权重衰减来计算新的学习率。

def schedule_lr_decay(learning_rate0, epoch_num, decay_rate, time_interval=1000):learning_rate = learning_rate0 / (1 + decay_rate * (epoch_num // time_interval))return learning_ratelearning_rate = 0.5
print("Original learning rate: ", learning_rate)epoch_num_1 = 10
epoch_num_2 = 100
decay_rate = 0.3
time_interval = 100
learning_rate_1 = schedule_lr_decay(learning_rate, epoch_num_1, decay_rate, time_interval)
learning_rate_2 = schedule_lr_decay(learning_rate, epoch_num_2, decay_rate, time_interval)
print("Updated learning rate after {} epochs: ".format(epoch_num_1), learning_rate_1)
print("Updated learning rate after {} epochs: ".format(epoch_num_2), learning_rate_2)schedule_lr_decay_test(schedule_lr_decay)Original learning rate: 0.5
Updated learning rate after 10 epochs: 0.5
Updated learning rate after 100 epochs: 0.3846153846153846
All tests passed
7.3对每种优化方法使用学习率衰减
7.3.1Gradient Descent with Learning Rate Decay
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd", learning_rate = 0.1, num_epochs=5000, decay=schedule_lr_decay)# Predict
predictions = predict(train_X, train_Y, parameters)# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

7.3.2 Gradient Descent with Momentum and Learning Rate Decay
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "momentum", learning_rate = 0.1, num_epochs=5000, decay=schedule_lr_decay)# Predict
predictions = predict(train_X, train_Y, parameters)# Plot decision boundary
plt.title("Model with Gradient Descent with momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

7.3.3Adam with Learning Rate Decay
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam", learning_rate = 0.01, num_epochs=5000, decay=schedule_lr_decay)# Predict
predictions = predict(train_X, train_Y, parameters)# Plot decision boundary
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)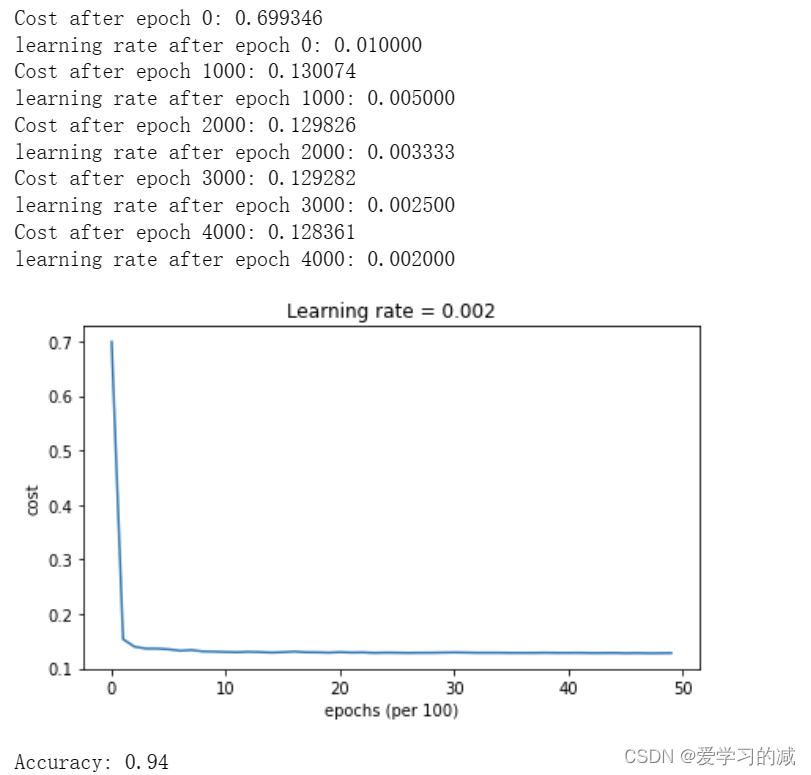

7.4用不同的方法实现相似的性能
使用Mini batch GD或Mini batch-GD With Momentum,精度明显低于Adam,但当在顶部添加学习率衰减时,两者都可以以与Adam相似的速度和精度得分实现性能。
在Adam的情况下,请注意,学习曲线达到了类似的精度,但速度更快。

相关文章:

吴恩达深度学习l2week2编程作业—Optimization Methods(最新中文跑通版)
到目前为止,您一直使用渐变下降来更新参数并将成本降至最低。在本笔记本中,您将获得一些更先进的优化方法的技能,这些方法可以加快学习速度,甚至可能使您获得更好的成本函数最终值。拥有一个好的优化算法可能是等待几天与只需几个…...

每日一题——LeetCode1089.复写0
方法一 splice: 通过数组的slice方法,碰到 0就在后面加一个0,最后截取原数组的长度,舍弃后面部分。 但这样做是违反了题目的要求,不要在超过该数组长度的位置写入元素。 var duplicateZeros function(arr) {var le…...
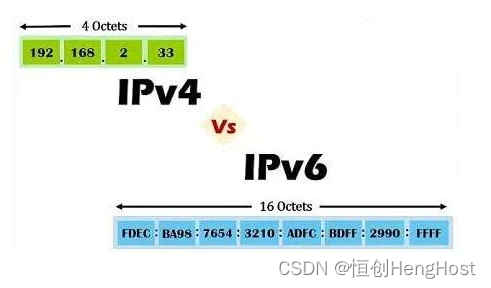
IPv6和IPv4在技术层面的区别
随着互联网的不断发展,IPv4地址资源已经逐渐枯竭,而IPv6地址的使用逐渐成为趋势。IPv6和IPv4作为互联网协议的两个版本,在技术层面存在许多区别。本文将从地址空间、地址表示方法、路由协议、安全性、移动性以及网络性能等方面对IPv6和IPv4进…...

如何充值GPT会员账号?
详情点击链接:如何充值GPT会员账号? 一OpenAI 1.最新大模型GPT-4 Turbo 2.最新发布的高级数据分析,AI画图,图像识别,文档API 3.GPT Store 4.从0到1创建自己的GPT应用 5. 模型Gemini以及大模型Claude2二定制自己的…...
设计模式:单例模式
文章目录 1、概念2、实现方式1、懒汉式2、饿汉式3、双检锁/双重校验锁4、登记式/静态内部类5、枚举6、容器实现单例 1、概念 单例模式(Singleton Pattern)是 Java 中最简单的设计模式之一。这种类型的设计模式属于创建型模式,它提供了一种创…...

启动 Mac 时显示闪烁的问号
启动 Mac 时显示闪烁的问号 如果启动时在 Mac 屏幕上看到闪烁的问号,这意味着你的 Mac 无法找到自身的系统软件。 如果 Mac 启动时出现闪烁的问号且无法继续启动,请尝试以下步骤。 1.通过按住其电源按钮几秒钟来关闭 Mac。 2.按一下电源按钮…...
十种编程语言的对比分析
在当今的软件开发领域,编程语言扮演着至关重要的角色。不同的编程语言各有其特点和适用场景,选择合适的编程语言能够提高开发效率和软件质量。本文将对十种常见的编程语言进行对比分析,帮助读者了解它们的优缺点和适用场景。 一、Python Pyt…...

React16源码: React.Children源码实现
React.Children 1 ) 概述 这个API用的也比较的少,因为大部分情况下,我们不会单独去操作children我们在一个组件内部拿到 props 的时候,我们有props.children这么一个属性大部分情况下,直接把 props.children 把它渲染到我们的jsx…...

深度学习|4.1 深L层神经网络 4.2 深层网络的正向传播
4.1 深L层神经网络 对于某些问题来说,深层神经网络相对于浅层神经网络解决该问题的效果会较好。所以问题就变成了神经网络层数的设置。 其中 n [ i ] n^{[i]} n[i]表示第i层神经节点的个数, w [ l ] w^{[l]} w[l]代表计算第l层所采用的权重系数ÿ…...
印象笔记03 衍生软件使用
印象笔记03 衍生软件使用 Verse 以下内容来源于官方介绍 VERSE是一款面向未来的智能化生产力工具,由印象笔记团队诚意推出。 你可以用VERSE: 管理数字内容,让信息有序高效运转;搭建知识体系,构建你的强大知识库&am…...
: 根据通过 method 参数定义的方法,删除或标记地理空间中异常值的记录。)
R语言【CoordinateCleaner】——cc_gbif(): 根据通过 method 参数定义的方法,删除或标记地理空间中异常值的记录。
cc_gbif()是R语言包coordinatecleaner中的一个函数,用于清理GBIF(全球生物多样性信息设施)数据集的地理坐标。该函数可以识别潜在的坐标错误,并对其进行修正或删除。 以下是cc_gbifl()函数的一般用法和主要参数: cc_…...
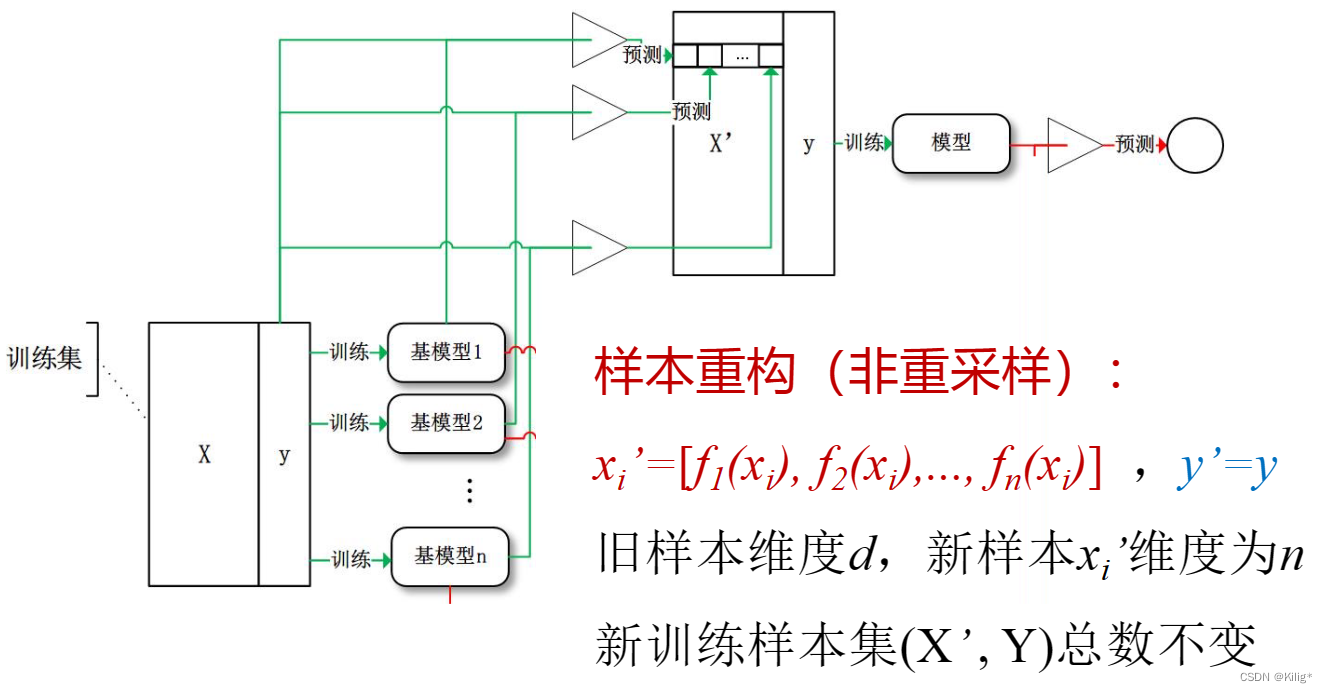
模式识别与机器学习-集成学习
集成学习 集成学习思想过拟合与欠拟合判断方法 K折交叉验证BootstrapBagging随机森林的特点和工作原理: BoostingAdaBoost工作原理:AdaBoost的特点和优点:AdaBoost的缺点: Gradient Boosting工作原理:Gradient Boostin…...
vue简单实现滚动条
背景:产品提了一个需求在一个详情页,一个form表单元素太多了,需要滚动到最下面才能点击提交按钮,很不方便。他的方案是,加一个滚动条,这样可以直接拉到最下面。 优化:1、支持滚动条,…...

计算机网络第一课
先了解层级: 传输的信息称为协议数据单元(PDU),PDU在每个层次的称呼都不同,见下图:...

初识大数据,一文掌握大数据必备知识文集(12)
🏆作者简介,普修罗双战士,一直追求不断学习和成长,在技术的道路上持续探索和实践。 🏆多年互联网行业从业经验,历任核心研发工程师,项目技术负责人。 🎉欢迎 👍点赞✍评论…...

安全防御之授权和访问控制技术
授权和访问控制技术是安全防御中的重要组成部分,主要用于管理和限制对系统资源(如数据、应用程序等)的访问。授权控制用户可访问和操作的系统资源,而访问控制技术则负责在授权的基础上,确保只有经过授权的用户才能访问…...

Iceberg从入门到精通系列之二十:Iceberg支持的字段类型
Iceberg从入门到精通系列之二十:Iceberg支持的字段类型 Iceberg 表支持以下类型: 字段类型描述注释booleanTrue or falseint32 位有符号整数可以提升到longlong64 位有符号整数float32 位 IEEE 754 浮点可以提升到doubledouble64 位 IEEE 754 浮点decim…...
Unity坦克大战开发全流程——结束场景——通关界面
结束场景——通关界面 就照着这样来拼 写代码 hideme不要忘了 修改上一节课中的代码...

K8S三种发布方式和声明式资源管理
蓝绿发布 把应用服务集群标记位两个组,蓝组和绿组,先升级蓝组,先要把蓝组从负载均衡当中移除,绿组继续提供服务,蓝组升级完毕,再把绿组从负载均衡当中移除,绿组升级,然后都加入回负载…...
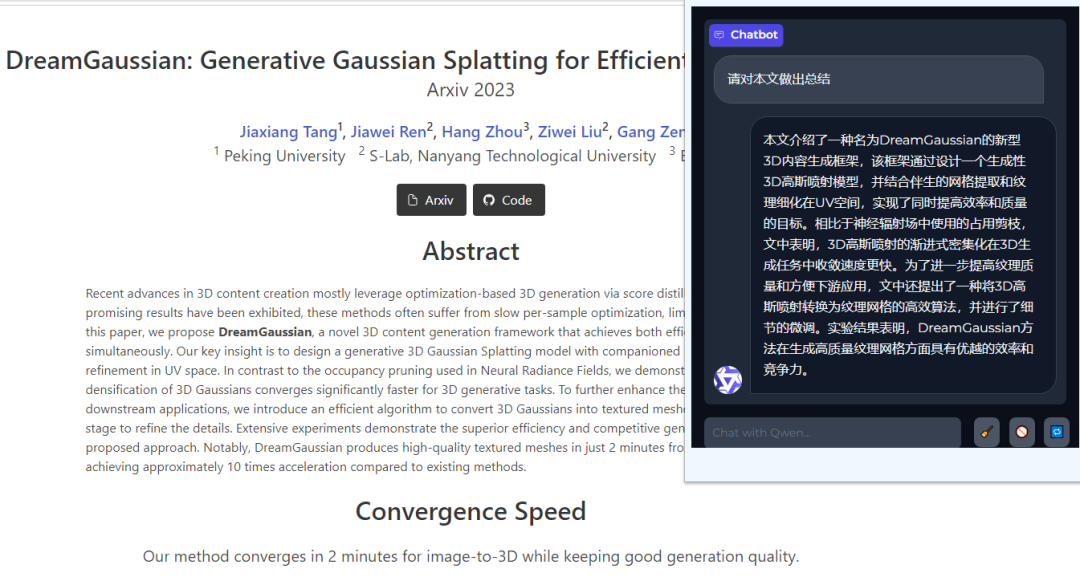
从千问Agent看AI Agent——我们很强,但还有很长的路要走
前言 最近双十一做活动买了台新电脑,显卡好起来了自然也开始大模型的学习工作了,这篇文章可能是该系列的第一弹,本地私有化部署千问agent,后面还会尝试一些其他的大模型结合本地知识库或者做行业垂直模型训练的,一步…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
