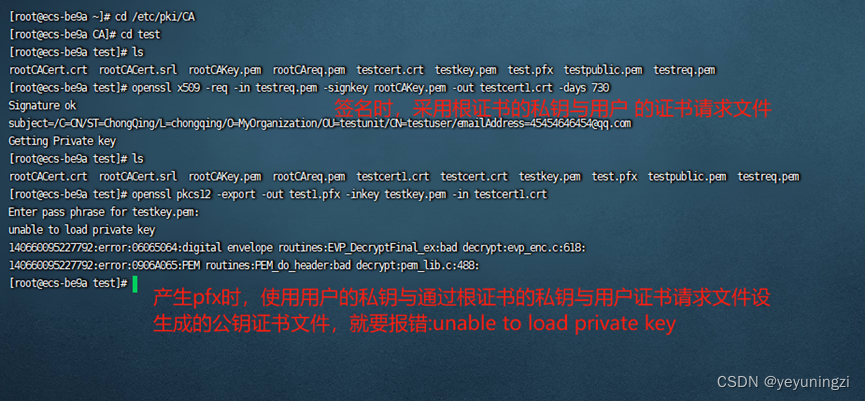
使用openssl 生成pfx格式证书时报错：unable to load certificates
问题现象包如下：
之前在centos上使用openssl部署证书服务器以及颁发证书的时候遇到的问题，在进行个人证书生成之后需要形成pfx格式证书，结果过程中报错了。网上类似资料比较少，做个记录。
生成pfx格式证书的命令：
openssl pkcs12 -export -in 公钥证书文件路径 -inkey 私钥文件路径 -out 要产生的pfx文件路径
-in 后传的是公钥证书文件，而不是公钥文件，公钥证书文件是需要通过私钥与证书请求文件产生的。
正确的是：
openssl pkcs12 -export -inkey testuser2key.pem -in testuser2.crt -out testuser2.pfx
-in 使用的是签名通过证书请求文件已签发的公钥证书文件
-inkey 使用的是私钥文件
-out 指定生成的pfx格式文件 不指定路径为当前目录下
导出pfx格式证书文件时，还提示输入的密码就使用此证书文件需要的密码，要牢记。
centos7 上通过openssl 部署证书服务器以及颁发证书过程，可参考：centos7 使用openssl 配置证书服务器并颁发证书（史上最详细版本）-CSDN博客
相关文章：
使用openssl 生成pfx格式证书时报错：unable to load certificates
问题现象包如下： 之前在centos上使用openssl部署证书服务器以及颁发证书的时候遇到的问题，在进行个人证书生成之后需要形成pfx格式证书，结果过程中报错了。网上类似资料比较少，做个记录。 生成pfx格式证书的命令： o…...
微信小程序 分享按钮 监听用户分享成功
代码 <view><button class"btnLq ed flex justify-center" open-type"share" click"getAward">点击分享</button> </view>export default {data(){return{shareMd:false,//分享埋点}},onShow(){//if(this.shareMd){uni.…...
数据结构-怀化学院期末题
题目： 利用希尔排序算法实现线性表的排序。希尔排序是根据给定的增量序列将线性表分隔成某个“增量”的记录组成一个子序例，在子序列中采用直接插入排序完成。 输入 第一行为元素个数n(1<n<1000)，第二行为n个元素值(整数)，即…...
跟cherno手搓游戏引擎【1】：配置与入口点
环境配置： 编译环境：VS2019 创建两个项目： 设置Sandbox为启动项： 设置sandbox的配置属性-常规-输出目录\中间目录为如下： 预处理定义：为了配置一些只有windows才能用的函数。 设置YOTOEngin（我…...
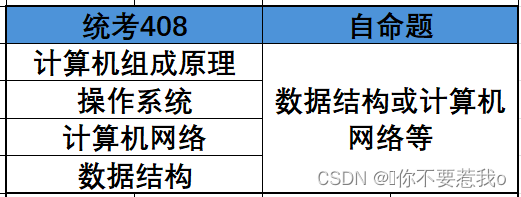
25计算机专业考研经验贴之准备篇
Hello各位小伙伴，大家新年好！ 马上就要进入寒假假期了，25考研也该提上日程了。今天先跟大家分享一下大家在假期可以先做起来的准备工作。 【选择学校】 择校是个非常重要的内容，因为不同学校的考试内容是不一样的，有些…...
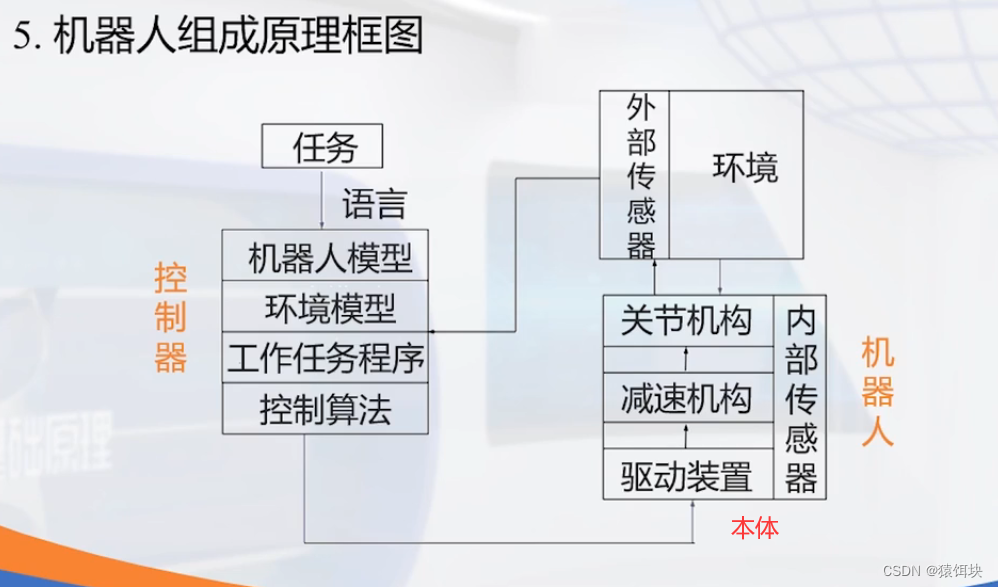
机器人相关知识
机器人学（Robotics) 一些基础概念 位姿 位姿位置姿态 位姿的表示 刚体 刚性物体是一组粒子的集合，其中任意两个粒子之间的距离保持固定，不受物体运动或施加在物体上的力的影响。 “完全不可变形”的物体就是刚体。 刚体位置 刚性连杆 …...
八股文打卡day22——操作系统（5）
面试题：什么是死锁？如何避免死锁？ 我的回答： 死锁是两个或者多个进程都占有各自的资源，然后都互相请求资源，导致互相都陷入了阻塞状态。 如何避免死锁呢？ 首先，造成死锁有四个必要…...
SQL Server 权限管理
CSDN 成就一亿技术人！ 2024年 第一篇 难度指数：* * CSDN 成就一亿技术人！ 目录 1. 权限管理 什么是权限管理？ SQL server的安全机制 服务器级角色 数据库级角色 对象级角色 2. 创建用户 赋予权限 最重要的一步骤 1. 权限…...
ReentrantLock底层原理学习一
J.U.C 简介 Java.util.concurrent 是在并发编程中比较常用的工具类，里面包含很多用来在并发场景中使用的组件。比如线程池、阻塞队列、计时器、同步器、并发集合等等。并发包的作者是大名鼎鼎的 Doug Lea。我们在接下来的课程中，回去剖析一些经典的比较…...
数字孪生在增强现实（AR）中的应用
数字孪生在增强现实（Augmented Reality，AR）中的应用可以提供更丰富、交互性更强的现实世界增强体验。以下是数字孪生在AR中的一些应用，希望对大家有所帮助。北京木奇移动技术有限公司，专业的软件外包开发公司ÿ…...
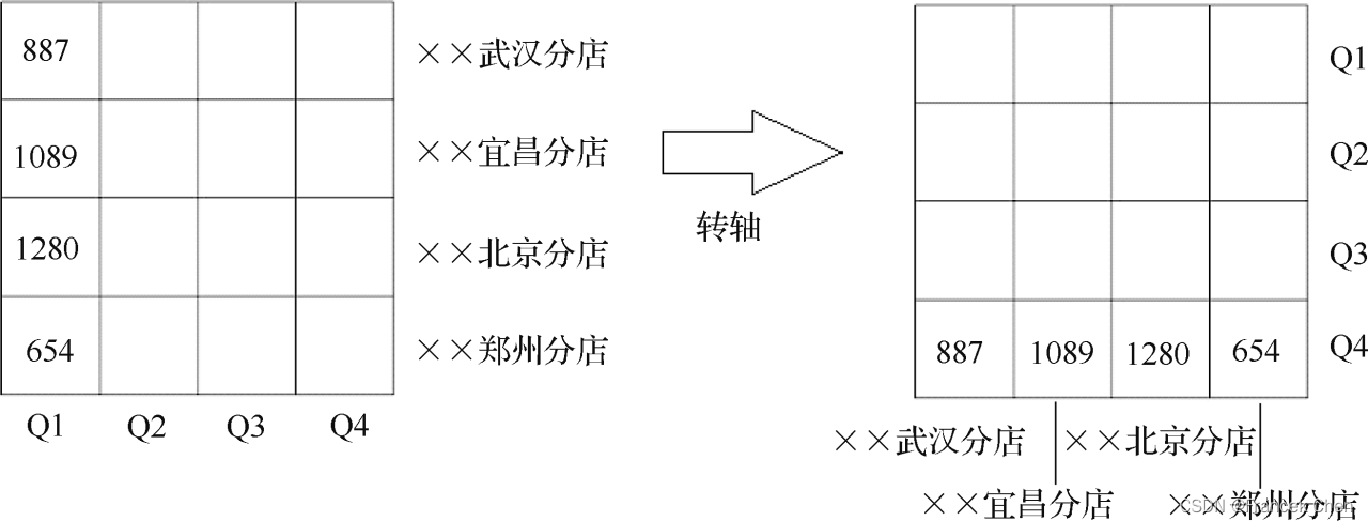
【数据仓库与联机分析处理】多维数据模型
目录 一、数据立方体 二、数据模型 （一）星形模型 （二）雪花模式 （三）事实星座模式 三、多维数据模型中的OLAP操作 （一）下钻 （二）上卷 （三…...
【网络面试（3）】浏览器委托协议栈完成消息的收发
前面的博客中，提到过很多次，浏览器作为应用程序，本身是不具备向网络中发送网络请求的能力，要委托操作系统的内核协议栈来完成。协议栈再调用网卡驱动，通过网卡将请求消息发送出去，本篇博客就来探讨一下这个…...
Kotlin： Jetpack — ViewModel简单应用
ViewModel 概览 Android Jetpack 的一部分。 ViewModel 类是一种业务逻辑或屏幕级状态容器。它用于将状态公开给界面，以及封装相关的业务逻辑。 它的主要优点是，它可以缓存状态，并可在配置更改后持久保留相应状态。这意味着在 activity 之…...
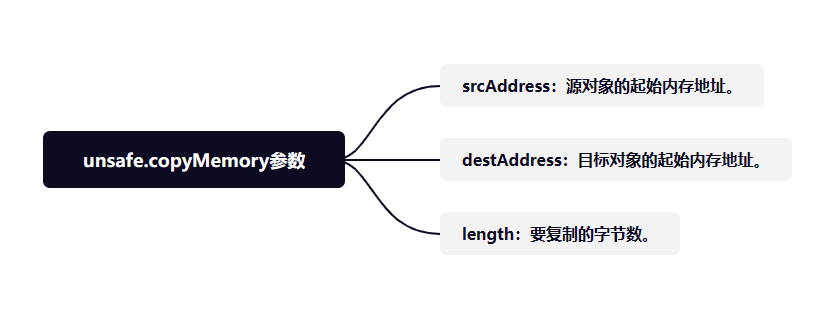
【Java技术专题】「攻破技术盲区」攻破Java技术盲点之unsafe类的使用指南（打破Java的安全管控— sun.misc.unsafe）
Java后门机制 — sun.misc.unsafe 打破Java的安全管控关于Unsafe的编程建议实例化Unsafe后门对象使用sun.misc.Unsafe创建实例单例模式处理实现浅克隆（直接获取内存的方式）直接使用copyMemory原理分析 密码安全使用Unsafe类—示例代码 运行时动态创建类超…...
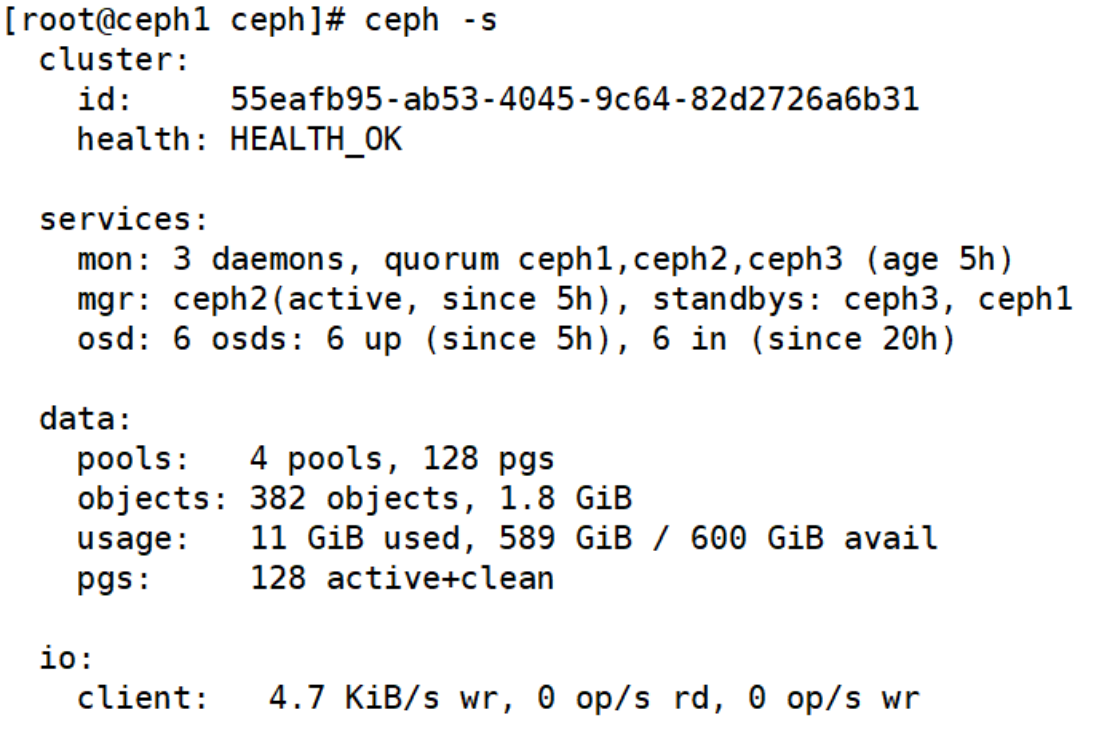
私有云平台搭建openstack和ceph结合搭建手册
OpenStack与云计算 什么是云？ 如何正确理解云，可以从以下几个方面。 云的构成。 用户：对用户而言是透明无感知的，不用关心底层构成，只需要知道利用云完成自己任务即可。 云提供商：对云资产管理和运维。 云…...
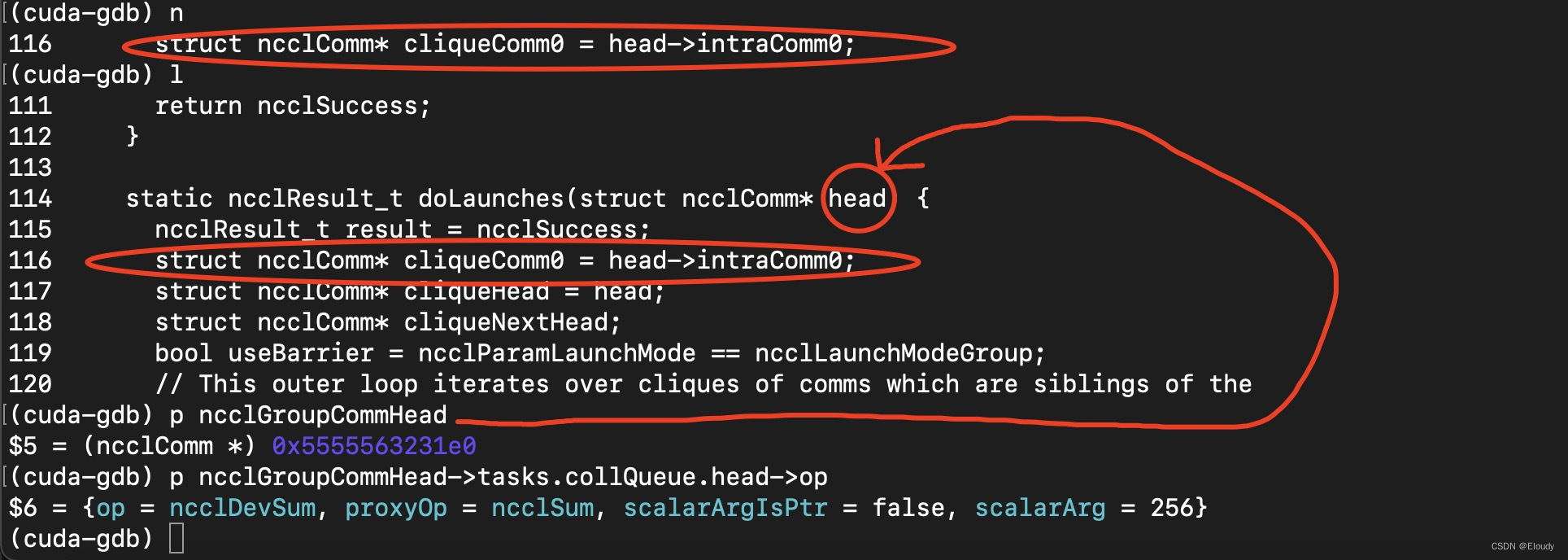
debug mccl 02 —— 环境搭建及初步调试
1, 搭建nccl 调试环境 下载 nccl 源代码 git clone --recursive https://github.com/NVIDIA/nccl.git 只debug host代码，故将设备代码的编译标志改成 -O3 (base) hipperhipper-G21:~/let_debug_nccl/nccl$ git diff diff --git a/makefiles/common.mk b/makefiles/…...
ros python 接收GPS RTK 串口消息再转发 ros 主题消息
代码是一个ROS（Robot Operating System）节点，用于从GPS设备读取RTK（实时动态）数据并通过ROS主题发布。 步骤： 导入必要的模块: rospy 是ROS的Python库，用于ROS的节点、发布者和订阅者。serial 用于串行通信。NavSatFix 和 NavSatStatus 是从GPS接收的NMEA 0183标准消息…...
2024年网络安全竞赛-页面信息发现任务解析
页面信息发现任务说明： 服务器场景：win20230305（关闭链接）在渗透机中对服务器信息收集，将获取到的服务器网站端口作为Flag值提交；访问服务器网站页面，找到主页面中的Flag值信息，将Flag值提交；访问服务器网站页面，找到主页面中的脚本信息，并将Flag值提交；访问服务器…...
ARM DMA使用整理
Direct Memory Access， 直接存储访问。同SPI,IIC,USART等一样，属于MCU的一个外设，用于在不需要MCU介入的情况下进行数据传输。可以将数据从外设传输到flash，也可以将数据从flash传输到外设，或者flash内部数据移动。 它…...
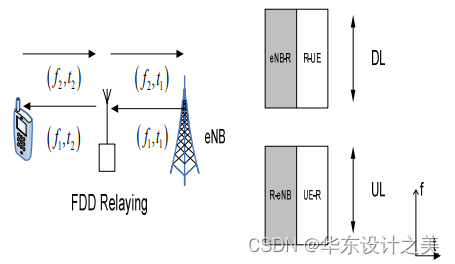
移动通信原理与关键技术学习（第四代蜂窝移动通信系统）
前言：LTE 标准于2008 年底完成了第一个版本3GPP Release 8的制定工作。另一方面，ITU 于2007 年召开了世界无线电会议WRC07，开始了B3G 频谱的分配，并于2008 年完成了IMT-2000（即3G）系统的演进——IMT-Advanc…...
挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手：借助大模型技术，开发能根据用户输入的主题、风格等要求，生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用，帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...
C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为：煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例，提供抽象制作饮品基类，提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
MMaDA: Multimodal Large Diffusion Language Models
CODE ： https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA，它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...
令牌桶 滑动窗口-＞限流 分布式信号量-＞限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结： 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析： 实际业务去理解体会统一注…...
Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明：这是一个机器学习实战项目（附带数据代码文档），如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下，风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体（对象或容器）QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质（定义颜色、反光等）QFirstPersonC…...
从“安全密码”到测试体系：Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码"：Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天，软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力，从金融交易到交通管控，这些关乎国计民生的关键领域…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板（STM32F103RBT6）通过I2C驱动ICM20948九轴传感器，实现姿态解算，并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化，适合嵌入式及物联网开发者。在基础驱动上新增…...
聚六亚甲基单胍盐酸盐市场深度解析：现状、挑战与机遇
根据 QYResearch 发布的市场报告显示，全球市场规模预计在 2031 年达到 9848 万美元，2025 - 2031 年期间年复合增长率（CAGR）为 3.7%。在竞争格局上，市场集中度较高，2024 年全球前十强厂商占据约 74.0% 的市场…...
负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4，后7...