算法导论复习——CHP16 贪心算法
定义
每一步都做出当前看来最优的操作。
问题引入——活动选择问题
问题描述

活动选择问题就是对给定的包含n个活动的集合S,在已知每个活动开始时间和结束时间的条件下,从中选出最多可兼容活动的子集合,称为最大兼容活动集合。 不失一般性,设活动已经按照结束时间单调递增排序。
分析
这个问题具有最优子结构,可以用动态规划,但用贪心复杂度更低。
实际上,任何一个可以用贪心解决的问题都可以用动态规划解决。
这里的贪心策略为:每次都选择能选择的活动中结束时间最早的活动。
证明贪心正确性:
感性上,这样做可以为后面留出最多的时间。
严格证明,只需证明如下定理:
考虑任意非空子问题
,令
是
中结束时间最早的活动,则
必在
的某个最大兼容活动子集中。
证明:
设
为
的一个最大兼容活动子集,
中最早结束的活动为
。
若
,则成立。
若
,则设
,由于
中活动兼容,有
结束时间比
中最早的还早,故
也是
的一个兼容活动子集,又
,故
也是
的一个最大兼容活动子集,故
在
的某个最大兼容活动子集中,也成立。
证毕。
实现
自顶向下

自底向上
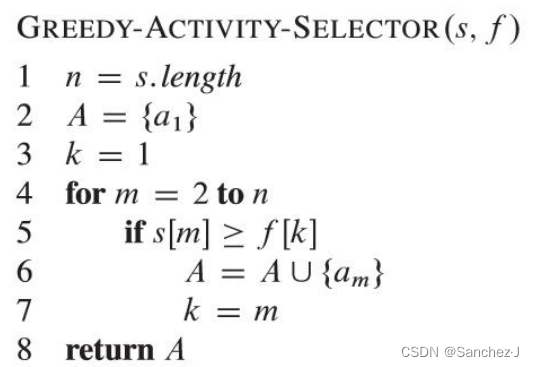
总结——贪心算法的一般步骤
1)确定问题的最优子结构;
2)将最优化问题转化为这样的形式:每次对其作出选择后,只剩下一个子问题需要求解;
3)证明作出贪心选择后,剩余的子问题满足:其最优子解与前面的贪心选择组合即可得到原问题的最优解(具有最优子结构)。
总结——证明贪心算法正确性
贪心选择性质和最优子结构性是两个关键要素。
贪心选择性质:可以通过做出局部最优(贪心)选择来构造全局最优解的性质。
贪心选择性质使得我们进行选择时,只需做出当前看起来最优的选择,而不用考虑子问题的解。
例子——Huffman编码
Huffman算法
从 |C| 个叶子结点开始,每次选择频率最低的两个结点合并,将得到的新结点加入集合继续合并,这样执行 |C|-1次 “合并” 后即可构造出一棵编码树——Huffman树。

(采用以freq为关键字的最小优先队列Q,提取两个最低频率的对象将之合并。)
时间复杂度分析
假设Q使用最小二叉堆实现,则:
首先,Q的初始化时间复杂度O(n)。
其次,循环的总代价是O(nlgn):for循环共执行了n-1次,每次从堆中找出当前频率最小的两个结点及把合并得到的新结点插入到堆中均花费O(lgn),所以循环的总代价是O(nlgn)。
总时间复杂度O(nlgn)。
正确性证明
首先,可以发现,一个最优字符编码方案总对应一棵满 (full) 二叉树, 即每个非叶子结点都有两个孩子结点。
引理1
令C为一个字母表,其中每个字符 c∈C 都有一个频率 c.freq。 令 x 和 y 是C中频率最低的两个字符。那么存在C的一个最优前缀码,x和y的码字长度相同,且只有最后一个二进制位不同。
证:
令T是一个最优前缀码所对应的编码树,a和b是T中深度最大的兄弟叶结点。 不失一般性,假设 a.freq ≤ b.freq 且 x.freq ≤ y.freq。
由于x和y是叶结点中频率最低的两个结点,所以应有 x.freq ≤ a.freq 且y.freq ≤ b.freq。
若 x.freq = b.freq,则有a.freq = b.freq = x.freq = y.freq,此时引理成立。
若 x.freq ≠ b.freq,即 x≠ b。则在T中交换 x 和 a,生成一棵 新树T’ ;然后再在T’中交换 b和y,生成另一棵新树T” ,那么在T”中x和y是深度最深的两个兄弟结点。
计算代价差:
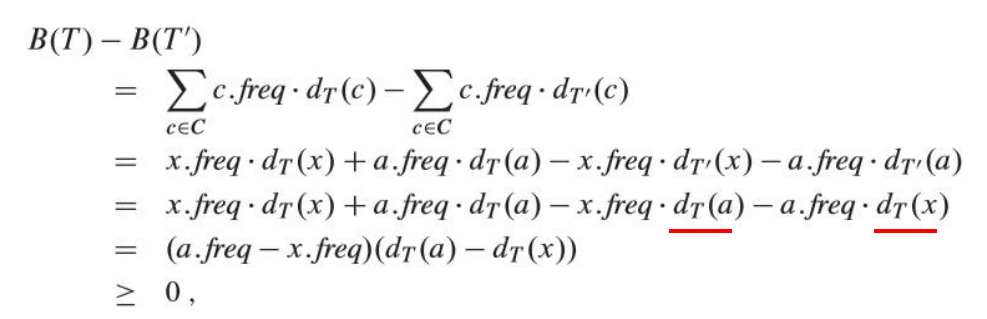
同理有
因此,又B(T)为最优编码,故
即得证:T” 也是最优解,且 x 和 y 是其中深度最大的两个兄弟结点,x和y的码字长度相同,且只有最后一个二进制位不同。
引理2
令C为一个给定的字母表,其中每个字符c∈C都有一 个频率c.freq。x和y是C中频率最低的两个字符。
令C'为C去掉字符x和y,并加入一个新字符z后得到的字母表, 即C' = C - {x, y}∪{z},z.freq= x.freq + y.freq。 令T'为字母表C'的任意一个最优前缀码对应的编码树。
则有:可以将T'中叶子结点 z 替换为一个以x和y为孩子的内部结点,得到树T,而T表示字母表C的一个最优前缀码。
由引理1、2可得Huffman算法的正确性。
相关文章:
算法导论复习——CHP16 贪心算法
定义 每一步都做出当前看来最优的操作。 问题引入——活动选择问题 问题描述 活动选择问题就是对给定的包含n个活动的集合S,在已知每个活动开始时间和结束时间的条件下,从中选出最多可兼容活动的子集合,称为最大兼容活动集合。 不失一般性&a…...
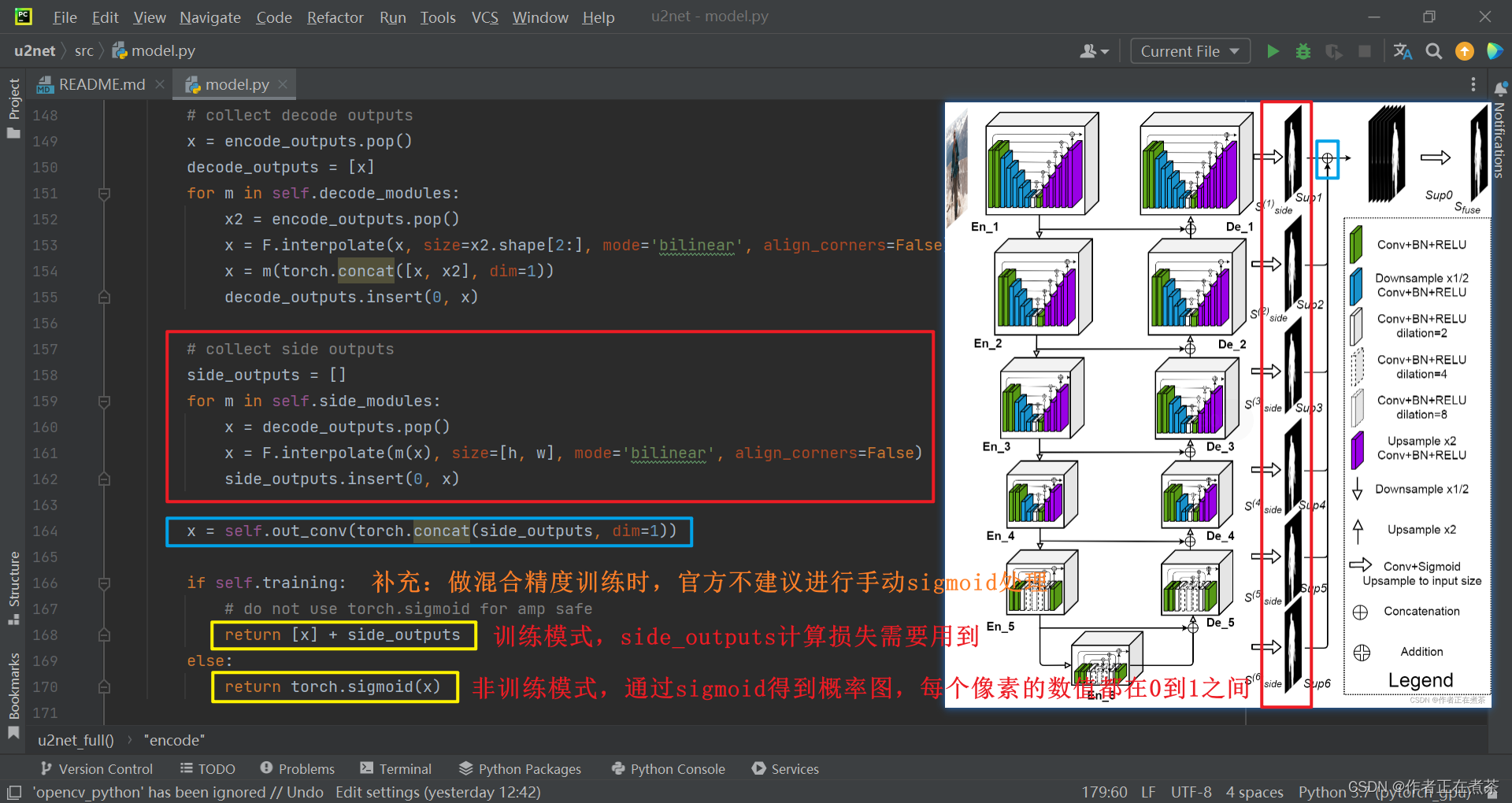
【霹雳吧啦】手把手带你入门语义分割の番外12:U2-Net 源码讲解(PyTorch)—— 网络的搭建
目录 前言 Preparation 一、U2-Net 网络结构图 二、U2-Net 网络源代码 1、model.py (1)ConvBNReLU 类 (2)DownConvBNReLU 类 (3)UpConvBNReLU 类 (4)RSU 类 & RSU4F 类…...

phpstudy面板Table ‘mysql.proc‘ doesn‘t exist解决办法
原因分析:误删了mysql数据库 解决办法如下: 1、停止服务 2、先把mysql文件夹下的data文件夹备份,因为data文件里存有数据库文件。然后再删除data文件。 3、cmd管理员命令进入到mysql中的bin目录下 ,执行mysqld --initialize-…...

网安入门09-Sql注入(绕过方法梳理)
ByPass SQL注入ByPass是指攻击者通过各种手段绕过应用程序中已经实施的SQL注入防御措施,例如输入恶意数据、修改请求头等方式,绕过过滤、转义、限制等操作,从而成功地执行恶意SQL语句。攻击者使用SQL注入ByPass技术可以让应用程序的防御措施…...
本地计算机 上的 My5OL808 服务启动后停止,某些服务在未由其他服务或程序使用时将自动停止
客户反馈说mysql启动不了,报错信息: 本地计算机 上的 My5OL808 服务启动后停止,某些服务在未由其他服务或程序使用时将自动停止。 查了不少资料,最后分析问题是这样的,手动或者重复安装mysql时,创建了多个…...
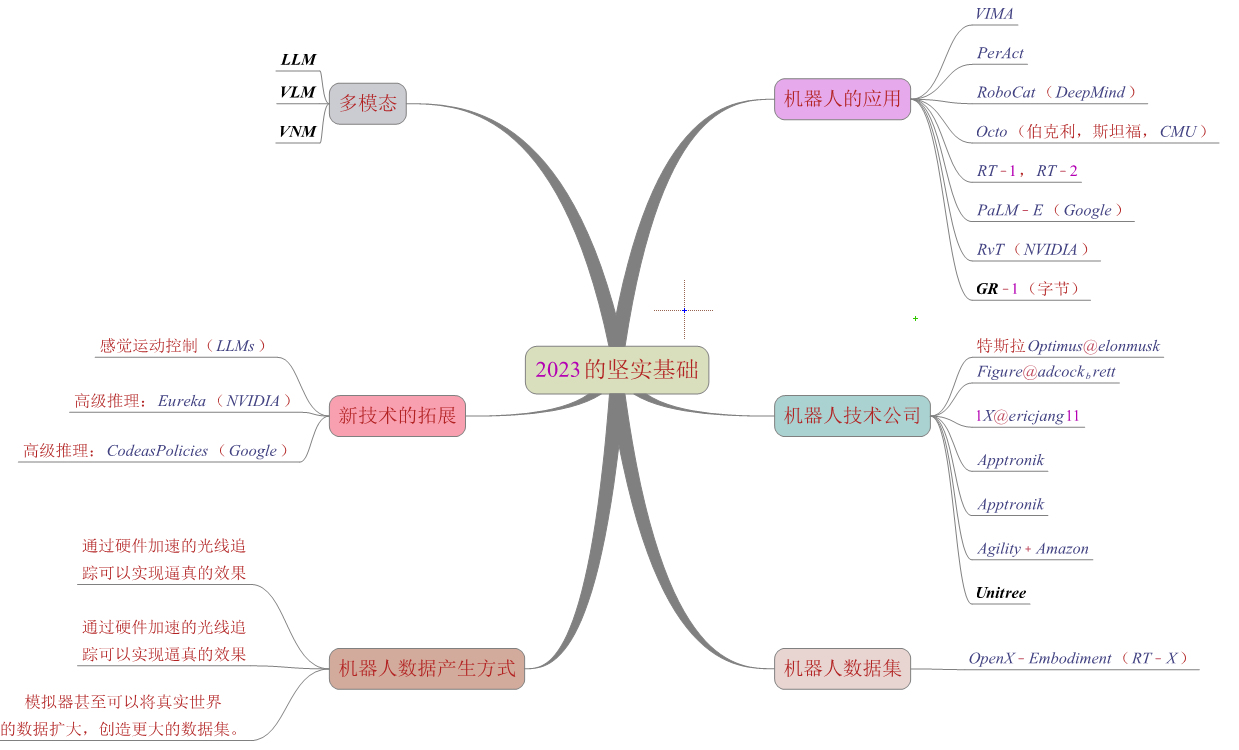
2023机器人行业总结,2024机器人崛起元年(具身智能)
2023总结: 1.Chatgpt引爆了通用人工智能,最大的受益者或是机器人,2023年最热门的创业赛道便是人形机器人,优必选更是成为人形机器人上市第一股, 可以说2023年是机器人开启智能化的元年,而2024则将成为机器…...

go 语言中的类型判断
_. ok : interface{}(a).(B)此语句用于判断对象a是否是B类型 也可以判断对象a是否实现了B接口 package mainimport "fmt"type Pet interface {SetName(name string)Name() stringCategory() string } type Dog struct {name string }func (dog *Dog) SetName(name …...
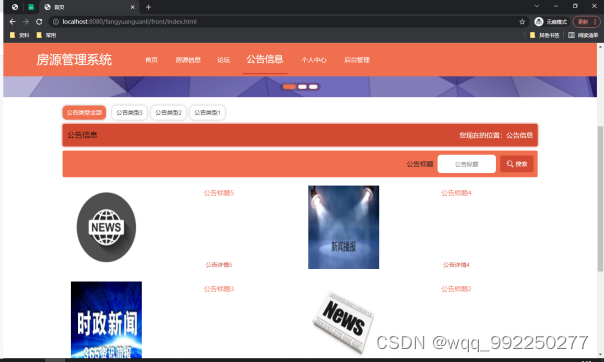
java基于ssm的房源管理系统+vue论文
目 录 目 录 I 摘 要 III ABSTRACT IV 1 绪论 1 1.1 课题背景 1 1.2 研究现状 1 1.3 研究内容 2 2 系统开发环境 3 2.1 vue技术 3 2.2 JAVA技术 3 2.3 MYSQL数据库 3 2.4 B/S结构 4 2.5 SSM框架技术 4 3 系统分析 5 3.1 可行性分析 5 3.1.1 技术可行性 5 3.1.2 操作可行性 5 3…...
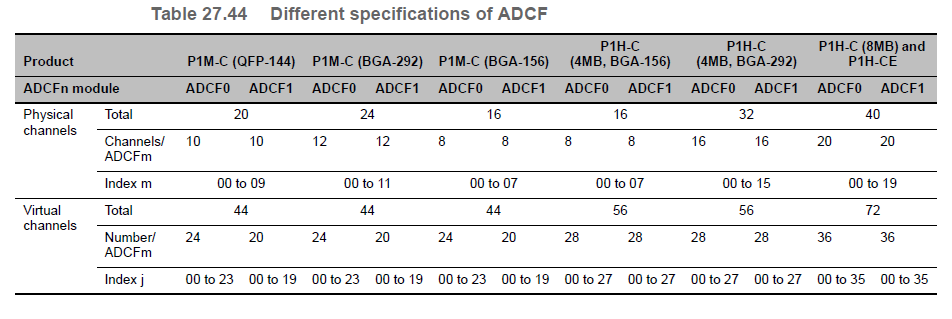
RH850P1X芯片学习笔记-A/D Converter (ADCF)
文章目录 Features of RH850/P1x-C ADCFNumber of UnitsRegister Base AddressClock SupplyInterrupts and DMAHardware ResetExternal Input/Output SignalsVirtual Channel OverviewFunctional OverviewBlock DiagramPhysical Channels, Virtual Channels and Scan Groups Re…...

38 调优kafka
操作系统调优 1.禁止atime更新,减少文件系统的写操作。 mount -o noatime 2.选择高性能的文件系统,如ext4或者XFS 3.swap空间设置,将swappniness设置成很小的一个值比如1~10,防止linux OOM Killer 开启随意杀掉进程。…...

java推荐系统:好友推荐思路
1.表的设计 表里面就两个字段,一个字段是用户id,另外一个字段是好友id,假如A跟B互为好友,那在数据库里面就会有两条数据 2.推荐好友思路 上面的图的意思是:h跟a的互为好友,a跟b,c&am…...

java: 写入数据到HBase
一、添加依赖 <dependency><groupId>org.apache.hadoop</groupId><artifactId>hadoop-client</artifactId><version>2.6.0</version></dependency><dependency><groupId>org.apache.hbase</groupId><art…...
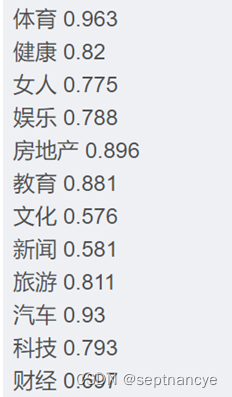
机器学习-基于Word2vec搜狐新闻文本分类实验
机器学习-基于Word2vec搜狐新闻文本分类实验 实验介绍 Word2vec是一群用来产生词向量的相关模型,由Google公司在2013年开放。Word2vec可以根据给定的语料库,通过优化后的训练模型快速有效地将一个词语表达成向量形式,为自然语言处理领域的应…...
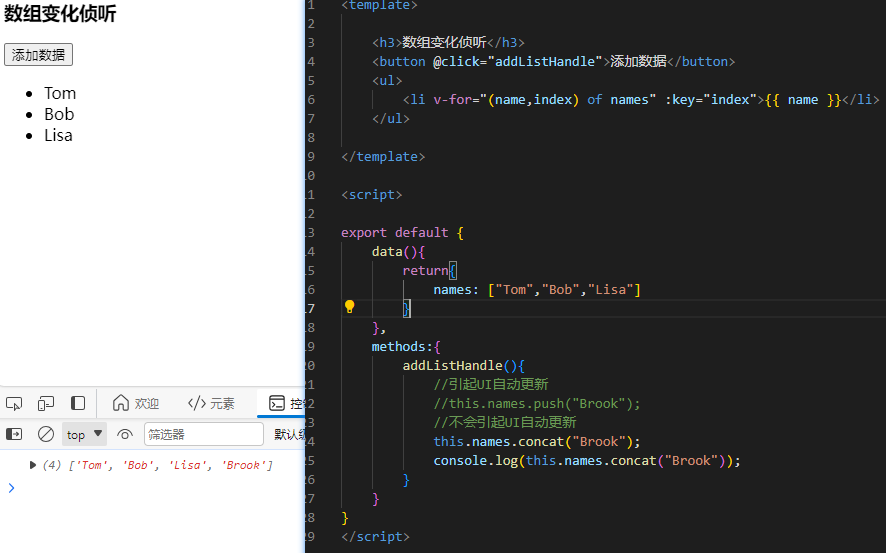
5.vue学习笔记(数组变化的侦测+计算属性+Class绑定)
文章目录 1.数组变化的侦测1.1.变更方法1.2.替换一个数组 2.计算属性计算属性缓存vs方法 3.Class绑定3.1.绑定对象3.2.多个对象的绑定形式3.3.绑定数组3.4.数组与对象 1.数组变化的侦测 1.1.变更方法 vue能够侦听响应式数组的变更方法,并在它们被调用时出发相关的…...

Java十种经典排序算法详解与应用
数组的排序 前言 排序概念 排序是将一组数据,依据指定的顺序进行排列的过程。 排序是算法中的一部分,也叫排序算法。算法处理数据,而数据的处理最好是要找到他们的规律,这个规律中有很大一部分就是要进行排序,所以需…...

git常用命令及概念对比
查看日志 git config --list 查看git的配置 git status 查看暂存区和工作区的变化内容(查看工作区和暂存区有哪些修改) git log 查看当前分支的commit 记录 git log -p commitID详细查看commitID的具体内容 git log -L :funcName:fileName 查看file…...

57、python 环境搭建[for 计算机视觉从入门到调优项目]
从本节开始,进入到代码实战部分,在开始之前,先简单进行一下说明。 代码实战部分,我会默认大家有一定的编程基础,不需要对编程很精通,但是至少要会 python 的基础语法、python 环境搭建、pip 的使用;C++ 要熟悉基础知识和基础语法,会根据文章中的步骤完成 C++ 的环境搭…...
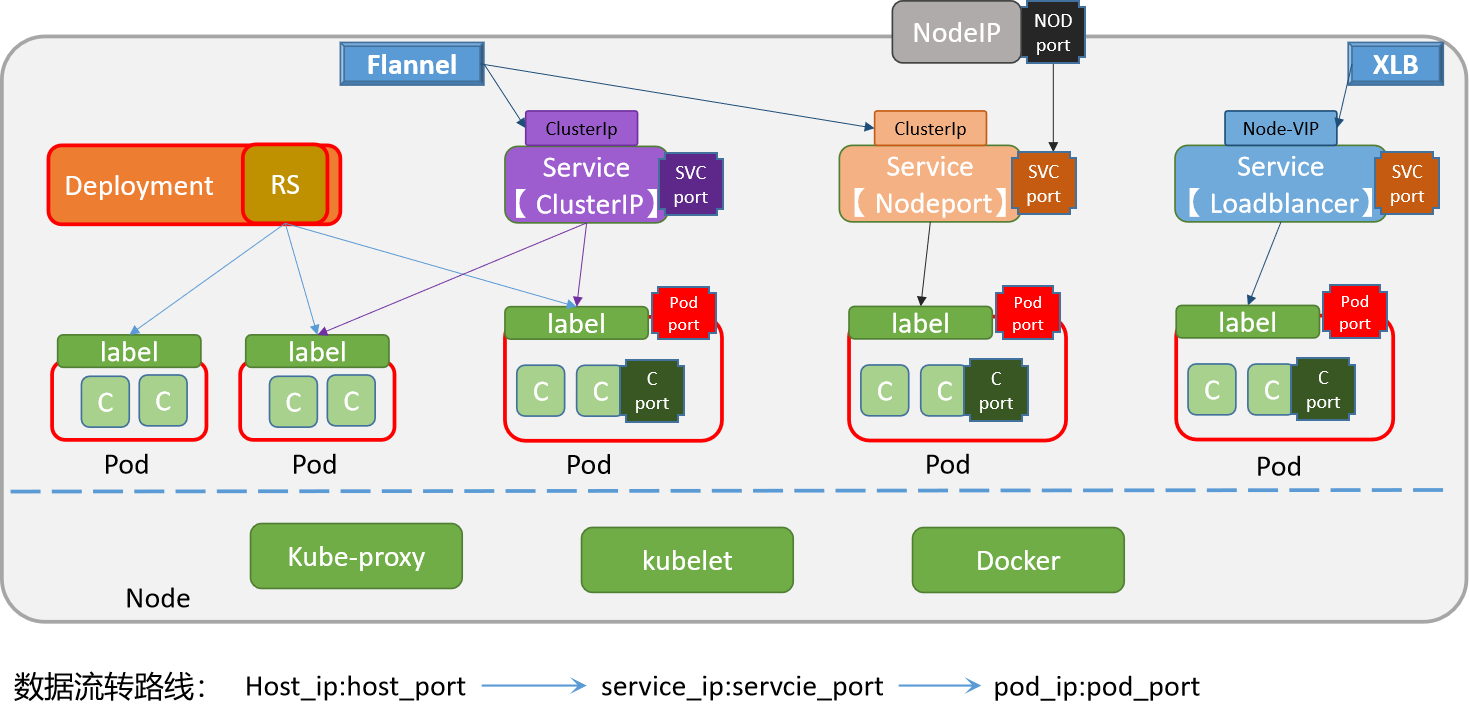
K8S-应用访问
1 service对象定位 2 Service 实践 手工创建Service 根据应用部署资源对象,创建SVC对象 kubectl expose deployment nginx --port80 --typeNodePortyaml方式创建Service nginx-web的service资源清单文件 apiVersion: v1 kind: Service metadata:name: sswang-ngi…...
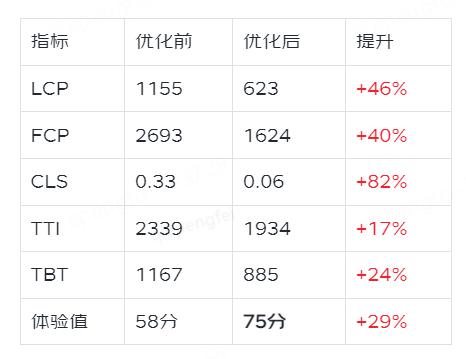
商智C店H5性能优化实战
前言 商智C店,是依托移动低码能力搭建的一个应用,产品面向B端商家。随着应用体量持续增大,考虑产品定位及用户体验,我们针对性能较差页面做了一次优化,并取得了不错的效果,用户体验值(UEI&…...

Unity 使用 Plastic 同步后,正常工程出现错误
class Newtonsoft.Json.Linq.JToken e CS0433:类型"JToken"同时存在于"Newtonsoft.Json.Net20,Version3.5.0.0,Cultureneutral,,PublicKeyToken30ad4fe6b2a6aeed"和"Newtonsoft.Json, Version12.0.0.0,Cultureneutral,PublicKeyToken30ad4fe6b2a6aeed…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
