当前位置：首页 > news >正文

概率论与数理统计知识点+课后习题

news 2025/12/15 9:49:48

文章目录

💖 [学习资源整合](https://www.cnblogs.com/duisheng/p/17872980.html)
📚 总复习
- 📙 选择题
- 📙 填空题
- 📙 大题
- - 1. 概率
  - 2. 概率
  - 3. 概率
  - 4. P
  - 5. 概率
  - 6. 概率密度函数 $F (X)$
  - 7. 分布列求方差 $V (X)$
  - 8. 求分布函数 $F (X)$
💖 速成课
- 一、事件的概率
- - 1. 无放回类题目
  - 2. 有放回类的题目
  - 3. 需要画图的题目
  - 4. 条件概率
  - 5. 全概率公式
  - 6. 贝叶斯公式
- 二、一维随机变量
- - 1. $F (x) 和 f (x)$ 知一求二
  - 2. $F (x) 和 f (x)$ 知一求 $P$
  - 3. $F (x) 和 f (x)$ 含未知数，求未知数
  - 4. 求分布律
  - 5. 已知含有未知数的分布列，求未知数
- 三、一维随机变量函数
- - 1. 已知 X 分布列，求 Y 分布列
  - 2. 已知 $F_X (x)$ ，求 $F_Y (y)$
  - 3. 已知 $f_X (x)$ ，求 $f_Y (y)$
- 四、五种常见的分布
- - 1. 均匀分布
  - 2. 泊松分布
  - 3. 二项分布
  - 4. 指数分布
  - 5. 正态分布
  - 6. 正态分布图像
- 五、二维随机变量
- - 1. 二维离散型分布律求概率
  - 2. 二维离散型分布律求独立性
  - 3. 知 $F (x, y)$ 求 $f (x, y)$
  - 4. 知 $f (x, y)$ 求 $F (x, y)$
  - 5. 已知 $F (x, y)$ 求 $P$
  - 6. 已知 $f (x, y)$ 求 $P$
  - 7. 已知 $F (x, y)$ 或 $f (x, y)$ 含有的未知数
  - 8. 求均匀分布的 $f (x, y)$ 与 $P$
- 六、期望与方差
- 七、中心极限定理
- 八、抽样分布

📚 总复习

📙 选择题

在这里插入图片描述

📙 填空题

在这里插入图片描述

📙 大题

1. 概率

在这里插入图片描述

2. 概率

在这里插入图片描述

3. 概率

在这里插入图片描述

4. P

在这里插入图片描述

5. 概率

在这里插入图片描述

6. 概率密度函数 $F (X)$

在这里插入图片描述

7. 分布列求方差 $V (X)$

在这里插入图片描述

8. 求分布函数 $F (X)$

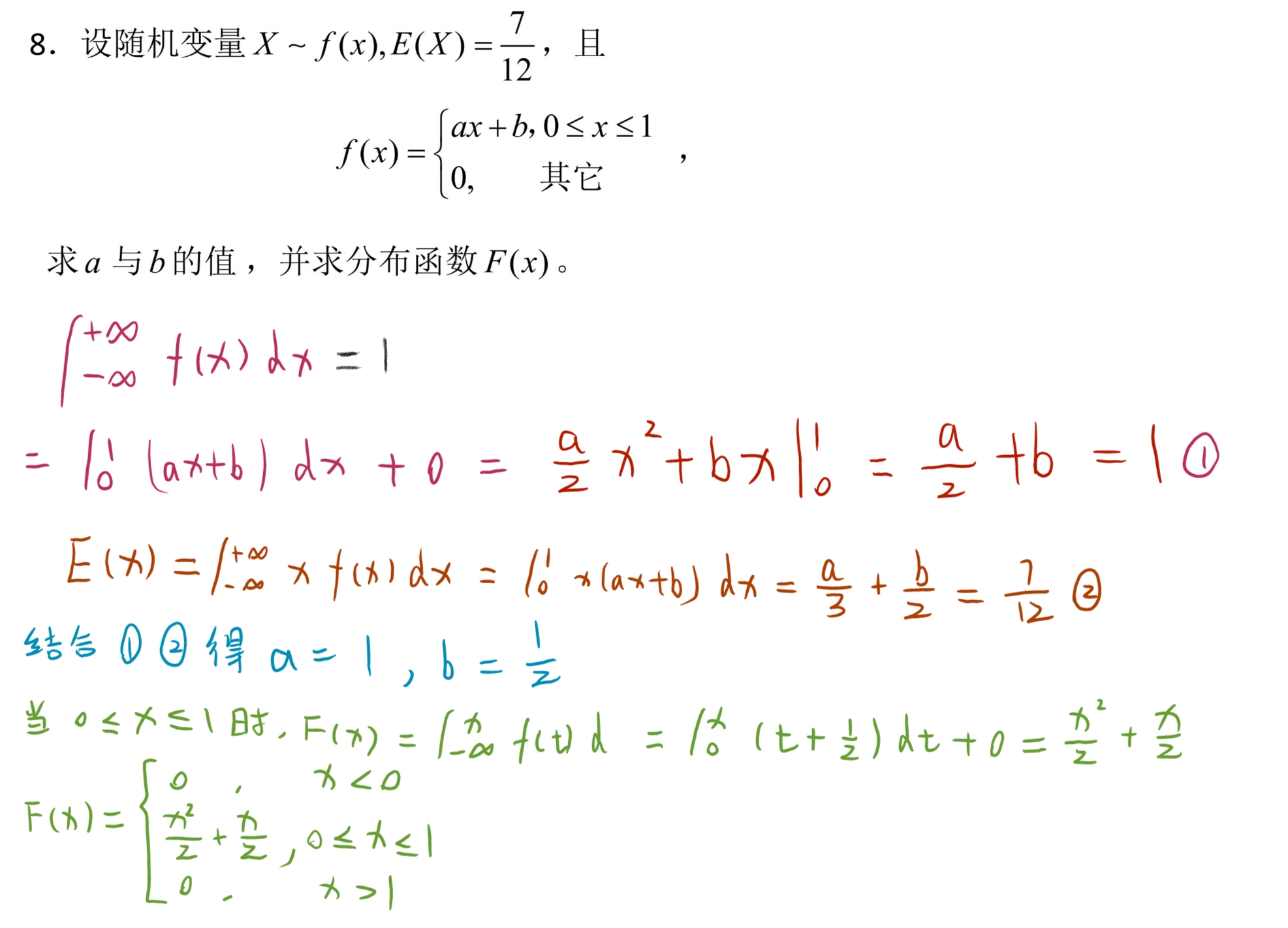
在这里插入图片描述

💖 速成课

一、事件的概率

1. 无放回类题目

在这里插入图片描述

2. 有放回类的题目

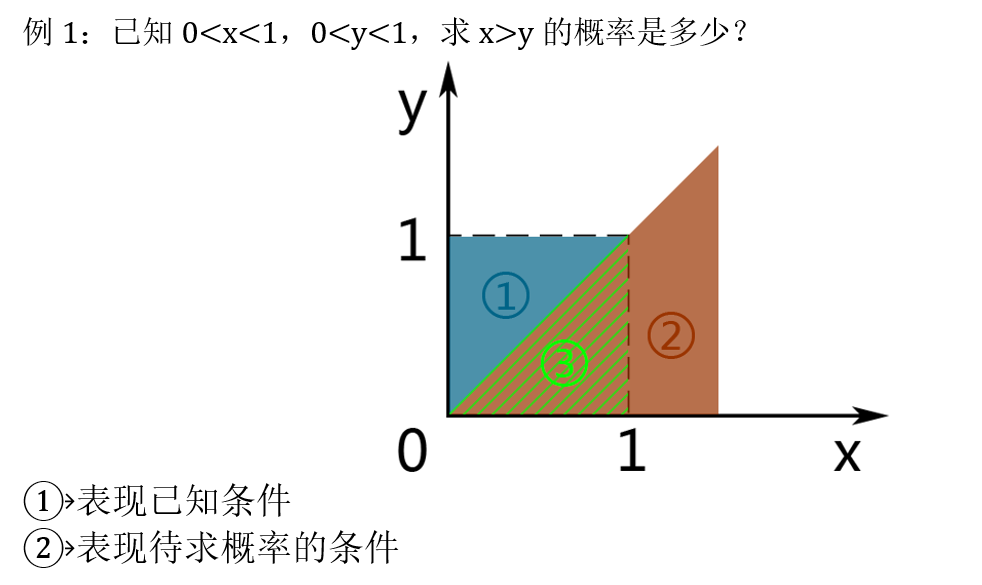
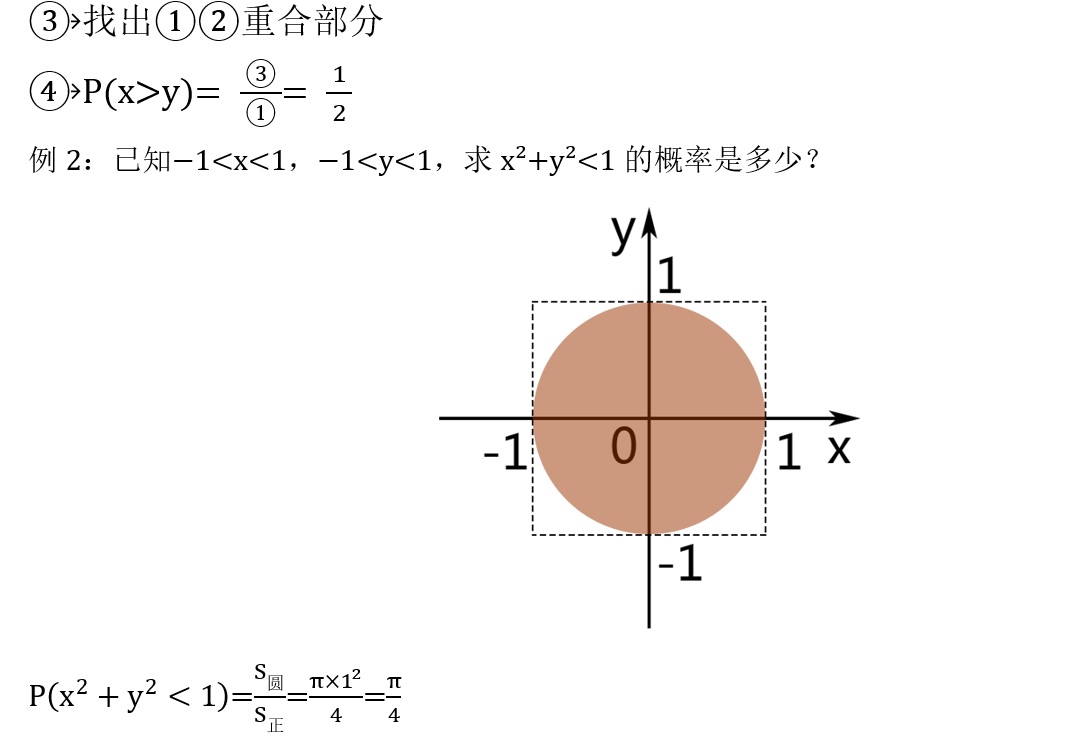
在这里插入图片描述

3. 需要画图的题目

在这里插入图片描述

4. 条件概率

在这里插入图片描述

5. 全概率公式

在这里插入图片描述

6. 贝叶斯公式

在这里插入图片描述

二、一维随机变量

1. $F (x) 和 f (x)$ 知一求二

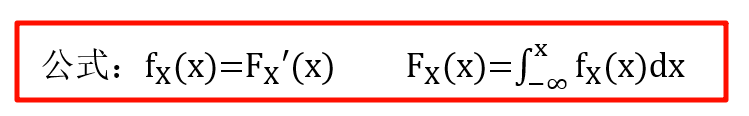
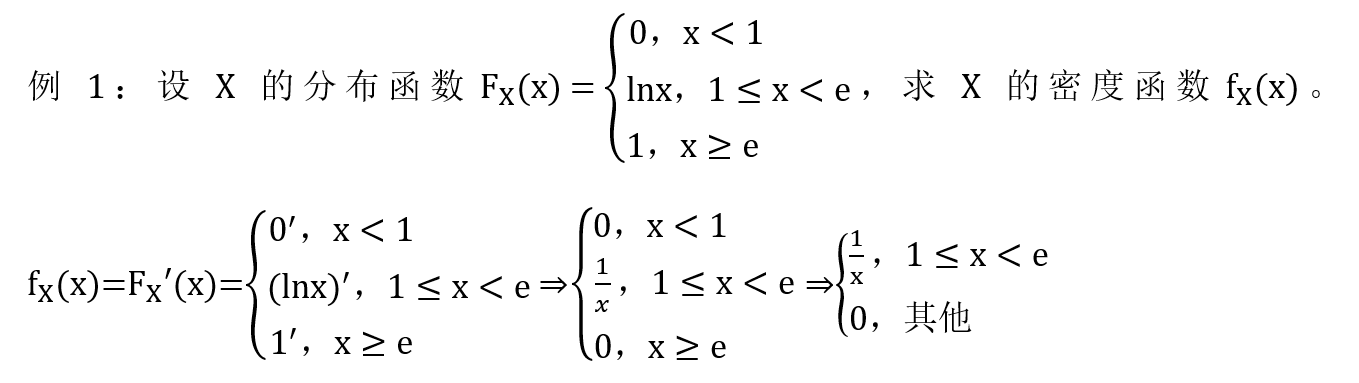
在这里插入图片描述

2. $F (x) 和 f (x)$ 知一求 $P$

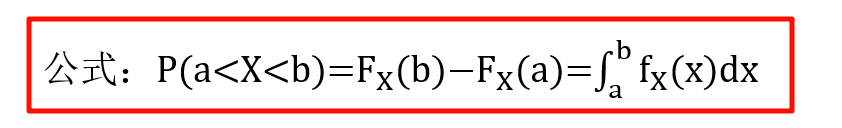
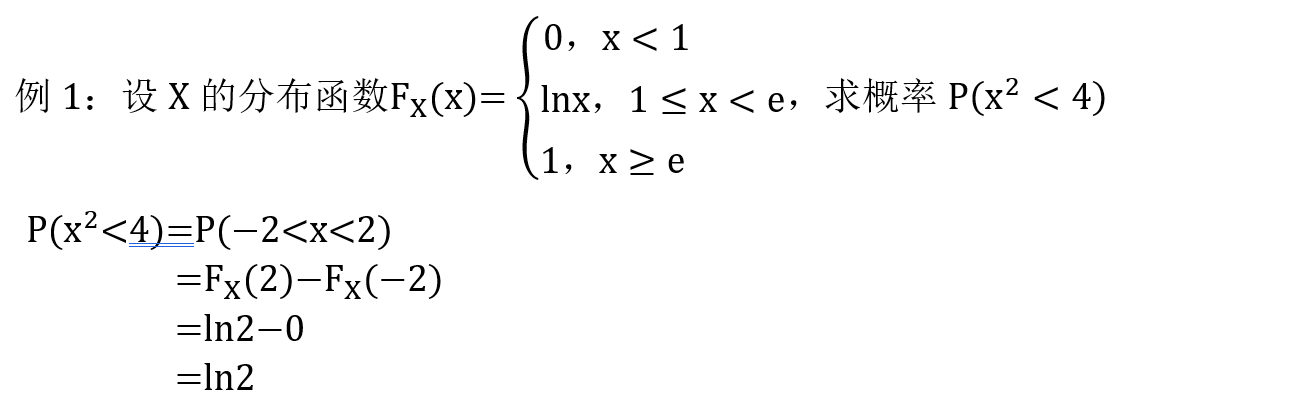
在这里插入图片描述

3. $F (x) 和 f (x)$ 含未知数，求未知数

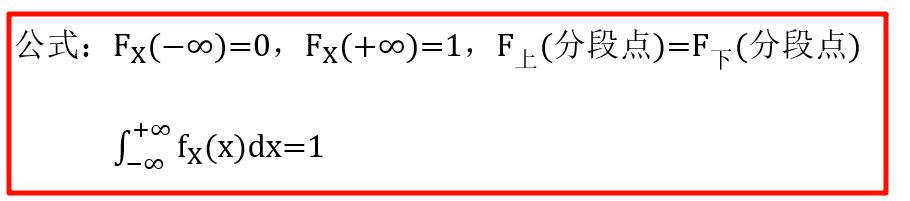
在这里插入图片描述

4. 求分布律

在这里插入图片描述

5. 已知含有未知数的分布列，求未知数

在这里插入图片描述

三、一维随机变量函数

1. 已知 X 分布列，求 Y 分布列

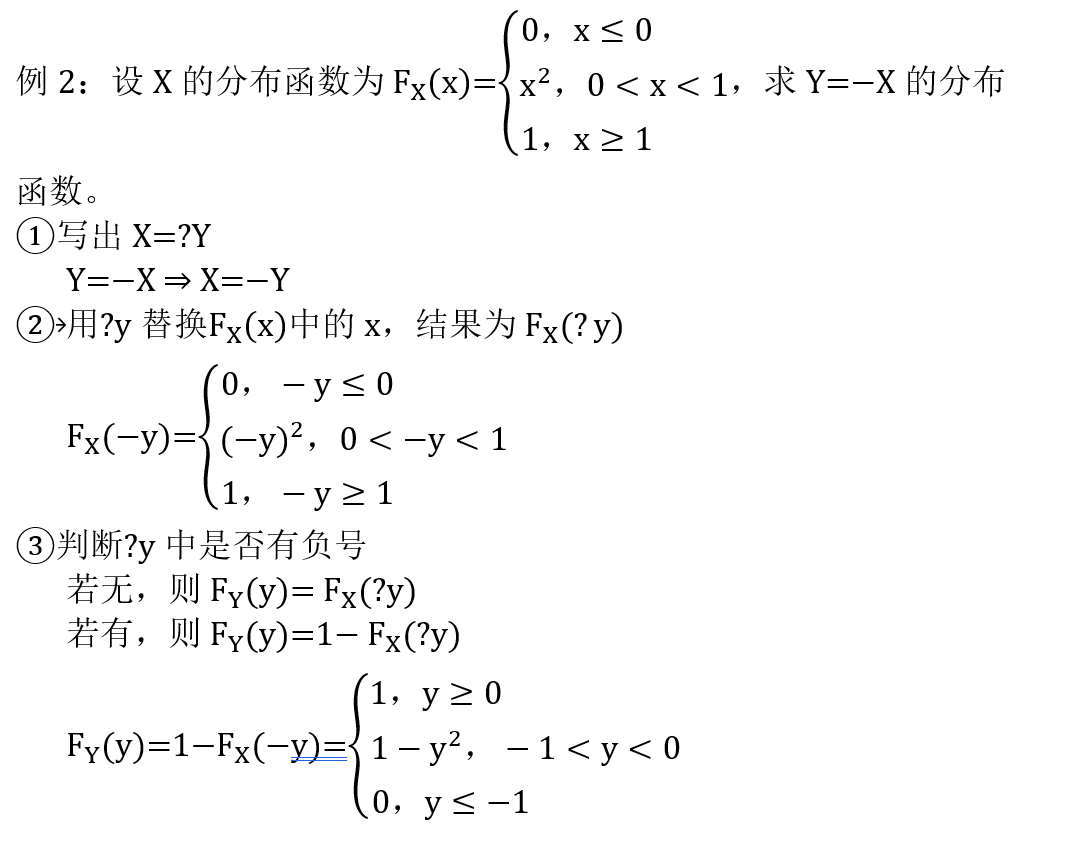
在这里插入图片描述

2. 已知 $F_X (x)$ ，求 $F_Y (y)$

在这里插入图片描述

3. 已知 $f_X (x)$ ，求 $f_Y (y)$

在这里插入图片描述

四、五种常见的分布

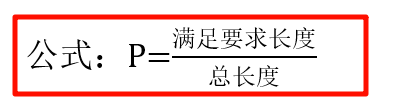
在这里插入图片描述

1. 均匀分布

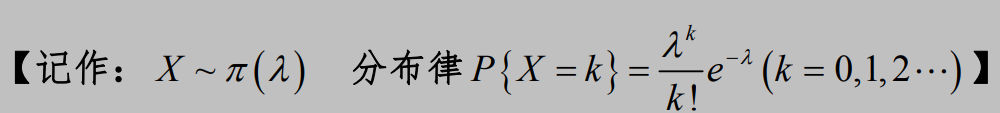
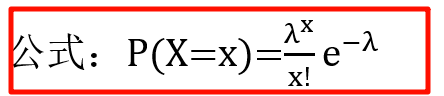
在这里插入图片描述

2. 泊松分布

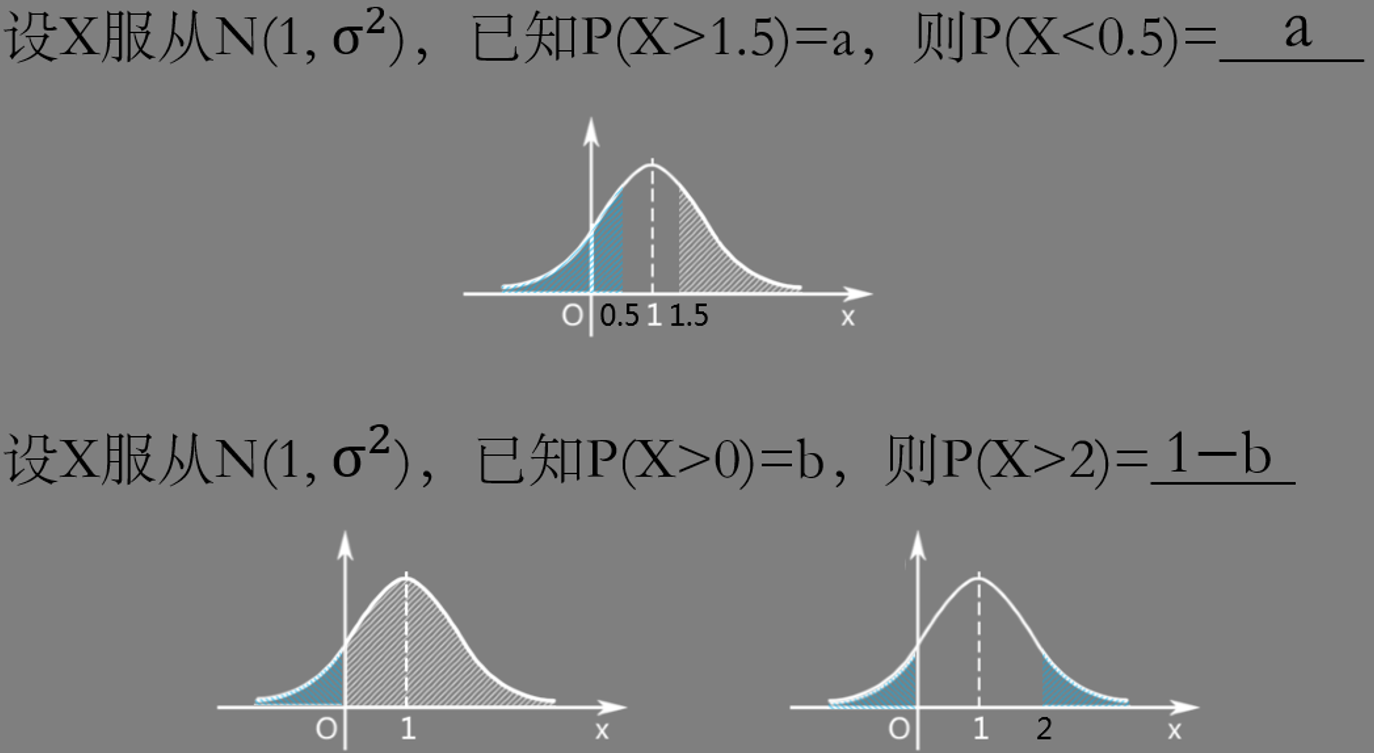
在这里插入图片描述

3. 二项分布

在这里插入图片描述

4. 指数分布

在这里插入图片描述

5. 正态分布

在这里插入图片描述

6. 正态分布图像

在这里插入图片描述

五、二维随机变量

1. 二维离散型分布律求概率

在这里插入图片描述

2. 二维离散型分布律求独立性

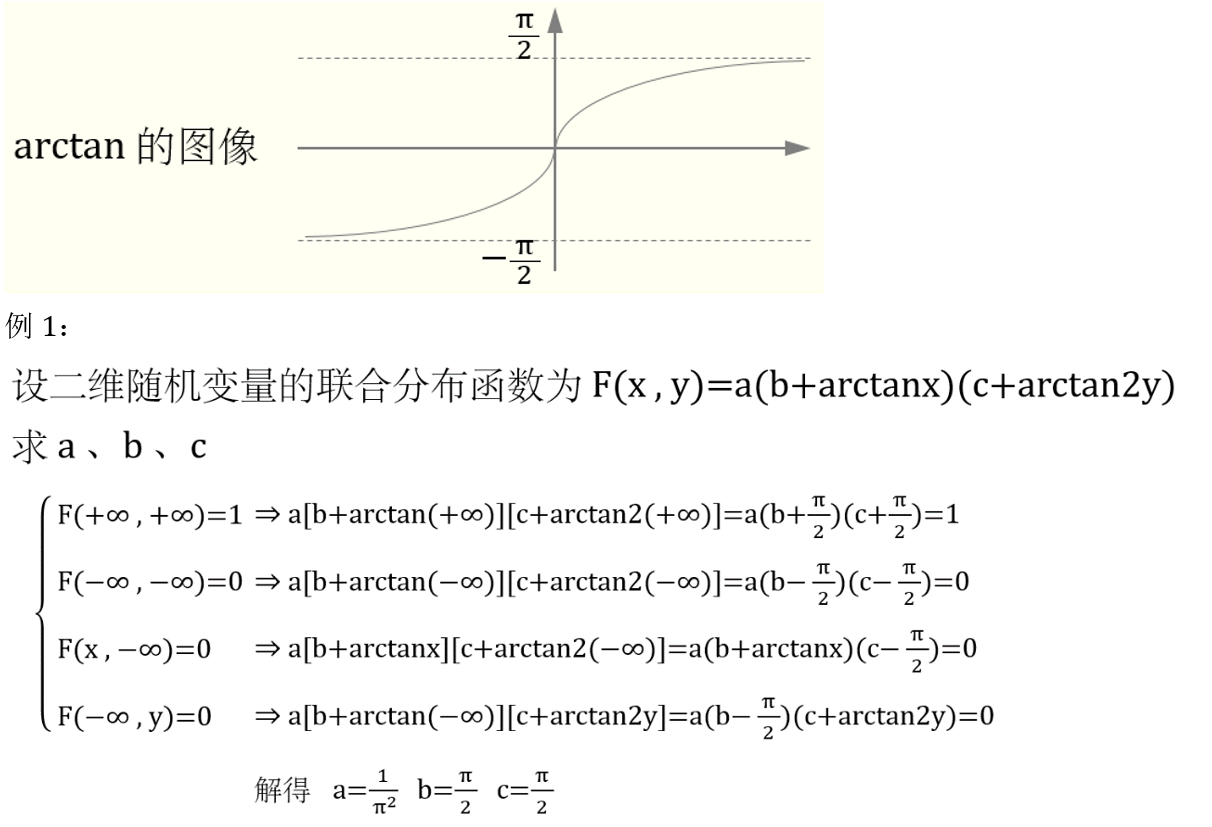
在这里插入图片描述

3. 知 $F (x, y)$ 求 $f (x, y)$

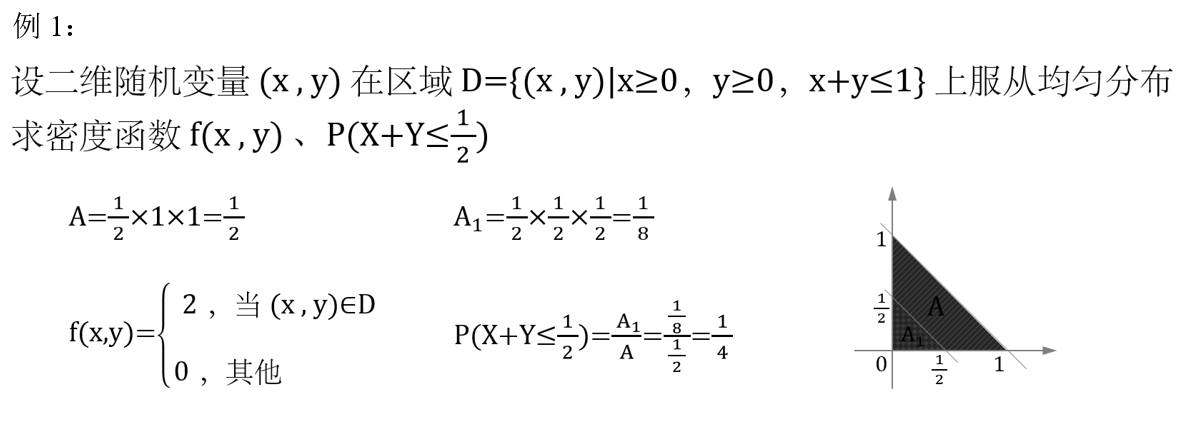
在这里插入图片描述

4. 知 $f (x, y)$ 求 $F (x, y)$

在这里插入图片描述

5. 已知 $F (x, y)$ 求 $P$

在这里插入图片描述

6. 已知 $f (x, y)$ 求 $P$

在这里插入图片描述

7. 已知 $F (x, y)$ 或 $f (x, y)$ 含有的未知数

在这里插入图片描述

8. 求均匀分布的 $f (x, y)$ 与 $P$

在这里插入图片描述

六、期望与方差

1. 离散型的期望 $E (x)$

在这里插入图片描述

2. 连续型的期望 $E (X)$

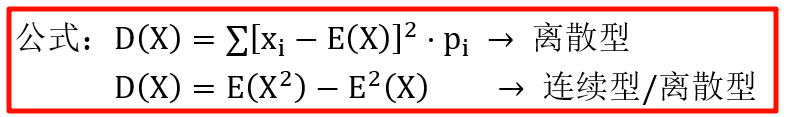
在这里插入图片描述

3. $Y = g (x)$ 求 $E (Y)$

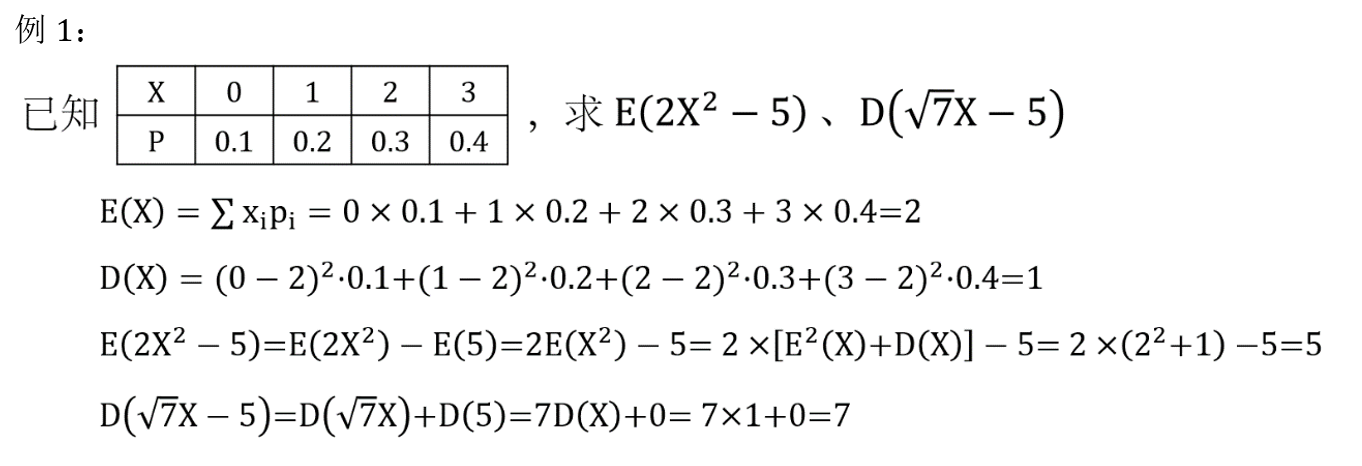
在这里插入图片描述

4. 方差 $D (X)$

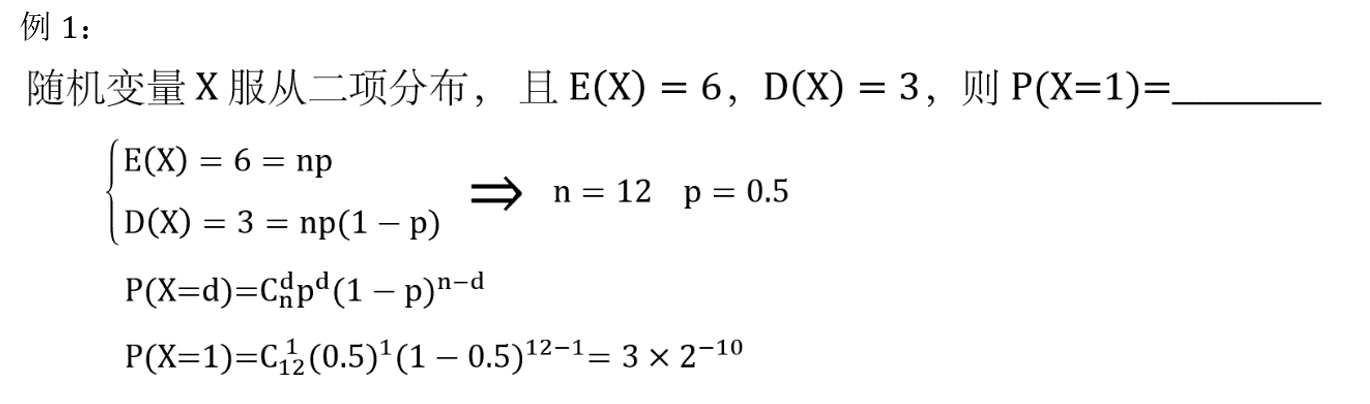
在这里插入图片描述
例1

在这里插入图片描述

5. 根据 $E (X) 、 D (X)$ 的性质进行复杂运算 ⭐

在这里插入图片描述

6. $E (X) 、 D (X)$ 与各种分布的综合题 ⭐

在这里插入图片描述

七、中心极限定理

在这里插入图片描述

八、抽样分布

概率论与数理统计知识点+课后习题

文章目录 💖 [学习资源整合](https://www.cnblogs.com/duisheng/p/17872980.html)📚 总复习📙 选择题📙 填空题📙 大题1. 概率2. 概率3. 概率4. P5. 概率6. 概率密度函数 F ( X ) F(X) F(X)7. 分布列求方差 V ( X ) …...

编程日记 2024/1/7 14:25:04

Spring Boot实战：深入理解@Service与@Mapper注解

1. Service 注解 Service 是Spring框架提供的一个注解，用于标记类为业务逻辑层的组件。当类上标注了Service注解后，Spring容器会自动扫描并创建该类的一个实例（即Bean），这样我们就可以在其他地方通过自动装配&#xf…...

编程日记 2024/1/7 14:23:03

【DevOps-06】Jenkins实现CI/CD操作

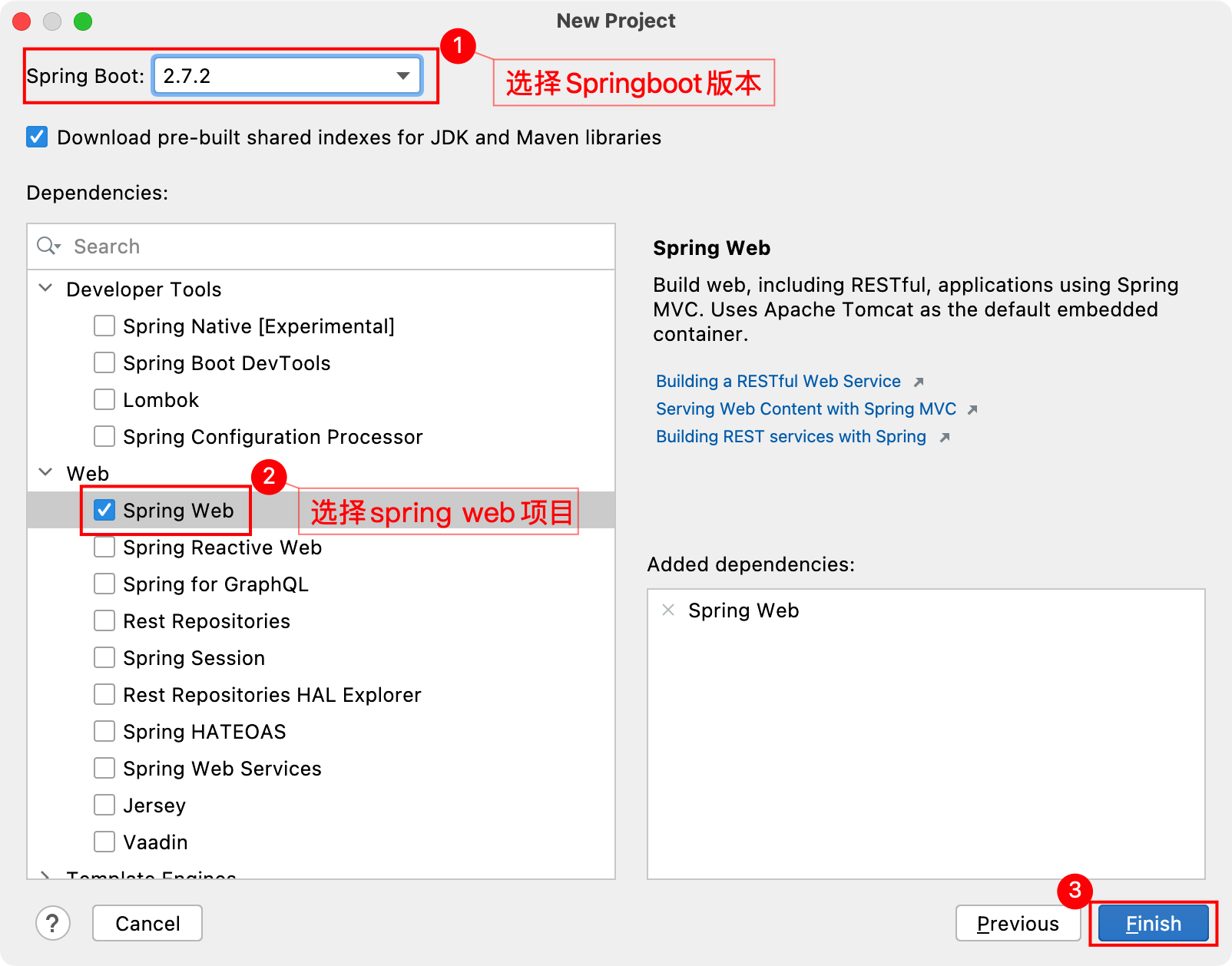
一、简要说明基于Jenkins拉取GitLab的SpringBoot代码进行构建发布到测试环境实现持续集成基于Jenkins拉取GitLab指定发行版本的SpringBoot代码进行构建发布到生产环境实现CD实现持续部署二、准备Springboot工程 1、IDEA新建工程 2、填写项目工程信息 3、选择Springboot版本…...

编程日记 2024/1/7 14:22:02

华为面经总结

为了帮助大家更好的应对面试，我整理了往年华为校招面试的题目，供大家参考~ 面经1 技术一面自我介绍说下项目中的难点volatile和synchronized的区别， 问的比较细大顶堆小顶堆怎么删除根节点CSRF攻击是什么，怎么预防线程通信方式…...

编程日记 2024/1/7 14:17:58

大模型实战营Day1 书生·浦语大模型全链路开源体系

1.大模型为发展通用人工智能的重要途经专用模型：针对特定任务解决特定问题通用大模型：一个模型对应多模态多任务 2.InternLM大模型开源历程 3.InternLM-20B大模型性能 4.从模型到应用：智能客服、个人助手、行业应用 5.书生浦语全链条开源…...

编程日记 2024/1/7 14:15:56

Java 集合面试题真实场景还原

Java 集合面试题真实场景还原文章目录 Java 集合面试题真实场景还原Java常见的集合类ListHashMap Java常见的集合类面试官：说一说Java提供的常见集合？（画一下集合结构图） 候选人： 嗯~~，好的。在java中提…...

编程日记 2024/1/7 14:13:54

AutoSAR（基础入门篇）4.9-Autoar_BSW小结

Autoar_BSW小结 Autoar_BSW小结一、Autoar_BSW小结 1、BSW组件图 2、BSW的功能概述 3、BSW在工程里的应用实际工程...

编程日记 2024/1/7 14:11:52

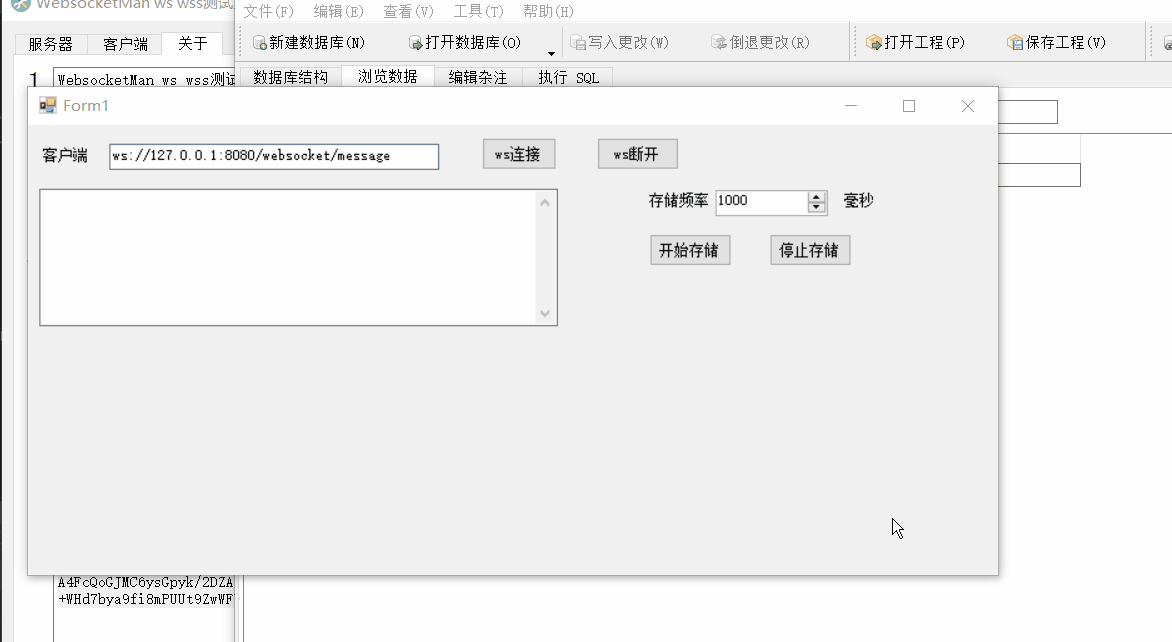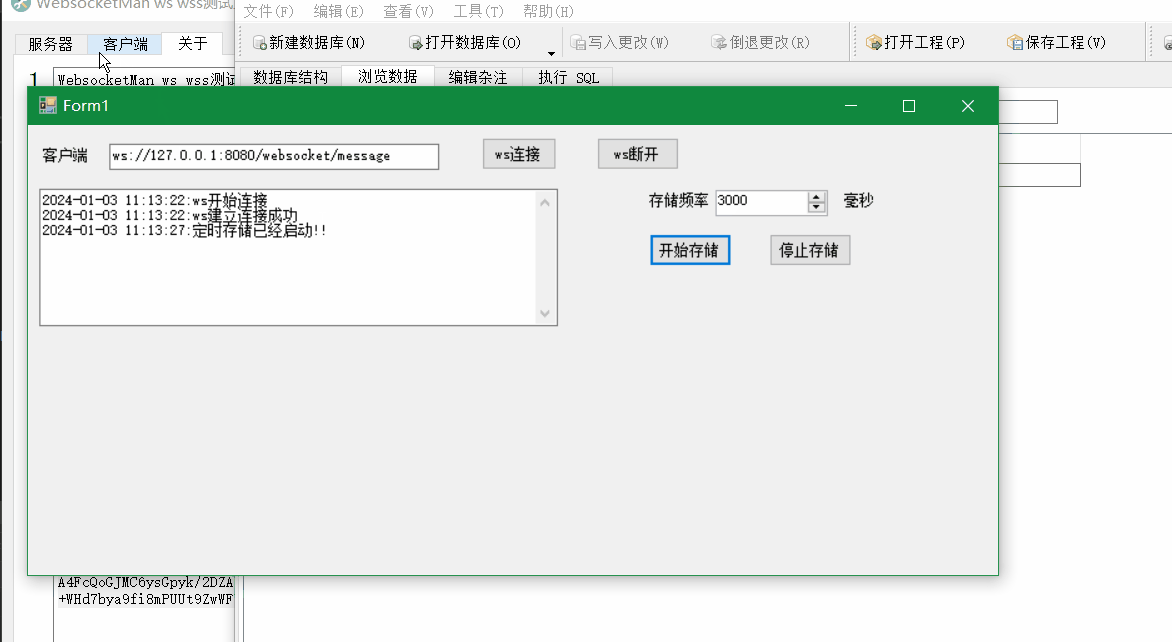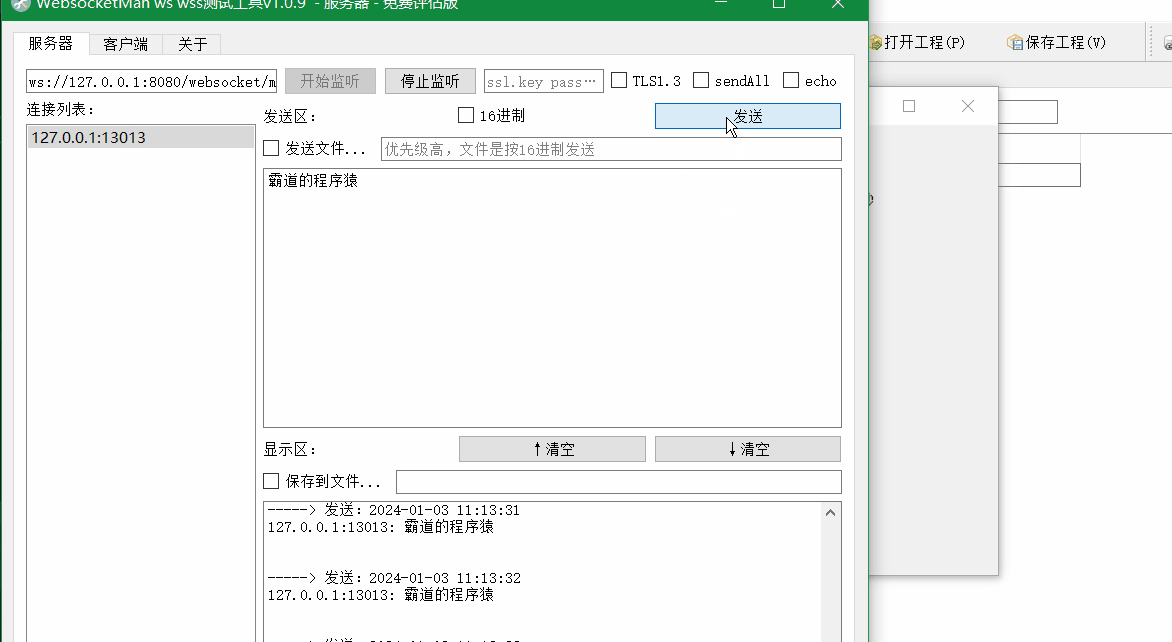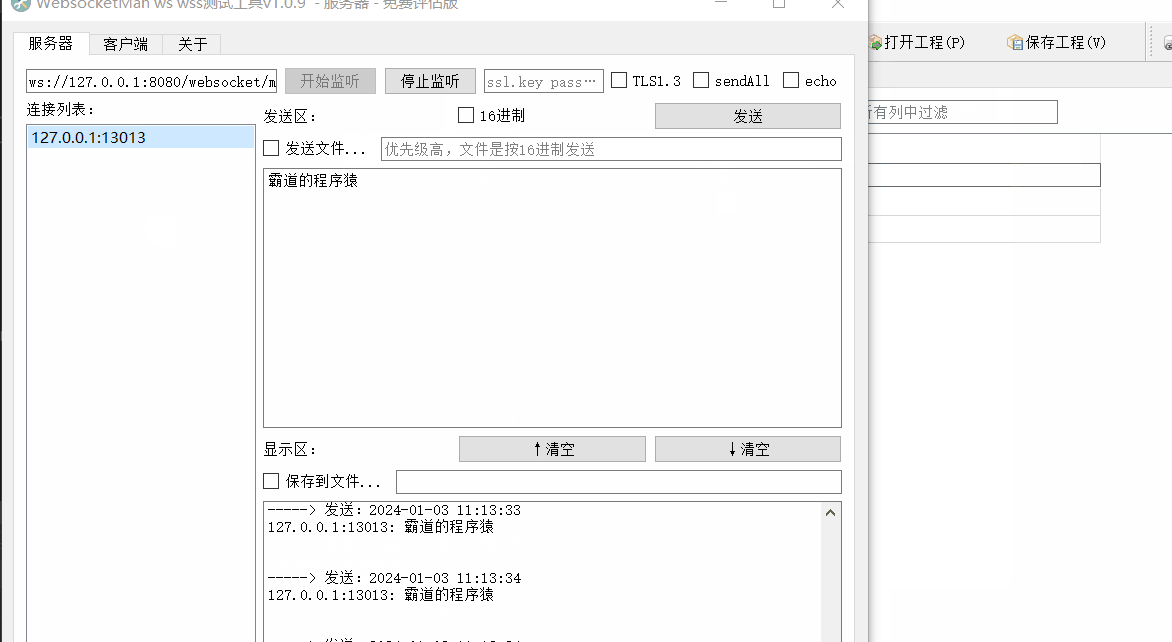
Winform中使用Websocket4Net实现Websocket客户端并定时存储接收数据到SQLite中

场景 SpringBootVue整合WebSocket实现前后端消息推送： SpringBootVue整合WebSocket实现前后端消息推送_websocket vue3.0 springboot 往客户端推送-CSDN博客上面实现ws推送数据流程后，需要在windows上使用ws客户端定时记录收到的数据到文件中&#x…...

编程日记 2024/1/7 14:06:48

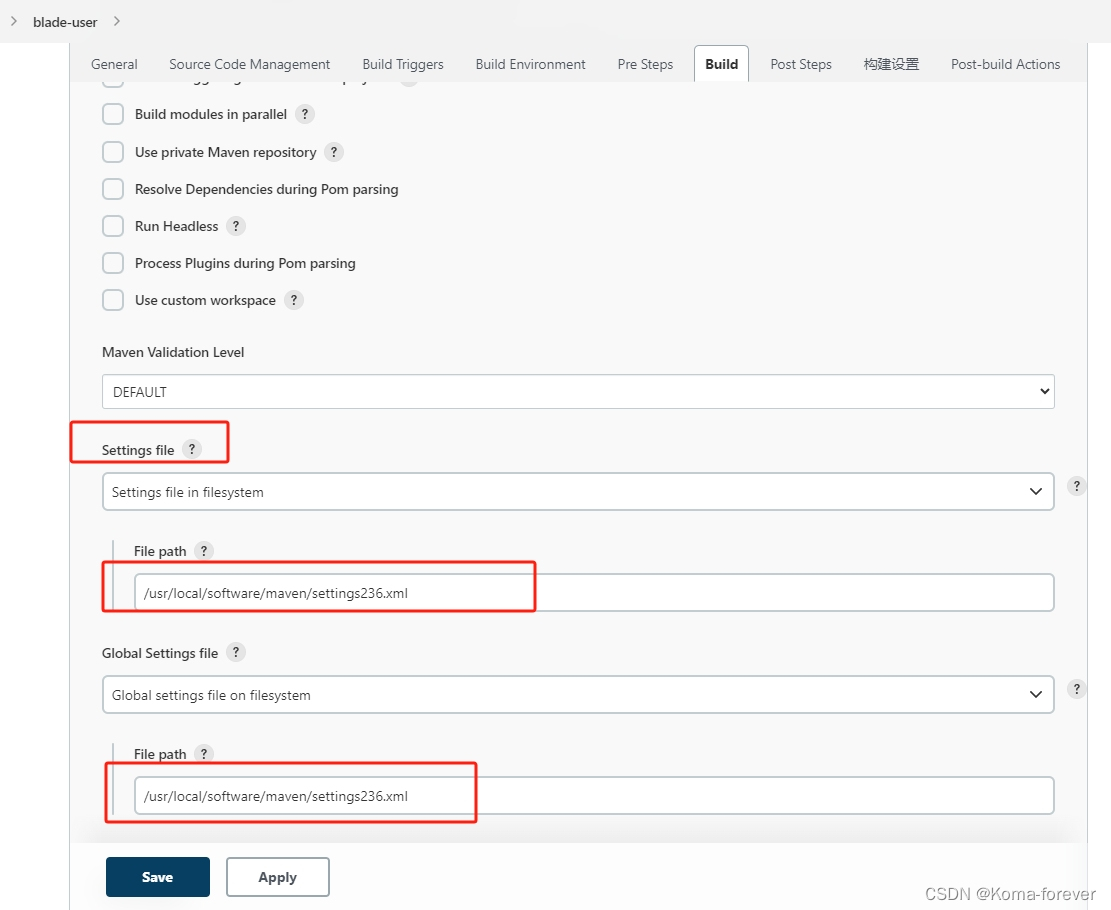
Jenkins修改全局maven配置后不生效解决办法、以及任务读取不同的settings.xml文件配置

一、修改Global Tool Configuration的maven配置不生效说明：搭建好jenkins后，修改了全局的settings.xml，导致读取settings一直是之前配置的。解决办法一 Jenkins在创建工作任务时，会读取当前配置文件内容，固定在这…...

编程日记 2024/1/7 14:05:47

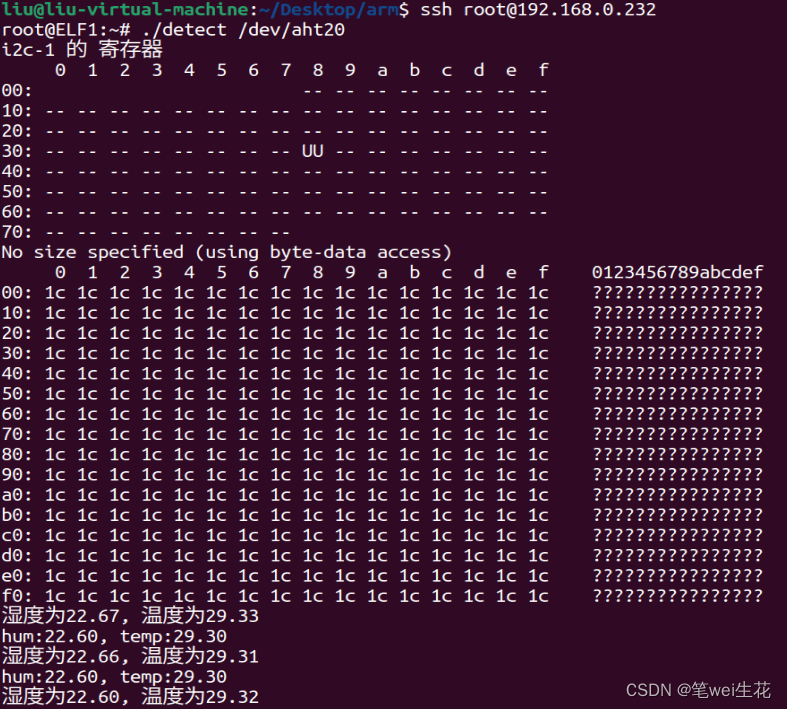
【elfboard linux开发板】7.i2C工具应用与aht20温湿度寄存器读取

1. I2C工具查看aht20的温湿度寄存器值 1.1 原理图传感器通过IIC方式进行通信，连接的为IIC1总线，且设备地址为0x38，实际上通过后续iic工具查询，这个设备是挂载在iic-0上 1.2 I2C工具通过i2c工具可以实现查询i2c总线、以及上面…...

编程日记 2024/1/7 14:02:44

LeetCode-有效的字母异位词（242）

题目描述： 给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。注意：若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词。思路： 这题还是比较简单的，首先将两个字符…...

编程日记 2024/1/7 14:01:43

【AIGC-图片生成视频系列-6】SSR-Encoder：用于主题驱动生成的通用编码器

目录一. 贡献概述二. 方法详解 a) 训练阶段 b) 推理生成阶段： 三. 综合结果四. 注意力可视化五. 选择性主题驱动图像生成六. 人体图像生成七. 可推广到视频生成模型八. 论文九. 个人思考稳定扩散（Stable Diffusion）模型可…...

编程日记 2024/1/7 13:59:42

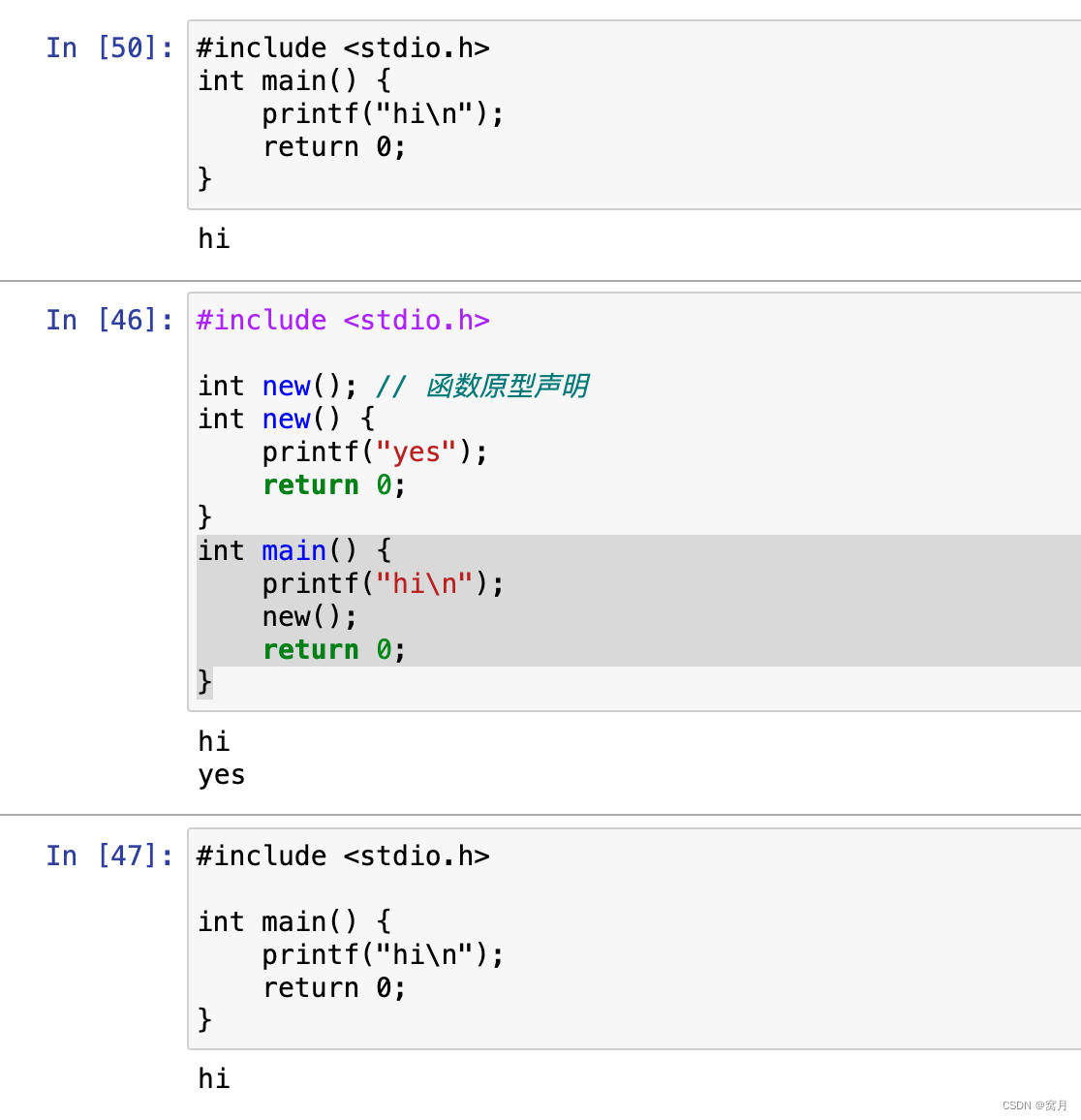
[C]jupyter中使用C

[C]jupyter中使用C 安装使用用处安装 https://github.com/brendan-rius/jupyter-c-kernel 下拉找到3条命令，装就可以了 mac和linux可用 python3可用， 2不可以第二条命令可以改为 : python3 install_c_kernel 小总结：如果有问题&#xff0…...

编程日记 2024/1/7 13:56:39

探讨一下WebINFO 下的一些思考

在平时的开发中，我们经常看到一个/WEB-INF 这个目录，这个是web 容器初始化加载的一个标准路径。官方解释：WEB-INF 是 Java 的 web 应用的安全目录。所谓安全就是客户端无法访问，只有服务端可以访问的目录。也就是说，这…...

编程日记 2024/1/7 13:55:38

MySQL中的开发基于Python的SQL工具类操作数据库简单示例

操作数据库封装SQL工具类的两种方式为了更方便的实现基于连接池和pymysql 连接数据库，需开发一个sql工具类来让sql操作更简洁用两张方式来封装SQL工具类 1 ）单例模式封装 db.py 工具类 import pymysql from dbutils.pooled_db import PooledDBclas…...

编程日记 2024/1/7 13:52:36

安卓Android Studio读写FM1208CPU卡源码

本示例使用的发卡器：https://item.taobao.com/item.htm?spma1z10.5-c-s.w4002-21818769070.11.6c46789elLwMzv&id615391857885 <?xml version"1.0" encoding"utf-8"?> <androidx.constraintlayout.widget.ConstraintLayout x…...

编程日记 2024/1/7 13:51:35

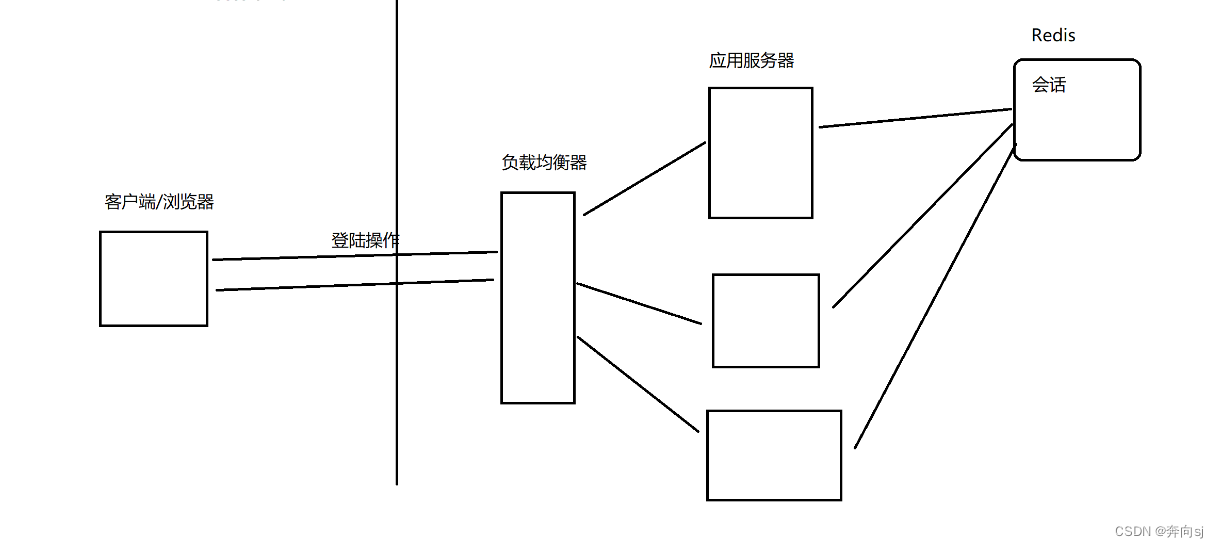
二、Redis的特性与应用场景

Redis是一个在内存中存储数据的中间件，主要用于作为数据库、数据缓存，在分布式系统中有着非常重要的地位。面试中可以围绕Redis的特性进行介绍。一、Redis特性 1、在内存中存储数据 MySQL主要是“表”的方式来存储组织数据的，是“关系型数…...

编程日记 2024/1/7 13:43:27

编程笔记 html5cssjs 019 HTML实体

编程笔记 html5&css&js 019 HTML实体一、HTML 字符实体二、HTML 符号实体小结在HTML文档中，用一些标记表示特定的格式，那我们想使用这些标记字符本身时就出了问题，直接使用时，会被浏览器解析为标记的，要想显…...

编程日记 2024/1/7 13:39:22

数据结构：树详解

创建二叉树给出了完整的先序遍历序列，子树为空用’#’表示，所以这样我们在通过先序遍历序列创建二叉树时我们直到先序遍历序列是先进行根结点，然后左子树最后右子树的顺序进行遍历的，所以对于完整的先序遍历序列我们可以直到先序…...

编程日记 2024/1/7 13:37:20

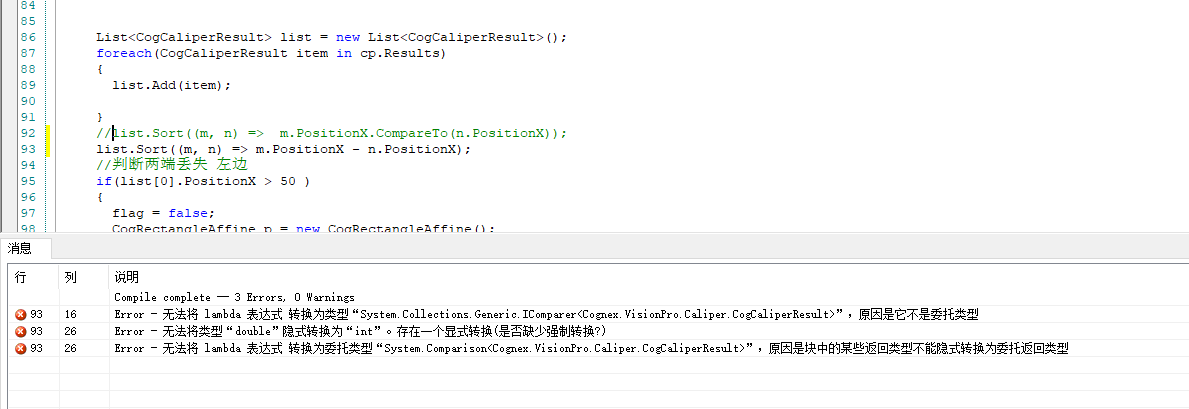
list1.Sort((m, n) =＞ m.Id - n.Id)； id是double类型的为什么回报错

问题产生的地方原因对于 double 类型的属性，不能直接使用减法运算符进行比较。减法运算符只能用于数值类型，而 double 是浮点数类型。要在 double 属性上进行排序，可以使用 CompareTo 方法或者使用自定义的比较器。更改要在 double 属性…...

编程日记 2024/1/7 13:33:17

conda相比python好处

Conda 作为 Python 的环境和包管理工具，相比原生 Python 生态（如 pip 虚拟环境）有许多独特优势，尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处： 一、一站式环境管理&#xff1a…...

编程新知 2025/11/29 6:54:19

基于ASP.NET+ SQL Server实现（Web）医院信息管理系统

医院信息管理系统 1. 课程设计内容在 visual studio 2017 平台上，开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的综合运用 c#.net 知识，在 vs 2017 平台上，进行 ASP.NET 应用程序和简易网站的开发；初步熟悉开发一…...

编程新知 2025/12/14 0:24:50

基于服务器使用 apt 安装、配置 Nginx

🧾 一、查看可安装的 Nginx 版本首先，你可以运行以下命令查看可用版本： apt-cache madison nginx-core输出示例： nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

编程新知 2025/12/4 11:14:19

【Web 进阶篇】优雅的接口设计：统一响应、全局异常处理与参数校验

系列回顾： 在上一篇中，我们成功地为应用集成了数据库，并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了！但是，如果你仔细审视那些 API，会发现它们还很“粗糙”：有…...

编程新知 2025/11/25 4:57:19

ardupilot 开发环境eclipse 中import 缺少C++

目录文章目录目录摘要1.修复过程摘要本节主要解决ardupilot 开发环境eclipse 中import 缺少C++，无法导入ardupilot代码，会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

编程新知 2025/12/10 20:47:41

LeetCode - 199. 二叉树的右视图

题目 199. 二叉树的右视图 - 力扣（LeetCode） 思路右视图是指从树的右侧看，对于每一层，只能看到该层最右边的节点。实现思路是： 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

编程新知 2025/9/13 20:07:18

逻辑回归暴力训练预测金融欺诈

简述「使用逻辑回归暴力预测金融欺诈，并不断增加特征维度持续测试」的做法，体现了一种逐步建模与迭代验证的实验思路，在金融欺诈检测中非常有价值，本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

编程新知 2025/12/14 0:59:25

uniapp 实现腾讯云IM群文件上传下载功能

UniApp 集成腾讯云IM实现群文件上传下载功能全攻略一、功能背景与技术选型在团队协作场景中，群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS，在uniapp中实现： 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览二…...

编程新知 2025/9/14 20:44:53

6.9-QT模拟计算器

源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

编程新知 2025/12/7 8:17:50

[QMT量化交易小白入门]-六十二、ETF轮动中简单的评分算法如何获取历史年化收益32.7%

本专栏主要是介绍QMT的基础用法，常见函数，写策略的方法，也会分享一些量化交易的思路，大概会写100篇左右。 QMT的相关资料较少，在使用过程中不断的摸索，遇到了一些问题，记录下来和大家一起沟通，共同进步。文章目录相关阅读1. 策略概述2. 趋势评分模块3 代码解析4 木头…...

编程新知 2025/9/15 21:14:31

文章目录

💖 学习资源整合

📚 总复习

📙 选择题

📙 填空题

📙 大题

1. 概率

2. 概率

3. 概率

4. P

5. 概率

6. 概率密度函数 F ( X ) F(X) F(X)

7. 分布列求方差 V ( X ) V(X) V(X)

8. 求分布函数 F ( X ) F(X) F(X)

💖 速成课

一、事件的概率

1. 无放回类题目

2. 有放回类的题目

3. 需要画图的题目

4. 条件概率

5. 全概率公式

6. 贝叶斯公式

二、一维随机变量

1. F ( x ) 和 f ( x ) F(x) 和 f(x) F(x)和f(x) 知一求二

2. F ( x ) 和 f ( x ) F(x) 和 f(x) F(x)和f(x) 知一求 P P P

3. F ( x ) 和 f ( x ) F(x) 和 f(x) F(x)和f(x) 含未知数，求未知数

4. 求分布律

5. 已知含有未知数的分布列，求未知数

三、一维随机变量函数

1. 已知 X 分布列，求 Y 分布列

2. 已知 F X ( x ) F_X (x) FX​(x)，求 F Y ( y ) F_Y (y) FY​(y)

3. 已知 f X ( x ) f_X (x) fX​(x)，求 f Y ( y ) f_Y (y) fY​(y)

四、五种常见的分布

1. 均匀分布

2. 泊松分布

3. 二项分布

4. 指数分布

5. 正态分布

6. 正态分布图像

五、二维随机变量

1. 二维离散型分布律求概率

2. 二维离散型分布律求独立性

3. 知 F ( x , y ) F(x,y) F(x,y) 求 f ( x , y ) f(x,y) f(x,y)

4. 知 f ( x , y ) f(x,y) f(x,y) 求 F ( x , y ) F(x,y) F(x,y)

5. 已知 F ( x , y ) F(x,y) F(x,y) 求 P P P

6. 已知 f ( x , y ) f(x,y) f(x,y) 求 P P P

7. 已知 F ( x , y ) F(x,y) F(x,y) 或 f ( x , y ) f(x,y) f(x,y) 含有的未知数

8. 求均匀分布的 f ( x , y ) f(x,y) f(x,y) 与 P P P

六、期望与方差

1. 离散型的期望 E ( x ) E(x) E(x)

2. 连续型的期望 E ( X ) E(X) E(X)

3. Y = g ( x ) Y=g(x) Y=g(x) 求 E ( Y ) E(Y) E(Y)

4. 方差 D ( X ) D(X) D(X)

5. 根据 E ( X ) 、 D ( X ) E(X)、D(X) E(X)、D(X) 的性质进行复杂运算 ⭐

6. E ( X ) 、 D ( X ) E(X)、D(X) E(X)、D(X) 与各种分布的综合题 ⭐

七、中心极限定理

八、抽样分布

相关文章：

6. 概率密度函数 $F (X)$

7. 分布列求方差 $V (X)$

8. 求分布函数 $F (X)$

1. $F (x) 和 f (x)$ 知一求二

2. $F (x) 和 f (x)$ 知一求 $P$

3. $F (x) 和 f (x)$ 含未知数，求未知数

2. 已知 $F_X (x)$ ，求 $F_Y (y)$

3. 已知 $f_X (x)$ ，求 $f_Y (y)$

3. 知 $F (x, y)$ 求 $f (x, y)$

4. 知 $f (x, y)$ 求 $F (x, y)$

5. 已知 $F (x, y)$ 求 $P$

6. 已知 $f (x, y)$ 求 $P$

7. 已知 $F (x, y)$ 或 $f (x, y)$ 含有的未知数

8. 求均匀分布的 $f (x, y)$ 与 $P$

1. 离散型的期望 $E (x)$

2. 连续型的期望 $E (X)$

3. $Y = g (x)$ 求 $E (Y)$

4. 方差 $D (X)$

5. 根据 $E (X) 、 D (X)$ 的性质进行复杂运算 ⭐

6. $E (X) 、 D (X)$ 与各种分布的综合题 ⭐