信源编码与信道转移矩阵
目录
一. 信息论模型
二. 点对点通信模型
三. 信源编码
四. 信道转移矩阵
4.1 二进制对称信道
4.2 二进制擦除信道
五. 小结
(1)信道直射与反射
(2)信道散射
(3) 信道时变性
一. 信息论模型
1948年,Claude E. Shannon在《A mathematical theory of communication》论文中提出了信息论(information theory)。在点对点的通信中,发射方产生一个信息(比如像素的灰度值,传感器测量的物理量),接收方恢复出该信息。

信源(information source):根据随机性产生消息;
发射机(transmitter):产生信号;
信道(channel):包含噪声源,比如电路的热噪声,无线信道的多径衰落;
接收机(receiver):根据接受信号,恢复出消息;
一般提前已知信源与信道的统计特征,信息论尝试从数学的角度来解释安全传输流程。
二. 点对点通信模型
从模块化的角度来讲,物理层安全通信需要编码和解码的过程。信源编码的本质是压缩。
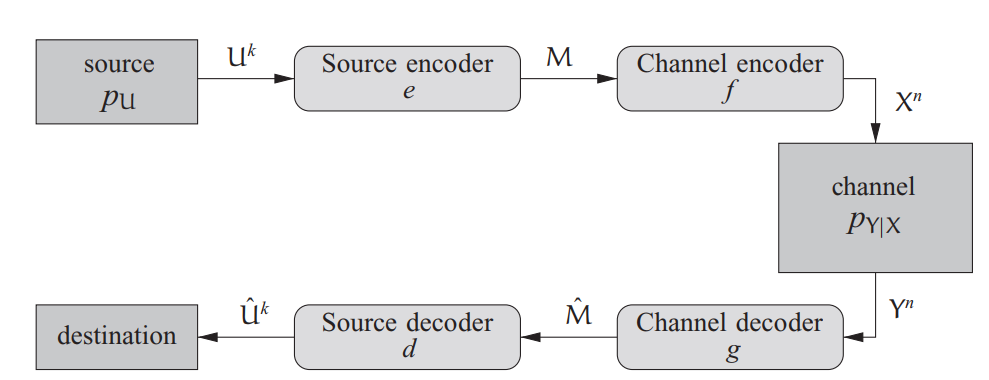
:信源符号;
M:消息;
:信道编码结果;
:信道传输结果;
:信道解码后的消息;
:解码后的信源符号;
三. 信源编码
信源是离散无记忆的DMS(discrete memoryless source),代表产生的符号都是独立同分布的,写做:
其中U代表有限字母集(alphabet),代表概率分布,也可以把U看做随机变量。
信源编码写做,其中k代表序列长度。编码后的消息集合为:
编码函数e可以将k长的信源符号编码成消息m,如下:
解码函数可以将一个消息m解码成k长的信源符号,当然也可能会出现解码失误,如下:
输入长度为k,输出长度为kR,所以压缩率为R。考虑一般性,kR可能非整数,所以压缩率(compression rate)的一般表达形式为:
单位为bit/source symbol。
当时,则会出现译码错误,由此可定义错误概率:
![]()
其中编码译码方案全局已知。在网络安全通信中,我们希望合法端错误概率低,窃听端错误概率高。
四. 信道转移矩阵
信道模型抽象成离散无记忆信道(discrete memoryless channel DMC),表示为:
其中X代表输入字母集,Y代表输出字母集,代表条件概率分布,也就是X代表信道输入,Y代表信道输出。
条件概率也可以写做信道转移矩阵,如下:
4.1 二进制对称信道
二进制对称信道,binary symmetric channel,BSC
BSC(P)也属于离散无记忆信道DMC,写做:
输入为0或1,输出为0或1。转移概率为P,代表0变1的概率为P,1变0的概率为P,0变0的概率为1-P,1变1的概率为1-P。写成信道转移矩阵,如下:

4.2 二进制擦除信道
二进制擦除信道,binary erasure channel, BEC
擦除概率写做,该信道模型为
,同样也属于离散无记忆信道DMC,如下:
0变成?的概率为,0变成0的概率为1-
,0变成1的概率为0
1变成?的概率为,1变成1的概率为1-
,1变成0的概率为0
写成信道转移矩阵如下:

五. 小结
无线信道具有互易性,时变性和空间唯一性。
典型无线信道环境中电磁波的基本传播机制如下图:
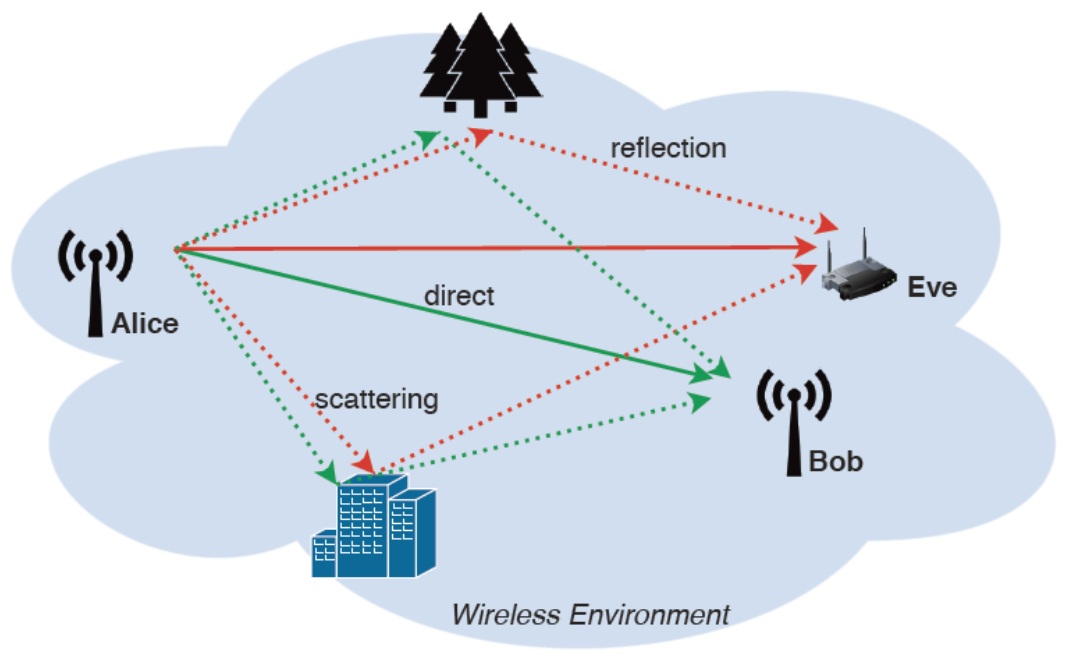
一般认为,无线通信中电波传播机制主要包括直射(direct)、反射(reflection)和散射(Scattering),有的场景还会涉及到折射、穿透等。
(1)信道直射与反射
直射传播指信号直接从发射天线到达接收天线,没有经过任何障碍物的传播方式。这种传播方式在空旷的地区效果最好,信号传输距离远,信噪比高。
反射传播指无线信号在遇到介质表面时,一部分能量被反射回去,沿原路返回,另一部分能量则继续传播的现象。这种传播方式通常发生在金属、水面、建筑物等表面。
反射信号与直射信号叠加在一起,形成多路径传播的效应。
(2)信道散射
散射传播指信号在经过物体表面或介质中微小不规则的颗粒或边缘时,发生多次反射、折射、绕射等现象,使得信号在空间中分散的传播方式。这种传播方式会造成信号的强度分布不均匀,信号失真和多径效应等问题。
另外,存在直射传播的信道被称为视距传输(Line-of-Sight, LOS),而其他传播机制的信道被称为非视距传输(Non-line of Sight, NLOS)。
(3) 信道时变性
无线信道衰落可以分为大尺度衰落和小尺度衰落,又称为快衰落和慢衰落。大尺度衰落是指在信号传输的大范围距离内(一般为数百米以上),由于信号的路径损耗和阴影衰落等因素导致的信号功率变化。大尺度衰落的特点是空间相关性强,变化缓慢,可以通过减小传输距离、使用更高的天线高度、增大发送功率等方法来降低其影响。
小尺度衰落是指在信号传输的短距离范围内(一般为数十米以下),由于信号经历多条不同路径导致的信号幅度和相位的随机变化,包括多径效应和多普勒效应等。小尺度衰落的特点是空间相关性弱,变化快速,可以通过使用合适的调制技术、信号预处理、天线阵列等方法来抑制或利用其特性来提高系统性能。
小尺度衰落,时域上对应多径效应, 频率域上对应多普勒频移效应引发的频率色散。若考虑多输入多输出 MIMO技术,小尺度衰落还需要考虑空域上的特性,即无线信道的空间角度扩展信息。
总的来说,大尺度衰落主要受到距离和环境的影响,而小尺度衰落主要受到多径效应和信号随机性的影响。
相关文章:

信源编码与信道转移矩阵
目录 一. 信息论模型 二. 点对点通信模型 三. 信源编码 四. 信道转移矩阵 4.1 二进制对称信道 4.2 二进制擦除信道 五. 小结 (1)信道直射与反射 (2)信道散射 (3) 信道时变性 一. 信息论模型 194…...

React 实现拖放功能
介绍 本篇文章将会使用react实现简单拖放功能。 样例 布局侧边栏拖放 LayoutResize.js import React, {useState} from "react"; import { Button } from "antd"; import "./LayoutResize.css";export const LayoutResize () > {const […...

马克思主义基本原理笔记
马克思主义哲学、政治经济学、科学社会主义理论 哲学 马克思主义中国化的理论成果:毛泽东思想、邓小平理论、三个代表重要思想、科学发展观 物质和意识哪个是本原,是哲学的基本问题 辩证法认为世界上的事物都是相互联系的、运动发展的,形…...
)
Vue+JavaSpingBoot笔记(1)
一、前后端通信参数问题 1.集合【字典】类型 Vue前端传递参数: export default {methods: { test(){// 将 filteredData 中的每一行值放入 newData 对象数组中 const newData filteredData.map(item > ({key1: item.Value1,key2: item.Value2,key3: "测试"}));r…...
)
10-单例模式(Singleton)
意图 保证一个类只有一个实例,并提供一个访问它的全局访问点 实现 1 懒汉式,线程不安全 public class Singleton { private static Singleton instance; private Singleton (){} public static Singleton getInstance() { if (instance null) {…...

C++ 求一个数是否是丑数。
#include<string.h> #include <iostream> using namespace std; int isChou(int num) { if (num < 0) { return 0; } while (num % 2 0) { // 不断除以2,直到不能整除为止 num / 2; } while (num % 3 0) { // 不断除…...
SpringCloud系列篇:核心组件之注册中心组件
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于SpringCloud的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.注册中心组件是什么 二.注册中心…...

通过IP地址防范钓鱼网站诈骗的有效措施
随着互联网的普及,钓鱼网站诈骗成为一种广泛存在的网络犯罪行为。通过冒充合法网站,攻击者试图窃取用户的敏感信息。本文将探讨如何通过IP地址防范钓鱼网站诈骗,提供一系列有效的措施,以加强网络安全,保护用户免受诈骗…...

服务器GPU温度过高挂掉排查记录
服务器GPU挂掉 跑深度学习的代码的时候发现中断了。通过命令查看: nvidia-smi显示 Unable to determine the device handle for GPU 0000:01:00.0: Unknown Error。感觉很莫名其妙。通过重启大法之后,又能用一段时间。 shutdown -r now但是过了一个小…...
服务器终端快速下载coco数据集
######解压到当前文件夹 sudo apt-get install aria2 aria2c -c <url> #<url>即为官网下载地址# url # download images http://images.cocodataset.org/zips/train2017.zip http://images.cocodataset.org/zips/val2017.zip# download annotations http://i…...
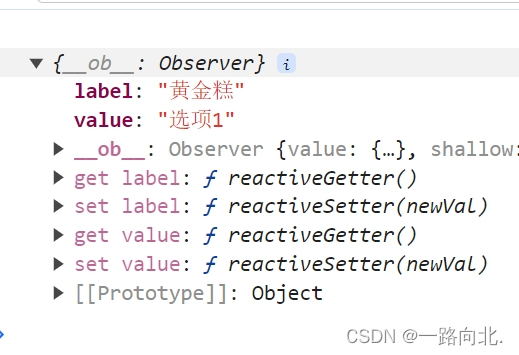
el-select下拉框 change事件返回该项所有数据
主要代码 value-key <template><div><el-selectv-model"value"value-key"label"placeholder"请选择"change"selectChange"><el-optionv-for"item in options":key"item.label":label"…...
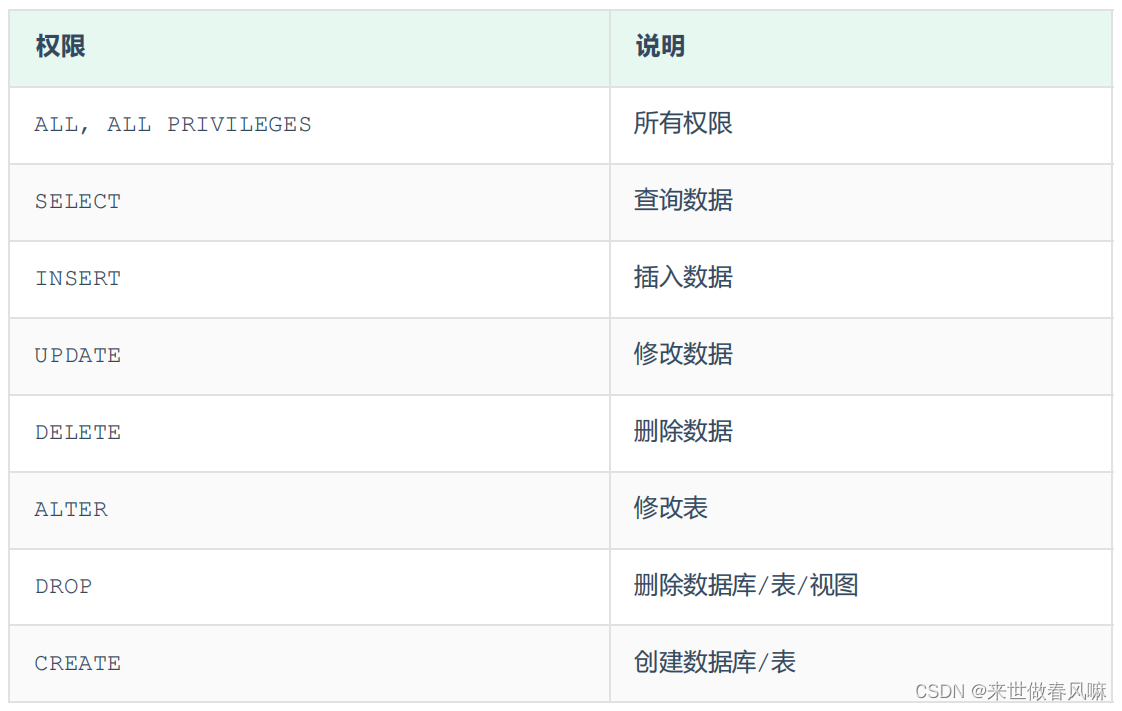
MySQL基础篇(一)SQL
视频地址: 黑马程序员 MySQL数据库入门到精通,从mysql安装到mysql高级、mysql优化全囊括 SQL,全称 Structured Query Language,结构化查询语言。操作关系型数据库的编程语言,定义了一套操作关系型数据库统一 标准。 一、SQL通用语…...

多类指针式仪表自动读数系统的LabVIEW开发应用案例
多类指针式仪表自动读数系统的LabVIEW开发应用案例 工业环境中,多类指针式仪表的自动读数一直是一个具有挑战性的问题。本案例旨在展示如何使用LabVIEW开发一个高度智能化的多类指针式仪表自动读数系统,以应对复杂的工业环境。通过结合图像处理技术和深…...
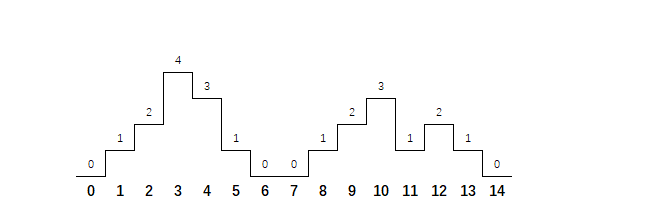
攀登者2 - 华为OD统一考试
OD统一考试 分值: 200分 题解: Java / Python / C++ 题目描述 攀登者喜欢寻找各种地图,并且尝试攀登到最高的山峰。 地图表示为一维数组,数组的索引代表水平位置,数组的元素代表相对海拔高度。其中数组元素0代表地面。 例如:[0,1,2,4,3,1,0,0,1,2,3,1,2,1,0],代表如下…...

归并排序例题——逆序对的数量
做道简单一点的题巩固一下 归并排序实现步骤 将整个区间 [l, r] 划分为 [l, mid] 和 [mid1, r]。 递归排序 [l, mid] 和 [mid1, r]。 将左右两个有序序列合并为一个有序序列。 题目描述 给定一个长度为 n 的整数数列,请计算数列中的逆序对的数量。 逆序对的定义…...

数据库连接使用问题 - 1
原理 open-in-view 是 Spring Boot ⾃动加载 Spring Data JPA 提供的⼀个配置,全称为 spring.jpa.open-in-viewtrue,它只有 true 和 false 两个值,默认是 true。 这个配置为true时,会导致Web MVC请求处理的一开始&…...

【已解决】You have an error in your SQL syntax
报错讯息 java.sql.SQLSyntaxErrorException: You have an error in your SQL syntax; check the manual that corresponds to your MySQL server version for the right syntax to use near ‘desc,target_url,sort,status,create_by,modify_by,created,last_update_time FROM…...
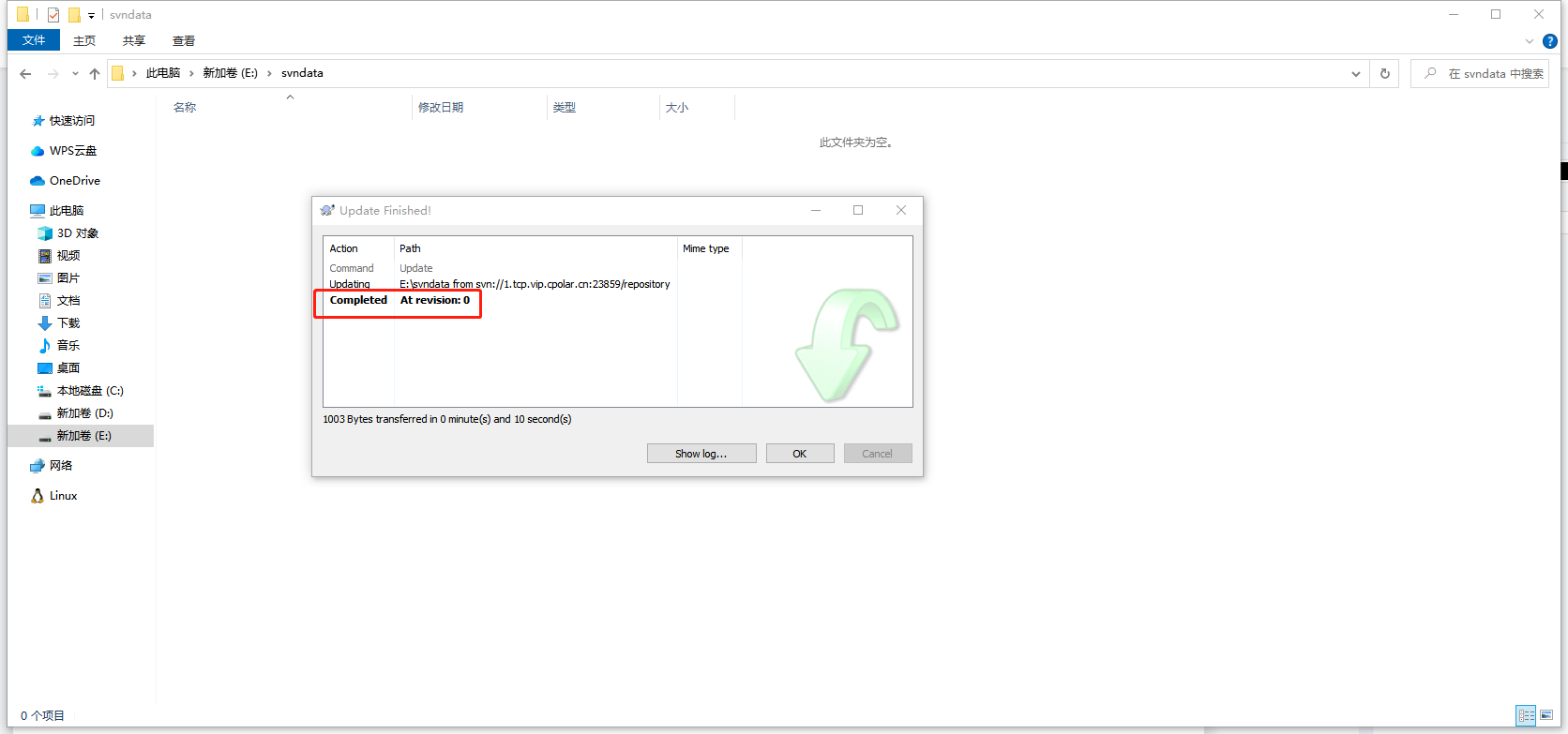
如何在Ubuntu安装SVN服务并结合cpolar实现公网TCP地址远程访问本地服务
文章目录 前言1. Ubuntu安装SVN服务2. 修改配置文件2.1 修改svnserve.conf文件2.2 修改passwd文件2.3 修改authz文件 3. 启动svn服务4. 内网穿透4.1 安装cpolar内网穿透4.2 创建隧道映射本地端口 5. 测试公网访问6. 配置固定公网TCP端口地址6.1 保留一个固定的公网TCP端口地址6…...

windows监控进程是否还活着,查看内存使用率
windows监控进程是否还活着,查看内存使用率 1、导入库psutil pip install psutil2、查看进程是否活着 def is_process_running(self, process_name):# 查看程序是否还存活for process in psutil.process_iter():try:if process.name() process_name:return True…...

C#-词法结构
程序 C# 程序 (program) 由一个或多个源文件 (source file) 组成,源文件的正式名称是编译单元 (compilation unit)。源文件是有序的 Unicode 字符序列。 源文件与文件系统中的文件通常具有一对一的对应关系,但这种对应关系不是必需的。为实现可移植性的最大化,建议这些文件…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
