线性代数 --- 为什么LU分解中L矩阵的行列式一定等于正负1?
以下是关于下三角矩阵L的行列式一定等于+-1的一些说明
笔者的一些话(写在最前面):
这是一篇小文,是我写的关于求解矩阵行列式的一篇文章中的一部分。之所以把这一段专门提溜出来,是因为这一段相对于原文是可以完全独立的,也是因为我自认为这是原文中很精彩的一段论证。为了便于我自己后续翻阅和查找,也是为了给我CSDN文章里面凑数,这才有了这篇文章。
证明:在LU分解中,下三角矩阵L的行列式一定是.
在证明之前,我这里先补充几条关于行列式的性质:
性质1:对于三角矩阵而言,不论是上三角矩阵还是下三角矩阵,其行列式的值都等于主对角线上元素的乘积。

此处引用Gilbert strang的线性代数教科书《introduction to linear algebra》中,第251页处的一段关于矩阵行列式的相应说明:

截图中第七条性质说:如果矩阵A是一个三角矩阵,则矩阵A的行列式等于其对角线上元素的乘积。
性质2:两个矩阵A,B的积AB的行列式|AB|等于这两个矩阵各自的行列式|A|和|B|的积,即:

性质3:单位矩阵I的行列式为1。
性质4:对矩阵进行行与行之间的交换后,需要改变原矩阵行列式的正负号。

在LU分解中,下三角阵L是高斯消元的逆过程,是多个消元矩阵E的逆矩阵的乘积(形如下图中的矩阵)。

首先,根据上面说的性质1可知,所有消元矩阵E的逆矩阵的行列式等于其对角线上所有元素的乘积。又因为矩阵
对角线上元素都是1,所以,
的行列式一定等于1。此外,根据性质2,L的行列式等于多个
的行列的乘积,所以,L的行列式必然等于1,即:
可是,如果对矩阵A进行高斯消元的过程中,遇到对角线上的元素为0的情况,就需要对矩阵进行行交换,则上式就会包含一些置换矩阵:
这种情况下计算出来的L矩阵可就不一定是标准的下三角矩阵了,比如说下面这个矩阵:

这样一来就需要对L矩阵进行行交换,把他变成标准的下三角矩阵,以确保他的det等于1。而交换的过程需要用置换矩阵P记录下来,使得原来的L,变成PL(这时的L已经是标准的下三角矩阵了)。因为置换矩阵P只不过是对单位矩阵I进行行交换后的结果,因此,综合性质3和性质4可知,置换矩阵P的行列式的值只能是+1或-1。在结合前面得出的L矩阵的行列式一定是1的结论,最终PL的行列式只能是+1或-1。
因此,当我们基于矩阵A的LU分解计算出L的det后(必然是1),如果高斯消元的过程中进行过行交换,还要再根据行交换的次数(置换矩阵P)去调整det的符号。
事实上,在matlab中自带的计算矩阵行列式的det函数就利用了这一点。
按照Matlab的官方说明文档,首先,他在计算矩阵的det时先调了lu分解函数,对矩阵进行分解。
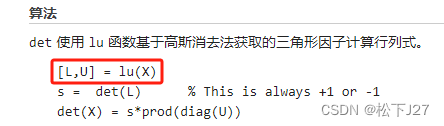
注意,matlab的lu分解函数有很多,只是他在计算行列式时,调用的是[L,U]=lu(A)。
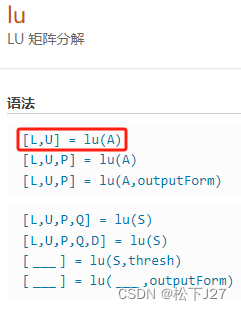
 按照他官方文档的说法,分解后的L矩阵和U矩阵中,L矩阵有被置换过,也就不是标准的三角矩阵。这和我们前面提到的,如果消元时进行过行交换的情况是一致的。
按照他官方文档的说法,分解后的L矩阵和U矩阵中,L矩阵有被置换过,也就不是标准的三角矩阵。这和我们前面提到的,如果消元时进行过行交换的情况是一致的。
然后,对这个“经过置换的下三角矩阵L”进行行交换,并记录交换过程得到:
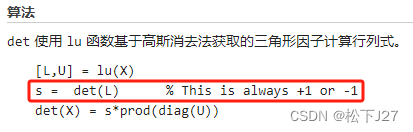
最后一步,求出矩阵U(他一定是一个标准的上三角矩阵)中主对角线上所有元素的乘积,然后和前一步的结果相乘,得到矩阵A的行列式:
例子:


(全文完)
作者 --- 松下J27
参考文献(鸣谢):
1,https://en.wikipedia.org/wiki/Determinant
2,Determinant of a Matrix
3,矩阵行列式 - MATLAB det- MathWorks 中国
4,线性代数 --- LU分解(Gauss消元法的矩阵表示)_矩阵的lu分解-CSDN博客
5,线性代数 --- Gauss消元的部分主元法和完全主元法_部分选主元高斯matlab-CSDN博客

(配图与本文无关)
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27
相关文章:

线性代数 --- 为什么LU分解中L矩阵的行列式一定等于正负1?
以下是关于下三角矩阵L的行列式一定等于-1的一些说明 笔者的一些话(写在最前面): 这是一篇小文,是我写的关于求解矩阵行列式的一篇文章中的一部分。之所以把这一段专门提溜出来,是因为这一段相对于原文是可以完全独立的,也是因为我…...
Redisson 源码解析 - 分布式锁实现过程
一、Redisson 分布式锁源码解析 Redisson是架设在Redis基础上的一个Java驻内存数据网格。在基于NIO的Netty框架上,充分的利用了Redis键值数据库提供的一系列优势,在Java实用工具包中常用接口的基础上,为使用者提供了一系列具有分布式特性的常…...
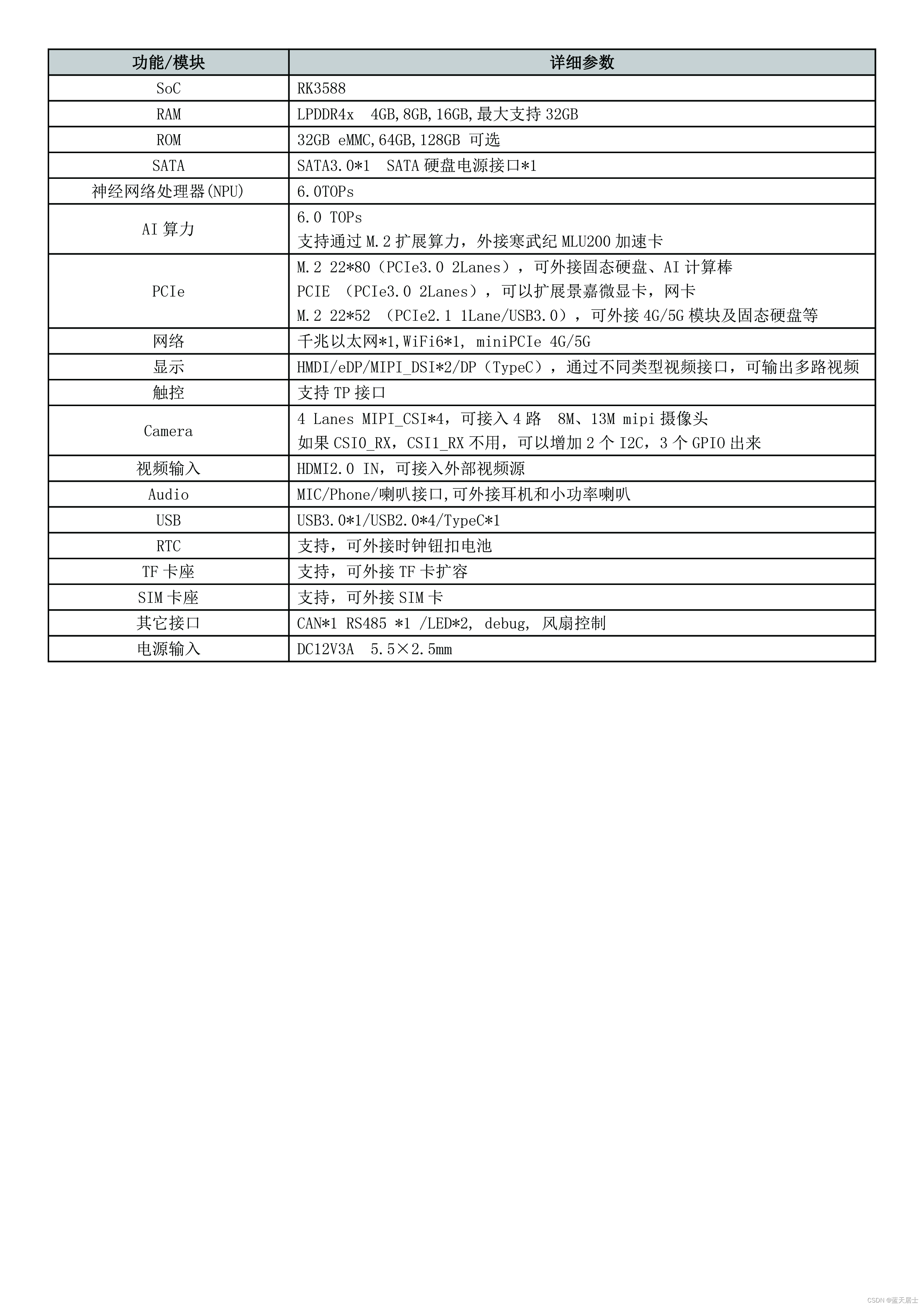
玩转贝启科技BQ3588C开源鸿蒙系统开发板 —— 开发板详情与规格
本文主要参考: BQ3588C_开发板详情-开源鸿蒙技术交流-Bearkey-开源社区 BQ3588C_开发板规格-开源鸿蒙技术交流-Bearkey-开源社区 厦门贝启科技有限公司-Bearkey-官网 1. 开发板详情 RK3588 核心板是一款由贝启科技自主研发的基于瑞芯微 RK3588 AI 芯片的智能核心…...
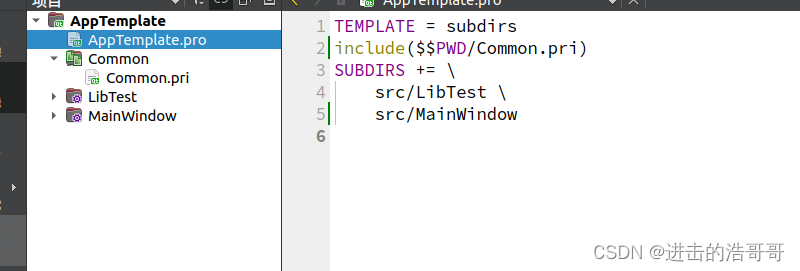
Qt pro文件
1. 项目通常结构 2.pri文件 pri文件可定义通用的宏,例如创建一个COMMON.pri文件内容为 COMMON_PATH D:\MyData 然后其它pri或者pro文件如APPTemplate.pro文件中通过添加include(Common.pri) ,QtCreator就会自动在项目结构树里面创建对应的节点 3.变量…...
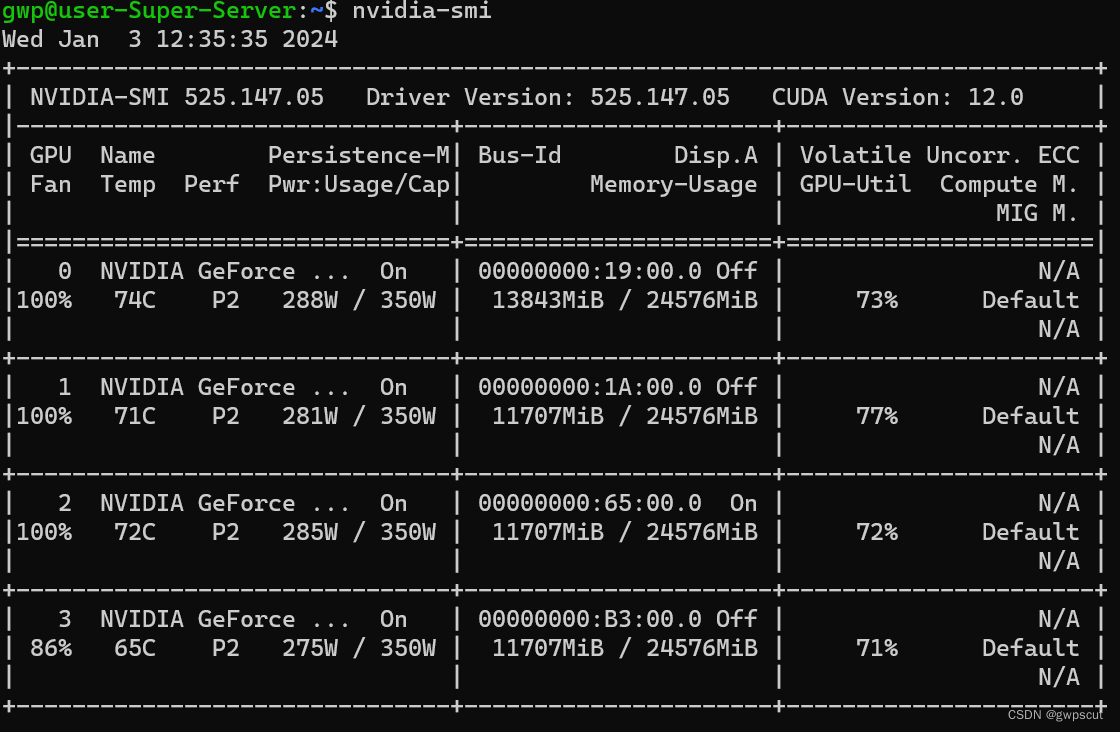
实验笔记之——服务器链接
最近需要做NeRF相关的开发,需要用到GPU,本博文记录本人配置服务器远程链接的过程,本博文仅供本人学习记录用~ 连上服务器 首先先确保环境是HKU的网络环境(HKU AnyConnect也可)。伙伴已经帮忙创建好用户(第一次登录会提示重新设置密码)。用cmd ssh链接ssh -p 60001 <u…...
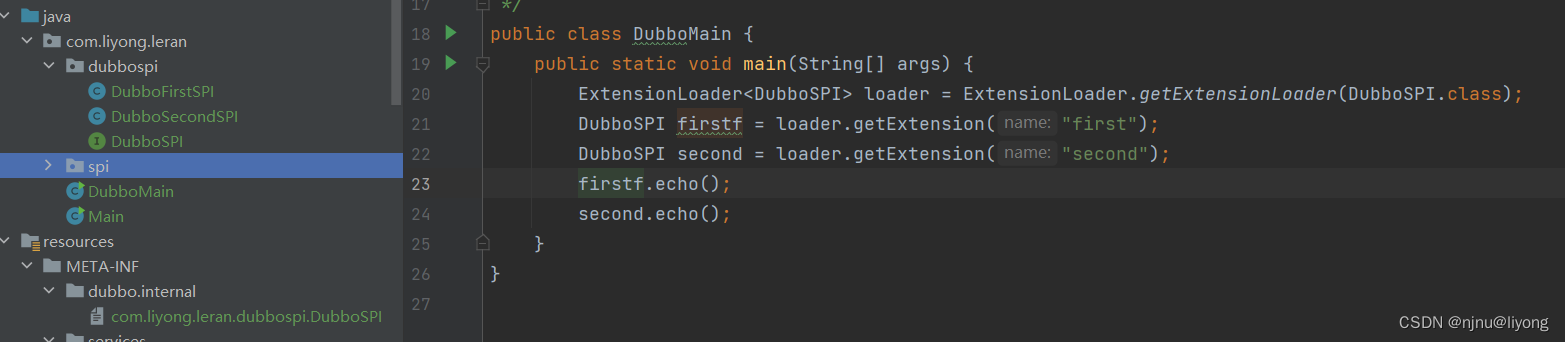
微服务-java spi 与 dubbo spi
Java SPI 通过一个案例来看SPI public interface DemoSPI {void echo(); } public class FirstImpl implements DemoSPI{Overridepublic void echo() {System.out.println("first echo");} } public class SecondImpl implements DemoSPI{Overridepublic void ech…...

redis复习笔记03(小滴课堂)
Redis6常见数据结构概览 0代表存在,1代表不存在。 1表示删除成功,0表示失败。 查看类型,默认string类型。 也可以设置set类型。 list类型。 查看key的过期时间: Redis6数据结构之String类型介绍和应用场景 批量设置: …...
【Spring Cloud】关于Nacos配置管理的详解介绍
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《Spring Cloud》。🎯🎯 &am…...
基于Java SSM框架实现校园网络维修系统项目【项目源码】
基于java的SSM框架实现校园网络维修系统演示 java简介 Java主要采用CORBA技术和安全模型,可以在互联网应用的数据保护。它还提供了对EJB(Enterprise JavaBeans)的全面支持,java servlet API,JSP(java serve…...
项目框架构建之3:Nuget服务器的搭建
本文是“项目框架构建”系列之3,本文介绍一下Nuget服务器的搭建,这是一项简单的工作,您或许早已会了。 1.打开vs2022创建Asp.net Web应用程序 框架选择.net framework4.8,因为nuget服务器只支持.net framework。 2.选择空项目和保…...
外包干了1个月,技术退步一大半。。。
先说一下自己的情况,本科生,19年通过校招进入广州某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
)
167. 木棒(dfs剪枝,经典题)
167. 木棒 - AcWing题库 乔治拿来一组等长的木棒,将它们随机地砍断,使得每一节木棍的长度都不超过 50 个长度单位。 然后他又想把这些木棍恢复到为裁截前的状态,但忘记了初始时有多少木棒以及木棒的初始长度。 请你设计一个程序࿰…...

用HTML的原生语法实现两个div子元素在同一行中排列
代码如下: <div id"level1" style"display: flex;"><div id"level2-1" style"display: inline-block; padding: 10px; border: 1px solid #ccc; margin: 5px;">这是第一个元素。</div><div id"…...
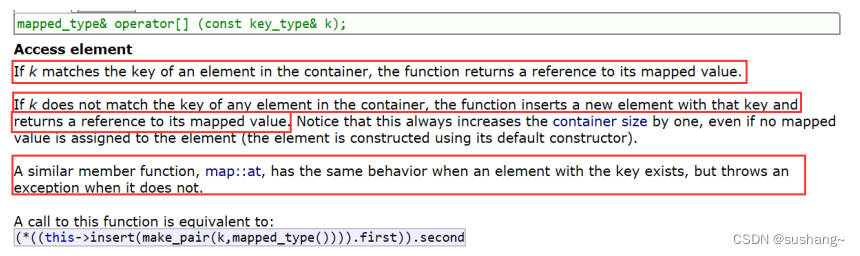
C++进阶--map和set的介绍及使用
map和set的介绍及使用 一、关联式容器与键值对关联式容器键值对pair树形结构的关联式容器 二、set2.1 set的介绍2.2 set的使用2.2.1 set的模板参数列表2.2.2 set的构造2.2.3 set的迭代器2.2.4 set的容量2.2.5 set修改操作2.2.6 set的使用举例 三、multiset3.1 multiset的介绍3.…...
MIML-DA
图3呢?且作者未提供代码...
[ROS2 Foxy]#1.3 安装使用 turtlesim
官网教程: https://docs.ros.org/en/foxy/Tutorials/Turtlesim/Introducing-Turtlesim.html 1.turtlesim安装和使用 turtlesim是一个轻量级的模拟程序,用来学习ROS2 .通过turtlesim来介绍ROS2在一个基础的水平上都要做了那些事,以此让我们了解将来在真的 robot或者模拟器上使用…...

嵌入式培训机构四个月实训课程笔记(完整版)-Linux系统编程第三天-Linux进程(物联技术666)
更多配套资料CSDN地址:点赞+关注,功德无量。更多配套资料,欢迎私信。 物联技术666_嵌入式C语言开发,嵌入式硬件,嵌入式培训笔记-CSDN博客物联技术666擅长嵌入式C语言开发,嵌入式硬件,嵌入式培训笔记,等方面的知识,物联技术666关注机器学习,arm开发,物联网,嵌入式硬件,单片机…...
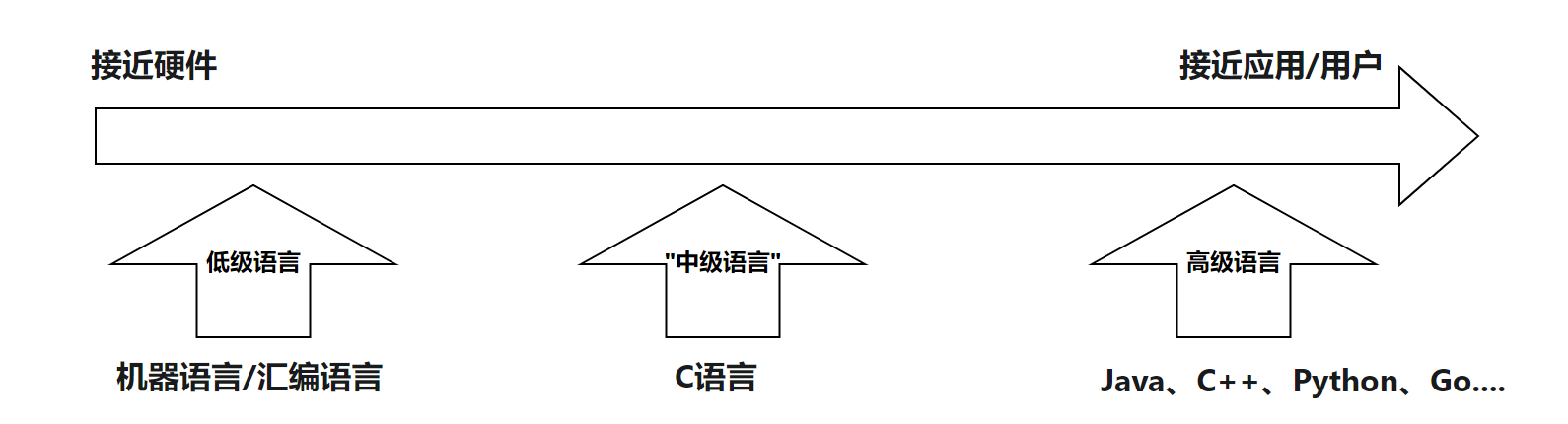
1-01初识C语言
一、概述 C语言是贝尔实验室的Ken Thompson(肯汤普逊)、Dennis Ritchie(丹尼斯里奇)等人开发的UNIX 操作系统的“副产品”,诞生于1970年代初。 Thompson和Ritchie共同创作完成了Unix操作系统,他们都被称为…...

Python字符串
定义字符串 Python中要定义一个字符串,有比较多的一种方式。 示例代码: s "你好,张大鹏" print(s, type(s))s 你好,张大鹏 print(s, type(s))s """你好,张大鹏""" prin…...
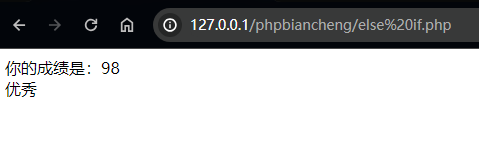
PHP 基础编程 1
文章目录 前后端交互尝试php简介php版本php 基础语法php的变量前后端交互 - 计算器体验php数据类型php的常量和变量的区别php的运算符算数运算符自增自减比较运算符赋值运算符逻辑运算 php的控制结构ifelseelse if 前后端交互尝试 前端编程语言:JS (Java…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

使用ch340继电器完成随机断电测试
前言 如图所示是市面上常见的OTA压测继电器,通过ch340串口模块完成对继电器的分路控制,这里我编写了一个脚本方便对4路继电器的控制,可以设置开启时间,关闭时间,复位等功能 软件界面 在设备管理器查看串口号后&…...
