167. 木棒(dfs剪枝,经典题)
167. 木棒 - AcWing题库
乔治拿来一组等长的木棒,将它们随机地砍断,使得每一节木棍的长度都不超过 50 个长度单位。
然后他又想把这些木棍恢复到为裁截前的状态,但忘记了初始时有多少木棒以及木棒的初始长度。
请你设计一个程序,帮助乔治计算木棒的可能最小长度。
每一节木棍的长度都用大于零的整数表示。
输入格式
输入包含多组数据,每组数据包括两行。
第一行是一个不超过 64 的整数,表示砍断之后共有多少节木棍。
第二行是截断以后,所得到的各节木棍的长度。
在最后一组数据之后,是一个零。
输出格式
为每组数据,分别输出原始木棒的可能最小长度,每组数据占一行。
数据范围
数据保证每一节木棍的长度均不大于 50。
输入样例:
9
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0
输出样例:
6
5解析:
本题是一道经典的dfs剪枝题,主要有三种剪枝:
剪枝 1:sum % length == 0 只有 length是 sum的约数才有可能凑出多个等长的木棒
剪枝 2:优化搜索顺序,木棍长度从大到小排序,可以减少搜索的分支
排除等效冗余优化:
剪枝 3-1:确定每根木棒中木棍的枚举顺序,因为我们的方案和顺序没有关系,以组合的形 式枚举方案可以少搜很多重复方案
剪枝 3-2:如果当前木棍没有搜到方案,则跳过所有长度相等的木棍
剪枝 3-3:如果是木棒的第一根木棍就搜索失败了,则一定搜不到方案
剪枝 3-4:如果是木棒的最后一根木棍(+ 上它木棒长度正好是 length)搜索失败了,也一 定搜不到方案
可以想想怎么证明上述几种剪枝的正确性,dfs和动态规划很像
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
using namespace std;
const int N = 70;
int n;
int ar[N],vis[N], len, sum;int cmp(const int& a, const int& b) {return a > b;
}bool dfs(int u, int s,int start) {/*cout << "KKKKKKKKKKKKKKKKK "<<len<<" "<<s << endl;for (int i = 1; i <= n; i++) {cout << vis[i] << " ";}cout << endl << endl;*/if (u * len == sum) {/*cout << "_______________" << u << endl;*/return 1;}if (s == len) {return dfs(u + 1, 0, 0);/*if (dfs(u + 1, 0, 0)) {cout << "LLLLLLLLLLLLL " << 1 << endl;return 1;}*/}for (int i = start; i <= n; i++) {if (vis[i])continue;if (s + ar[i] > len)continue;vis[i] = 1;if (dfs(u, s + ar[i], i + 1))return 1;vis[i] = 0;if (s == 0 || s + ar[i] == len)return 0;int j = i;while (j <= n && ar[j] == ar[i])j++;i = j - 1;}return 0;
}int main() {while (cin >> n, n) {int mx = 0;sum = 0;for (int i = 1; i <= n; i++) {scanf("%d", &ar[i]);sum += ar[i];mx = max(mx, ar[i]);}memset(vis, 0, sizeof vis);sort(ar + 1, ar + 1 + n, cmp);len = mx;while (1) {while (sum % len != 0)len++;//cout << "++++++"<<len << endl;if (dfs(0, 0, 1)) {printf("%d\n", len);break;}len++;}}return 0;
}
相关文章:
)
167. 木棒(dfs剪枝,经典题)
167. 木棒 - AcWing题库 乔治拿来一组等长的木棒,将它们随机地砍断,使得每一节木棍的长度都不超过 50 个长度单位。 然后他又想把这些木棍恢复到为裁截前的状态,但忘记了初始时有多少木棒以及木棒的初始长度。 请你设计一个程序࿰…...

用HTML的原生语法实现两个div子元素在同一行中排列
代码如下: <div id"level1" style"display: flex;"><div id"level2-1" style"display: inline-block; padding: 10px; border: 1px solid #ccc; margin: 5px;">这是第一个元素。</div><div id"…...
C++进阶--map和set的介绍及使用
map和set的介绍及使用 一、关联式容器与键值对关联式容器键值对pair树形结构的关联式容器 二、set2.1 set的介绍2.2 set的使用2.2.1 set的模板参数列表2.2.2 set的构造2.2.3 set的迭代器2.2.4 set的容量2.2.5 set修改操作2.2.6 set的使用举例 三、multiset3.1 multiset的介绍3.…...
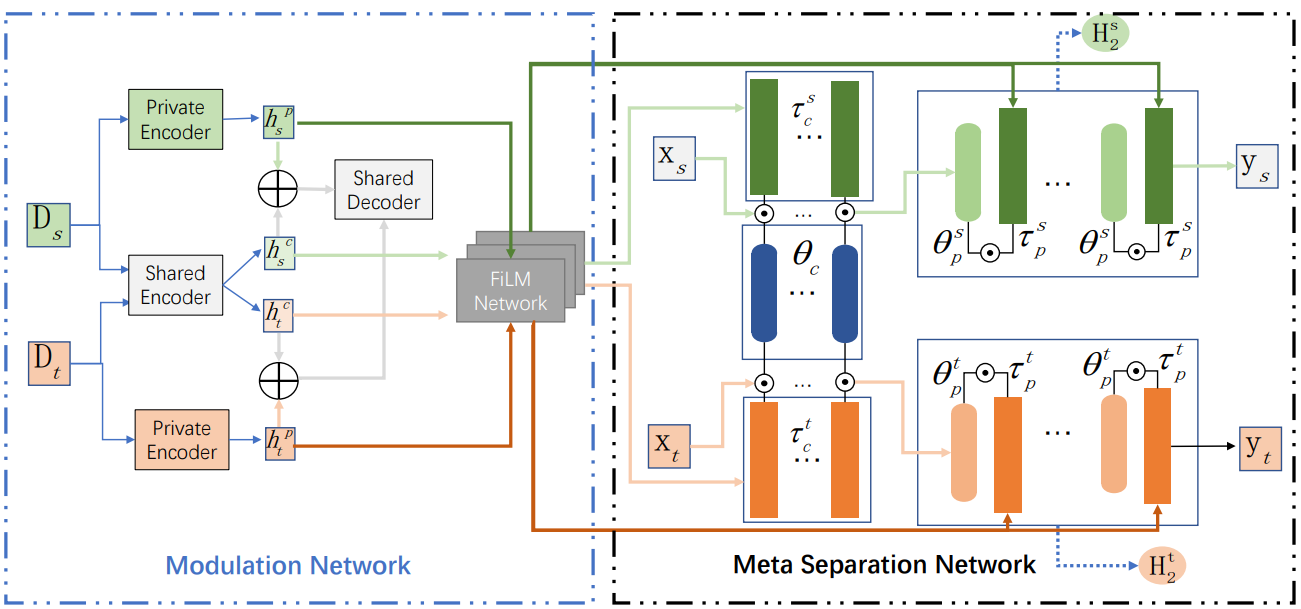
MIML-DA
图3呢?且作者未提供代码...
[ROS2 Foxy]#1.3 安装使用 turtlesim
官网教程: https://docs.ros.org/en/foxy/Tutorials/Turtlesim/Introducing-Turtlesim.html 1.turtlesim安装和使用 turtlesim是一个轻量级的模拟程序,用来学习ROS2 .通过turtlesim来介绍ROS2在一个基础的水平上都要做了那些事,以此让我们了解将来在真的 robot或者模拟器上使用…...

嵌入式培训机构四个月实训课程笔记(完整版)-Linux系统编程第三天-Linux进程(物联技术666)
更多配套资料CSDN地址:点赞+关注,功德无量。更多配套资料,欢迎私信。 物联技术666_嵌入式C语言开发,嵌入式硬件,嵌入式培训笔记-CSDN博客物联技术666擅长嵌入式C语言开发,嵌入式硬件,嵌入式培训笔记,等方面的知识,物联技术666关注机器学习,arm开发,物联网,嵌入式硬件,单片机…...
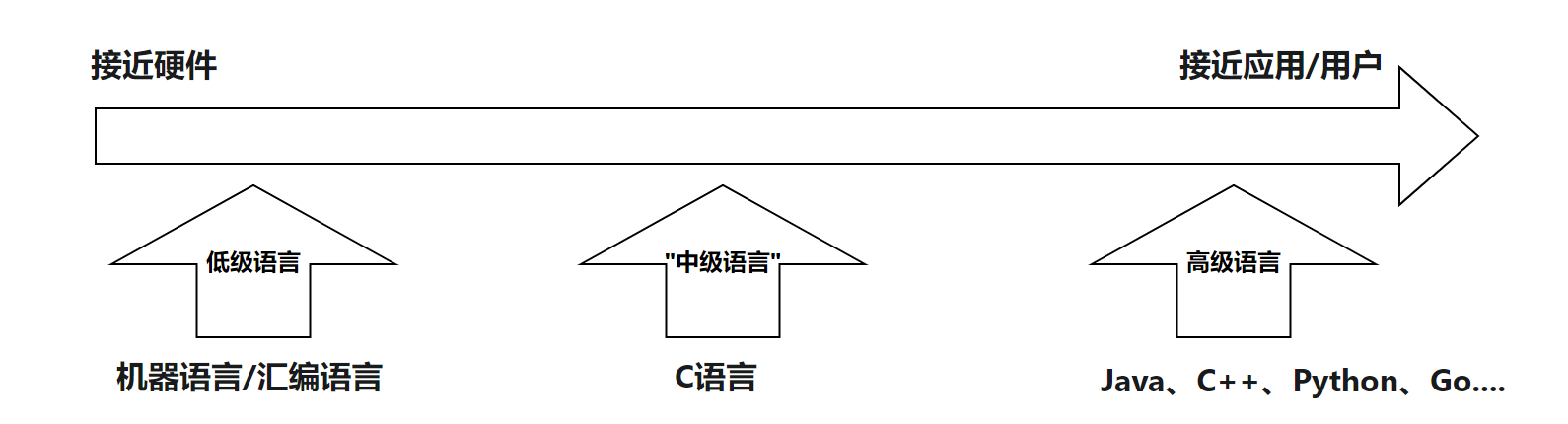
1-01初识C语言
一、概述 C语言是贝尔实验室的Ken Thompson(肯汤普逊)、Dennis Ritchie(丹尼斯里奇)等人开发的UNIX 操作系统的“副产品”,诞生于1970年代初。 Thompson和Ritchie共同创作完成了Unix操作系统,他们都被称为…...

Python字符串
定义字符串 Python中要定义一个字符串,有比较多的一种方式。 示例代码: s "你好,张大鹏" print(s, type(s))s 你好,张大鹏 print(s, type(s))s """你好,张大鹏""" prin…...
PHP 基础编程 1
文章目录 前后端交互尝试php简介php版本php 基础语法php的变量前后端交互 - 计算器体验php数据类型php的常量和变量的区别php的运算符算数运算符自增自减比较运算符赋值运算符逻辑运算 php的控制结构ifelseelse if 前后端交互尝试 前端编程语言:JS (Java…...

Android studio BottomNavigationView 应用设计
一、新建Bottom Navigation Activity项目: 二、修改bottom_nav_menu.xml: <itemandroid:id="@+id/navigation_beijing"android:icon="@drawable/ic_beijing_24dp"android:title="@string/title_beijing" /><itemandroid:id="@+i…...

51单片机串行口相关知识
51单片机串行口相关知识 串行通信概念 计算机与外部通信方式就两种: 并行通信串行通信 两种通信方式的特点以及适用场景: 名称特点适用场景并行通信速度快,效率高,成本高适合短距离高速通信,如计算机内部各硬件之…...
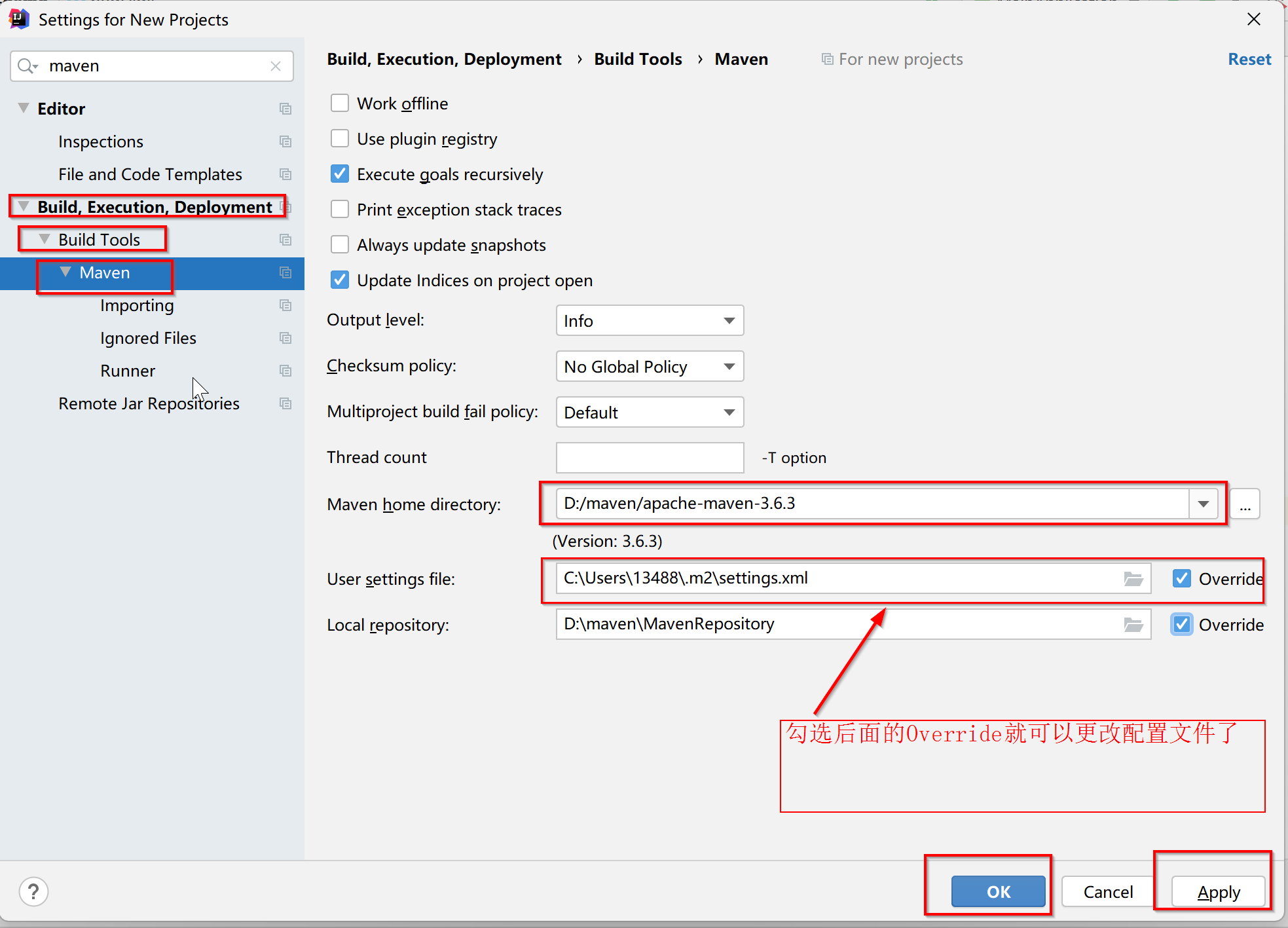
IDEA 每次新建工程都要重新配置 Maven的解决方案
文章目录 IDEA 每次新建工程都要重新配置 Maven 解决方案一、选择 File -> New Projects Setup -> Settingsfor New Projects…二、选择 Build,Execution,Deployment -> Build Tools -> Maven IDEA 每次新建工程都要重新配置 Maven 解决方案 DEA 每次新建工程都要…...
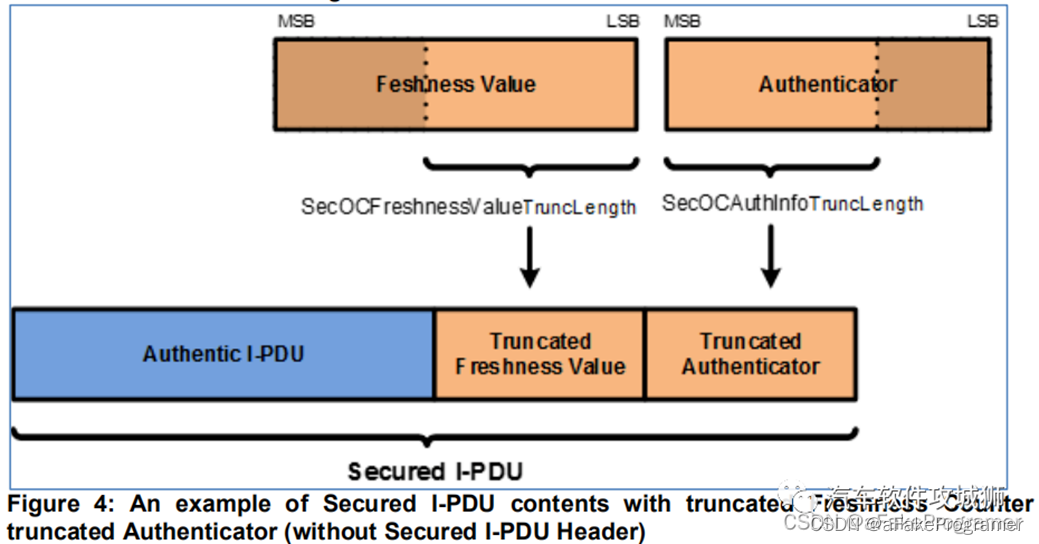
SecOC中新鲜度值和MAC都按照完整的值来生成,但是在发送和认证的时候只会截取一部分。这边截取的部分一般取多长?由什么参数设定?
新鲜度值(Freshness Value, FV)和消息验证码(Message Authentication Code, MAC)是SecOC协议中用于保证数据的真实性和新鲜度的重要信息。它们的长度取决于不同的因素,如加密算法、安全级别、通信带宽等。 一般来说,FV和MAC的长度越长,安全性越高,但也会占用更多的通信…...
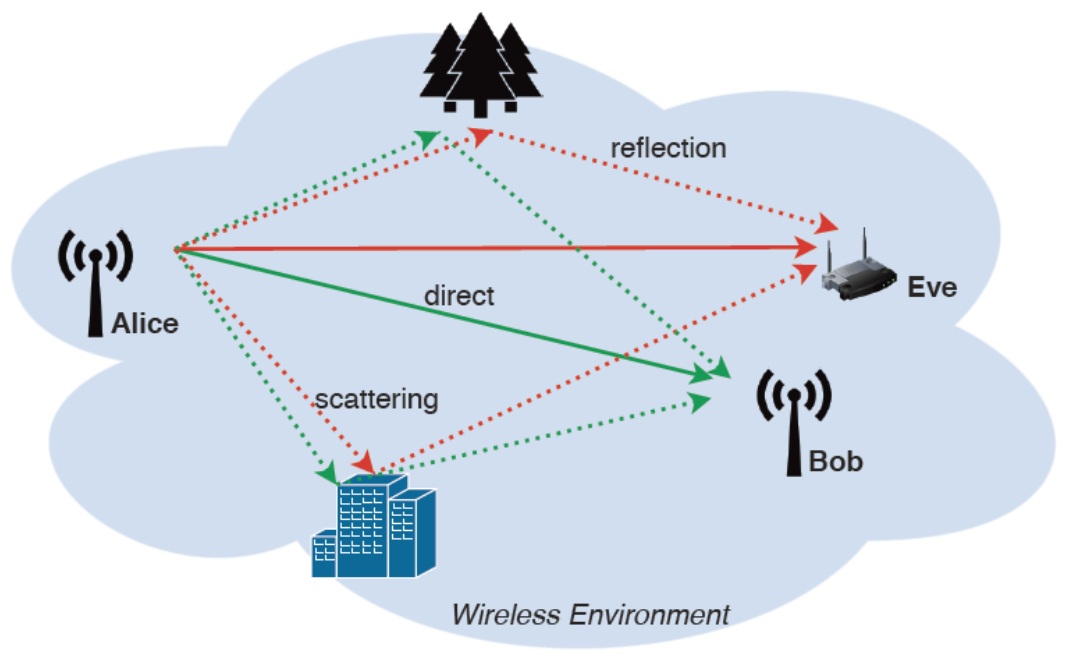
信源编码与信道转移矩阵
目录 一. 信息论模型 二. 点对点通信模型 三. 信源编码 四. 信道转移矩阵 4.1 二进制对称信道 4.2 二进制擦除信道 五. 小结 (1)信道直射与反射 (2)信道散射 (3) 信道时变性 一. 信息论模型 194…...

React 实现拖放功能
介绍 本篇文章将会使用react实现简单拖放功能。 样例 布局侧边栏拖放 LayoutResize.js import React, {useState} from "react"; import { Button } from "antd"; import "./LayoutResize.css";export const LayoutResize () > {const […...

马克思主义基本原理笔记
马克思主义哲学、政治经济学、科学社会主义理论 哲学 马克思主义中国化的理论成果:毛泽东思想、邓小平理论、三个代表重要思想、科学发展观 物质和意识哪个是本原,是哲学的基本问题 辩证法认为世界上的事物都是相互联系的、运动发展的,形…...
)
Vue+JavaSpingBoot笔记(1)
一、前后端通信参数问题 1.集合【字典】类型 Vue前端传递参数: export default {methods: { test(){// 将 filteredData 中的每一行值放入 newData 对象数组中 const newData filteredData.map(item > ({key1: item.Value1,key2: item.Value2,key3: "测试"}));r…...
)
10-单例模式(Singleton)
意图 保证一个类只有一个实例,并提供一个访问它的全局访问点 实现 1 懒汉式,线程不安全 public class Singleton { private static Singleton instance; private Singleton (){} public static Singleton getInstance() { if (instance null) {…...

C++ 求一个数是否是丑数。
#include<string.h> #include <iostream> using namespace std; int isChou(int num) { if (num < 0) { return 0; } while (num % 2 0) { // 不断除以2,直到不能整除为止 num / 2; } while (num % 3 0) { // 不断除…...
SpringCloud系列篇:核心组件之注册中心组件
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于SpringCloud的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.注册中心组件是什么 二.注册中心…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
