SQL ORDER BY 关键字
ORDER BY 关键字用于对结果集进行排序。
SQL ORDER BY 关键字
ORDER BY 关键字用于对结果集按照一个列或者多个列进行排序。
ORDER BY 关键字默认按照升序对记录进行排序。如果需要按照降序对记录进行排序,您可以使用 DESC 关键字。
SQL ORDER BY 语法
SELECT column1, column2, ... FROM table_name ORDER BY column1, column2, ... ASC|DESC;
- column1, column2, ...:要排序的字段名称,可以为多个字段。
- ASC:表示按升序排序。
- DESC:表示按降序排序。
相关文章:

SQL ORDER BY 关键字
ORDER BY 关键字用于对结果集进行排序。 SQL ORDER BY 关键字 ORDER BY 关键字用于对结果集按照一个列或者多个列进行排序。 ORDER BY 关键字默认按照升序对记录进行排序。如果需要按照降序对记录进行排序,您可以使用 DESC 关键字。 SQL ORDER BY 语法 SELECT …...

多线程-生产者消费者模型
一、基本信息 1、场景介绍:厨师和吃货的例子,吃货吃桌子上的面条,吃完让厨师做,厨师做完面条放桌子上,让吃货吃,厨师如果发现桌子上有面条,就不做,吃货发现桌子上没有面条就不吃。 …...

解压命令之一 gzip
文章目录 解压命令之一 gzip更多信息 解压命令之一 gzip gzip用于对后缀为gz文件进行解压: $ gzip -d data.gz这个命令将解压examplefile.gz,并且在当前目录下生成一个名为data的解压后的文件。 但特别需要留意的是,这个操作会删除源文件&…...
力扣:438. 找到字符串中所有字母异位词 题解
Problem: 438. 找到字符串中所有字母异位词 438. 找到字符串中所有字母异位词 预备知识解题思路复杂度Code其它细节推荐博客或题目博客题目滑动窗口哈希表 预备知识 此题用到了双指针算法中的滑动窗口思想,以及哈希表的运用。c中是unordered_map。如果对此不了解的u…...

QT 高DPI解决方案
一、根据DPI实现动态调整控件大小(三种方式) 1、QT支持高DPI(针对整个进程中所有的UI) // main函数中 QApplication::setAttribute(Qt::AA_EnableHighDpiScaling)tips:(1)如果不想全局设置&am…...

SLB、DMZ、Nginx、Ingress、Gateway、Kibana和Grafana
SLB、DMZ、Nginx、Ingress、Gateway、Kibana和Grafana虽然有一些相似之处,但是它们的功能和适用场景还是有所不同。 SLB主要用于将大流量的请求分配到多个服务器上进行处理,从而提高系统的可伸缩性和可靠性。它适用于需要处理大流量的应用,如…...

【已解决】Invalid bound statement (not found)
报错讯息 org.apache.ibatis.binding.BindingException: Invalid bound statement (not found): com.casey.mapper.SysRoleMapper.getUserRoleCode at org.apache.ibatis.binding.MapperMethod S q l C o m m a n d . < i n i t > ( M a p p e r M e t h o d . j a v a :…...
)
汽车信息安全--芯片厂、OEM安全启动汇总(1)
目录 1.芯驰E3安全启动 2.STM32 X-CUBE-SBSFU 3.小米澎湃OS安全启动 4.小结 我在前篇文章里详细记录了车规MCU信息安全设计过程关于网络安全架构的思考过程,从芯片原厂、供应商、OEM等角度思考如何建立起完备的信任链; 不过这思考过程仅仅只是一家之言,因此我又对比了国…...

气膜建筑:舒适、智能、可持续
气膜建筑之所以能够拥有广阔的发展空间,源于其融合了诸多优势特点,使其成为未来建筑领域的前沿趋势。 气膜建筑注重环境可持续性和能源效率。在材料和设计上,它采用可回收材料、提高热保温效果,并积极利用太阳能等可再生能源&…...
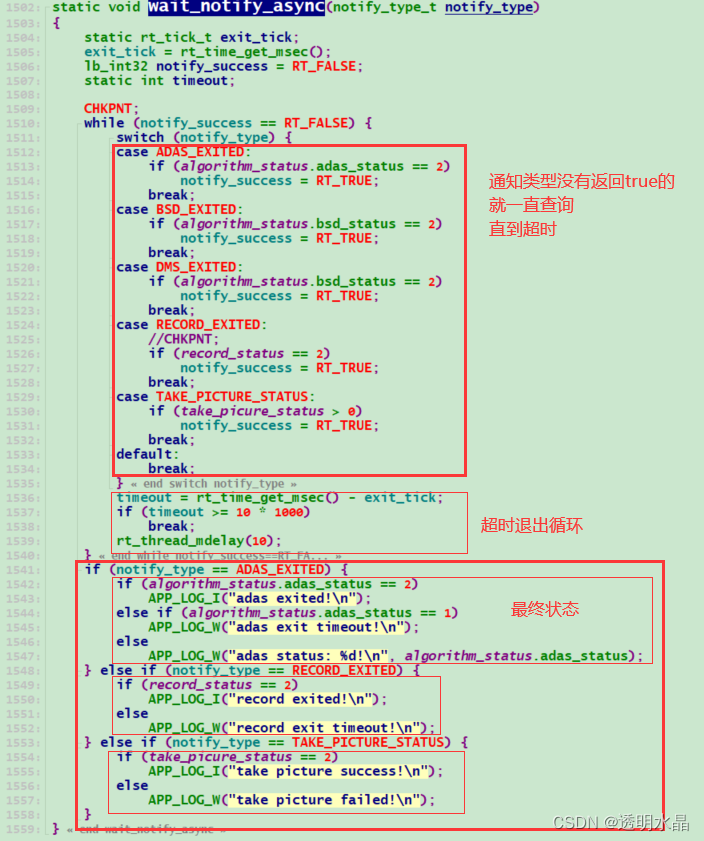
【C语言】一种状态超时阻塞循环查询的办法
【C语言】一种状态超时阻塞循环查询的办法 文章目录 【C语言】一种状态超时阻塞循环查询的办法1.方法12.方法21.方法1 static void wait_notify_async(notify_type_t notify_type) {static rt_tick_t exit_tick;exit_tick = rt_time_get_msec();lb_int32 notify_success = RT_F…...
【leetcode】力扣热门之回文链表【简单难度】
题目描述 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。 用例 输入:head [1,2,2,1] 输出:true 输入:head [1,2] 输出:f…...
巧用 sum(条件表达式) 语法)
【MySQL】ALL函数的巧用 以及 排序(order by)巧用 sum(条件表达式) 语法
力扣题 1、题目地址 578. 查询回答率最高的问题 2、模拟表 SurveyLog 表: Column NameTypeidintactionENUMquestion_idintanswer_idintq_numinttimestampint 这张表可能包含重复项。action 是一个 ENUM(category) 数据,可以是 “show”、“answer”…...
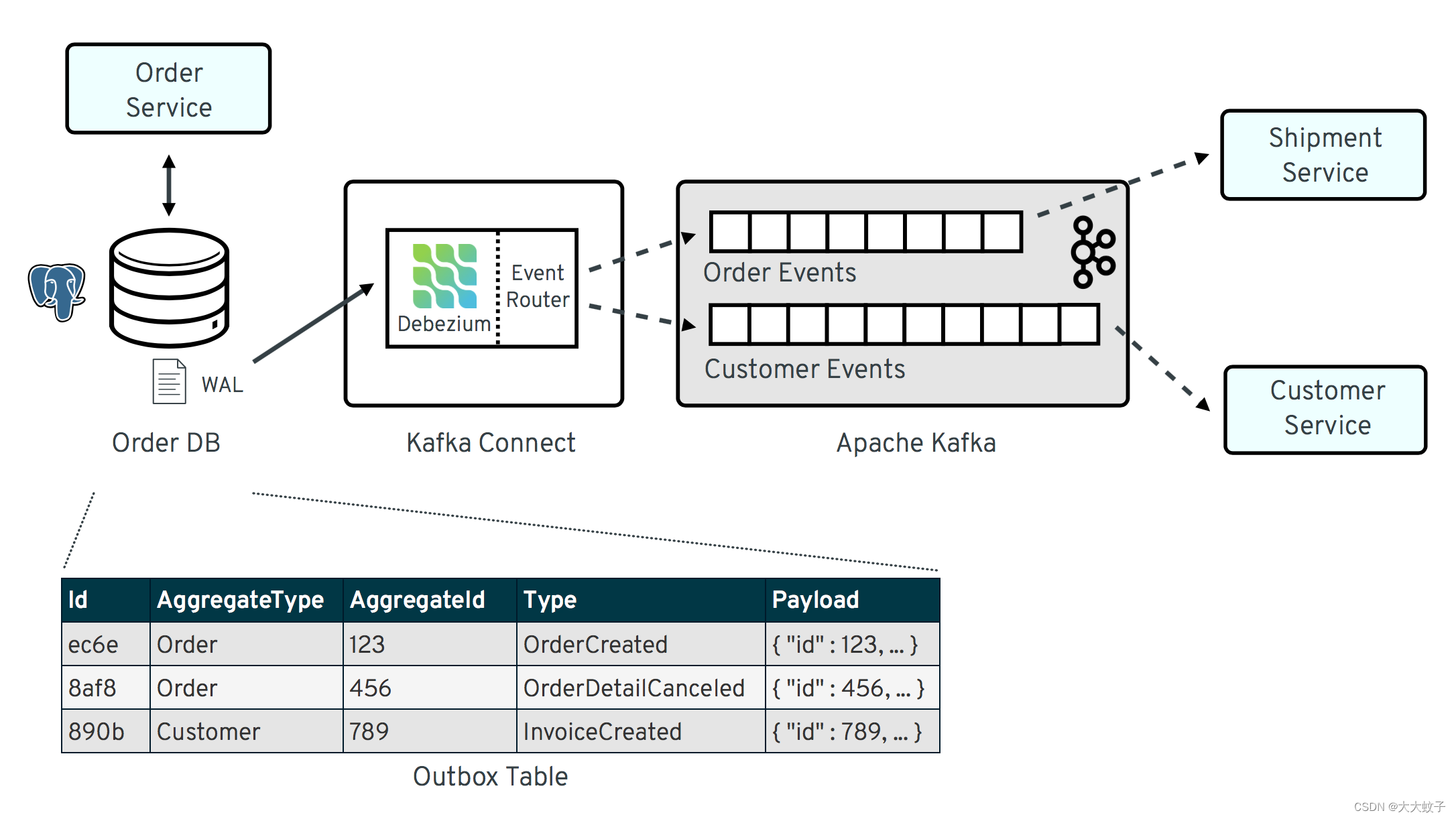
Debezium发布历史49
原文地址: https://debezium.io/blog/2019/02/19/reliable-microservices-data-exchange-with-the-outbox-pattern/ 欢迎关注留言,我是收集整理小能手,工具翻译,仅供参考,笔芯笔芯. 使用发件箱模式进行可靠的微服务数…...
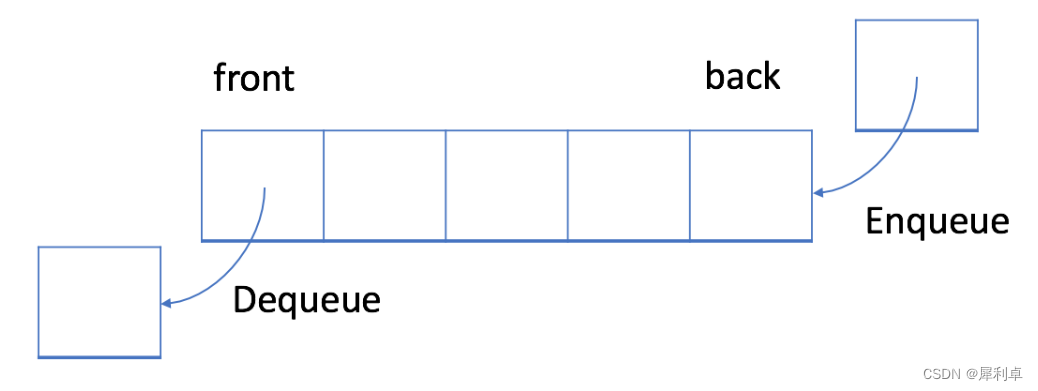
数据结构——队列(Queue)
目录 1.队列的介绍 2.队列工程 2.1 队列的定义 2.1.1 数组实现队列 2.1.2 单链表实现队列 2.2 队列的函数接口 2.2.1 队列的初始化 2.2.2 队列的数据插入(入队) 2.2.3 队列的数据删除(出队) 2.2.4 取队头数据 2.2.5 取队…...
uniapp微信小程序投票系统实战 (SpringBoot2+vue3.2+element plus ) -后端架构搭建
锋哥原创的uniapp微信小程序投票系统实战: uniapp微信小程序投票系统实战课程 (SpringBoot2vue3.2element plus ) ( 火爆连载更新中... )_哔哩哔哩_bilibiliuniapp微信小程序投票系统实战课程 (SpringBoot2vue3.2element plus ) ( 火爆连载更新中... )共计21条视频…...
两种方式实现mysql截取年月日
select date_format(now(), %Y-%m-%d) select substring(now(), 1, 10)...
WPF 使用矢量字体图标
矢量字体图标 在WPF项目中经常需要显示图标,但是项目改动后,有时候需要替换和修改图标,这样非常麻烦且消耗开发和美工的时间。为了快速开发项目,节省项目时间,使用图标矢量字体图标是一个非常不错的选择。 矢量字体图标…...

编程语言的语法糖,你了解多少?
什么是语法糖 语法糖是一种编程语言的特性,通常是一些简单的语法结构或函数调用,它可以通过隐藏底层的复杂性,并提供更高级别的抽象,从而使代码更加简洁、易读和易于理解,但它并不会改变代码的执行方式。 为什么需要语…...

MySQL中FLUSH TABLES命令语法
在MySQL中,FLUSH TABLES 命令的作用是刷新表。当你使用 FLUSH TABLES 命令的具体选项时(例如 FLUSH TABLES WITH READ LOCK),该选项必须是在 FLUSH 语句中唯一指定的命令。即,在一个 FLUSH 语句中,你只能使…...
如何在小米4A刷OpenWRT系统并通过cpolar实现公网访问本地路由器
文章目录 前言1. 安装Python和需要的库2. 使用 OpenWRTInvasion 破解路由器3. 备份当前分区并刷入新的Breed4. 安装cpolar内网穿透4.1 注册账号4.2 下载cpolar客户端4.3 登录cpolar web ui管理界面4.4 创建公网地址 5. 固定公网地址访问 前言 OpenWRT是一个高度模块化、高度自…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
