滑动窗口最大值:单调队列
239. 滑动窗口最大值
难度困难2154收藏分享切换为英文接收动态反馈
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 31 [3 -1 -3] 5 3 6 7 31 3 [-1 -3 5] 3 6 7 51 3 -1 [-3 5 3] 6 7 51 3 -1 -3 [5 3 6] 7 61 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= k <= nums.length
思路:单调队列
⚜️其实这道题的解法有不同种形式,但是绕不开的就是使用单调队列的思想,为什么呢❓❓❓
因为如果这个时候我们不用单调队列的话,就是说我们每次去控制这个窗口里面的最大值,如果这个窗口很大,那么时间复杂度是非常高的,因为遍历一遍这个窗口获取最大值的时间复杂度是 O(k),而我们还得去遍历这个数组的元素,那么总和起来就是 O(n*k),这样子在这道题是会超时的!所以我们得使用单调队列的思想!
那么我们得先了解一下,什么是单调队列!
什么是单调队列
单独队列本质还是一个队列,只是我们规定这个队列是一个单调递减或者单调递增队列!⚜️单调递减和递增是什么意思呢❓❓❓
这里以单调递减为例,因为和我们这道题比较符合!我们举一个数学上面的例子 y = ax + b,我们知道递减就是函数在某个区间上面的 y 随着 x 的增大,而不断的减小或者相等,但是如果我们定义它为单调递减,那么这个函数则变成在 整个区间上面都是 y 随着 x 的增大而不断的减小!
一般来说,单调队列使用 C++ 中的 deque 来实现会更好,因为其支持双端的插入删除以及获取双端元素!
⚜️那么这道题要使用单调递减还是单调递增呢❓❓❓
其实用单调递减会更加的符合滑动窗口的原理,我们保持从队头的元素开始,每个元素都大于其后面的元素,这样子像下图一样:
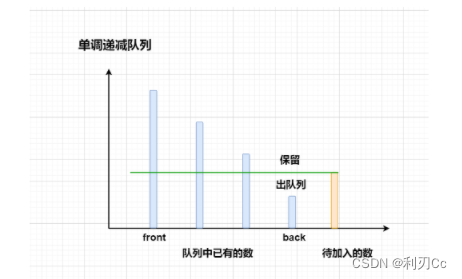
也就是我们**保持让队头的元素是整个队列里面最大的**!
⚜️这样子有什么好处呢❓❓❓
我们每次取当前窗口的最大值,那么就和这个队头元素有关系啦,但是我们得来维护一下这个队列,而不同方式维护就有了不同的实现方法,下面我们举两种方法,其中我觉得最好理解的就是第一种!
1、队列维护数组下标
滑动窗口最大值 | 图解单调队列 | 最清晰易懂的讲解【c++/java】
⚜️为什么要维护数组的下标呢❓❓❓
因为每次我们需要去控制这个窗口移动,并保持让队列中的元素都落于这个窗口内,所以我们得一直关注着队列中的元素的值是在 nums 数组中的哪个位置,会不会出界,这些问题都要考虑,所以我们干脆直接用队列来保存其数组的下标,然后比较大小也是非常方便,因为是数组,所以有了下标,我们直接通过 nums[i] 就能快速索引到对应的元素,根本不用担心效率问题!并且这样子也非常的好控制!
下面我们来看看具体的步骤(下面步骤中默认我们的队列变量名叫做dq):
- 遍历 nums 数组的每个元素
- 每次遍历元素的时候,先循环判断一下队头元素在nums中位置是否已经掉出了窗口范围
- 如果
i - k + 1 > dq.front(),说明队头元素已经不落在该窗口内了,我们就将队头pop掉!否则不用。- (值得解释一下的是这里的
i - k + 1其实代表的就是窗口的第一个元素下标,也就是窗口的头位置!其中 dq.front() 代表的是队头元素在 nums 中的下标,如果我们的窗口头位置都超过了这个队头元素的下标了,那么说明这个队头元素不是当前窗口内的!) - (还有值得注意的是这里可以进行循环判断,也可以不进行循环判断,因为我们每次都只会对 i 进行一次的 ++,但是为了代码上面看起来严谨,可以将其改为循环判断!)
- (值得解释一下的是这里的
- 如果
- 控制新元素 nums[i] 加入的时候保持单调递减队列的规则
- 如果
nums[i] > dq.back(),此时如果直接将 nums[i] 加入队列的话,会破坏单调递减的规则,所以我们要将 dq.back() 进行删除,并且不断循环判断,直到队列为空,或者遇到比 nums[i] 小或者等于的值为止!
- 如果
- 将 nums[i] 加入单调队列
- 最后判断一下是否已经到了满足窗口大小 k 的位置了
- 是的话则开始向数组 v 中 push 进每次窗口最大的元素,也就是队头元素在 nums 中对应位置的元素!
💥**注意:队列中队头元素不一定是最大的,因为存放的不是数组中元素的值,而是其最大元素的下标!**
其实这道题是相对比较复杂的,最好是自己先模拟这个过程!
下面给出代码:
class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {vector<int> v;deque<int> dq;for(int i = 0; i < nums.size(); ++i){// 1、控制窗口的元素大小不大于k个,若大于则pop掉队头while(dq.size() > 0 && i - k + 1 > dq.front())dq.pop_front();// 2、控制新元素加入的时候保持单调递减队列的规则// 若新元素大于其队尾的元素,那么则pop掉该元素,直到遇到比新元素大或者相等为止while(dq.size() > 0 && nums[i] > nums[dq.back()])dq.pop_back();// 3、将新元素加入队列dq.push_back(i);// 4、若其循环到满足窗口大小k的位置了,则开始向v中push进每次最大的元素,也就是队头元素// 其中因为i是下标而k是大小,所以i要加一if(i + 1 >= k)v.push_back(nums[dq.front()]);}return v;}
};
2、队列维护数组元素值
[C++]滑动窗口最大值–单调队列
这种方法可能是我们会比较先于维护数组下标而想到的,因为通常来说我们都会先去想怎么存放这个值,而不是存放对应下标,也确实,这道题如果是维护元素的值,那么相对于第一种方法来说会更容易出错一点,因为我们得去控制这个窗口移动的时候于队列元素的关系,保持其一直是窗口内有效元素!
既然队列要维护数组元素值,那么当然队头元素就和第一种方法不一样了,这次队头元素肯定是队列里面最大的,因为这是一个单调队列,并且其存放的本身就是元素的值而不是下标!
💥下面是步骤:
- 首先可以维护队列保持单调递减,将 nums[i] 和队尾元素进行比较,若 dq.back() < nums[i] 说明需要 pop 掉队尾元素,和方法一类似!
- 将新元素加入队列
- 若其循环到满足窗口大小 k 的位置了,则开始向 v 中 push 进每次最大的元素,也就是队头元素,和方法一类似!
- 注意还要维护队列元素是否在窗口内有效(因为要进行 nums 索引,所以最好放到第三步这个判断语句中比较安全)
其实和第一种方法大同小异,不同的就是它们的大小判断等等,最重要的是这个第四步,也就是控制这个队列中队头等元素是否还在合法的窗口区间内,如果不是的话则要进行删除,而我们并不容易判断这个区间,因为我们怎么知道队头元素对应 nums 中的下标呢❓❓❓
其实这就是一个难点,所以我们要改变思路:
💥因为每次我们只让 i 累加一次,也就是每次遍历只会让 i 向后走一步,那么我们只需要跟着遍历每次的窗口第一个元素,是否和当前队头的元素一样,一样的话说明遍历下一个元素的时候,这个元素就已经不再是窗口内的元素了,所以我们就把这个队头元素给 pop 掉!而这个窗口的头位置就是 i-k+1 处,但是由于窗口一开始还没达到 k 个,所以要建立在条件是 i+1 >= k 的基础之上!
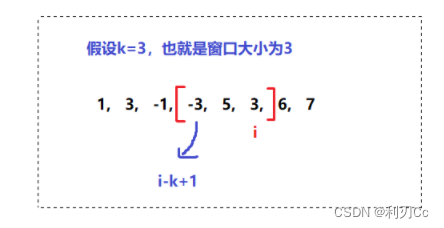
class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {vector<int> v;deque<int> dq;for(int i = 0; i < nums.size(); ++i){// 1、首先可以维护队列保持单调递减,将nums[i]和队尾元素进行比较while(dq.size() > 0 && dq.back() < nums[i])dq.pop_back();// 2、将新元素加入队列dq.push_back(nums[i]);// 3、若其循环到满足窗口大小k的位置了,则开始向v中push进每次最大的元素,也就是队头元素// 其中因为i是下标而k是大小,所以i要加一if(i + 1 >= k){v.push_back(dq.front());// 4、注意还要维护队列元素(因为要进行nums索引,所以最好放到if(i+1>=k)这个判断语句中比较安全)if(dq.size() > 0 && dq.front() == nums[i - k + 1])dq.pop_front();}}return v;}
};
相关文章:

滑动窗口最大值:单调队列
239. 滑动窗口最大值 难度困难2154收藏分享切换为英文接收动态反馈 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例…...

负载均衡算法
静态负载均衡 轮询 将请求按顺序轮流地分配到每个节点上,不关心每个节点实际的连接数和当前的系统负载。 优点:简单高效,易于水平扩展,每个节点满足字面意义上的均衡; 缺点:没有考虑机器的性能问题&…...
C语言数组二维数组
C 语言支持数组数据结构,它可以存储一个固定大小的相同类型元素的顺序集合。数组是用来存储一系列数据,但它往往被认为是一系列相同类型的变量。 数组的声明并不是声明一个个单独的变量,比如 runoob0、runoob1、…、runoob99,而是…...
7年测试工程师,裸辞掉17K的工作,想跳槽找更好的,还是太高估自己了....
14年大学毕业后,在老师和朋友的推荐下,进了软件测试行业,这一干就是7年时间,当时大学本来就是计算机专业,虽然专业学的一塌糊涂,但是当年的软件测试属于新兴行业,人才缺口比较大,而且…...

企业为什么需要做APP安全评估?
近几年新型信息基础设施建设和移动互联网技术的不断发展,移动APP数量也呈现爆发式增长,进而APP自身的“脆弱性”也日益彰显,这对移动用户的个人信息及财产安全带来巨大威胁和挑战。在此背景下,国家出台了多部法律法规,…...

重回利润增长,涪陵榨菜为何能跑赢周期?
2022年消费市场持续低迷,疫情寒冬之下,不少食品快消企业均遭遇严重的业绩下滑,但一年里不断遭遇利空打击的“榨菜茅”涪陵榨菜,不仅安然躲过“酸菜劫”、走出“钠”争议,而且顺利将产品价格提起来,并在寒冬…...

这6个高清图片素材库,马住,马住~
网上找的图片素材清晰度不够,版权不明确怎么办。看看这几个可商用图片素材网站,解决你的所有图片需求,高清无水印,赶紧马住! 1、菜鸟图库 美女图片|手机壁纸|风景图片大全|高清图片素材下载网 - 菜鸟图库 网站素材…...
)
绝对零基础的C语言科班作业(期末模拟考试)
编程题(共10题; 共100.0分)模拟1(输出m到n的素数)从键盘输入两个整数[m,n], 输出m和n之间的所有素数。 输入样例:3,20输出样例:3 5 7 11 13 17 19 (输出数据之间用空格间…...

注解开发定义bean
注解开发定义bean 使用Component定义bean在核心配置文件中通过组件扫描加载bean,需要指定扫描包的范围 当然也可以使用Component的衍生注解,可以更加形象的表示 纯注解的开发模式 使用java类来代替了以前的 配置文件,在java类中ÿ…...

剑指 Offer 19. 正则表达式匹配
摘要 剑指 Offer 19. 正则表达式匹配 请实现一个函数用来匹配包含. 和*的正则表达式。模式中的字符.表示任意一个字符,而*表示它前面的字符可以出现任意次(含0次)。在本题中,匹配是指字符串的所有字符匹配整个模式。例如&#x…...
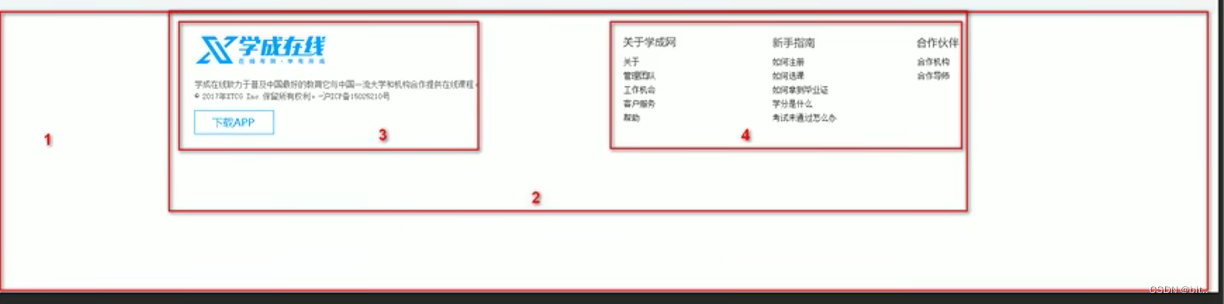
CSS——学成在线案例
🍓个人主页:bit.. 🍒系列专栏:Linux(Ubuntu)入门必看 C语言刷题 数据结构与算法 HTML和CSS3 目录 1.案例准备工作 2.CSS属性书写顺序(重点) 3.页面布局整体思路 4.头部的制作编辑 5.banner制作…...

元数据的类型
元数据通常分为三种类型:业务元数据、技术元数据和操作元数据。这些类别使人们能够理解属于元数据总体框架下的信息范围,以及元数据的产生过程。也就是说,这些类别也可能导致混淆,特别是当人们对一组元数据属于哪个类别或应该由谁…...
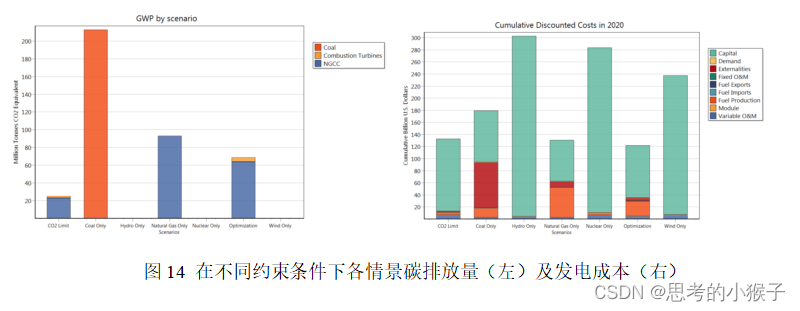
LEAP模型的能源环境发展、碳排放建模预测及不确定性分析
LEAP(Long Range Energy Alternatives Planning System/ Low emission analysis platform,长期能源可替代规划模型)是一种自下而上的能源-环境核算工具,由斯德哥尔摩环境研究所和美国波士顿大学联合研发。该模型与情景分析法紧密结…...

C# Task详解
1、Task产生背景 Task出现之前,微软的多线程处理方式有:Thread→ThreadPool→委托的异步调用,虽然也可以基本业务需要的多线程场景,但它们在多个线程的等待处理方面、资源占用方面、线程延续和阻塞方面、线程的取消方面等都显得比…...

Blob分析+特征
Blob分析特征0 前言1 概念2 方法2.1 图像采集2.2 图像分割2.3 特征提取3 主要应用场景:0 前言 在缺陷检测领域,halcon通常有6种处理方法,包括Blob分析特征、Blob分析特征差分、频域空间域、光度立体法、特征训练、测量拟合,本篇博…...
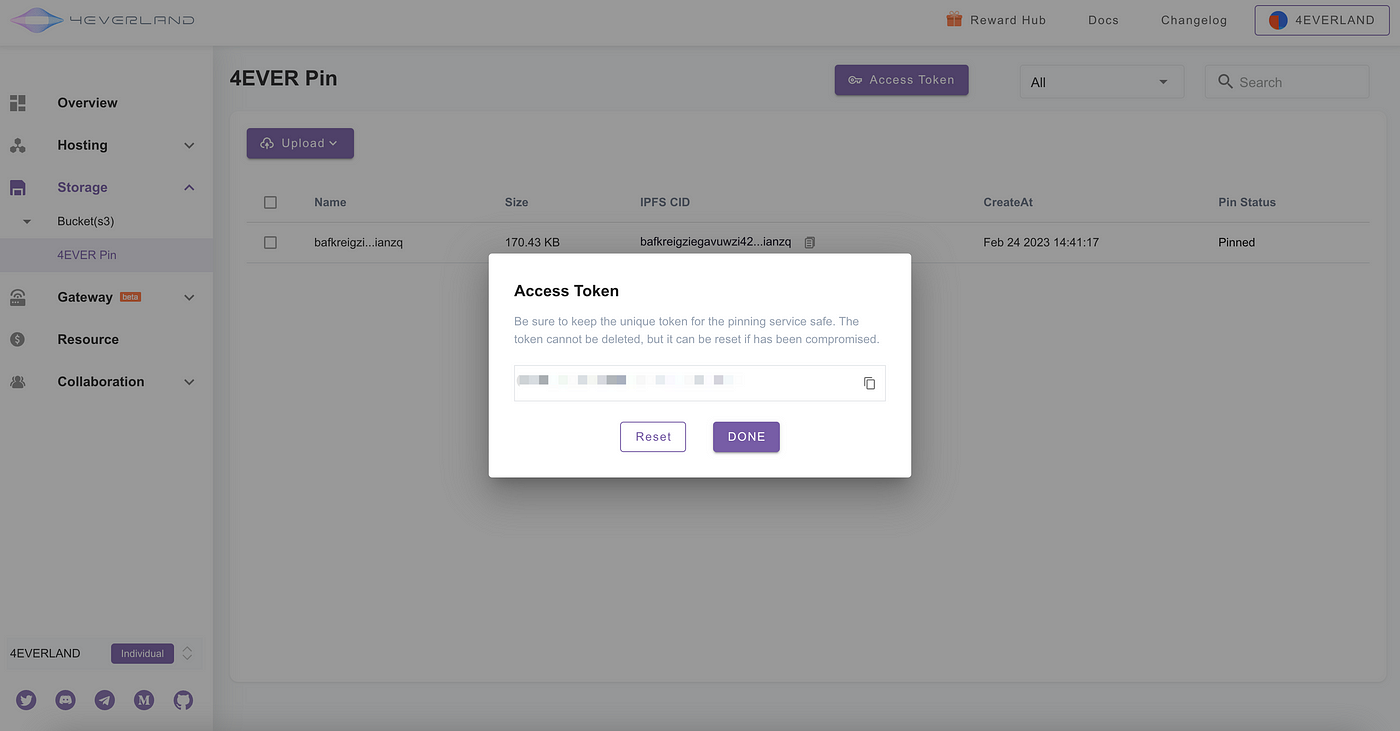
4EVERLAND 的 IPFS Pinning 服务:4EVER Pin
我们很高兴地宣布 4EVERLAND Storage 的一个令人兴奋的补充,即 4EVER Pin。什么是 4EVER Pin?您可能已经知道星际文件系统或IPFS是一个分布式存储网络,来自世界各地的计算机组成节点共享数据。通常,在IPFS中获取一条数据时&#x…...

activiti整合springBoot其他操作
如果单纯使用activiti进行流程的自动控制,是可以实现的。但是通常我们都需要结合自定义的表,便于在流程执行中更加清晰的看到每一个流程实例节点的具体信息。关联自定义表与activiti表才能完成真正的业务 BusinessKey关联 // 定义businessKey Test pub…...

深度探索C++预编译头机制
深度详见预编译头,以vs编译器实现的预编译头管理为例 预编译头是为了节省庞大的编译时间,采取的一种方法;C标准并没有规定如何实现预编译头机制;因此其具体实现方式由编译器供应商自行决定。 下面就以VS中观测的结果为例进行说明…...
Leaflet基础入门教程(一)
leaflet是一个前端的轻量的gis框架,为什么说它轻量呢。因为相比于传统的“庞大的”GIS框架比如openlayers和mapbox,leaflet不仅代码体积小,而且API构成也极为简单。是GIS行业小白入门级别学习的最好的框架,没有之一。 那么话不多说我们首先来学习一下如何使用leaflet搭建一…...

《强化学习导论》之6.5 Q-Learning
Q-Learning:Off-Policy TD Control强化学习的早期突破之一是开发了一种称为Q学习的非策略TD控制算法(Watkins,1989)。其最简单的形式,定义为(6.8)在这种情况下,学习的动作-值函数Q直接近似于最优动作-值函数࿰…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
