均匀与准均匀 B样条算法
B 样条曲线的定义
p ( t ) = ∑ i = 0 n P i F i , k ( t ) p(t) = \sum_{i=0}{n} P_i F_{i, k}(t) p(t)=i=0∑nPiFi,k(t)
方程中 n + 1 n+1 n+1 个控制点, P i P_i Pi, i = 0 , 1 , ⋯ n i=0, 1, \cdots n i=0,1,⋯n 要用到 n + 1 n+1 n+1 个 k k k 次 B 样条基函数 F i , k F_{i, k} Fi,k, i = 0 , 1 , ⋯ , n i=0, 1, \cdots, n i=0,1,⋯,n, 节点矢量为 T = [ t 0 , t 1 , ⋯ , t n + k + 1 ] T = [t_0, t_1, \cdots, t_{n+k+1}] T=[t0,t1,⋯,tn+k+1]。 F i , k ( t ) F_{i, k}(t) Fi,k(t) 是由一个称为节点矢量的非递减的参数 t t t 的序列, t 0 ≤ t 1 ≤ ⋯ ≤ t n + k + 1 t_0 \leq t_1 \leq \cdots \leq t_{n+k+1} t0≤t1≤⋯≤tn+k+1所决定的 k k k 次分段多项式。
B 样条曲线划分为四种类型,均匀 B 样条曲线,准均匀B 样条曲线,分段 Bezier 曲线和非均匀 B 样条曲线。
定义域
给定 n + 1 n+1 n+1 个控制点, P i P_i Pi, i = 0 , 1 , ⋯ n i=0, 1, \cdots n i=0,1,⋯n, 相应地要求 n + 1 n+1 n+1 个 B 样条基函数 F i , k ( t ) F_{i, k}(t) Fi,k(t) 定义一个 k k k 次 B 样条曲线,这 n + 1 n+1 n+1 个 k k k 次 B 样条由节点矢量 T = [ t 0 , t 1 , ⋯ t n + k + 1 ] T = [t_0, t_1, \cdots t_{n+k+1}] T=[t0,t1,⋯tn+k+1] 所决定。
并非这个些节点矢量所包含的 n + k + 1 n+k +1 n+k+1 个区间都在该曲线的定义域,其中两端的各 k k k 个几点区间,不能作为 B 样条曲线的定义区间。
这是因为 n + 1 n+1 n+1 个控制点中最前的 n + 1 n+1 n+1 个顶点 P i P_i Pi, i = 0 , 1 , ⋯ k i=0,1, \cdots k i=0,1,⋯k 定义了 B 样条曲线的首段,其定义区间为 t ∈ [ t k , t k + 1 ] t\in [t_k, t_{k+1}] t∈[tk,tk+1] 往后移动一个顶点 P i P_i Pi, i = 1 , 2 , ⋯ k + 1 i=1, 2, \cdots k+1 i=1,2,⋯k+1 定义第二段,其定义区间为 t ∈ [ t k + , t k + 2 ] t \in [t_{k+}, t_{k+2}] t∈[tk+,tk+2] 依次类推,最后 k + 1 k+1 k+1 个顶点, P i P_i Pi, i = n − k , b − k − 1 , ⋯ n i=n-k, b-k-1, \cdots n i=n−k,b−k−1,⋯n 定义最后一段,其定义区间为 t ∈ [ t n , t n + 1 ] t\in[t_n, t_{n+1}] t∈[tn,tn+1], 因此,高于零次的 k k k 次B 样条曲线的定义域为
t ∈ [ t k , t n + 1 ] t \in [t_k, t_{n+1}] t∈[tk,tn+1]
三次均匀 B 样条曲线
{ F 0 , 3 ( t ) = 1 6 ( 1 − t ) 3 = ( − t 3 + 3 t 2 − 3 t + 1 ) F 1 , 3 ( t ) = 1 6 ( 3 t 3 − 6 t 2 + 4 ) F 2 , 3 ( t ) = 1 6 ( − 3 t 3 + 3 t 2 + 3 t + 1 ) F 3 , 3 ( t ) = 1 6 t 3 \begin{cases} F_{0,3}(t) = \frac{1}{6} (1-t)^3 = (-t^3 + 3t^2 -3t+1)\\ F_{1,3}(t) = \frac{1}{6} (3t^3 - 6t^2 +4)\\ F_{2,3}(t) = \frac{1}{6} (-3t^3 + 3t^2 + 3t +1) \\ F_{3,3}(t) = \frac{1}{6} t^3\\ \end{cases} ⎩ ⎨ ⎧F0,3(t)=61(1−t)3=(−t3+3t2−3t+1)F1,3(t)=61(3t3−6t2+4)F2,3(t)=61(−3t3+3t2+3t+1)F3,3(t)=61t3


三次 B 样条的几何性质
{ p ( 0 ) = 1 6 ( p 0 + 4 p 1 + p 2 ) = 1 3 ( p 0 + p 2 2 ) + 2 3 p 1 = 1 3 p m + 2 3 p 1 p ( 1 ) = 1 6 ( p 1 + 4 p 2 + p 3 ) = 1 3 ( p 1 + p 3 2 ) + 2 3 p 2 = 1 3 p n + 2 3 p 2 \begin{cases} p(0) = \frac{1}{6}(p_0 + 4 p_1 + p_2) = \frac{1}{3} (\frac{p_0 + p_2}{2}) + \frac{2}{3}p_1 = \frac{1}{3}p_m + \frac{2}{3}p_1\\ p(1) = \frac{1}{6}(p_1 + 4 p_2 + p_3) = \frac{1}{3} (\frac{p_1 + p_3}{2}) + \frac{2}{3}p_2 = \frac{1}{3}p_n + \frac{2}{3}p_2\\ \end{cases} {p(0)=61(p0+4p1+p2)=31(2p0+p2)+32p1=31pm+32p1p(1)=61(p1+4p2+p3)=31(2p1+p3)+32p2=31pn+32p2
{ p ′ ( 0 ) = 1 2 ( p 2 − p 0 ) p ′ ( 1 ) = 1 2 ( p 3 + p 1 ) \begin{cases} p'(0) = \frac{1}{2}(p_2 - p_0) \\ p'(1) = \frac{1}{2}(p_3 + p_1) \\ \end{cases} {p′(0)=21(p2−p0)p′(1)=21(p3+p1)
{ p ′ ′ ( 0 ) = p 0 − 2 p 1 + p 2 = 2 ( p 0 + p 2 2 − p ) = 2 ( p m − p 1 ) p ′ ′ ( 1 ) = p 1 − 2 p 2 + p 3 = 2 ( p 1 + p 3 2 − p 2 ) = 2 ( p n − p 2 ) \begin{cases} p''(0) = p_0 - 2p_1 + p_2 = 2(\frac{p_0 + p_2}{2} -p)= 2(p_m - p_1) \\ p''(1) = p_1 - 2p_2 + p_3 = 2(\frac{p_1 + p_3}{2} -p_2)= 2(p_n - p_2) \\ \end{cases} {p′′(0)=p0−2p1+p2=2(2p0+p2−p)=2(pm−p1)p′′(1)=p1−2p2+p3=2(2p1+p3−p2)=2(pn−p2)

#include <QWidget>
#include <QApplication>
#include <QPainter>
#include <QPointF>
#include <QPainterPath>const double knot[13] = {-3/6.0, -2/6.0, -1/6.0, 0.0, 1 / 6.0, 2 / 6.0, 3 / 6.0, 4 / 6.0, 5 / 6.0, 1.0, 7/ 6.0, 8/ 6.0, 9/6.0};double BasisFunctionValue(double t, int i, int k)
{double val1, val2, val;if (k == 0){if ((t >= knot[i]) && t < knot[i + 1]){return 1.0;}else{ // 其它return 0.0;}}if (k > 0){if (t < knot[i] || t > knot[i + k + 1]) {return 0.0; // 其它}else{double coffcient1, coffcient2; // 凸组合系数1 凸组合系数 2double denominator = 0.0; // 分母denominator = knot[i + k] - knot[i];if (denominator == 0.0){// 约定 0/0 = 0coffcient1 = 0.0;}else{coffcient1 = (t - knot[i]) / denominator; // 计算的第一项}denominator = knot[i + k + 1] - knot[i + 1]; // 递推公式第二项分母if (denominator == 0.0){// 约定 0/0 = 0coffcient2 = 0.0;}else{coffcient2 = (knot[i + k + 1] - t) / denominator; // 递推公式第二项}val1 = coffcient1 * BasisFunctionValue(t, i, k - 1); // 递推公式第一项的只val2 = coffcient2 * BasisFunctionValue(t, i+1, k - 1); // 递推公式第二项的只val = val1 + val2; // 基函数的值}}return val;
}void drawBSplineCure(QPainter* painter, const std::vector<QPointF>& P)
{// Set line colorQColor lineColor(0, 0, 255);// Set point colorQColor pointColor(255, 0, 0);QPainterPath bezierPath;QPen pen(lineColor);pen.setWidth(2); // Set the line width as neededpainter->setPen(pen);QPointF center(900, 600); // Center coordinatesint k = 3; // Degree of the B-spline curvefor (int i = k; i <= P.size() - k; ++i){double tStep = 0.01;for (double t = 0.0; t <= 1.0; t += tStep){QPointF p(0, 0); // Discrete pointfor (int j = 0; j < P.size(); ++j){double BValue = BasisFunctionValue(t, j, k);p += P[j] * BValue;}if (t == 0.0){bezierPath.moveTo(p + center);}else{bezierPath.lineTo(p + center);}painter->setPen(pointColor);painter->setBrush(Qt::NoBrush);painter->drawEllipse(p + center, 5, 5);}}painter->drawPath(bezierPath);
}void drawControlPolygon(QPainter* painter, std::vector<QPointF> P)
{QColor lineColor(0, 0, 0);QColor pointColor(0, 0, 255); // Blue color for pointsQPen polyLinePen(lineColor);painter->setPen(polyLinePen);QBrush pointBrush(pointColor);painter->setBrush(pointBrush);QPointF center(900, 600);QVector<QPointF> shiftedPoints;std::transform(P.begin(), P.end(), std::back_inserter(shiftedPoints),[center](const QPointF& point) { return point + center; });painter->drawPolyline(shiftedPoints.data(), shiftedPoints.size());for (const QPointF& point : shiftedPoints){painter->drawEllipse(point, 5, 5);}}std::vector<QPointF> getControlPoints(){std::vector<QPointF> controlPoints = {QPointF(-600, -50),QPointF(-500, 200), // 控制点QPointF(-160, 250),QPointF(-250, -300),QPointF(160, -200), // 控制点QPointF(200, 200),QPointF(600, 180),QPointF(700, -60), // 控制点QPointF(500, -200)};return controlPoints;
}class MyWidget : public QWidget {
public:MyWidget(QWidget* parent = nullptr) : QWidget(parent) {setFixedSize(1800, 1200);}protected:void paintEvent(QPaintEvent* event) override {Q_UNUSED(event);QPainter painter(this);painter.setRenderHint(QPainter::Antialiasing, true);std::vector<QPointF> controlPoints = getControlPoints();drawBSplineCure(&painter, controlPoints);drawControlPolygon(&painter, controlPoints);}public:int n = 8;int k = 3;};int main(int argc, char* argv[]) {QApplication app(argc, argv);MyWidget widget;widget.show();return app.exec();
}
相关文章:

均匀与准均匀 B样条算法
B 样条曲线的定义 p ( t ) ∑ i 0 n P i F i , k ( t ) p(t) \sum_{i0}{n} P_i F_{i, k}(t) p(t)i0∑nPiFi,k(t) 方程中 n 1 n1 n1 个控制点, P i P_i Pi, i 0 , 1 , ⋯ n i0, 1, \cdots n i0,1,⋯n 要用到 n 1 n1 n1 个 k k k 次 B 样条基函数 …...
答案解析)
2023年12 月电子学会Python等级考试试卷(一级)答案解析
青少年软件编程(Python)等级考试试卷(一级) 分数:100 题数:37 一、单选题(共25题,共50分) 1. 下列程序运行的结果是?( ) print(hello) print(world) A. helloworld...
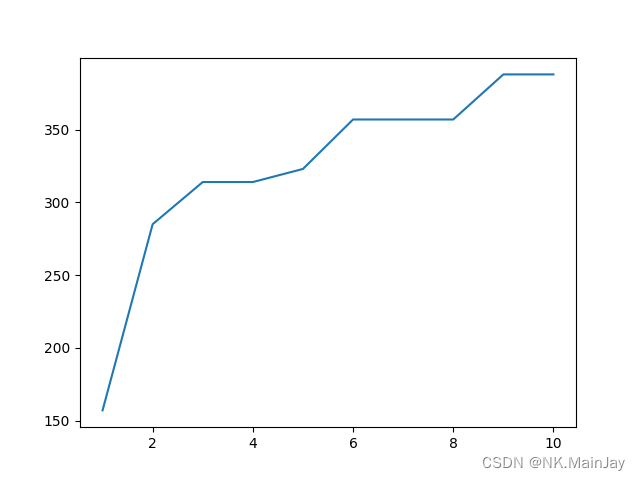
启发式算法解决TSP、0/1背包和电路板问题
1. Las Vegas 题目 设计一个 Las Vegas 随机算法,求解电路板布线问题。将该算法与分支限界算法结合,观察求解效率。 代码 python代码如下: # -*- coding: utf-8 -*- """ Date : 2024/1/4 Time : 16:21 Author : …...

阿里云新用户的定义与权益
随着云计算的普及,阿里云作为国内领先的云计算服务提供商,吸引了越来越多的用户。对于新用户来说,了解阿里云新用户的定义和相关权益非常重要,因为它关系到用户能否享受到更多的优惠和服务。 一、阿里云新用户的定义 阿里云新用户…...

go语言多线程操作
目录 引言 一、如何实现多线程 1. 线程的创建与管理: 2. 共享资源与同步: 3. 线程间通信: 4. 线程的生命周期管理: 5. 线程安全: 6. 考虑并发问题: 7. 性能与资源利用: 8. 特定语言或框架的工具和库: 二、go语言多线程 Goroutine 1. 轻量级: 2. 动态栈: 3. 调度:…...

GreatSQL社区2023全年技术文章总结
GreatSQL社区自成立以来一直致力于为广大的数据库爱好者提供一个交流与学习的平台。在2023年,我们见证了社区的蓬勃发展,见证了众多技术文章的诞生与分享。 此篇总结呈现GreatSQL社区2023年社区技术文章在CSDN发布的全部。这些文章涵盖了GreatSQL、MGR、…...

【论文阅读笔记】Stable View Synthesis 和 Enhanced Stable View Synthesis
目录 Stable View Synthesis摘要引言 Enhanced Stable View Synthesis 从Mip-NeRF360的对比实验中找到的两篇文献,使用了卷积神经网络进行渲染和新视角合成,特此记录一下 ToDo Stable View Synthesis paper:https://readpaper.com/pdf-ann…...
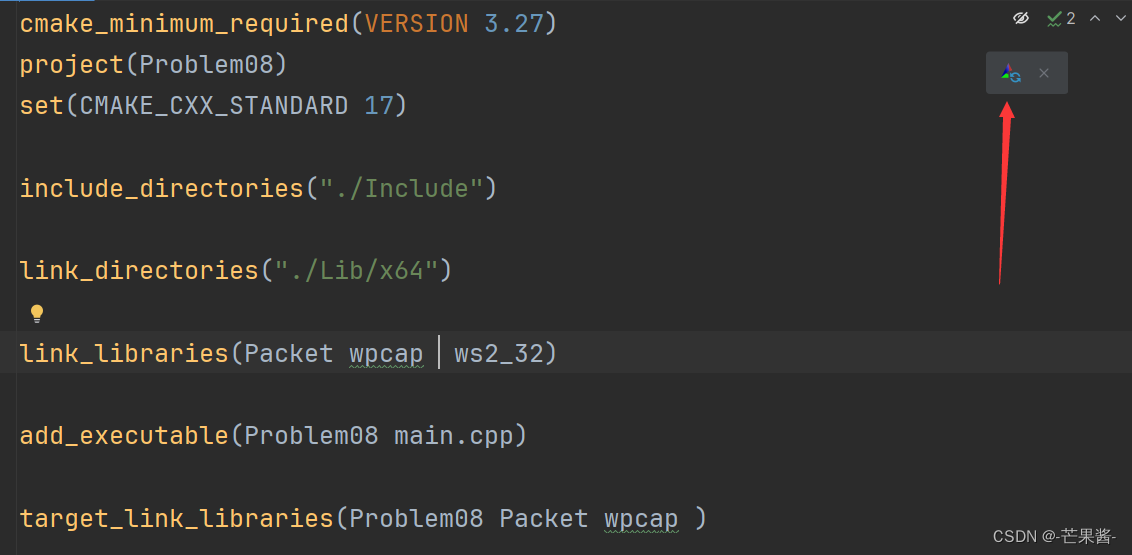
网络报文分析程序的设计与实现(2024)
1.题目描述 在上一题的基础上,参照教材中各层报文的头部结构,结合使用 wireshark 软件(下载地址 https://www.wireshark.org/download.html#releases)观察网络各层报文捕获,解析和分析的过程(如下 图所示&a…...
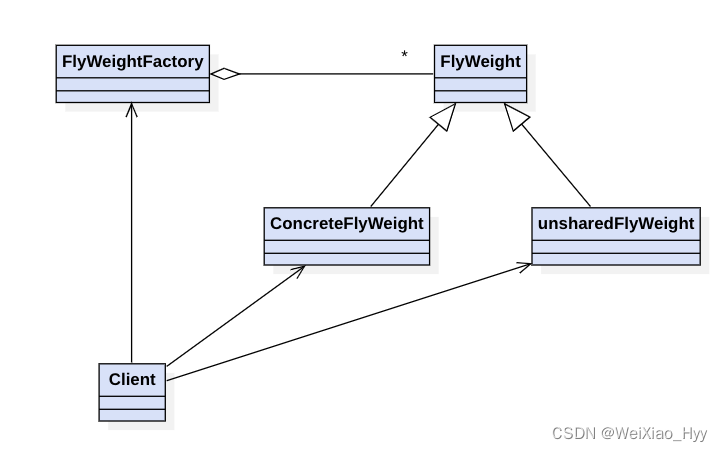
贯穿设计模式-享元模式思考
写享元模式的时候,会想使用ConcurrentHashMap来保证并发,没有使用双重锁会不会有问题?但是在synchronize代码块里面需要尽量避免throw异常,希望有经验的同学能够给出解答? 1月6号补充:没有使用双重锁会有问…...
)
牛客刷题:BC45 小乐乐改数字(中等)
自我介绍:一个脑子不好的大一学生,c语言接触还没到半年,若涉及到效率等问题,各位都可以在评论区提出见解,谢谢啦。 该账号介绍:此帐号会发布游戏(目前还只会简单小游戏),…...
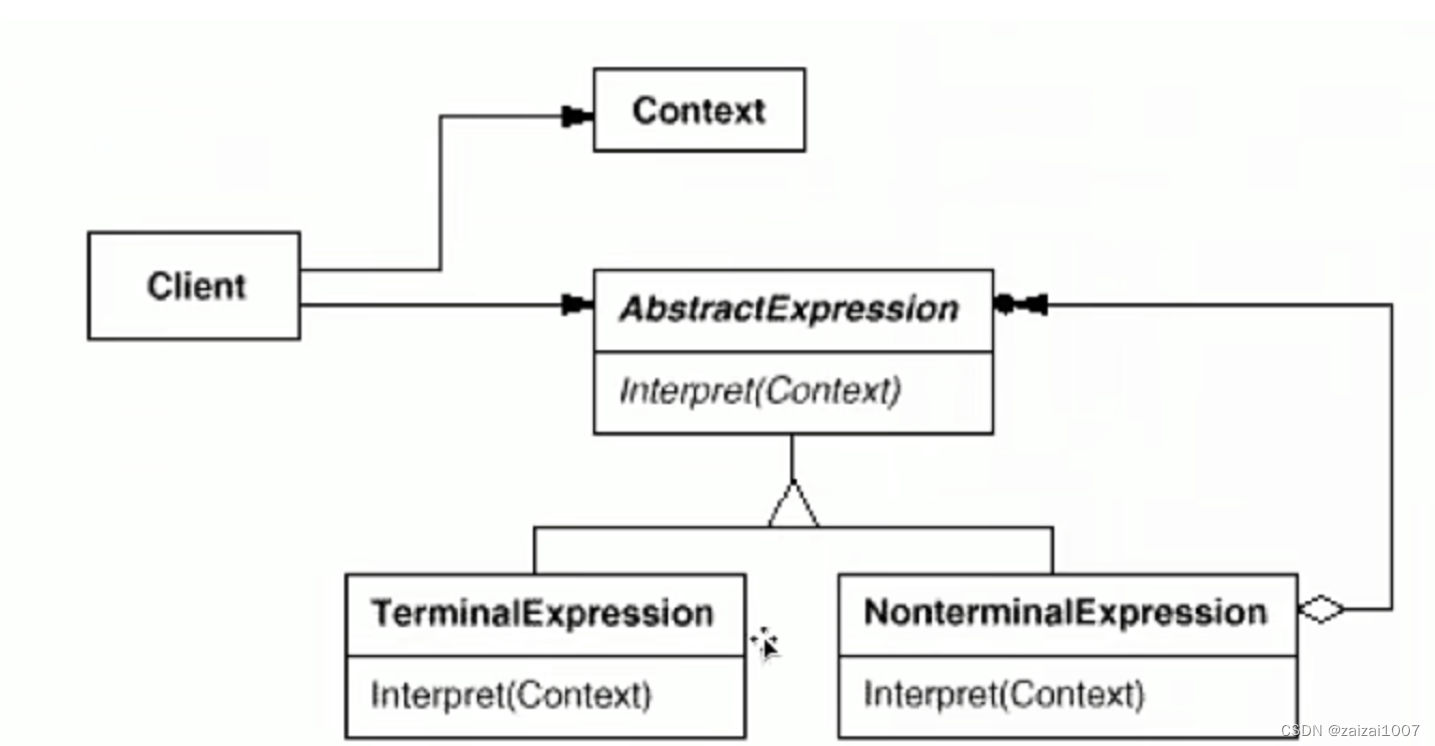
设计模式学习2
代理模式:Proxy 动机 “增加一层间接层”是软件系统中对许多复杂问题的一种常见解决方案。在面向对象系统中,直接食用某些对象会带来很多问题,作为间接层的proxy对象便是解决这一问题的常见手段。 2.伪代码: class ISubject{ pu…...

Rust:如何判断位置结构的JSON串的成员的数据类型
如何判断位置结构的JSON串的成员的数据类型,给一个Rust的例子,其中包含对数组的判断? 在Rust中,你可以使用serde_json库来处理JSON数据,并通过serde_json::Value类型的方法来判断JSON串中成员的数据类型。以下是一个示…...
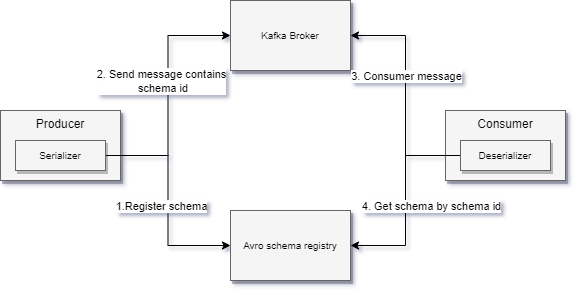
Kafka(五)生产者
目录 Kafka生产者1 配置生产者bootstrap.serverskey.serializervalue.serializerclient.id""acksallbuffer.memory33554432(32MB)compression.typenonebatch.size16384(16KB)max.in.flight.requests.per.connection5max.request.size1048576(1MB)receive.buffer.byte…...

【Leetcode】242.有效的字母异位词
一、题目 1、题目描述 给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。 注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。 示例1: 输入: s = "anagram", t = "nagaram" 输出: true示例2: 输入: …...
关系数据理论的函数依赖)
【数据库原理】(16)关系数据理论的函数依赖
一.函数依赖的概念 函数依赖是关系数据库中核心的概念,它指的是在属性集之间存在的一种特定的关系。这种关系表明,一个属性集的值可以唯一确定另一个属性集的值。 属性子集:在关系模式中,X和Y可以是单个属性,也可以是…...

脆弱的SSL加密算法漏洞原理以及修复方法
漏洞名称:弱加密算法、脆弱的加密算法、脆弱的SSL加密算法、openssl的FREAK Attack漏洞 漏洞描述:脆弱的SSL加密算法,是一种常见的漏洞,且至今仍有大量软件支持低强度的加密协议,包括部分版本的openssl。其实…...
)
SVN迁移至GitLab,并附带历史提交记录(二)
与《SVN迁移至GitLab,并附带历史提交记录》用的 git svn clone不同,本文使用svn2git来迁移项目代码。 一、准备工作 安装Git环境,配置本地git账户信息: git config --global user.name "XXX" git config --global us…...
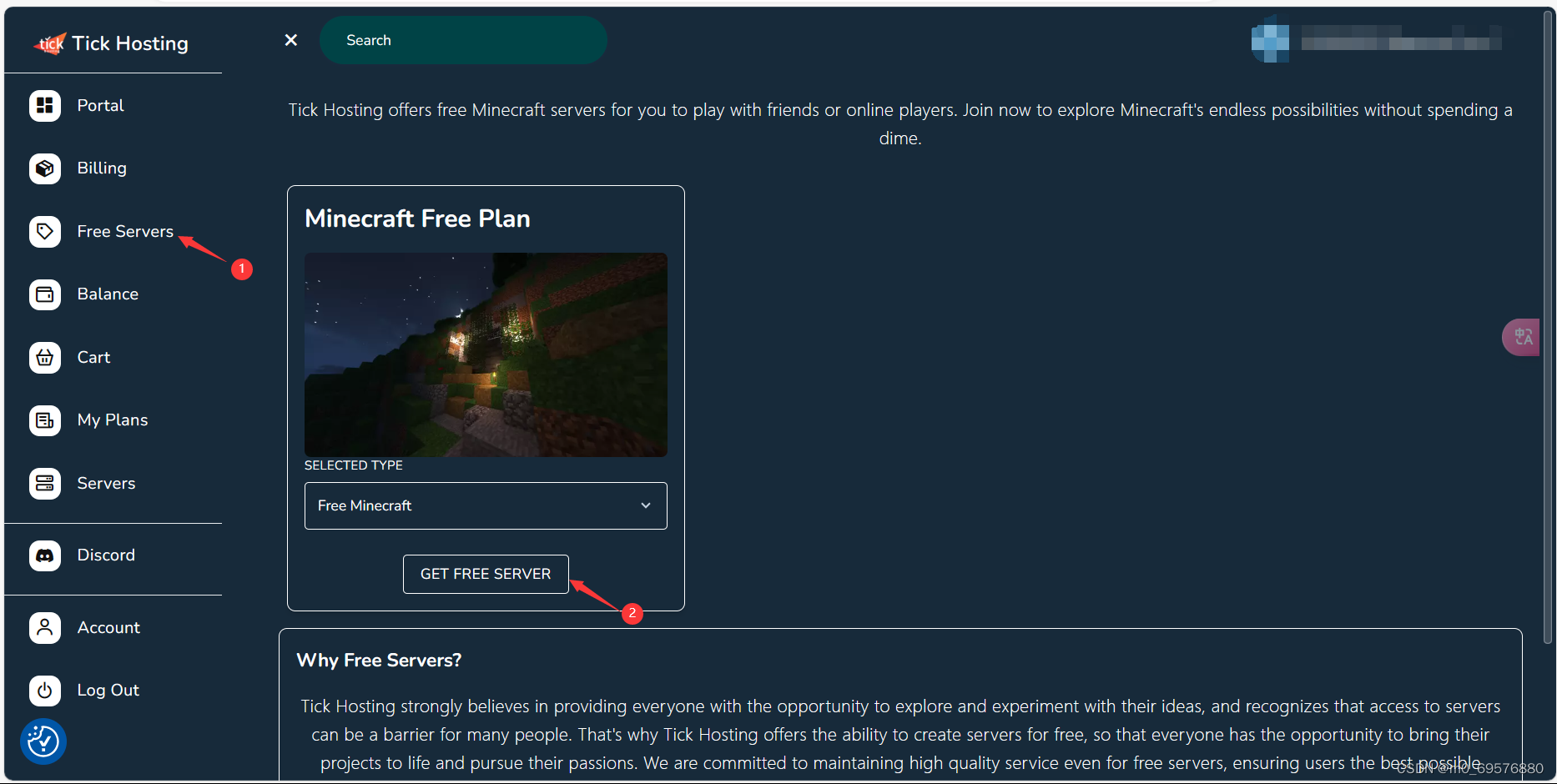
如何创建容器搭建节点
1.注册Discord账号 https://discord.com/这是登录网址: https://discord.com/ 2.点击startnow注册,用discord注册或者邮箱注册都可,然后登录tickhosting Tick Hosting这是登录网址:Tick Hosting 3.创建servers 4.点击你创建的servers,按照图中步骤进行...

微众区块链观察节点的架构和原理 | 科普时间
践行区块链公共精神,实现更好的公众开放与监督!2023年12月,微众区块链观察节点正式面向公众开放接入功能。从开放日起,陆续有多个观察节点在各地运行,同步区块链数据,运行区块链浏览器观察检视数据…...
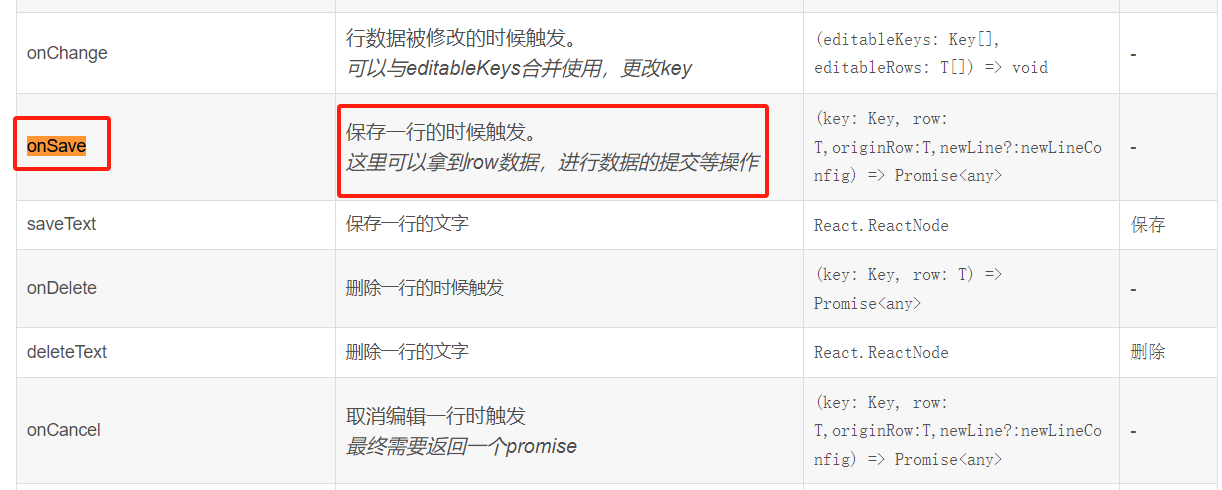
React Admin 前端脚手架之ant-design-pro
文章目录 一、React Admin 前端脚手架选型二、React Admin 前端脚手架之ant-design-pro三、ant-design-pro使用步骤四、调试主题五、常用总结(持续更新)EditableProTable组件 常用组件EditableProTable组件 编辑某行后,保存时候触发发送请求EditableProTable组件,添加记录提…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
