可碧教你C++——位图

本章节是哈希的延申

可碧教你C++——哈希
http://t.csdnimg.cn/3R8TU
一文详解C++——哈希
位图
位图是基于哈希表的原理产生的一种新的container——bitset
 基于哈希映射的原理,我们在查找的时候,可以直接去定址到元素的具体位置,然后直接访问该元素。但是如果没有哈希冲突,我们甚至完全不需要检查哈希映射对应的元素是否为我们需要查找的元素,直接判断这个位置有没有元素,便可以知道该元素在不在哈希表里。
基于哈希映射的原理,我们在查找的时候,可以直接去定址到元素的具体位置,然后直接访问该元素。但是如果没有哈希冲突,我们甚至完全不需要检查哈希映射对应的元素是否为我们需要查找的元素,直接判断这个位置有没有元素,便可以知道该元素在不在哈希表里。
 而判断某一个位置有没有元素,只需要0和1便可以完成,也就是无论被存储数据的大小,每个数据只需要1个比特位的存储空间,这无疑极大压缩了内存空间。而通过这种方式实现的数据结构,便被称为——位图。
而判断某一个位置有没有元素,只需要0和1便可以完成,也就是无论被存储数据的大小,每个数据只需要1个比特位的存储空间,这无疑极大压缩了内存空间。而通过这种方式实现的数据结构,便被称为——位图。
位图的结构
一般来说,我们只有在内存空间不足以解决既有的问题下,才会去考虑缩小数据空间的问题。同样,内存的使用场景一般是在有着海量数据下,我们要对某个数据进行查重,才会使用位图。位图的原理是哈希表,其构成当然离不开数组,实际上位图和普通的哈希表构成几乎相同, 只不过将数组的单元格变成了一个个的比特位。
但是,C++中并无法将单个比特位作为单元格,我们只能通过某种方法间接去访问比特位
例如:我们将每个单元格设为整型int,然后每个整型int具有4字节32个比特位,我们便可以通过相除的方式寻找具体的单元格,再用除余的方式寻找比特位.
 这便是位图的最基本的结构:
这便是位图的最基本的结构:
class bitset
{private:vector<int> _table;//可以是任何模板参数,只需要该参数所占有的比特位//但是最好不要用指针,因为在不同位的电脑上指针的比特位不同
}位图的访问
位图的访问实际上是对比特位的访问。但是我们很难专门去访问某一个比特位,我们只能采取异或的方法,将其他位全置为0,从而间接访问具体的一位的值。

通过以上两个式子,我们很快就能找到解决方案:
 只要构建出一个辅助量,其他位都为0,只有被查找的那一位为1,然后取&,最终得到的结果便只与需要查找的值有关了。如果该值为1,则整个值非0,返回true;如果该值为0,则整个值为0,返回false。
只要构建出一个辅助量,其他位都为0,只有被查找的那一位为1,然后取&,最终得到的结果便只与需要查找的值有关了。如果该值为1,则整个值非0,返回true;如果该值为0,则整个值为0,返回false。
下一个问题便是,如何构建这一个辅助量?这便需要用到移位运算符。
 也就是说,我们想访问哪一位,就只需要移位多少位,便可以达成条件。
也就是说,我们想访问哪一位,就只需要移位多少位,便可以达成条件。
//查找元素,约等于find
bool test(int key)
{size_t plane = key / 32;//第几辆飞机size_t seat = key % 32;//第几个座位return _table[plane] & (1 << seat);//构建辅助量并&
}位图的插入和删除
位图的插入和删除,实际上也是考虑如何在不影响其他比特位的情况下,对某一具体比特位的操作。
插入,就是将该位便为1;删除,就是将该位便为0,这里又需要我们使用异或的性质:

于是很容易想到
- 插入的时候,我们使用|,辅助量为其他位全为0,修改位为1
- 删除的时候,我们使用&,辅助量其他位全为1,修改位为0
位图的实现
位图不支持扩容。我们在使用位图的时候,就必须传入位图需要的空间大小
class bitset
{
public:bitset(int n){_table.resize(n);}//将元素设为1,约等于insertvoid set(int key){size_t plane = key / 32;size_t seat = key % 32;_table[plane] |= (1 << seat);}//将元素设为0,约等于erasevoid reset(int key){size_t plane = key / 32;size_t seat = key % 32;_table[plane] &= ~(1 << seat);}//查找元素,约等于findbool test(int key){size_t plane = key / 32;size_t seat = key % 32;return _table[plane] & (1 << seat);}
private:vector<int> _table;
};布隆过滤器
上面所述的位图都是在不考虑哈希冲突的情况下所实现,但是实际上,哈希冲突是不可能被避免的。 难道必须要在规定没有哈希冲突的情况下,位图才有意义吗?当然不是。我们不妨直面哈希冲突,看看在有哈希冲突的情况下,位图会产生什么影响。
哈希冲突会导致其他与其具有相同哈希映射值的元素,也被视作为存在于哈希表中。
- 如果数据存在,无论该位是否存在冲突,则该位一定为1;
- 如果数据不存在,则该为可能为0,也可能会因其他数据的冲突导致该位为1;
而反过来通过表中的状态判断数据是否存在于表中
- 如果表中存在,无法判断该数据是否存在,因为可能是其他的值产生的1
- 如果表中不存在,则该哈希映射值对应的所有元素一定都不存在
是不是就像大家平时上课签到一样
 也就是说,我们可以采用他的准确性——判断数据是否不在表中
也就是说,我们可以采用他的准确性——判断数据是否不在表中
最常见的应用场景便是取名查重。我们可以接受一个未被取的名字被视为已经占用,但是不能接收重名,此时采用这种过滤方式,可以在满足条件的情况下尽可能节省空间。
多重过滤
尽管我们可以接受误判,但是我们还是不想有太多类似于科比布莱恩特24这样因误判而导致可取名变少带来的产物,那还有没有其他办法去尽量避免呢?
既然一重过滤会导致误判,那多重过滤,是不是误判就减少了

- 只有三个毕业证都存在,才表示学历是真真正正存在的。
- 而如果其中任何一个毕业证不存在,则表示其学历是伪造的。
我们创建三个位图,每个位图使用不同的哈希映射,当一个数据插入到布隆过滤器时,会映射到三个不同的位置上,每个位图都会产生相应的插入结果。也就是说,只有当三个位图都存在该数据,才表示布隆过滤器存在该数据。 相应的,如果任何一个位图中不存在某个数据,则表示其他位图中该数据的存在时哈希冲突产生的。而因为采用了多种哈希映射,三个位图的哈希冲突完全相同的可能性几乎为0,也就避免了哈希冲突的存在。
class bloom_filter
{private:bitset _hash1;bitset _hash2;bitset _hash3;
}布隆过滤器的问题
虽然布隆过滤器可以避免插入的哈希冲突,但是还是有这样一个巨大的问题——删除。
我们想删除一个数据,当然是将三个位图中所有对应的数据都删除。但是删除以后,哈希冲突导致的其他数据也被删除了。这种改变是不可逆的,因为我们并不知道到底有多少数据在该位上哈希冲突了。等到判断的时候,因为该数据在某一个表中被误删,导致就算该数据在其他两个表中仍存在,也会被误判为不存在。
所以,布隆过滤器一般是不允许删除的,当然也有解决方法,便是在每个位置上进行引用计数,但是这便舍弃了布隆过滤器节省空间的初衷和优点。
哈希切割
哈希切割不是一个具体的container。哈希切割是利用哈希的思想,对某些问题处理的方法。
假如某个数据库存有海量的数据,一个服务器并没有办法很好处理这些数据,要将这些数据分开到几个不同的服务器进行处理,往往会面临几个需求
- 相同或类似的数据放在同一个服务器中
- 每一个服务器的数据量尽量平均
- 尽量不要浪费空间以减少服务器的数量

此时红黑树等容器便没有办法满足了。尽管一些有序容器可以处理数据的特征,但是因为服务器的分离,红黑树很难去跨设备访问其他数据,所以这里大部分container都会罢工。
在这里,我们就必须采取哈希的思想,通过数据的除余,将除余相同的数据放在同一个服务器中。这样,重复的数据自然因除余相同被归类到了一个服务器里,而类似的数据同样可以通过一些算法分割到相同的服务器中。

相关文章:

可碧教你C++——位图
本章节是哈希的延申 可碧教你C——哈希http://t.csdnimg.cn/3R8TU 一文详解C——哈希 位图 位图是基于哈希表的原理产生的一种新的container——bitset 基于哈希映射的原理,我们在查找的时候,可以直接去定址到元素的具体位置,然后直接访问该…...

2024年虚拟DOM技术将何去何从?
从诞生之初谈起,从命令式到声明式,Web开发的演变之路 Web开发的起源与jQuery的统治 在Web开发的早期阶段,操作DOM元素主要依赖命令式编程。当时,jQuery因其易用性而广受欢迎。使用jQuery,开发者通过具体的命令操作DOM&…...

基于51单片机的恒温淋浴器控制电路设计
标题:基于51单片机的智能恒温淋浴器控制系统设计与实现 摘要: 本论文主要探讨了一种基于STC89C51单片机为核心控制器的恒温淋浴器控制系统的详细设计与实现。系统通过集成温度传感器实时监测水温,结合PID算法精确控制加热元件工作状态&#…...

【redis】redis的bind配置
在配置文件redis.conf中,默认的bind 接口是127.0.0.1,也就是本地回环地址。这样的话,访问redis服务只能通过本机的客户端连接,而无法通过远程连接, 这样可以避免将redis服务暴露于危险的网络环境中,防止一些…...
C++ 继承
目录 一、继承的概念及定义 1、继承的概念 2、继承定义 二、基类和派生类对象赋值转换 三、继承中的作用域 四、派生类的默认成员函数 五、继承与友元 六、继承与静态成员 七、复杂的菱形继承及菱形虚拟继承 1、菱形继承 2、虚拟继承 3、例题 八、继承的总结和反思…...

了解ASP.NET Core 中的文件提供程序
写在前面 ASP.NET Core 通过文件提供程序来抽象化文件系统访问。分为物理文件提供程序(PhysicalFileProvider)和清单嵌入的文件提供程序(ManifestEmbeddedFileProvider)还有复合文件提供程序(CompositeFileProvider );其中PhysicalFileProvider 提供对物理文件系统…...
竞赛保研 基于深度学习的人脸性别年龄识别 - 图像识别 opencv
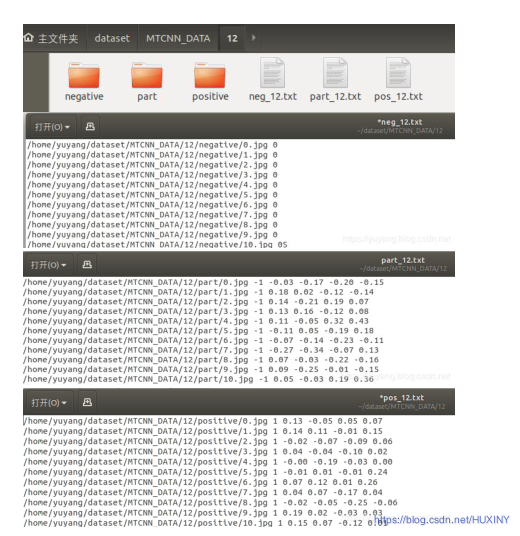
文章目录 0 前言1 课题描述2 实现效果3 算法实现原理3.1 数据集3.2 深度学习识别算法3.3 特征提取主干网络3.4 总体实现流程 4 具体实现4.1 预训练数据格式4.2 部分实现代码 5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 毕业设计…...

JavaScript音视频,JavaScript简单获取电脑摄像头画面并播放
前言 本章实现JavaScript简单获取电脑摄像头画面并播放的功能 兼容性(不支持Node.js) 需要注意的是,由于涉及到用户的隐私和安全,获取用户媒体设备需要用户的明确同意,并且可能需要在用户的浏览器中启用相关的权限。在某些浏览器中,可能需要用户手动开启摄像头权限。 …...

《JVM由浅入深学习【五】 2024-01-08》JVM由简入深学习提升分享
目录 JVM何时会发生堆内存溢出?1. 堆内存溢出的定义2. 内存泄漏的原因3. 堆内存溢出的常见场景4. JVM参数调优5. 实际案例分析 JVM如何判断对象可以回收1.可达性分析的基本思路2.实际案例3.可以被回收的对象4.拓展, 谈谈 Java 中不同的引用类型? 结语感…...
FastDFS之快速入门、上手
知识概念 分布式文件系统 通过计算机网络将各个物理存储资源连接起来。通过分布式文件系统,将网络上任意资源以逻辑上的树形结构展现,让用户访问网络上的共享文件更见简便。 文件存储的变迁: 直连存储:直接连接与存储…...

Vue 中的 ref 与 reactive:让你的应用更具响应性(中)
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...
【数据库基础】Mysql与Redis的区别
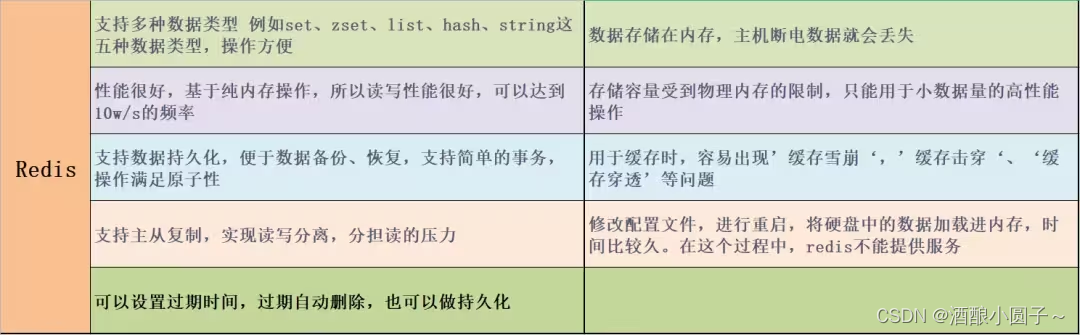
看到一篇不错的关于“Mysql与Redis的区别”的文章,转过来记录下~ 文章目录 一、数据库类型二、运行机制三、什么是缓存数据库呢?四、优缺点比较五、区别总结六、数据可以全部直接用Redis储存吗?参考资料 一、数据库类型 Redis:NOS…...

JVM工作原理与实战(六):类的生命周期-连接阶段
专栏导航 JVM工作原理与实战 RabbitMQ入门指南 从零开始了解大数据 目录 专栏导航 前言 一、类的生命周期 1.加载(Loading) 2.连接(Linking) 3.初始化(Initialization) 4.使用(Using&…...

【OCR】 - Tesseract OCR在Windows系统中安装
Tesseract OCR 在Windows环境下安装Tesseract OCR(Optical Character Recognition)通常包括以下几个步骤: 下载Tesseract 访问Tesseract的GitHub发布页面:https://github.com/tesseract-ocr/tesseract/releases找到适合你操作系…...

YOLOv8改进 | 损失函数篇 | SlideLoss、FocalLoss分类损失函数助力细节涨点(全网最全)
一、本文介绍 本文给大家带来的是分类损失 SlideLoss、VFLoss、FocalLoss损失函数,我们之前看那的那些IoU都是边界框回归损失,和本文的修改内容并不冲突,所以大家可以知道损失函数分为两种一种是分类损失另一种是边界框回归损失,上一篇文章里面我们总结了过去百分之九十的…...
)
计算机网络试题——填空题(附答案)
在OSI模型中,第一层是____________层。 答案:物理(Physical) TCP协议是一种_____________连接的协议。 答案:面向连接(Connection-oriented) IPv6地址的位数是____________。 答案:1…...

第二证券:股票私募仓位指数创近八周新高
1月8日,A股几大首要指数全线收跌,上证指数收于日内最低点2887.54点,间隔上一年5月份的阶段高点3418.95点现已跌去了15.54%。 不过,虽然商场仍未清晰止跌,私募基金们却现已进场“抄底”。私募排排网最新发布的私募仓位…...

35-javascript基础,引入方式;变量命名规范
html分为三部分;结构html,表现css,行为js;js就是javascript js包含三部分: ECMAScript:简称ES,ES5,ES6核心语法 DOM:获取和操作html元素的标准方法;BOM&am…...

笔试案例2
文章目录 1、笔试案例22、思维导图 1、笔试案例2 09)查询学过「张三」老师授课的同学的信息 selects.*,c.cname,t.tname,sc.score from t_mysql_teacher t, t_mysql_course c, t_mysql_student s, t_mysql_score sc where t.tidc.cid and c.cidsc.cid and sc.sids…...

【嵌入式-网络编程】vmware中使用UDP广播失败问题
问题描述: 自己在vmware中搭建了2台虚拟机,虚拟机A向虚拟机A和虚拟机B发送广播信息,接收端在虚拟机A和虚拟机B,这个时候,由于没配置sin.sin_addr.s_addr htonl(INADDR_ANY);,而是配置的inet_pton(AF_INET,…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

