当前位置： 首页 > news >正文

w20webshell之文件上传

news 2026/2/8 22:35:01
  • 1.什么是文件上传？
    将本地文件传输到指定位置。
  • 2.什么是webshell
    给恶意脚本提供运行环境
  • 3.文件上传所需要的条件
    a.文件成功上传，未被删除
    b.知道文件路径
    c.文件所在系统支持脚本运行
  • 4.文件上传流程
    支持任意文件上传的文件上传
    a.恶意文件上传成功
    b.根据服务器返回的文件路径，进行访问
    c.根据访问结果判断文件所在系统是否支持脚本运行。
    限制文件类型的文件上传（可绕过客户端的情况）
    a.开启burpsuite工具和浏览器代理插件，进行抓包
    b.将伪装的恶意文件，进行后缀名修改回来
    c.对Content-Type进行修改。
    d.恶意文件上传成功
    e.根据服务器返回的文件路径，进行访问
    i.根据访问结果判断文件所在系统是否支持脚本运行。
  • 5.webshell有哪些
    菜刀、蚁剑、冰蝎

熟悉各个webshell管理工具

相关文章：

w20webshell之文件上传

1.什么是文件上传？ 将本地文件传输到指定位置。2.什么是webshell 给恶意脚本提供运行环境3.文件上传所需要的条件 a.文件成功上传，未被删除 b.知道文件路径 c.文件所在系统支持脚本运行4.文件上传流程 支持任意文件上传的文件上传 a.恶意文件上传成功 b.…...

编程日记 2024/1/10 2:54:46

【Redis】非关系型数据库之Redis的主从复制、哨兵和集群高可用

目录 一、主从复制、哨兵、集群的区别 二、主从复制 2.1主从复制的作用 2.2主从复制的原理 2.3主从复制的实操 步骤一：环境准备 步骤二：安装Redis以及配置文件修改 Redis的主从配置文件都一样 步骤四：验证主从复制 三、哨兵 3.1哨兵…...

编程日记 2024/1/10 2:53:46

从私有Git仓库的搭建到命令的使用及部署再到分支管理

一、版本控制系统/版本控制器 1. 版本控制系统： git 分布式 —没有中心代码库，所有机器之间的地位同等（每台机器上都有相同的代码） svn 集中管理的 —有中心代码库，其他都是客户端 2.git与svn介绍 1.git属于分布…...

编程日记 2024/1/10 2:48:41

mysql基础-常用函数汇总

目录 1. 查询技巧 2. 时间函数 2.1 now() 2.2 current_date() 2.3 时间差timestampdiff（）与datediff（） 2.4 其他时间函数 3. 字符函数 3.1 截取函数 3.2 分割函数 3.3 left与right函数 3.4 其他函数 4. 数字函数 5. …...

编程日记 2024/1/10 2:46:38

COCO数据格式的json文件内容

COCO（Common Objects in Context）数据集现在有3种标注类型：object instances（目标实例）, object keypoints（目标上的关键点）, 和image captions（看图说话），使用JSON文件存储，包含了对图像中目标的边界框、类别标签、分割掩码等信息。 COCO标注文件是一个包含多个字…...

编程日记 2024/1/10 2:45:37

AI-数学-高中-3.二次函数的根的分布问题的解题方法

原作者学习视频：二次】3二次函数根分布问题（中档）_哔哩哔哩_bilibili 一、伟达定理（根与0比较的二次函数） 示例： 二、画图法： 1.开口方向的确定，有的示例可能存在向上、下两种情况…...

编程日记 2024/1/10 2:44:36

golang中gorm使用

前言 记录下go语言操作mysql数据库，选用gorm，gorm是一个流行的对象关系映射（ORM）库，用于简化与数据库的交互。 接入步骤 安装gorm：首先，你需要使用Go模块来安装gorm。在终端中运行以下命令&…...

编程日记 2024/1/10 2:43:35

centoss7安装mysql详细教程

【MySQL系列】在Centos7环境安装MySQL_centos7安装mysql-CSDN博客 【MySQL系列】在Centos7环境安装MySQL_centos7安装mysql-CSDN博客 【MySQL系列】在Centos7环境安装MySQL_centos7安装mysql-CSDN博客...

编程日记 2024/1/10 2:42:34

SpringBoot-拓展

邮件 依赖 <groupId>org.springframework.boot</groupId> <artifactId>spring-boot-starter-mail</artifactId>配置 spring.mail.username邮箱 spring.mail.password授权码 spring.mail.hostsmtp.qq.com # 开启加密验证 spring.mail.properties.mai…...

编程日记 2024/1/10 2:40:31

用于查询性能预测的计划结构深度神经网络模型--大数据计算基础大作业

用于查询性能预测的计划结构深度神经网络模型 论文阅读和复现 24.【X1.1】 在关系数据库查询优化领域&#xff0c;对查询时间的估计准确性直接决定了查询优化结果&#xff0c;进而影响到数据库整体的查询效率。但由于数据库自身的复杂性&#xff0c;查询时间受到数据分布、数据…...

编程日记 2024/1/10 2:38:28

MySQL5.7用于控制副本服务器的 SQL 语句

官网地址&#xff1a;MySQL :: MySQL 5.7 Reference Manual :: 13.4.2 SQL Statements for Controlling Replica Servers 欢迎关注留言&#xff0c;我是收集整理小能手&#xff0c;工具翻译&#xff0c;仅供参考&#xff0c;笔芯笔芯. MySQL 5.7 参考手册 / ... / CHANGE M…...

编程日记 2024/1/10 2:37:28

stable diffusion 人物高级提示词（四）朝向、画面范围、远近、焦距、机位、拍摄角度

一、朝向 英文中文front view正面Profile view / from side侧面half-front view半正面Back view背面(quarter front view:1.5)四分之一正面 prompt/英文中文翻译looking at the camera看向镜头facing the camera面对镜头turned towards the camera转向镜头looking away from …...

编程日记 2024/1/10 2:36:27

C#.Net学习笔记——设计模式六大原则

***************基础介绍*************** 1、单一职责原则 2、里氏替换原则 3、依赖倒置原则 4、接口隔离原则 5、迪米特法原则 6、开闭原则 一、单一职责原则 举例&#xff1a;类T负责两个不同的职责&#xff1a;职责P1&#xff0c;职责P2。当由于职责P1需求发生改变而需要修…...

编程日记 2024/1/10 2:29:19

go 修改postgresql的配置参数

postgresql.conf与postgresql.auto.conf的区别 postgresql.auto.conf的优先级高于postgresql.conf&#xff0c;如果一个参数同时存在postgresql.auto.conf和postgresql.conf里面&#xff0c;系统会先读postgresql.auto.conf的参数配置。 使用alter system set修改的是postgres…...

编程日记 2024/1/10 2:28:18

解决word图片格式错乱、回车图片不跟着换行的问题

解决word图片格式错乱、回车图片不跟着换行的问题 1.解决方法。 先设置为嵌入型 但是设置的话会出现下面的问题。图片显示不全。 进一步设置对应的行间距&#xff0c;原先设置的是固定值&#xff0c;需要改为1.5倍行距的形式&#xff0c;也就是说不能设置成固定值就可以。...

编程日记 2024/1/10 2:27:17

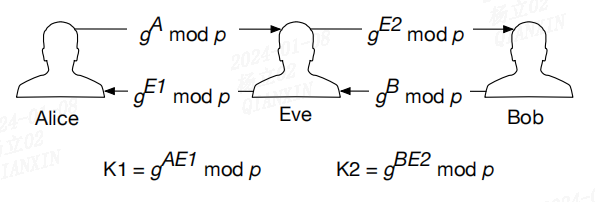
密码学（二）

文章目录 前言一、Certificate Authorities二、Key Agreement Protocols 前言 本文来自 Intel SGX Explained 请参考&#xff1a;密码学&#xff08;一&#xff09; 一、Certificate Authorities 非对称密钥密码学中的公钥和私钥假设每个参与方都拥有其他参与方的正确公钥。…...

编程日记 2024/1/10 2:26:16

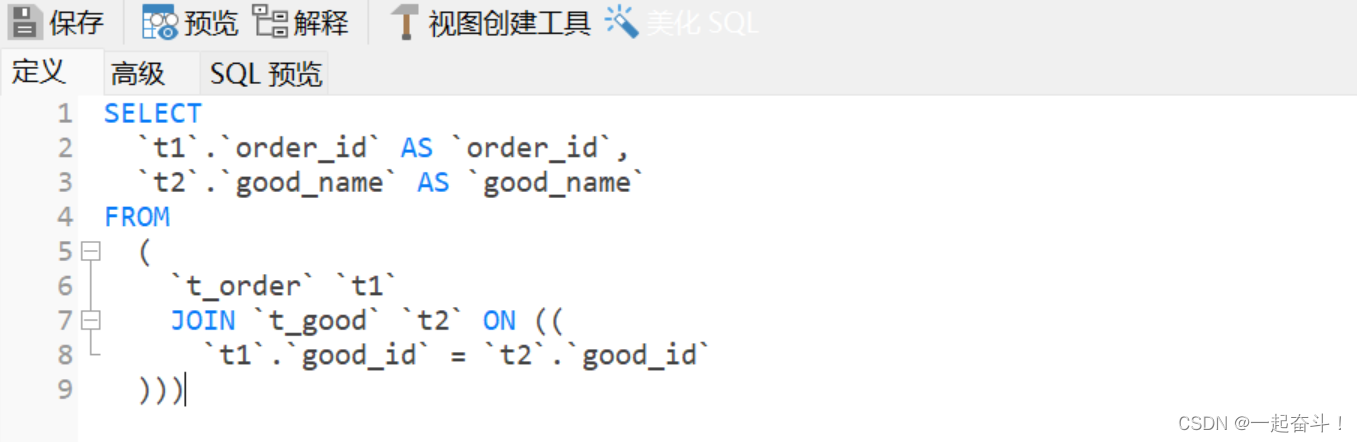
mysql进阶-视图

目录 1. 用途 2. 语法 2.1 创建或替换视图 2.2 修改视图 2.3 查看视图&#xff1a; 2.4 删除视图&#xff1a; 3. 其他 3.1 操作视图 3.2 迁移数据库 1. 用途 视图可以理解为一个复杂查询的简称&#xff0c;它可以帮助我们简化查询&#xff0c;主要用于报表查询:例如…...

编程日记 2024/1/10 2:24:15

力扣-34. 在排序数组中查找元素的第一个和最后一个位置

文章目录 力扣题目代码 力扣题目 给你一个按照非递减顺序排列的整数数组 nums&#xff0c;和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target&#xff0c;返回 [-1, -1]。 你必须设计并实现时间复杂度为 O(log n) 的算…...

编程日记 2024/1/10 2:23:14

Cesium笔记 初始化 使用Vue-Cesium 组件

参考 A Vue 3 based component library of CesiumJS for developers | Vue for CesiumVue for Cesium, a Vue 3.x based component library of CesiumJS for GISerhttps://zouyaoji.top/vue-cesium/#/zh-CN/component/quickstart...

编程日记 2024/1/10 2:20:11

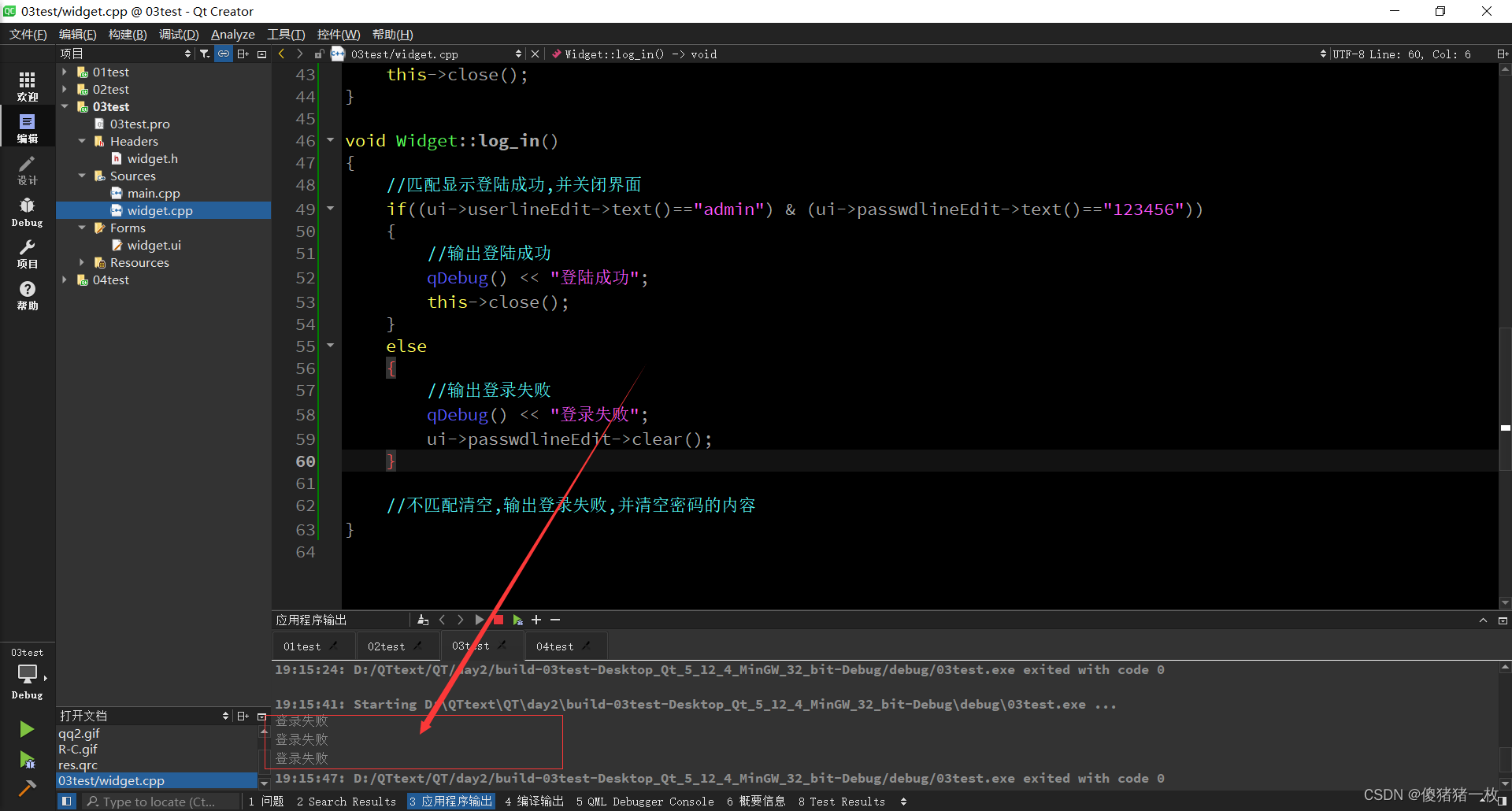
QTday2作业

思维导图: 使用手动连接&#xff0c;将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中&#xff0c;在自定义的槽函数中调用关闭函数; 将登录按钮使用qt5版本的连接到自定义的槽函数中&#xff0c;在槽函数中判断u界面上输入的账号是否为"admin"&#xff0c…...

编程日记 2024/1/10 2:18:10

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中，手势开发全攻略：

在 HarmonyOS 应用开发中&#xff0c;手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力&#xff0c;既支持点击、长按、拖拽等基础单一手势的精细控制&#xff0c;也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档&#xff0c…...

编程新知 2025/9/19 4:31:58

《基于Apache Flink的流处理》笔记

思维导图 1-3 章 4-7章 8-11 章 参考资料 源码&#xff1a; https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

编程新知 2026/1/31 14:55:53

MySQL中【正则表达式】用法

MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现&#xff08;两者等价&#xff09;&#xff0c;用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例&#xff1a; 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

编程新知 2025/11/21 22:02:37

Linux离线（zip方式）安装docker

目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1&#xff1a;修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本&#xff1a;CentOS 7 64位 内核版本&#xff1a;3.10.0 相关命令&#xff1a; uname -rcat /etc/os-rele…...

编程新知 2025/11/23 23:50:53

Mysql8 忘记密码重置，以及问题解决

1.使用免密登录 找到配置MySQL文件&#xff0c;我的文件路径是/etc/mysql/my.cnf&#xff0c;有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

编程新知 2026/1/9 8:59:09

push [特殊字符] present

push &#x1f19a; present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中&#xff0c;push 和 present 是两种不同的视图控制器切换方式&#xff0c;它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

编程新知 2026/1/31 4:26:17

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

Python+ZeroMQ实战：智能车辆状态监控与模拟模式自动切换

目录 关键点 技术实现1 技术实现2 摘要&#xff1a; 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式&#xff08;自动驾驶、人工驾驶、远程驾驶、主动安全&#xff09;&#xff0c;并通过实时消息推送更新车…...

编程新知 2025/11/12 0:06:50

MinIO Docker 部署：仅开放一个端口

MinIO Docker 部署：仅开放一个端口 在实际的服务器部署中，出于安全和管理的考虑，我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务，支持 Docker 部署，但默认情况下它需要两个端口：一个是 API 端口（用于存储和访问数据），另一个是控制台端口（用于管理界面…...

编程新知 2025/12/23 11:08:56

华为OD机试-最短木板长度-二分法(A卷,100分)

此题是一个最大化最小值的典型例题&#xff0c; 因为搜索范围是有界的&#xff0c;上界最大木板长度补充的全部木料长度&#xff0c;下界最小木板长度&#xff1b; 即left0,right10^6; 我们可以设置一个候选值x(mid)&#xff0c;将木板的长度全部都补充到x&#xff0c;如果成功…...

编程新知 2026/2/4 17:42:50