python实现PCA降维画分类散点图并标出95%的置信区间
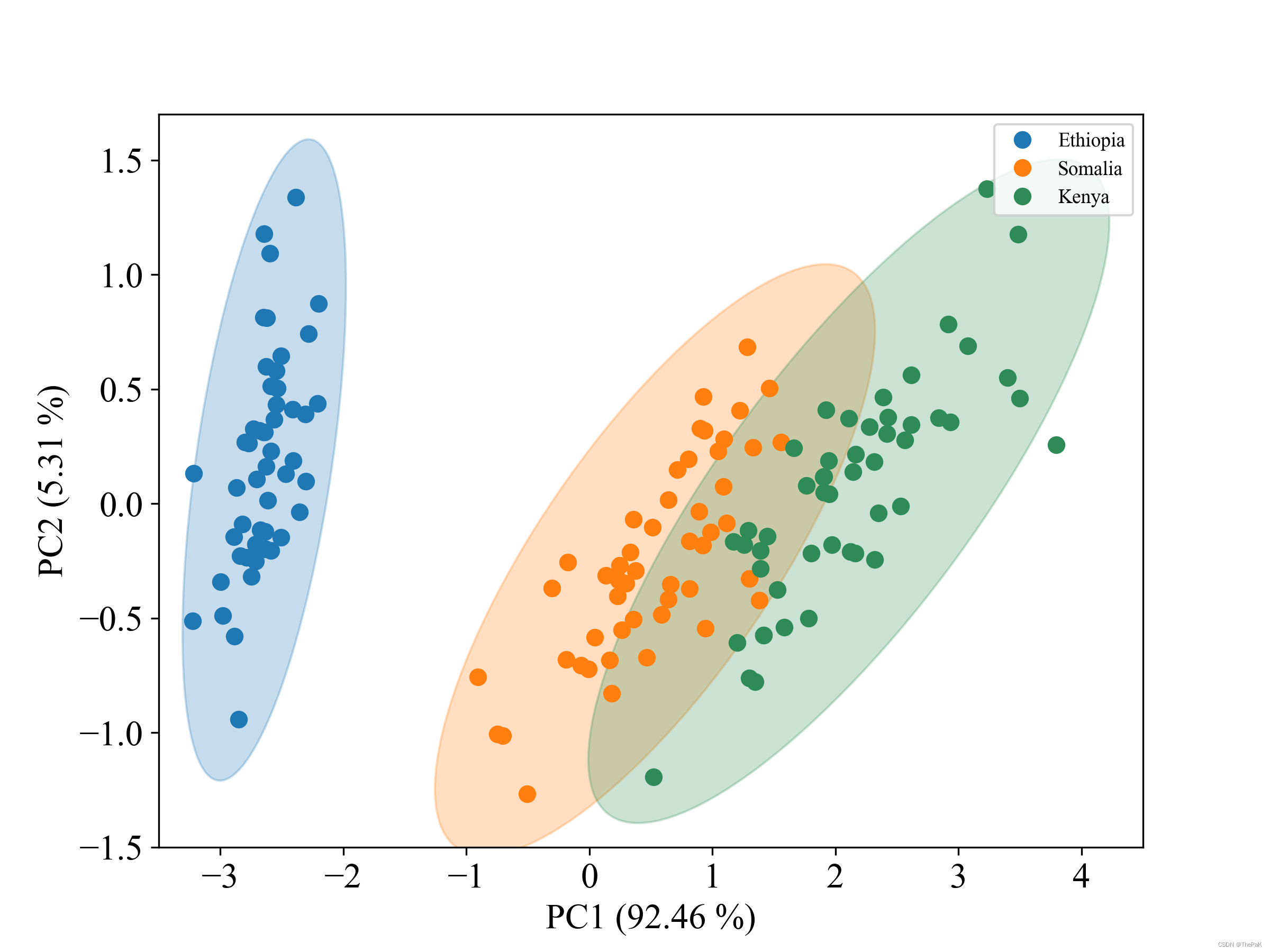
此代码以数据集鸢尾花为例,对其使用PCA降维后,绘制了三个类别的样本点和对应的置信圆(即椭圆)。先放效果图。
下面是完整代码:
from matplotlib.patches import Ellipsedef plot_point_cov(points, nstd=3, ax=None, **kwargs):# 求所有点的均值作为置信圆的圆心pos = points.mean(axis=0)# 求协方差cov = np.cov(points, rowvar=False)return plot_cov_ellipse(cov, pos, nstd, ax, **kwargs)def plot_cov_ellipse(cov, pos, nstd=3, ax=None, **kwargs):def eigsorted(cov):cov = np.array(cov)vals, vecs = np.linalg.eigh(cov)order = vals.argsort()[::-1]return vals[order], vecs[:, order]if ax is None:ax = plt.gca()vals, vecs = eigsorted(cov)theta = np.degrees(np.arctan2(*vecs[:, 0][::-1]))width, height = 2 * nstd * np.sqrt(vals)ellip = Ellipse(xy=pos, width=width, height=height, angle=theta, **kwargs)ax.add_artist(ellip)return ellip'''画置信圆'''
def show_ellipse(X_pca, y, pca, flag=1):# 定义颜色colors = ['tab:blue', 'tab:orange', 'seagreen']regions = ['Ethiopia', 'Somalia', 'Kenya']# 定义分辨率plt.figure(dpi=300, figsize=(8, 6))# 三分类则为3for i in range(0, 3):pts = X_pca[y == int(i), :]new_x, new_y = X_pca[y==i, 0], X_pca[y==i, 1]plt.plot(new_x, new_y, '.', color=colors[i], label=regions[i], markersize=14)plot_point_cov(pts, nstd=3, alpha=0.25, color=colors[i])# 添加坐标轴plt.xlim(-3.5, 4.5)plt.ylim(-1.5, 1.7)plt.xticks(size=16, family='Times New Roman')plt.yticks(size=16, family='Times New Roman')font = {'family': 'Times New Roman', 'size': 16}plt.xlabel('PC1 ({} %)'.format(round(pca.explained_variance_ratio_[0] * 100, 2)), font)plt.ylabel('PC2 ({} %)'.format(round(pca.explained_variance_ratio_[1] * 100, 2)), font)plt.legend(prop={"family": "Times New Roman", "size": 9}, loc='upper right')plt.show()import pandas as pd
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
labels = ['setosa', 'versicolor', 'virginica']
iris = load_iris()
X = iris.data
y = iris.target_names[iris.target]print("y length--------", len(y))
y_category = pd.Categorical(y,ordered=True,categories=['setosa', 'versicolor', 'virginica'])y = y_category.codes
print(y)
print(y.shape)
print(type(y[0]))
n_components = 2
pca = PCA(n_components=n_components)
X_pca = pca.fit_transform(X)
show_ellipse(X_pca, y, pca)下面讲解实现过程。
首先导入需要的库和数据集:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from matplotlib.patches import Ellipse
然后定义了一个函数 plot_point_cov(),用于计算样本点的协方差矩阵,并调用另一个函数 plot_cov_ellipse(),绘制置信椭圆。
代码中的cov变量是用于计算数据集协方差矩阵的。协方差矩阵用于描述多个变量之间的关系,其中对角线上的元素表示每个变量本身的方差,非对角线上的元素表示不同变量之间的协方差。
在函数plot_cov_ellipse()中使用协方差矩阵计算数据集的特征向量和特征值。特征向量和特征值用于确定椭圆的大小和方向,以便绘制置信椭圆。
因为在二维空间中,椭圆的方向和大小可以用特征向量和特征值来描述。例如对于一个2x2的协方差矩阵cov,它有两个特征向量和两个特征值,分别表示数据集在两个主要方向上的方差和偏移。特征向量的方向决定了椭圆的主轴方向,而特征值的大小则决定了椭圆沿每个主轴的长度。
在函数plot_cov_ellipse()中,先使用np.linalg.eigh()函数计算协方差矩阵cov的特征值和特征向量,然后按特征值从大到小的顺序排序,这样可以确保主轴方向是正确的。然后根据主轴方向的角度和特征值计算椭圆的宽度和高度,进而绘制置信椭圆。函数np.degrees()用于将弧度转换为角度,函数np.arctan2()用于计算角度。
np.degrees()该函数使用的公式:角度=弧度*180/pi
np.degrees()函数的参数是np.arctan2(*vecs[:, 0][::-1]),它表示计算向量vecs中第一列(即下标为 0 的列)的极角(即与 x 轴的夹角)并将结果转换为角度制。具体来说,
vecs[:, 0]表示选取vecs中所有行的第一列组成的向量,[::-1]表示将该向量反转,从而得到与arctan2函数所需的参数格式一致的向量。然后,
np.arctan2()函数接收两个参数,表示计算以这两个参数组成的向量为起点,与原点连接的向量的极角。这里第一个参数是反转后的向量,即vecs[:, 0][::-1],第二个参数未给出,因此默认为 1。最后,
np.degrees()函数将弧度制的极角值转换为角度制。因此,整个代码行的作用是计算向量vecs的第一列的极角,并将结果转换为角度制。
vals, vecs = eigsorted(cov)其目的是计算输入协方差矩阵的特征值和特征向量并返回排好序的结果。特征值(eigenvalues)是协方差矩阵的一个重要属性,代表着每个特征向量的方差。在PCA中,特征值告诉我们每个主成分解释方差的大小。排序特征值后,我们可以选择最大的K个特征值来保留大部分数据的方差。
特征向量(eigenvectors)是PCA中另一个重要的概念,它们是协方差矩阵的正交基向量。每个特征向量对应着一个特征值。它们可以用来表示主成分的方向,PCA中的主成分就是按特征值大小排序后的特征向量。PCA的主要目的就是通过旋转坐标系来最大化每个主成分方差。
特征向量在这里被用来求出主成分的方向。在函数中,特征向量通过
vecs[:, order]得到,[:, order]表示选中所有行(:)和按照特定顺序排序的所有列(order)。这些特征向量就是主成分方向的坐标轴,可以用来画出置信区间椭圆的角度。椭圆的角度可以通过主成分方向的坐标轴与水平轴的夹角得到。在给定的代码中,
theta被计算为np.degrees(np.arctan2(*vecs[:, 0][::-1])),其中arctan2()计算向量的反正切值,[::-1]表示按照相反的顺序取向量的元素。np.degrees()将弧度转换为角度。
def plot_point_cov(points, nstd=3, ax=None, **kwargs):# 求所有点的均值作为置信圆的圆心pos = points.mean(axis=0)# 求协方差矩阵cov = np.cov(points, rowvar=False)return plot_cov_ellipse(cov, pos, nstd, ax, **kwargs)def plot_cov_ellipse(cov, pos, nstd=3, ax=None, **kwargs):def eigsorted(cov):cov = np.array(cov)vals, vecs = np.linalg.eigh(cov)order = vals.argsort()[::-1]return vals[order], vecs[:, order]if ax is None:ax = plt.gca()vals, vecs = eigsorted(cov)theta = np.degrees(np.arctan2(*vecs[:, 0][::-1]))width, height = 2 * nstd * np.sqrt(vals)ellip = Ellipse(xy=pos, width=width, height=height, angle=theta, **kwargs)ax.add_artist(ellip)return ellip
最后,定义了一个函数 show_ellipse(),用于绘制样本点和置信椭圆。
'''画置信圆'''
def show_ellipse(X_pca, y, pca, flag=1):# 定义颜色colors = ['tab:blue', 'tab:orange', 'seagreen']regions = ['Ethiopia', 'Somalia', 'Kenya']# 定义分辨率plt.figure(dpi=300, figsize=(8, 6))# 三分类则为3for i in range(0, 3):pts = X_pca[y == int(i), :]new_x, new_y = X_pca[y==i, 0], X_pca[y==i, 1]plt.plot(new_x, new_y, '.', color=colors[i], label=regions[i], markersize=14)plot_point_cov(pts, nstd=3, alpha=0.25, color=colors[i])# 添加坐标轴plt.xlim(-3.5, 4.5)plt.ylim(-1.5, 1.7)plt.xticks(size=16, family='Times New Roman')plt.yticks(size=16, family='Times New Roman')font = {'family': 'Times New Roman', 'size': 16}plt.xlabel('PC1 ({} %)'.format(round(pca.explained_variance_ratio_[0] * 100, 2)), font)plt.ylabel('PC2 ({} %)'.format(round(pca.explained_variance_ratio_[1] * 100, 2)), font)plt.legend(prop={"family": "Times New Roman", "size": 9}, loc='upper right')plt.show()以数据集鸢尾花为例进行PCA降维,并使用上面代码画置信圆。
import pandas as pd
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
labels = ['setosa', 'versicolor', 'virginica']
iris = load_iris()
X = iris.data
y = iris.target_names[iris.target]print("y length--------", len(y))
y_category = pd.Categorical(y,ordered=True,categories=['setosa', 'versicolor', 'virginica'])y = y_category.codes
print(y)
print(y.shape)
print(type(y[0]))
n_components = 2
pca = PCA(n_components=n_components)
X_pca = pca.fit_transform(X)
show_ellipse(X_pca, y, pca)上面解析均为学习使用,如有问题请指正。
相关文章:

python实现PCA降维画分类散点图并标出95%的置信区间
此代码以数据集鸢尾花为例,对其使用PCA降维后,绘制了三个类别的样本点和对应的置信圆(即椭圆)。先放效果图。 下面是完整代码: from matplotlib.patches import Ellipsedef plot_point_cov(points, nstd3, axNone, **…...

Mysql高级之索引结构详解
Mysql的索引详解1.索引定义2.索引结构2.1数据结构分析2.1.1熟知的数据结构2.1.2分析为什么这么多的数据结构不全适用于索引结构2.2Hash结构2.3B tree结构3.索引分类3.1聚集索引(聚簇索引)3.2非聚集索引(稀疏索引)3.3联合索引3.4主…...
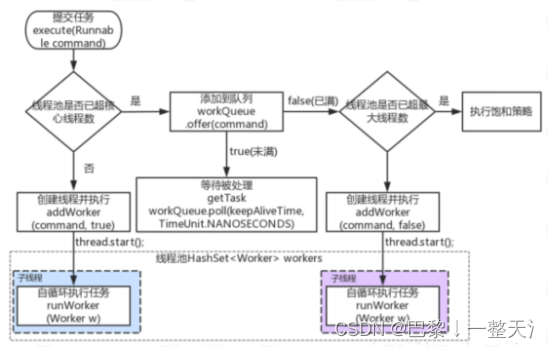
【线程-J.U.C】
Lock J.U.C最核心组件,Lock接口出现之前,多线程的并发安全只能由synchronized处理,但java5之后,Lock的出现可以解决synchronized的短板,更加灵活。 Lock本质上是一个接口,定义了释放锁(unlock&…...
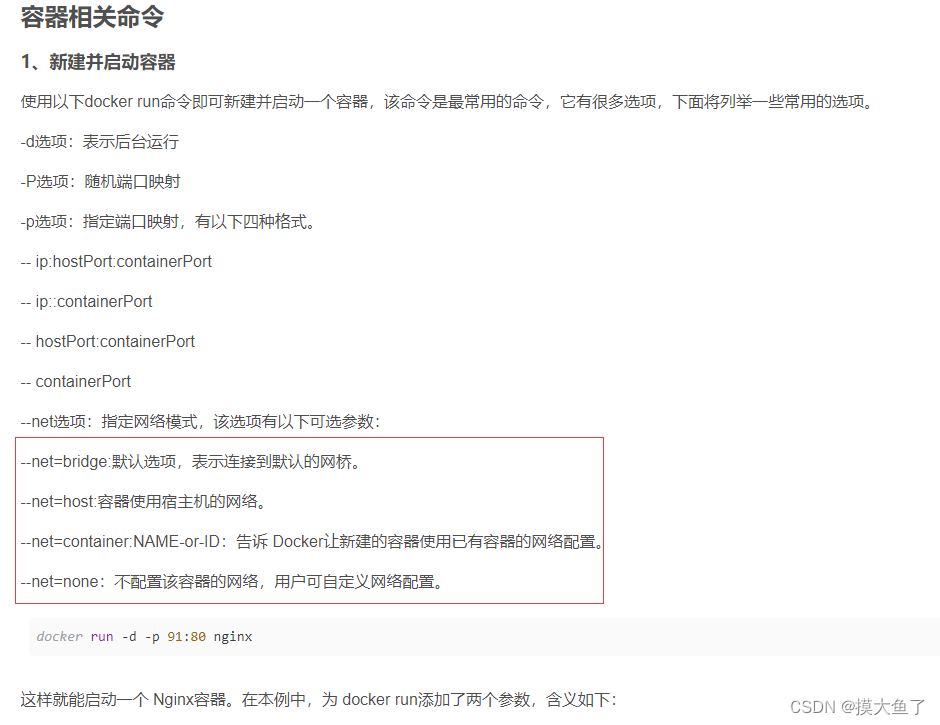
docker布署spring boot jar包项目
目录docker 安装创建目录制作镜像启动容器查看日志docker 安装 Docker安装、详解与部署 创建目录 服务器中创建一个目录,存放项目jar包和Dockerfile 文件 mkdir /目录位置创建目录后创建Dockerfile文件,上传jar包到同一目录下 创建dockerfile vim Doc…...

极简Vue3教程--Pinia状态管理
Pinia(发音为/piːnjʌ/,如英语中的“peenya”)是最接近pia(西班牙语中的菠萝)的词;Pinia开始于大概2019年,最初是作为一个实验为Vue重新设计状态管理,让它用起来像组合式API&#x…...

常用的map转bean互转方法
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 常用的map转bean互转方法一、hutool工具类二、fastjson工具类三、beanutils_BeanUtils工具类 不太好用四、cglib BeanMap工具类 不太好用五、reflect 反射来玩 不太好玩六、I…...

2.4G收发一体芯片NRF24L01P跟国产软硬件兼容 SI24R1对比
超低功耗高性能 2.4GHz GFSK 无线收发器芯片Si24R1,软硬件兼容NRF24L01P. Si24R1 是一颗工作在 2.4GHz ISM 频段,专为低功耗无线场合设计,集成嵌入式ARQ 基带协议引擎的无线收发器芯片。工作频率范围为 2400MHz-2525MHz,共有 126个…...
——单一职责原则、开放-关闭原则)
设计模式之七大原则(一)——单一职责原则、开放-关闭原则
目录一、设计模式的目的二、设计模式的七大原则1.单一职责原则2.开放-关闭原则一、设计模式的目的 设计模式的目的是为了提高代码重用性、可读性、可扩展性、可靠性,使得程序呈现出高内聚、低耦合的特性。 代码重用性(相同功能的代码,不用多…...
)
C++ set、unordered_set、multiset它们之间的区别与一些使用方法(不断更新)
set、unordered_set、multiset是什么?以及它们之间的区别 首先,它们三个都是C标准库提供的关联容器中的一种。只不过set、multiset容器是有序的,而unordered_set容器是无序的 std::set 是 C 标准库中的一个容器,其存储的元素按设…...
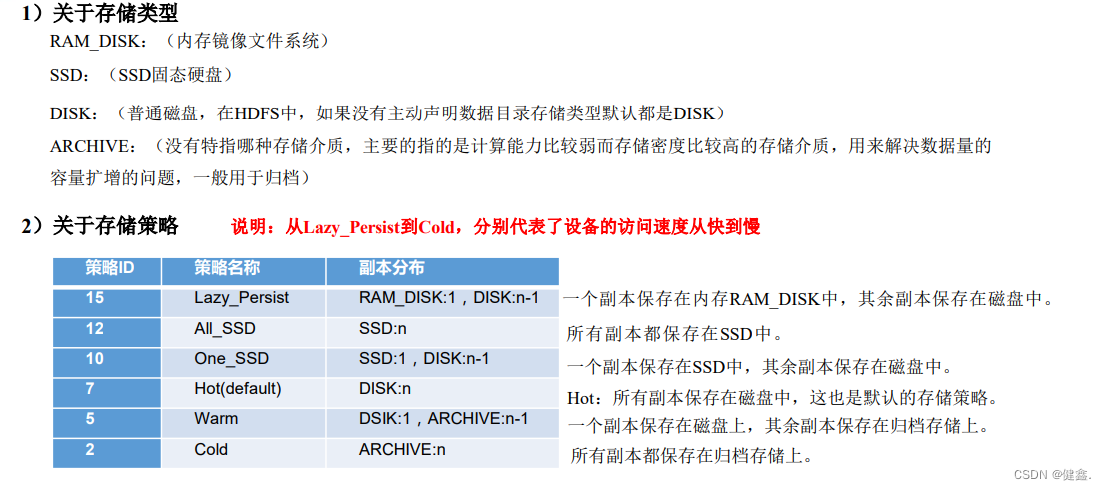
hadoop调优
hadoop调优 1 HDFS核心参数 1.1 NameNode内存生产配置 1.1.1 NameNode内存计算 每个文件块大概占用150byte,如果一台服务器128G,能存储的文件块如下 128 (G)* 1024(MB) * 1024(KB) * 1024(Byte) / 150 Byte 9.1 亿 1.1.2 Hadoop2.x 在Hadoop2.x中…...
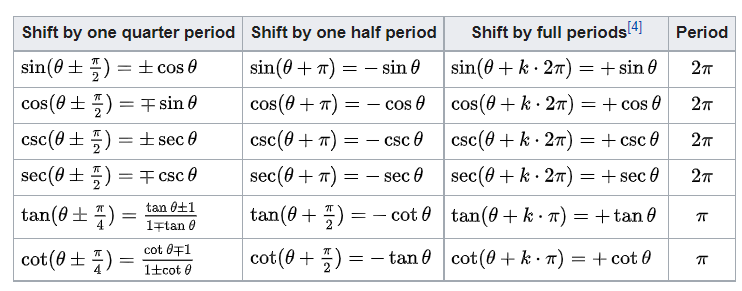
EM@三角函数诱导公式
文章目录诱导公式单位圆坐标和三角函数记忆口诀符号看象限奇变偶不变例常用诱导公式🎈常用部分(5对)倒数关系六种三角函数间的转换关系小结ReflectionsShifts and periodicity诱导公式 诱导公式 - 维基百科,自由的百科全书 (wikipedia.org) 单位圆坐标…...

是不是只能学IT互联网技术才有发展前途?
当然不是,三百六十行,行行出状元。 但我们需要认清一个现实是,我们正处于一个信息爆炸的时代,掌握紧跟潮流的技术,才可以让我们更自信地面对每天的生活,才有多余的精力、财力来享受生活。“人生在世&#…...

Linux 进程:exit和_exit的辨析
目录1.接口与函数2.缓冲区3.exit 与 _exit(1)_exit(2)exit这里来认识exit函数和 _exit接口 ,它们的作用是类似的,都是在调用后退出程序,可以在程序的任何地方调用。 1.接口与函数 exit函数和_exit接口,一个函数,一个…...
智能电子标签——商超版价签
2.1英寸TFT黑白电子价签 ★ 快速变价,高效运营 ★ 市场实用,布局物联网未来 ★ 更好客户体验 ★ 降低系统成本,具备竞争力 ★ 2.1英寸黑白红电子价签 ★ 电池低能耗,常规使用三年 ★ 穿透力强不慣障碍 ★ 2.4G载波&#x…...
计算机网络自检
1 计网体系结构 因特网结构: 计网三个组成成分: 工作方式-其中2个部分: 功能-两个子网: 5个XAN分别是: 传输技术,两者的主要区别: 4种基本网络拓扑结构: 3种交换技术: 协…...

DC真实数据都有哪些?Filecoin为DC数据存储的解决方案又是什么?
对于生活在数字时代的我们而言,数据或许就和平日呼吸的空气一样,已经不需要我们再去思考其概念。我们的日常生活中无时无刻都有数据的身影,日常的购物消费、出行、学习、记录,当我们每天生活有数字化加持的小区里,工作…...
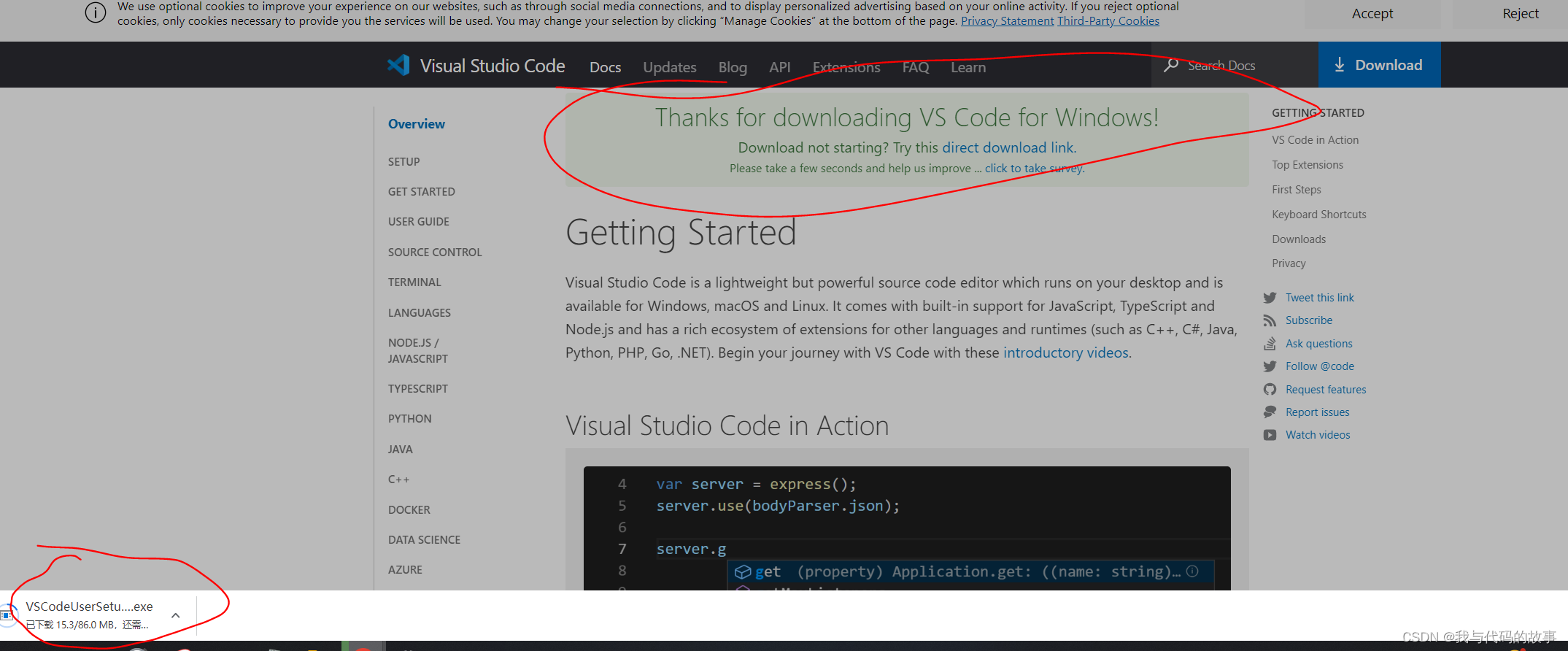
解决vscode无法自动更新
一.前言 要在vscode里面安装插件,被提示版本不匹配,然后得更新,然后我发现我的'帮助'菜单栏下没有检查更新,然后我去&…...

315线上知识竞赛答题活动方案及模板分享
315线上知识竞赛答题活动方案及模板分享在315国际消费者权益日来临之际, 很多单位推出有奖知识竞答, 希望大家在了解专业知识的同时, 还可以拿到自己喜欢的奖品!这是消费者委员会和监管局联合举办的“315消费知识在线有奖竞答”活…...
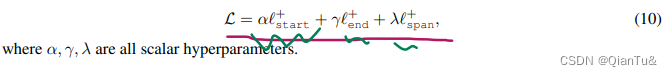
论文复现-2:代码部分
以CONLL03数据集为例 文章目录1 整体框架2 数据结构2.1 原始数据集2.2 处理之后的数据集3 代码部分3.0 模型参数3.1 数据预处理3.2 模型方法3.1.1 定义表示的学习权重项的学习双塔模型3.2.2 forward3.3 损失函数3.4 训练与推理Ablation study训练实例1 整体框架 任务是实体识别…...
Linux开放的端口太多了?教你一招找出所有开放的端口,然后直接干掉!
基于服务器安全性维护的目的,查看所有开放的端口是通常采取的第一步,从中检查出可疑或者不必要的端口并将其关掉。关于查看开放的端口,方法不止一种,比如lsof 命令,还可以使用 ss 命令。 查看开放的端口 今天我们就介…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
