理论U3 决策树
文章目录
- 一、决策树算法
- 1、基本思想
- 2、构成
- 1)节点
- 3)有向边/分支
- 3、分类步骤
- 1)第1步-决策树生成/学习、训练
- 2)第2步-分类/测试
- 4、算法关键
- 二、信息论基础
- 1、概念
- 2、信息量
- 3、信息熵:
- 二、ID3 (Iterative Dichotomiser 3)算法
- 1、基本思想:
- 2、熵引入
- 1)经验熵
- 2)条件熵
- 3)经验条件熵
- 4)信息增益(information gain)
- 3、算法
- 4、算法案例
- 5、算法特点
- 三、ID3算法问题
- 1、 属性筛选度量标准
- 2、 剪枝处理
- 1)问题
- 2)解决
- 3)案例
- 3、 连续值处理
- 4、 缺失值处理
- 5、不同代价属性的处理
一、决策树算法
1、基本思想
基本思想:采用自顶向下的递归方法,(以信息熵为度量)构造一棵(熵值下降最快的)树,(到叶子节点处的熵值为零)此时每个叶节点中的实例都属于同一类
2、构成
决策树是一种树型结构,由结点和有向边组成
1)节点
- 内部结点表示一个属性或特征
- 叶结点代表一种类别
3)有向边/分支
分支代表一个测试输出
3、分类步骤
1)第1步-决策树生成/学习、训练
利用训练集建立(并精化)一棵决策树,建立决策树模型。这个过程实际上是一个从数据中获取知识,进行机器学习的过程
step 1:选取一个属性作为决策树的根结点,然后就这个属性所有的取值创建树的分支。
step 2:用这棵树来对训练数据集进行分类:
- 如果一个叶结点的所有实例都属于同一类,则以该类为标记标识此叶结点。
- 如果所有的叶结点都有类标记,则算法终止
step 3:否则,选取一个从该结点到根路径中没有出现过的属性为标记标识该结点,然后就这个属性所有的取值继续创建树的分支;重复算法步骤step 2
2)第2步-分类/测试
利用生成的决策树对输入数据进行分类。对输入的记录,从根结点依次测试记录的属性值,直到到达某个叶结点,从而找到该记录所在的类。
4、算法关键
建立决策树的关键,即在当前状态下选择哪个属性作为分类依据
目标:每个分支节点的样本尽可能属于同一类别,即节点的“纯度”(purity)越来越高;最具区分性的属性!
根据不同目标函数,建立决策树主要有以下三种算法
◼ ID3: 信息增益
◼ C4.5: 信息增益率
◼ CART:基尼指数
二、信息论基础
1、概念
信息论与概率统计中,熵表示随机变量不确定性的大小,是度量样本集合纯度最常用的一种指标
2、信息量
信息量:具有确定概率事件的信息的定量度量
定义: I ( x ) = − l o g 2 p ( x ) I(x)=-log_2p(x) I(x)=−log2p(x) 其中p(x)为事件x发生的概率
3、信息熵:
事件集合的信息量的平均值。
定义: H ( x ) = ∑ i h ( x i ) = ∑ i p ( x i ) I ( x i ) = − ∑ i p ( x i ) l o g 2 p ( x i ) H(x) = \sum_{i}h(x_i)=\sum_{i} p(x_i)I(x_i)=-\sum_{i} p(x_i)log_2p(x_i) H(x)=∑ih(xi)=∑ip(xi)I(xi)=−∑ip(xi)log2p(xi)
熵定义了一个函数(概率密度函数pdf)到一个值(信息熵)的映射
p ( x ) → H p(x) → H p(x)→H (函数→数值)
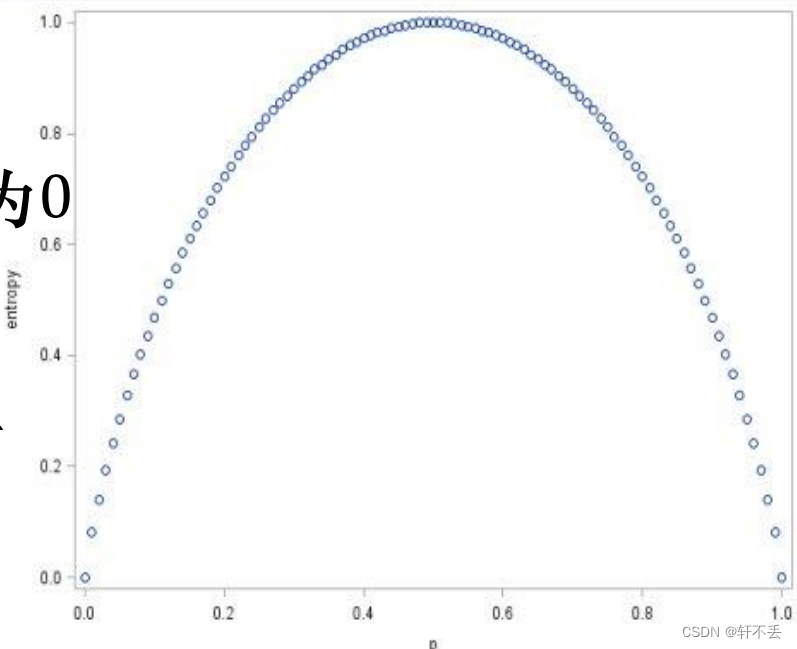
熵是随机变量不确定性的度量:
◼ 不确定性越大,熵值越大
◼ 若随机变量退化成定值,熵为0
二、ID3 (Iterative Dichotomiser 3)算法
ID3算法是一种最经典的决策树学习算法。
1、基本思想:
以信息熵为度量,用于决策树节点的属性选择,每次优先选取信息增益最大的属性,亦即能使熵值变为最小的属性,以构造一颗熵值下降最快的决策树,到叶子节点处的熵值为0。此时,每个叶子节点对应的实例集中的实例属于同一类。
熵值下降 → 无序变有序
2、熵引入
1)经验熵
假设当前样本集合D 中第c(c=1,2,…,C)类样本所占比例为 p c p_c pc(c=1,2,…,C),则D 的经验信息熵(简称经验熵)定义为:
H ( D ) = − ∑ c = 1 C p c l o g 2 p c = − ∑ c = 1 C D c D l o g 2 D c D H(D)=-\sum_{c=1}^{C}p_clog_2p_c=-\sum_{c=1}^{C}\frac{D_c}{D}log_2\frac{D_c}{D} H(D)=−∑c=1Cpclog2pc=−∑c=1CDDclog2DDc
H(D)的值越小,则D 的纯度越高
2)条件熵
对随机变量 ( X , Y ) (X, Y) (X,Y),联合分布为: p ( X = x i , Y = y i ) = p i j p(X=x_i,Y=y_i)=p_{ij} p(X=xi,Y=yi)=pij
条件熵 H ( Y ∣ X ) H(Y |X ) H(Y∣X) 表示在已知随机变量X 的条件下,随机变量Y的不确定性:
H ( Y ∣ X ) = − ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y|X)=-\sum_{i=1}^{n}p_iH(Y|X=x_i) H(Y∣X)=−∑i=1npiH(Y∣X=xi)
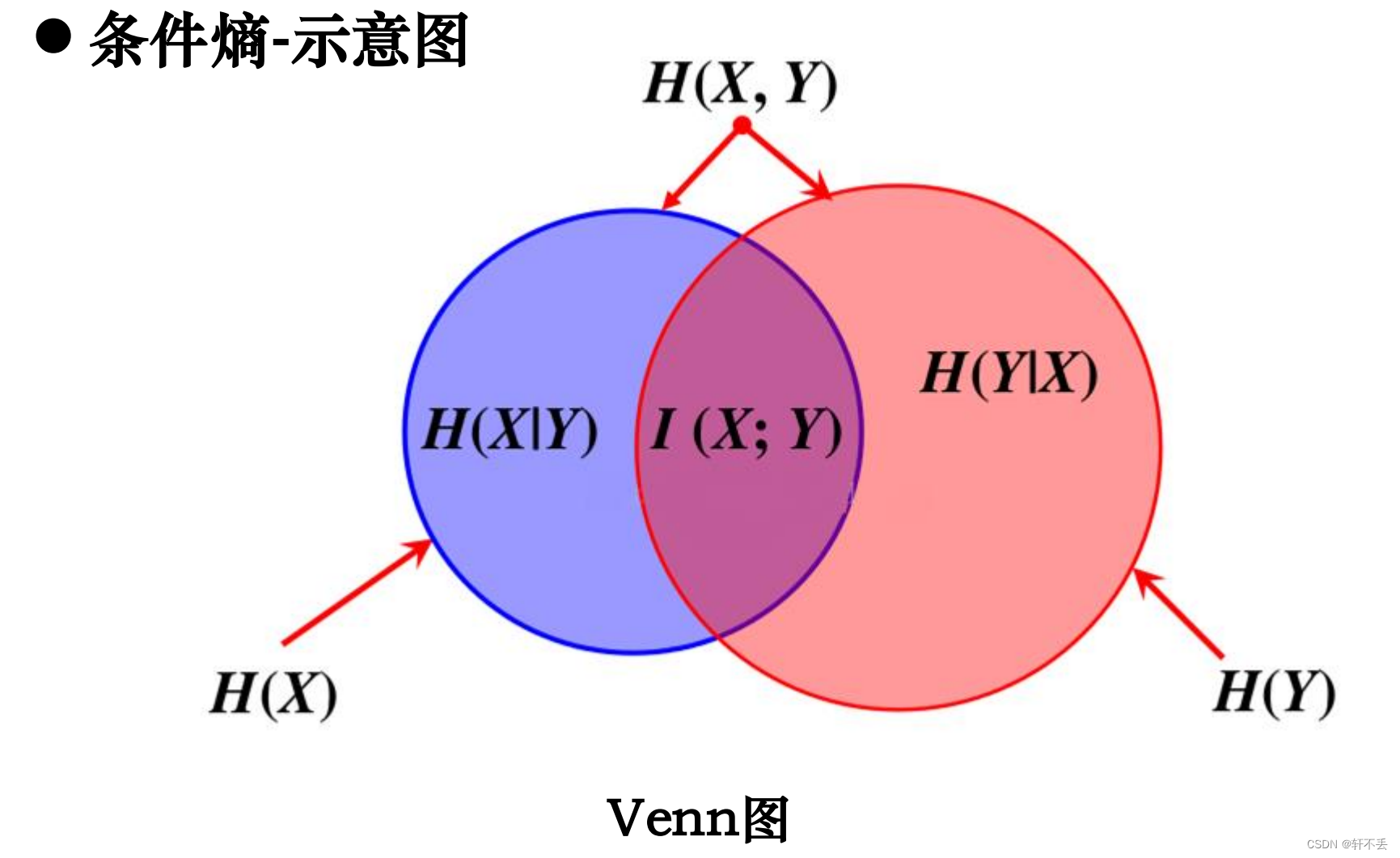
可证明:条件熵𝐻(Y|X)相当于联合熵𝐻(𝑋,𝑌)减去单独的熵𝐻(X),即
H ( Y ∣ X ) = H ( X , Y ) − H ( X ) H(Y|X)=H(X,Y)-H(X) H(Y∣X)=H(X,Y)−H(X)

3)经验条件熵

即特征a的信息对样本D 的信息的不确定性减少的程度
4)信息增益(information gain)
特征 a 对训练数据集 D 的信息增益 G ( D , a ) G(D, a) G(D,a) ,定义为集合D 的经验熵 H(D) 与特征 a 给定条件下 D 的经验条件熵 H ( D ∣ a ) H(D | a) H(D∣a) 之差,即
G ( D , a ) = H ( D ) − H ( D ∣ a ) = H ( D ) − ∑ n = 1 N D n D H ( D n ) G(D,a)=H(D)-H(D|a)=H(D)-\sum_{n=1}^{N}\frac{D^n}{D}H(D^n) G(D,a)=H(D)−H(D∣a)=H(D)−∑n=1NDDnH(Dn)
ID3算法即是以此信息增益为准则,对每次递归的节点属性进行选择的
3、算法

4、算法案例
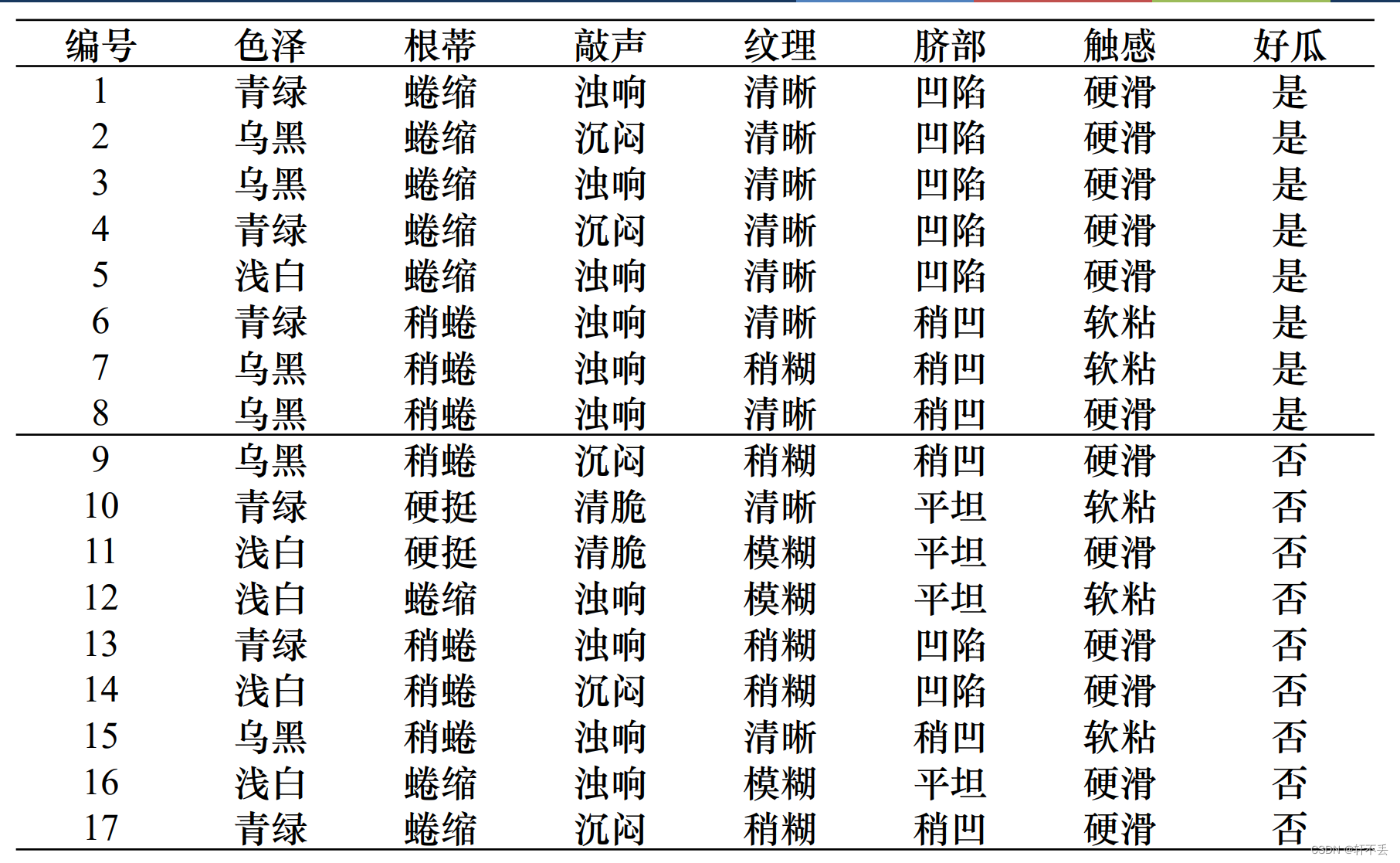


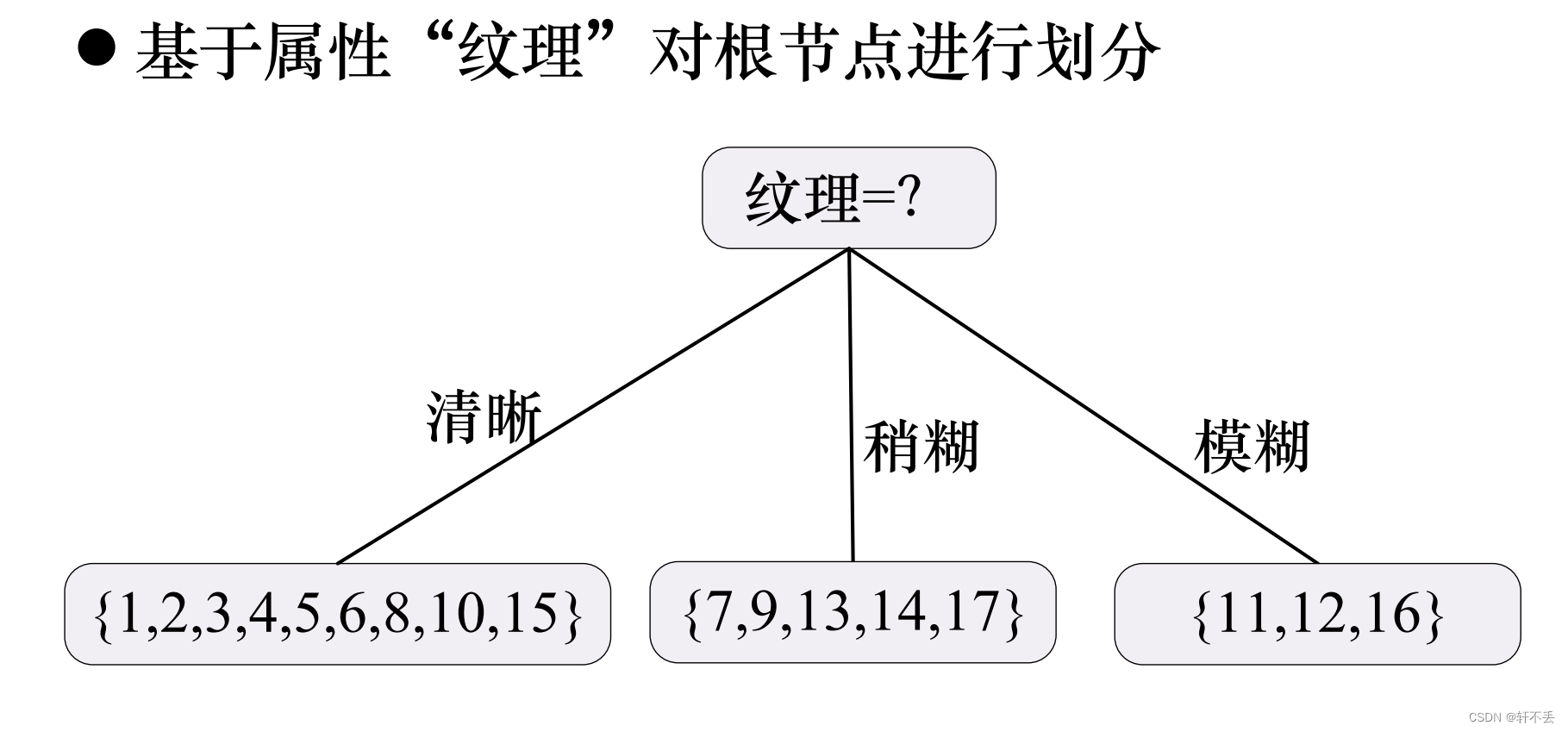

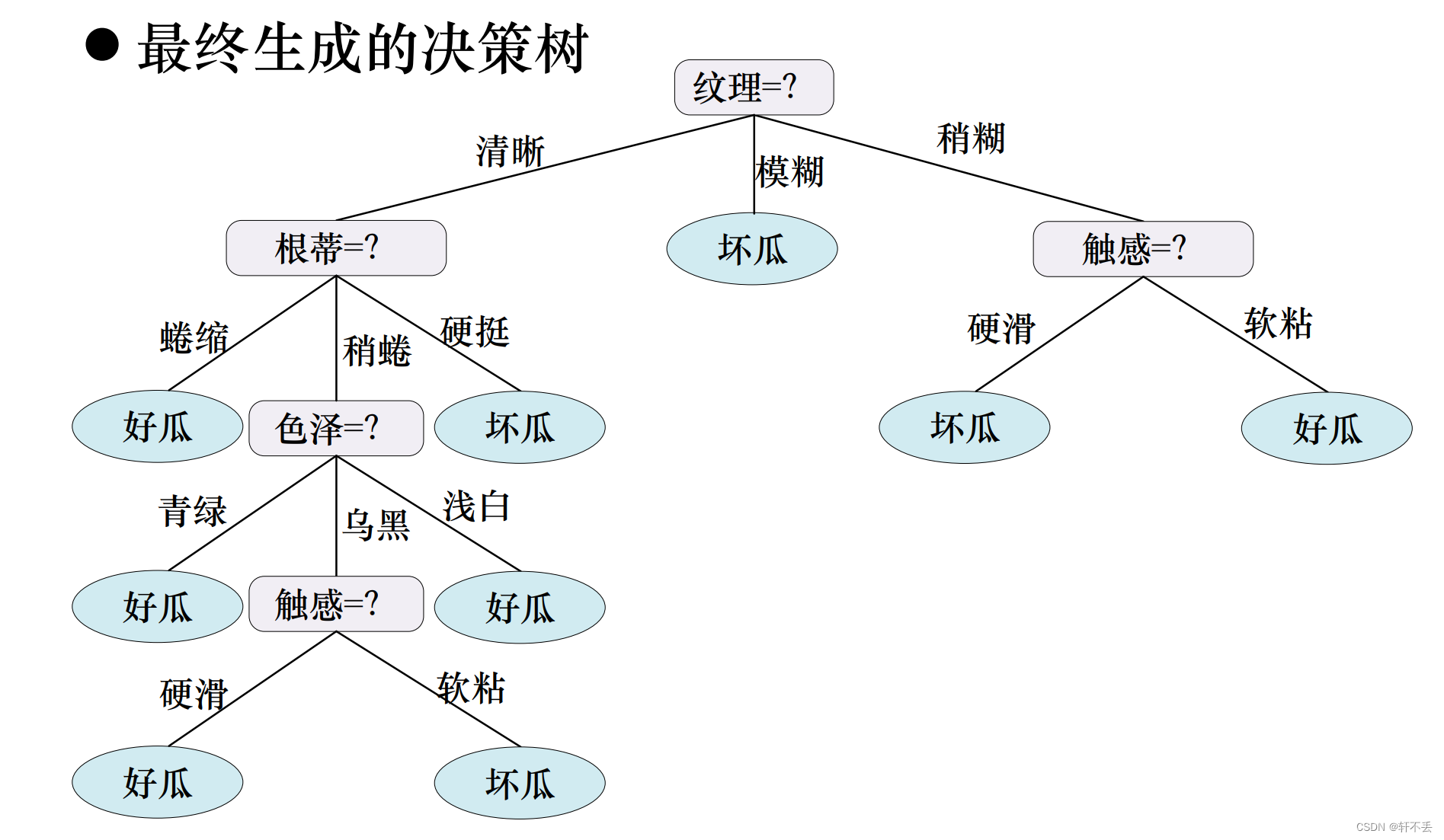
5、算法特点
最大优点是,它可以自学习:在学习的过程中,不需要使用者了解过多背景知识,只需要对训练实例进行较好的标注,就能够进行学习。
决策树的分类模型是树状结构,简单直观,比较符合人类的理解方式。
可将决策树中到达每个叶节点的路径转换为IF—THEN形式的分类规则,这种形式更有利于理解。
从一类无序、无规则的事物(概念)中推理出决策树表示的分类规则。
三、ID3算法问题
信息增益偏好取值多的属性(分散,极限趋近于均匀分布)
1、 属性筛选度量标准
可能会受噪声或小样本影响,易出现过拟合问题。
结果训练出来的形状是一棵庞大且深度很浅的树,这样的划分是极为不合理的。
改进方法:
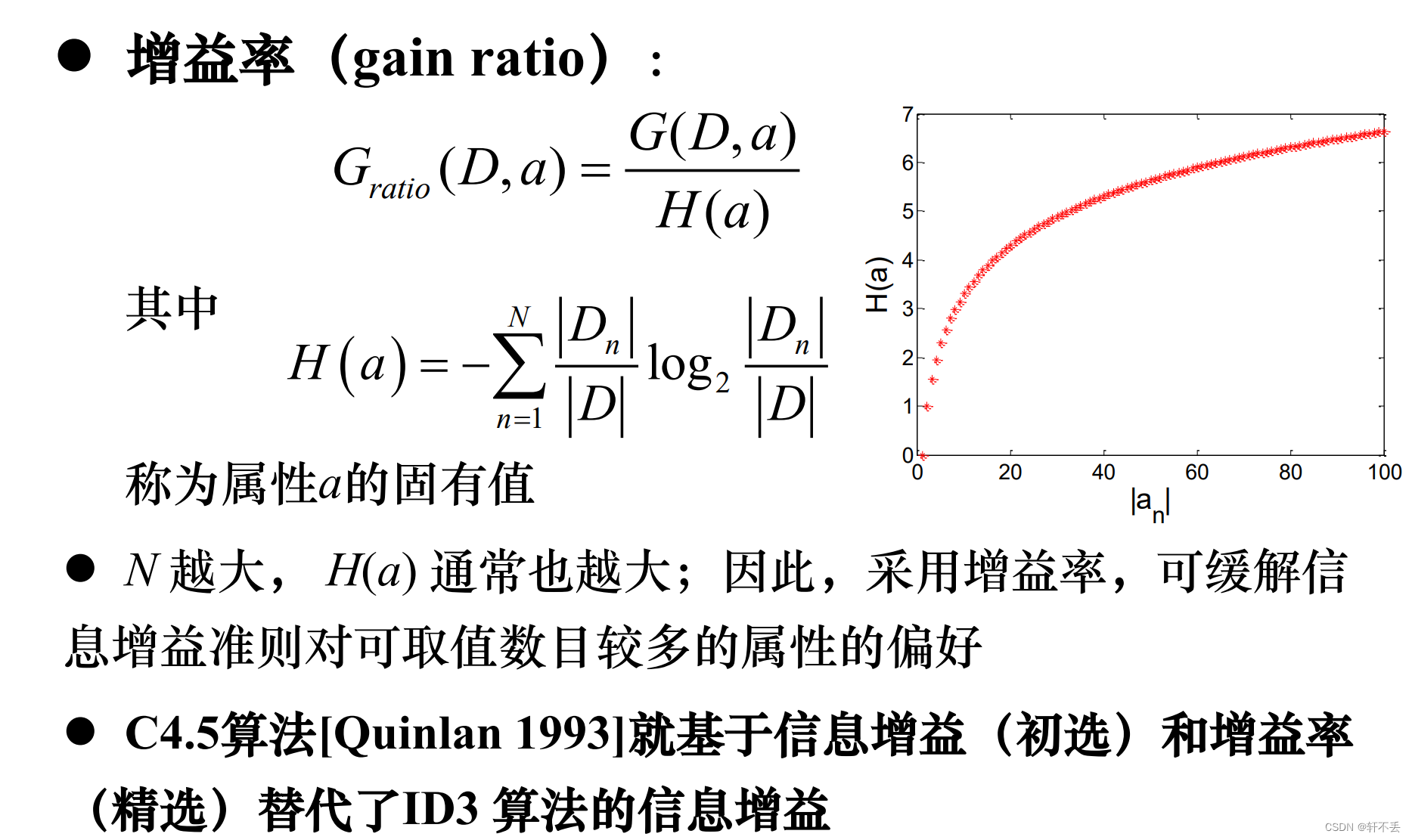

2、 剪枝处理
1)问题
无法处理连续值的属性。
决策树对训练数据有很好的分类能力,但对未知的测试数据未必有好的分类能力,泛化能力弱,即可能发生过拟合现象。
训练数据有噪声,对训练数据拟合的同时也对噪音进行拟合,影响了分类效果。
叶节点样本太少,易出现耦合的规律性,使一些属性恰巧可以很好地分类,但却与实际的目标函数并无关系。
2)解决
剪枝是决策树学习算法中对付“过拟合”的主要手段
-
预剪枝策略(pre-pruning):
决策树生成过程中,对每个节点在划分前进行估计,若划分不能带来决策树泛化性能提升,则停止划分,并将该节点设为叶节点
优点:预剪枝“剪掉了”很多没必要展开的分支,降低了过拟合的风险,并且显著减少了决策树的训练时间开销和测试时间开销
劣势:有些分支的当前划分有可能不能提高甚至降低泛化性能,但后续划分有可能提高泛化性能;预剪枝禁止这些后续分支的展开,可能会导致欠拟合 -
后剪枝策略(post-pruning):
先利用训练集生成决策树,自底向上对非叶节点进行考察,若将该叶节点对应子树替换为叶节点能带来泛化性能提升,则将该子树替换为叶节点
优点:优势:测试了所有分支,比预剪枝决策树保留了更多分支,降低了欠拟合的风险,泛化性能一般优于预剪枝决策树。
劣势:后剪枝过程在生成完全决策树后在进行,且要自底向上对所有非叶节点逐一评估;因此,决策树的训练时间开销要高于未剪枝决策树和预剪枝决策树
3)案例
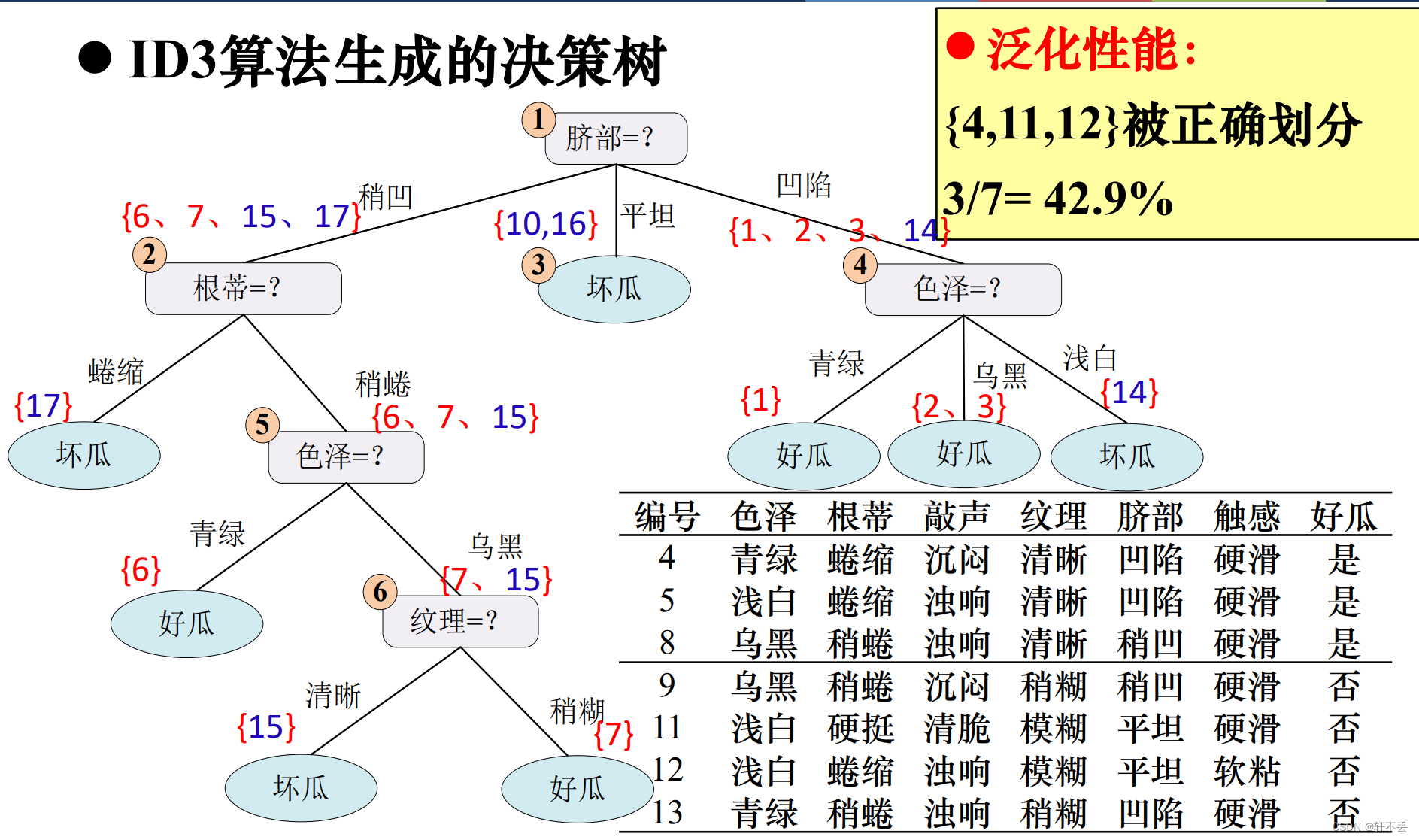
预剪枝算法


后剪枝算法
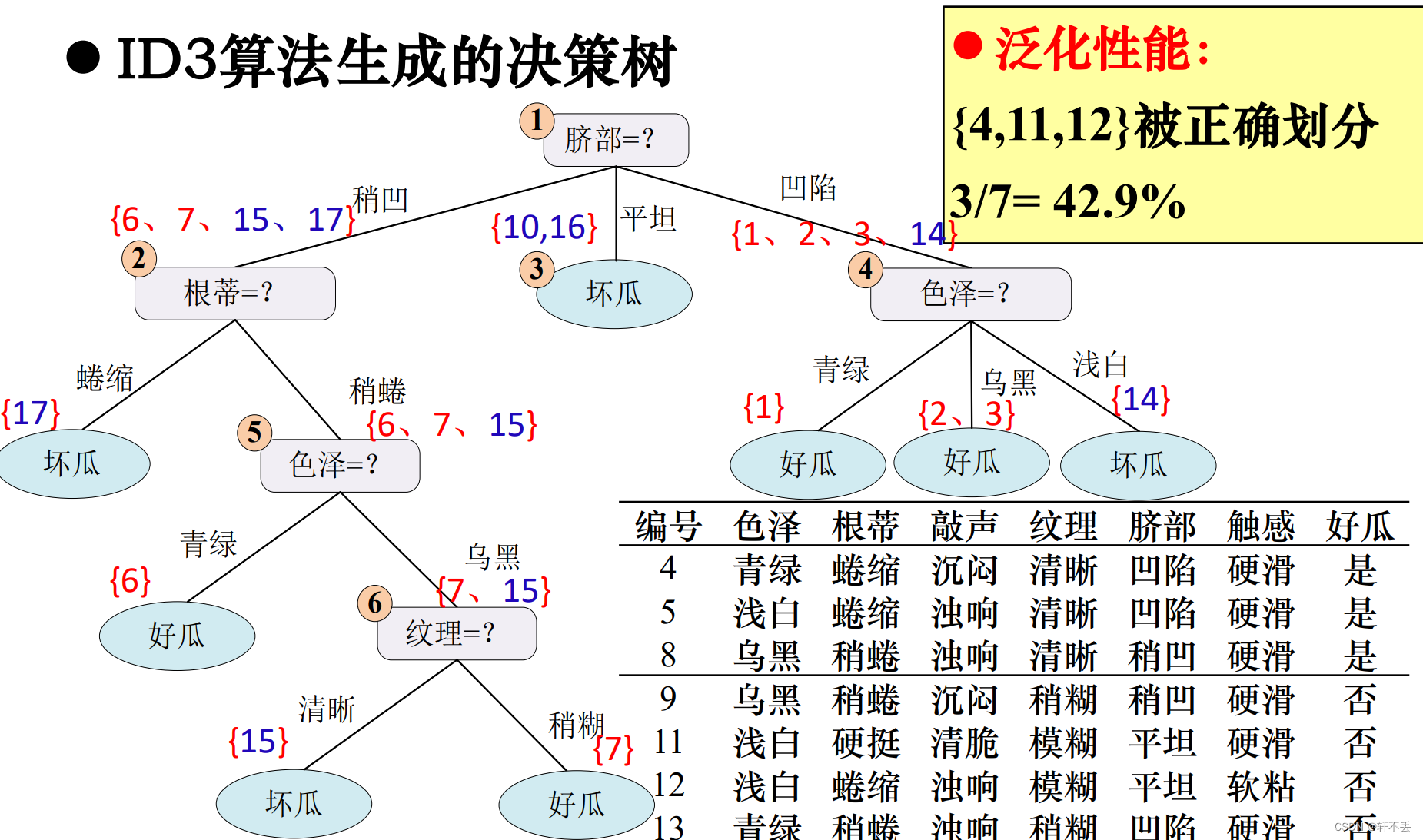





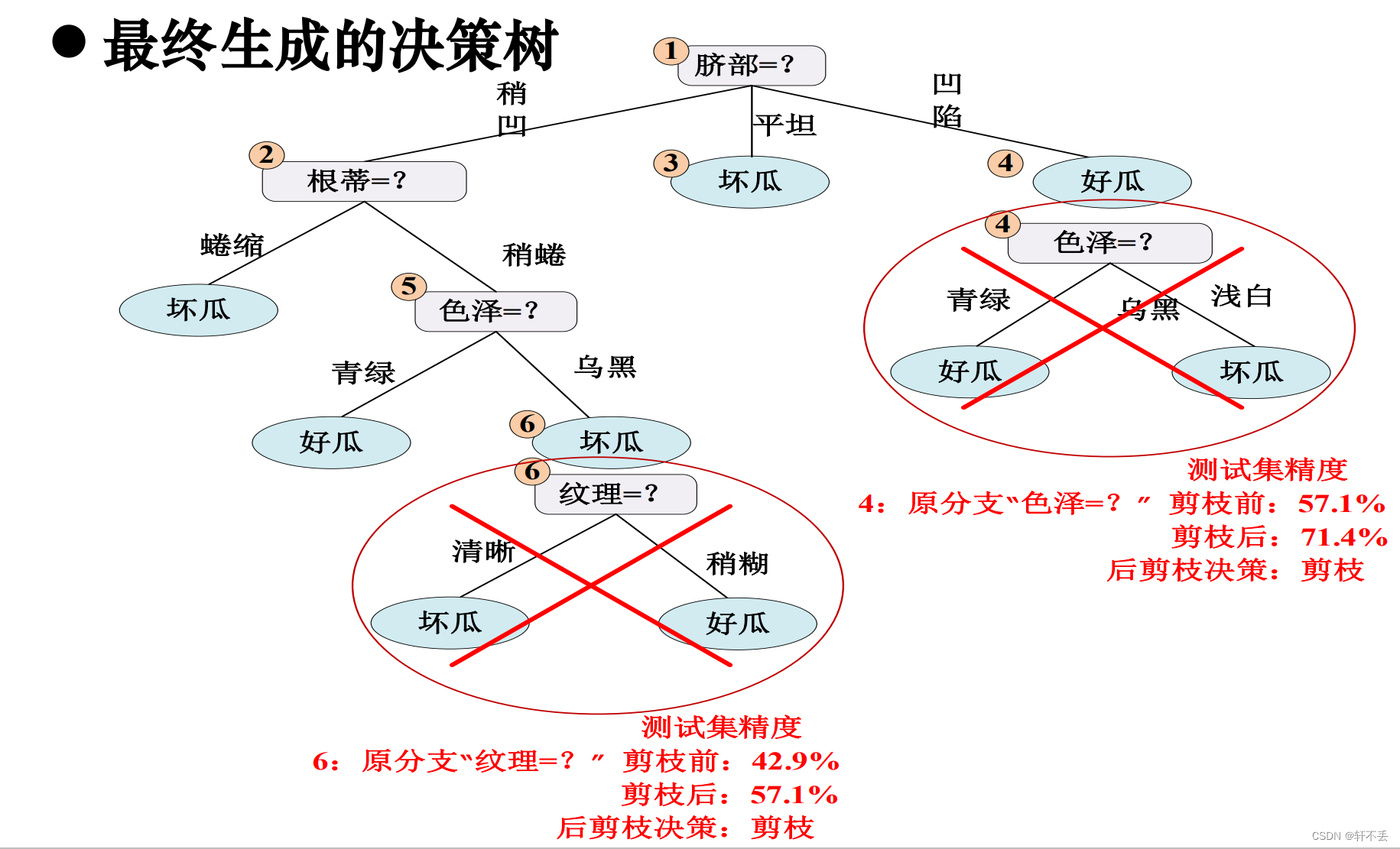
3、 连续值处理
无法处理属性值不完整的训练数据
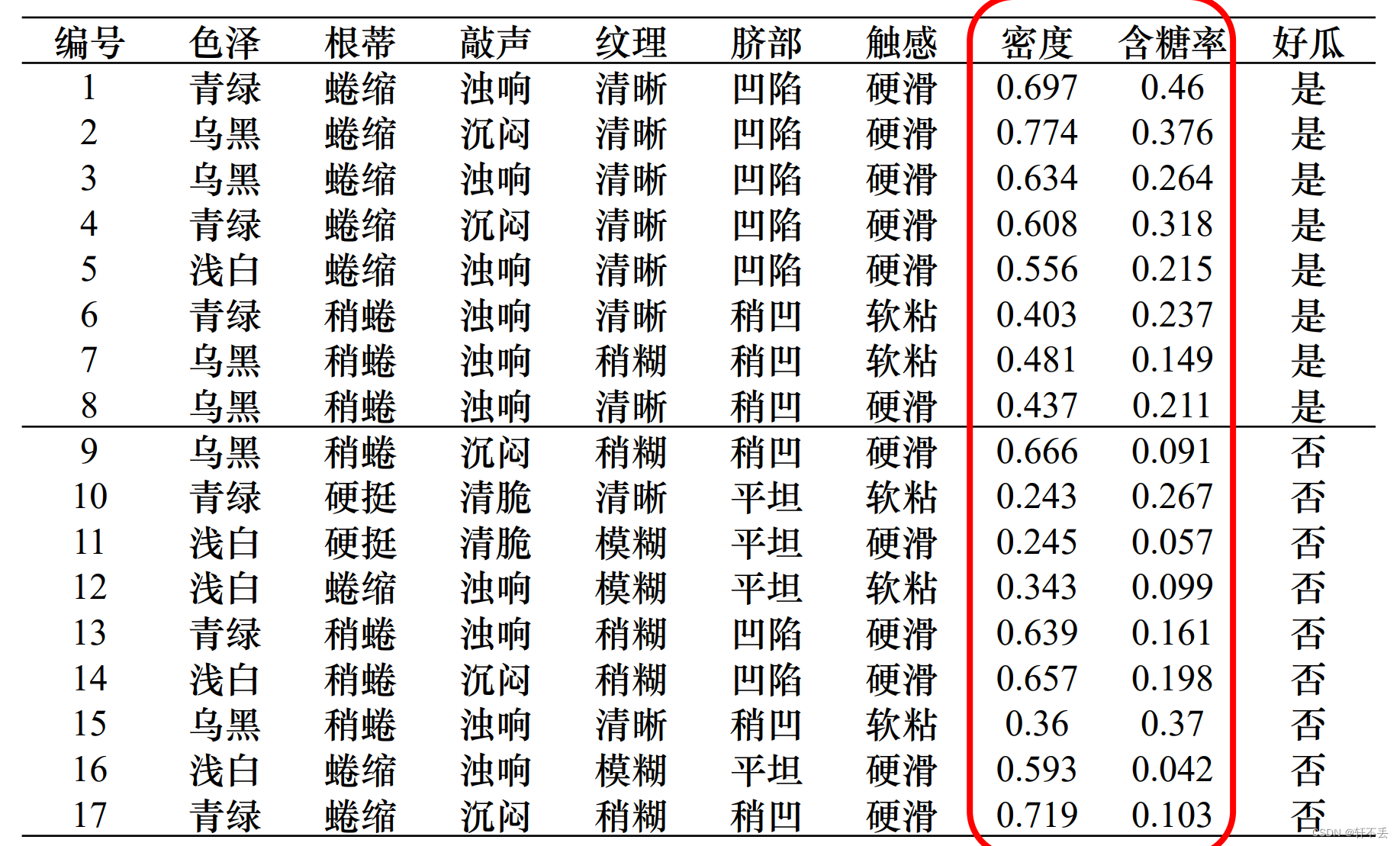
基本思想:采用二分法(bi-partition)进行离散化


4、 缺失值处理
无法处理不同代价的属性
前面假设:所有样本的属性完整
实际情况:存在不完整样本:即样本的某些属性缺失;特别是属性数目较多时
如果简单放弃不完整样本,会导致数据信息的浪费
实际中确实需要属性缺失情况下进行决策
◼ 不同代价属性的处理
需要解决的两个问题
- 如何在属性值缺失的情况下进行划分属性选择(计算信息增益)?



- 给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分?

案例:
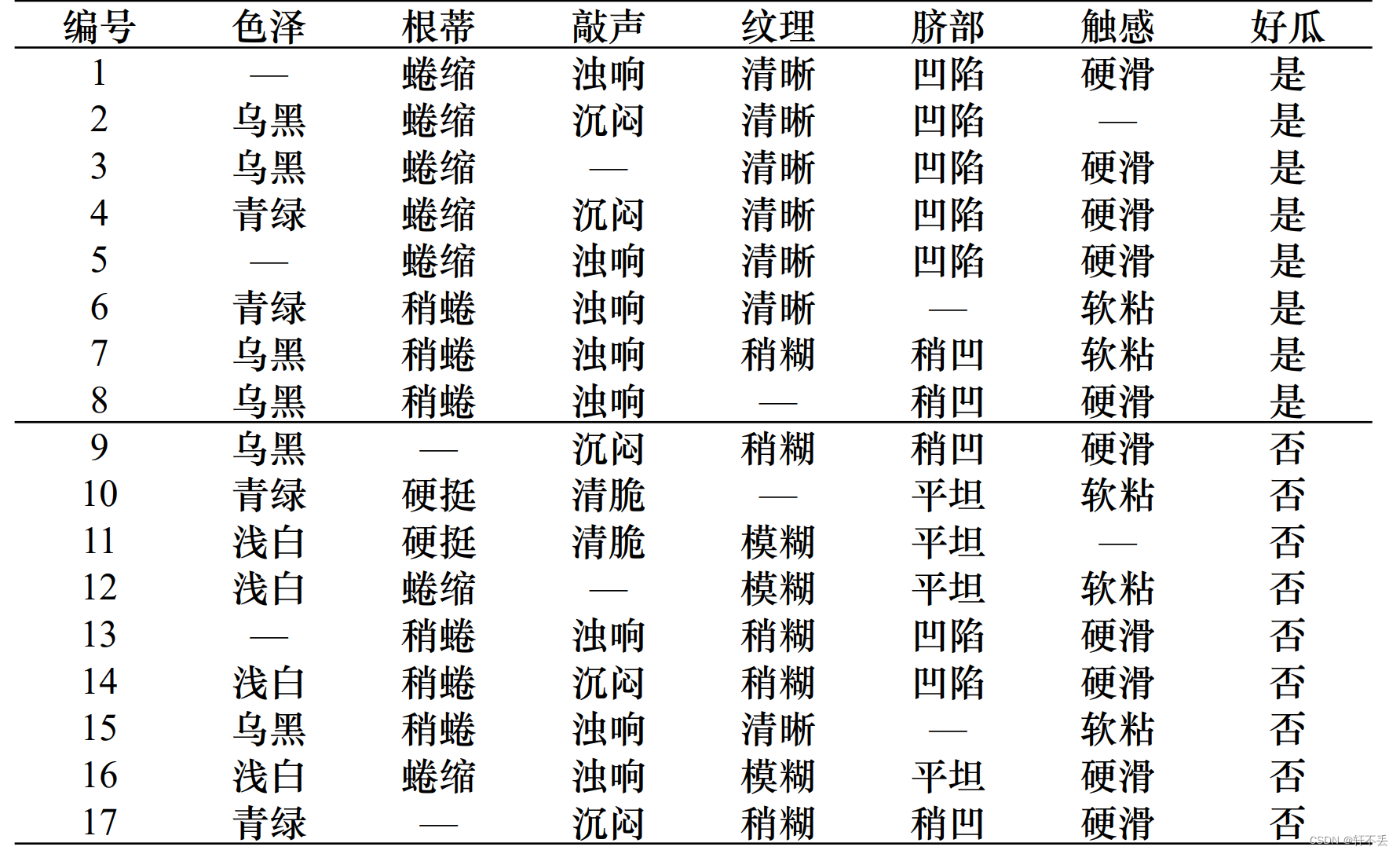



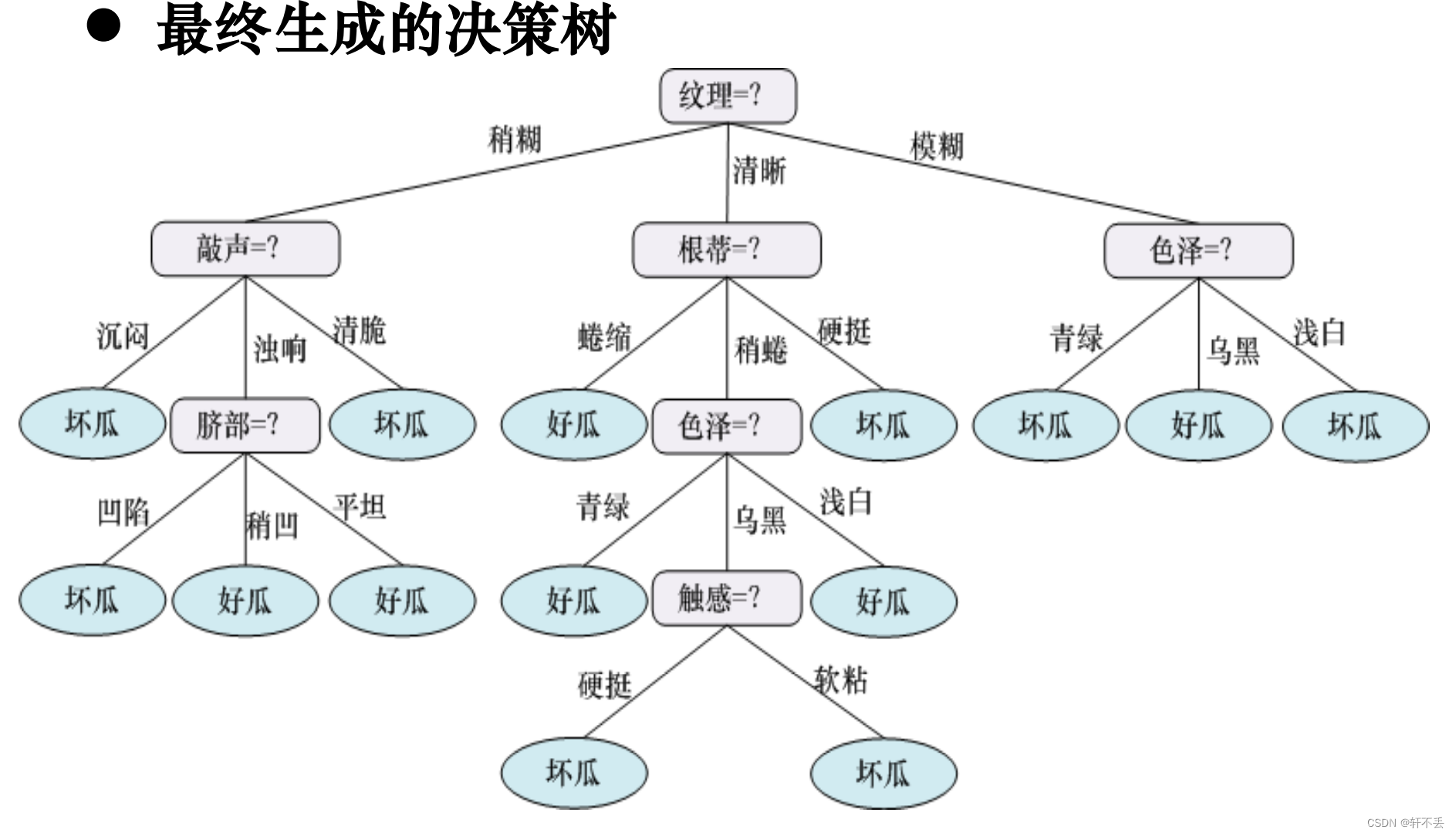
5、不同代价属性的处理
不同的属性测量具有不同的代价
在属性筛选度量标准中考虑属性的不同代价
优先选择低代价属性的决策树
必要时才依赖高代价属性

相关文章:

理论U3 决策树
文章目录 一、决策树算法1、基本思想2、构成1)节点3)有向边/分支 3、分类步骤1)第1步-决策树生成/学习、训练2)第2步-分类/测试 4、算法关键 二、信息论基础1、概念2、信息量3、信息熵: 二、ID3 (Iterative Dichotomis…...

Redis 常用操作
一、Redis常用的5种数据类型 字符串(String):最基本的数据类型,可以存储字符串、整数或浮点数。哈希(Hash):键值对的集合,可以在一个哈希数据结构中存储多个字段和值。列表…...

c# 使用Null合并操作符例子
在这个示例中,我们定义了两个字符串变量 name 和 defaultName。变量 name 被赋值为 null,而变量 defaultName 被赋值为 “John Doe”。 接下来,我们使用 Null 合并操作符 ?? 来获取一个非空值。如果 name 不为 null,则 result 的…...
【Docker】docker部署conda并激活环境
原文作者:我辈李想 版权声明:文章原创,转载时请务必加上原文超链接、作者信息和本声明。 文章目录 前言一、新建dockerfile文件二、使用build创建镜像1.报错:Your shell has not been properly configured to use conda activate.…...
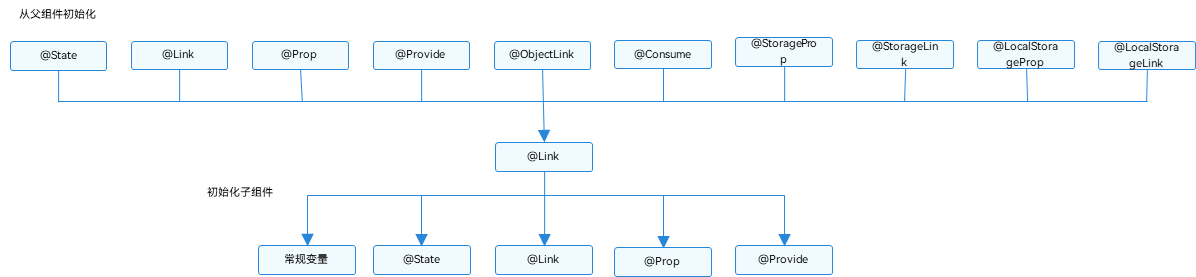
HarmonyOS@Link装饰器:父子双向同步
Link装饰器:父子双向同步 子组件中被Link装饰的变量与其父组件中对应的数据源建立双向数据绑定。 说明 从API version 9开始,该装饰器支持在ArkTS卡片中使用。 概述 Link装饰的变量与其父组件中的数据源共享相同的值。 装饰器使用规则说明 Link变…...
【idea】idea插件编写教程,博主原创idea插件 欢迎下载
前言:经常使用Objects.equals(a,b)方法的同学 应该或多或少都会因为粗心而传错参, 例如日常开发中 我们使用Objects.equals去比较 status(入参),statusEnum(枚举), 很容易忘记statusEnum.getCode() 或 statusEnum.getVaule() ,再比…...
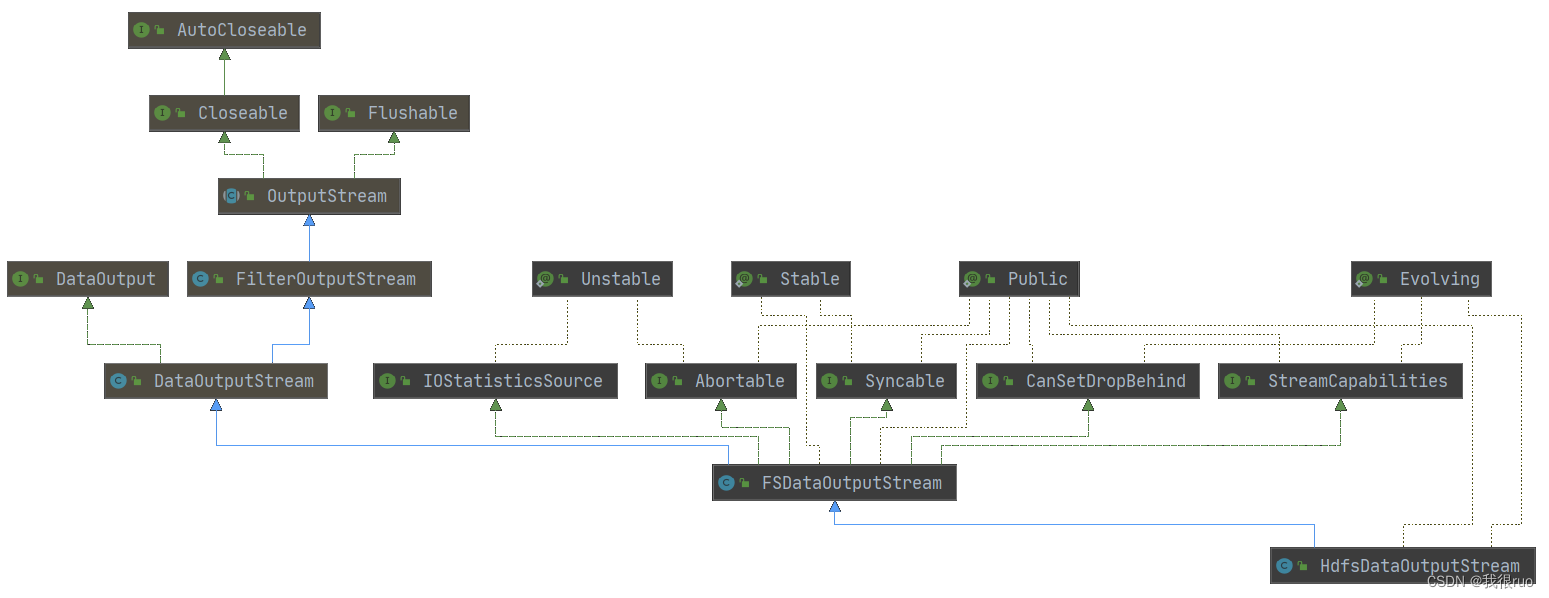
深入理解 Hadoop (四)HDFS源码剖析
HDFS 集群启动脚本 start-dfs.sh 分析 启动 HDFS 集群总共会涉及到的角色会有 namenode, datanode, zkfc, journalnode, secondaryName 共五种角色。 JournalNode 核心工作和启动流程源码剖析 // 启动 JournalNode 的核心业务方法 public void start() throws IOException …...
【Vue3+React18+TS4】1-1 : 课程介绍与学习指南
本书目录:点击进入 一、为什么做这样一门课程? 二、本门课的亮点有哪些? 2.1、轻松驾驭 2.2、体系系统 2.3、高效快捷 2.4、融合贯通 三、课程内容包括哪些? 四、项目实战 《在线考勤系统》 五、课适合哪些同学? 一、为什么做这样一门课程? 近十年内前端…...

Nacos与Eureka的区别详解
Nacos与Eureka的区别详解 在微服务架构中,服务注册与发现是核心组件之一,它们允许服务实例在启动时自动注册,并且能被其他服务发现,从而实现服务之间的互相通信。Nacos和Eureka都是现代微服务体系中广泛使用的服务注册与发现工具。本文将深入分析二者的区别,并为您提供一…...
【算法刷题】Day28
文章目录 1. 买卖股票的最佳时机 III题干:算法原理:1. 状态表示:2. 状态转移方程3. 初始化4. 填表顺序5. 返回值 代码: 2. Z 字形变换题干:算法原理:1. 模拟2. 找规律 代码: 1. 买卖股票的最佳时…...
深入了解pnpm:一种高效的包管理工具
✨专栏介绍 在当今数字化时代,Web应用程序已经成为了人们生活和工作中不可或缺的一部分。而要构建出令人印象深刻且功能强大的Web应用程序,就需要掌握一系列前端技术。前端技术涵盖了HTML、CSS和JavaScript等核心技术,以及各种框架、库和工具…...
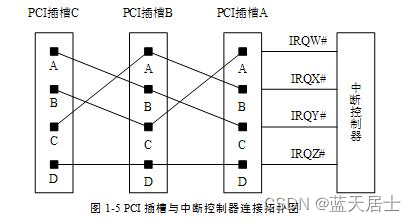
QEMU源码全解析 —— PCI设备模拟(1)
接前一篇文章: 1. PCI设备简介 PCI是用来连接外设的一种局部(local)总线,其主要功能是连接外部设备。PCI总线规范在20世纪90年代提出以后,其逐渐取代了其它各种总线,被各种处理器所支持。直到现在…...
Vue-10、Vue键盘事件
1、vue中常见的按键别名 回车 ---------enter <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>键盘事件</title><!--引入vue--><script type"text/javascript" src"h…...
胡圆圆的暑期实习经验分享
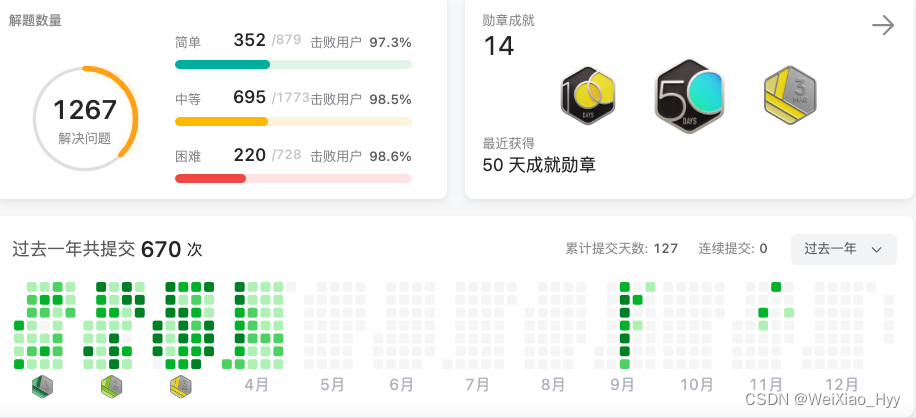
背景 实验室一般是在研究生二年级的时候会放实习,在以后的日子就是自己完成毕业工作要求,基本上不再涉及实验室的活了,目前是一月份也是开始准备暑期实习的好时间。实验室每年这个时候都会有学长学姐组织暑期实习经验分享,本着不…...
基于uniapp封装的table组件
数据格式 tableData: [{elcInfo: [{tableData:[1,293021.1,293021.1,293021.1,293021.1,]}]},{elcInfo: [{tableData:[1,293021.1,293021.1,293021.1,293021.1,]}]},{elcInfo: [{tableData:[1,293021.1,293021.1,293021.1,293021.1,]}]},/* {title: "2",elcInfo: [{…...
Git删除远程仓库某次提交记录后的所有提交
1、鼠标右键->git bash here,然后cd切换到代码目录; 2、git log查看提交记录,获取commit id 3、git reset commit id(commit id指要保留的最新的提交记录id) 4、git push --force,强制push 如果出现…...
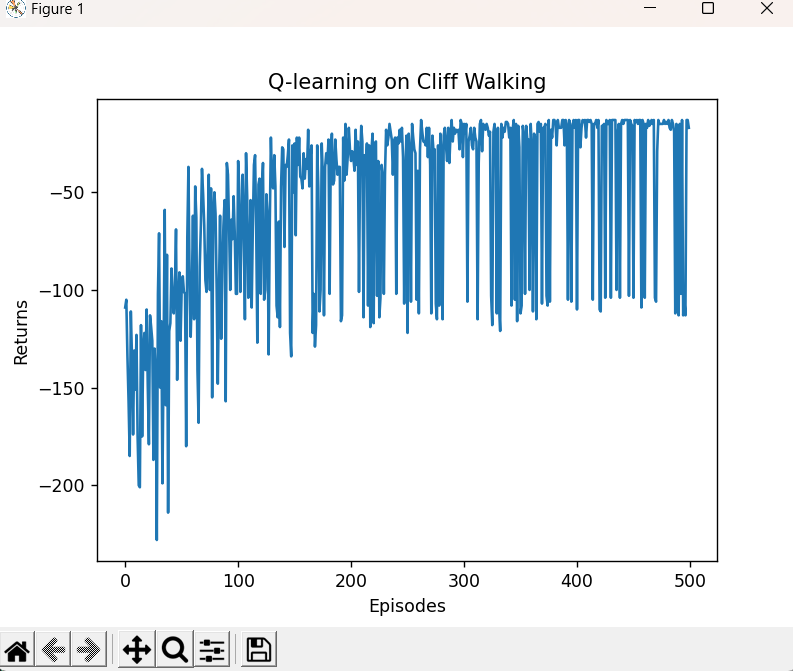
强化学习10——免模型控制Q-learning算法
Q-learning算法 主要思路 由于 V π ( s ) ∑ a ∈ A π ( a ∣ s ) Q π ( s , a ) V_\pi(s)\sum_{a\in A}\pi(a\mid s)Q_\pi(s,a) Vπ(s)∑a∈Aπ(a∣s)Qπ(s,a) ,当我们直接预测动作价值函数,在决策中选择Q值最大即动作价值最大的动作&…...
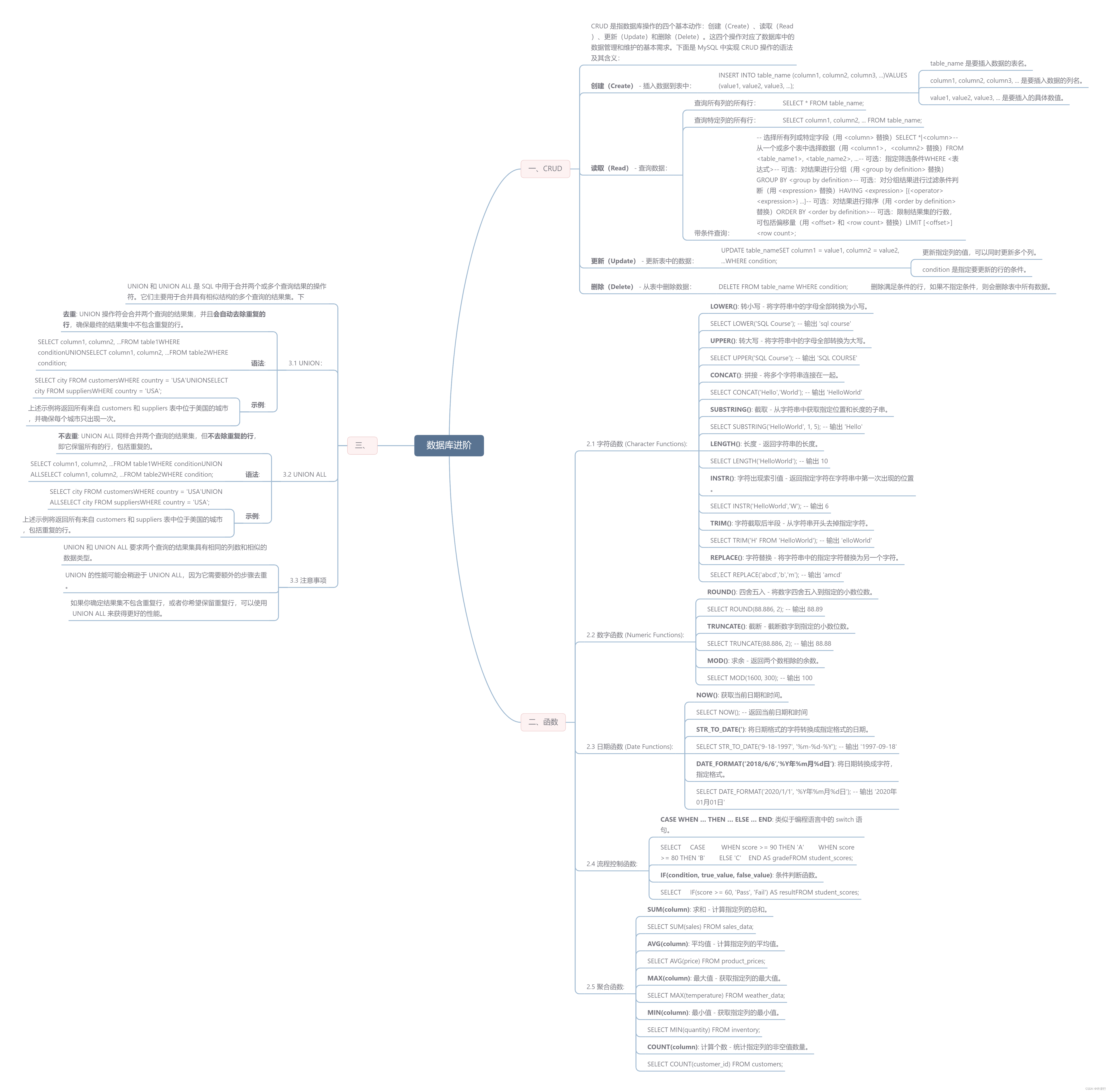
【数据库】CRUD常用函数UNION 和 UNION ALL
文章目录 一、CRUD二、函数2.1 字符函数 (Character Functions):2.2 数字函数 (Numeric Functions):2.3 日期函数 (Date Functions):2.4 流程控制函数:2.5 聚合函数: 三、UNION 和 UNION ALL3.1 UNION:3.2 UNION ALL3.3 注意事项 一、CRUD CRUD 是指数据库操作的四…...

Adding Conditional Control to Text-to-Image Diffusion Models——【论文笔记】
本文发表于ICCV2023 论文地址:ICCV 2023 Open Access Repository (thecvf.com) 官方实现代码:lllyasviel/ControlNet: Let us control diffusion models! (github.com) Abstract 论文提出了一种神经网络架构ControlNet,可以将空间条件控制添加到大型…...

Python与人工智能
Python 是一种广泛用于人工智能(AI)开发的编程语言。Python具有简洁的语法和强大的库支持,使其成为数据科学、机器学习和深度学习的理想选择。 Python中有许多库可以帮助实现人工智能,其中最流行的包括TensorFlow和PyTorch。这些…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
