php 数组中的元素进行排列组合
需求背景:计算出数组['A','B','C','D']各种排列组合,希望得到的是数据如下图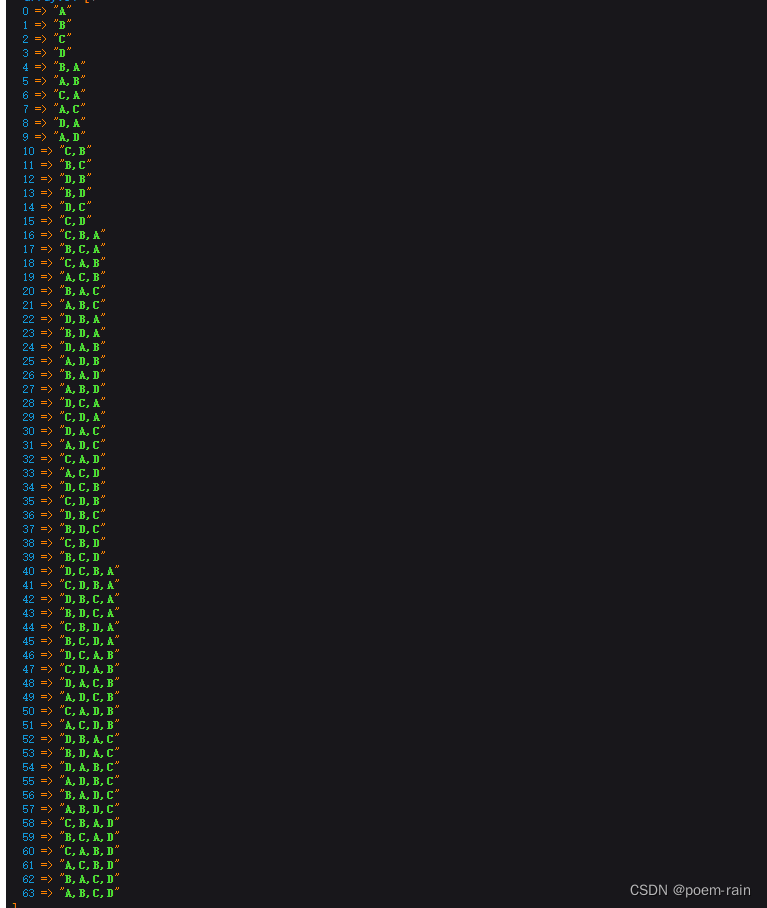
直接上代码:
private function finish_combination($array, &$groupResult = [], $splite = ','){$result = [];$finish_result = [];$this->diffArrayItems($array, $result);foreach ($result as $value) {$items = $this->array_combination($value, $splite);if (!isset($groupResult[count($value)])) $groupResult[count($value)] = [];$groupResult[count($value)] = array_merge($groupResult[count($value)], $items);$finish_result = array_merge($finish_result, $items);}return $finish_result;}
// 不同数组的值进行排列组合例如:['A','B','C'],排列如何出所有的可能性private function array_combination($arr, $splite = ','){$len = count($arr);if ($len == 1) {return $arr;}$result = array();for ($i = 0; $i < $len; $i++) {$tmp_arr = $arr;unset($tmp_arr[$i]);$tmp_arr = array_values($tmp_arr);$tmp_result = $this->array_combination($tmp_arr, $splite);foreach ($tmp_result as $val) {$val .= $splite . $arr[$i];$result[] = $val;}}return $result;}private function getCombinations($input, $length, $start = 0, $current = array(), &$result = array()){if (count($current) === $length) {$result[] = $current;return;}for ($i = $start; $i < count($input); $i++) {$current[] = $input[$i];$this->getCombinations($input, $length, $i + 1, $current, $result);array_pop($current);}}
// 获取不同个数的数组例如['A'],['B'],['C'],['D'],['A''B'],['A''c']......['A', 'B', 'C', 'D']private function diffArrayItems($input, &$result){for ($i = 1; $i <= count($input); $i++) {$this->getCombinations($input, $i, 0, array(), $result);}}//直接调用
$result = $this->finish_combination(['A', 'B', 'C', 'D']);
var_dump($result);// 排列组合了所有的数据后,一般情况下,我们都想着验证下个数是否正确,
例如:
取 1 个元素的排列组合数为 P(4, 1) = 4! / (4 - 1)! = 4! / 3! = 4
取 2 个元素的排列组合数为 P(4, 2) = 4! / (4 - 2)! = 4! / 2! = 12
取 3 个元素的排列组合数为 P(4, 3) = 4! / (4 - 3)! = 4! / 1! = 24
取 4 个元素的排列组合数为 P(4, 4) = 4! / (4 - 4)! = 4! / 0! = 24
下面就需要另外一个函数
//此方法需要开启GMP扩展
private function nP($n){$sum = 0;for ($i = 1; $i <= $n; $i++) {$sum += gmp_fact($n) / gmp_fact($n - $i);}return intval($sum);}
// 然后直接调用
echo $this->nP(count('A', 'B', 'C', 'D']));相关文章:

php 数组中的元素进行排列组合
需求背景:计算出数组[A,B,C,D]各种排列组合,希望得到的是数据如下图 直接上代码: private function finish_combination($array, &$groupResult [], $splite ,){$result [];$finish_result [];$this->diffArrayItems($array, $…...
Python从入门到网络爬虫(OS模块详解)
前言 本章介绍python自带模块os,os为操作系统 operating system 的简写,意为python与电脑的交互。os 模块提供了非常丰富的方法用来处理文件和目录。通过使用 os 模块,一方面可以方便地与操作系统进行交互,另一方面页可以极大增强…...

人机交互不是人机融合智能
一、人机交互和人机融合智能是两个不同的概念 人机交互是指人类与计算机之间的信息交流和操作方式,包括输入和输出界面、交互技术、用户体验等方面。人机交互的目标是提供用户友好的界面和自然的交互方式,使人类能够与计算机更加高效地进行沟通和协作。 …...

RabbitMQ解决消息丢失以及重复消费问题
文章目录 1、概念2、基于ACK/NACK机制2.1 基于Spring AMQP框架整合ACK/NACK机制2.2 测试消费失败1.02.3 测试结果1.02.4 测试MQ宕机2.5 测试结果2.0 3、RabbitMQ 如何实现幂等性设计3.1 幂等服务设计思路3.1.1 通过雪花算法生成分布式唯一ID3.1.2 通过枚举类,设计Me…...

docker 安装redis集群
一、准备6台机器 二、6台机器分别拉取镜像: docker pull redis三、6台机器分别建立挂载文件夹 mkdir -p /home/redis/data四、6台机器分别执行容器操作 docker run --restartalways -d --name redis-node-1 --net host --privilegedtrue -v /home/redis/data:/da…...

锂电池制造设备中分布式IO模块优势
在“碳达峰、碳中和”目标推动下,新能源汽车当下发展势头正盛,而纯电动车的核心部件则是:锂电池。动力型锂电池作为新能源汽车核心零部件,其发展与新能源汽车行业息息相关,迎来广阔的市场空间。 为何采用I/O模块&#…...

Android Room数据库升级Migration解决方案
一、介绍 Android Room 是 Android 官方提供的一个轻量级数据库框架,用于在 Android 应用程序中管理数据持久性。它简化了数据库访问,提供了更安全、更快速的数据存储方式,并使得数据操作更加便捷。 二、Room的特点(八股文可以参考) 以下是…...

离线安装docker和docker-compose
1.下载 docker Index of linux/static/stable/x86_64/ docker-compose Overview of installing Docker Compose | Docker Docs 2.docker /etc/systemd/system/docker.service [Unit] DescriptionDocker Application Container Engine Documentationhttps://docs.docker.…...

奇怪的事情记录:外置网卡和外置显示器不兼容
身为程序员,不应该对世界上的稀奇古怪的事情感到惊讶(毕竟,大部分都是程序员自己搞出来的)。 外置网卡和外置显示器不兼容 mbp2019intel版,win10,外接有线网卡,平时用得很好,接上外…...
【大数据进阶第三阶段之Hive学习笔记】Hive基础入门
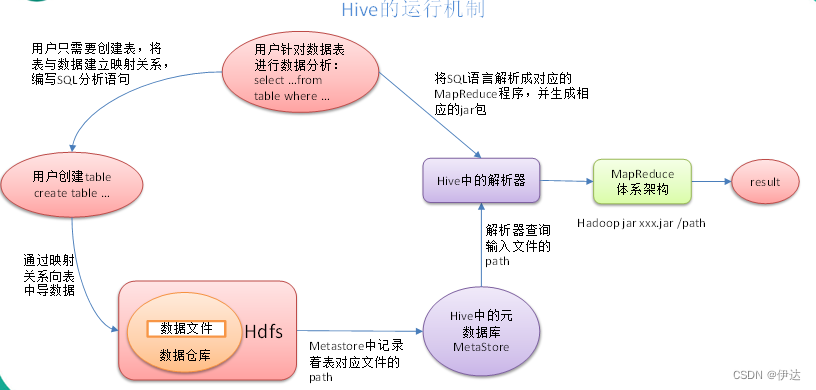
目录 1、什么是Hive 2、Hive的优缺点 2.1、 优点 2.2、 缺点 2.2.1、Hive的HQL表达能力有限 2.2.2、Hive的效率比较低 3、Hive架构原理 3.1、用户接口:Client 3.2、元数据:Metastore 3.3、Hadoop 3.4、驱动器:Driver Hive运行机制…...

第三代量子计算机交付,中国芯片开辟新道路,光刻机难挡中国芯
日前安徽本源量子宣布第三代超导量子计算系统正式上线,这是中国最先进的量子计算机,计算量子比特已达到72个,在全球已居于较为领先的水平,这对于中国芯片在原来的硅基芯片受到光刻机阻碍无疑是巨大的鼓舞。 据悉本源量子的第一代、…...
react native中使用tailwind并配置自动补全
使用的第三方库是tailwind-react-native-classnames,同类的也有tailwind-rn,但是我更喜欢前者官方demo: import { View, Text } from react-native; import tw from twrnc;const MyComponent () > (<View style{twp-4 android:pt-2 b…...
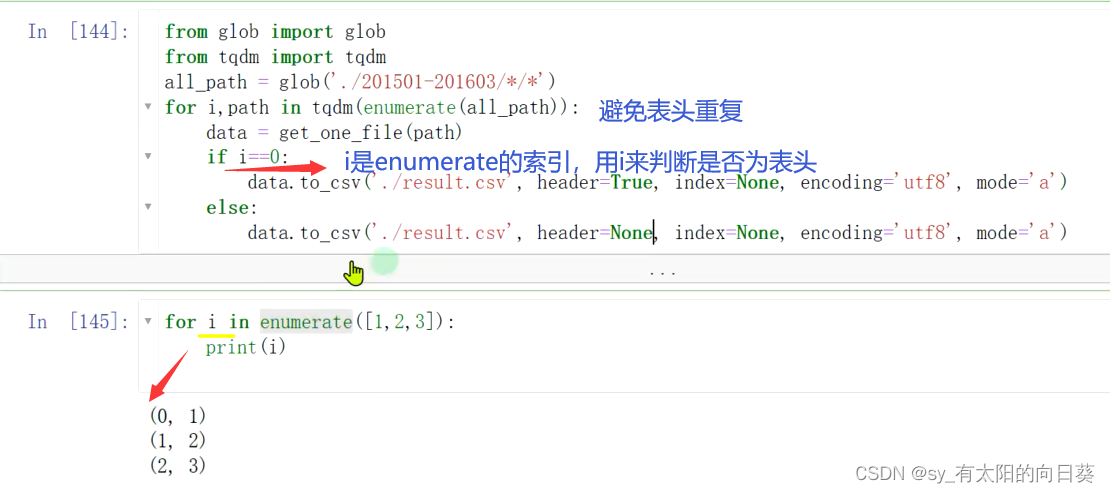
数据分析——火车信息
任务目标 任务 1、整理火车发车信息数据,结果的表格形式为: 2、并输出最终的发车信息表 难点 1、多文件 一个文件夹,多个月的发车信息,一个excel,放一天的发车情况 2、数据表的格式特殊 如何分析表是一个难点 数…...
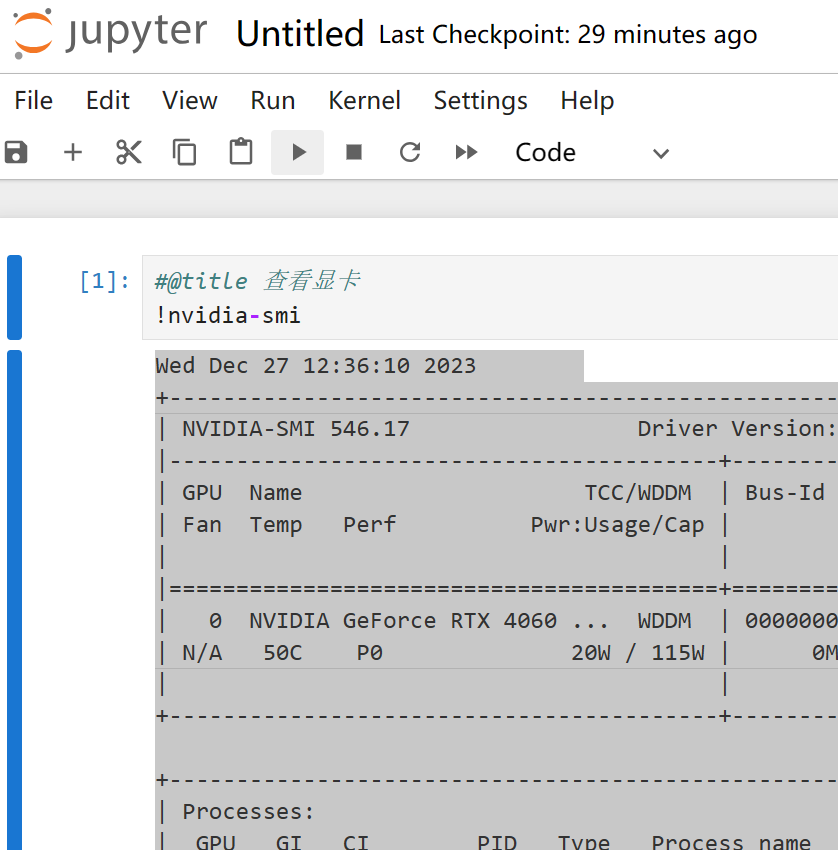
Bert-vits2最终版Bert-vits2-2.3云端训练和推理(Colab免费GPU算力平台)
对于深度学习初学者来说,JupyterNoteBook的脚本运行形式显然更加友好,依托Python语言的跨平台特性,JupyterNoteBook既可以在本地线下环境运行,也可以在线上服务器上运行。GoogleColab作为免费GPU算力平台的执牛耳者,更…...
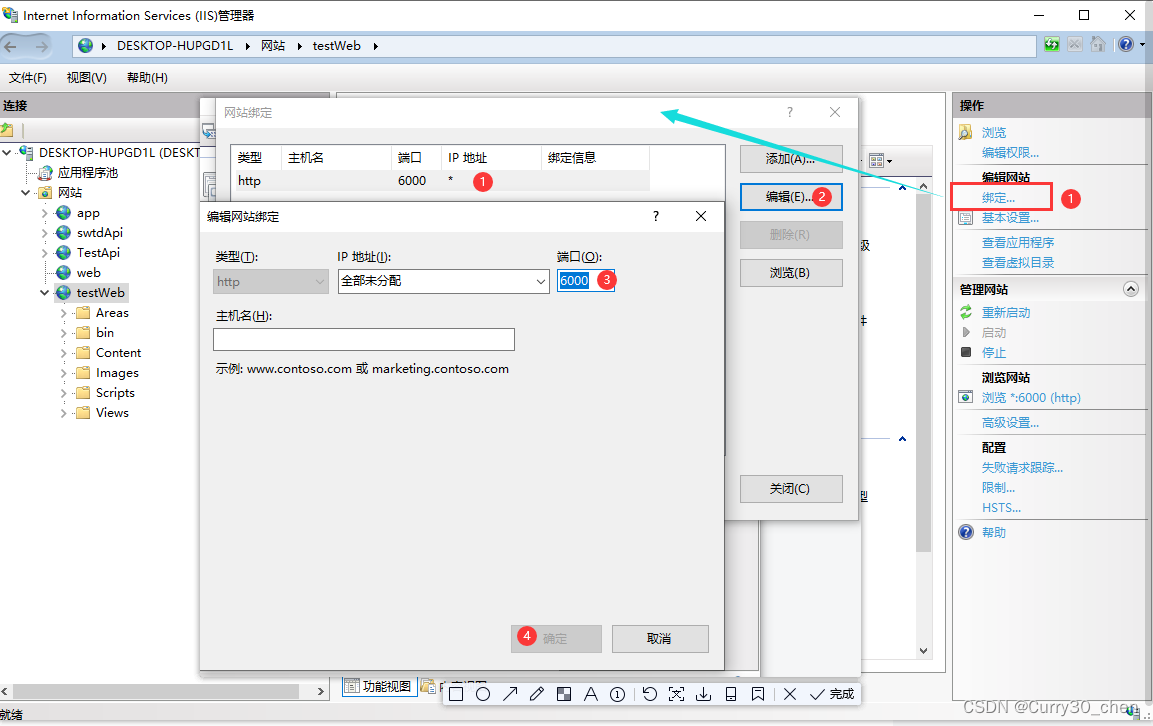
Asp .Net Web应用程序(.Net Framework4.8)网站发布到IIS
开启IIS 如果已开启跳过这步 打开控制面板-程序 打开IIS 发布Web程序(.Net Framework 4.8 web网页) 进入IIS管理器新建一个应用池 新建一个网站 网站创建完毕 为文件夹添加访问权限 如果不添加访问权限,运行时将会得到如下错误 设置权限 勾…...

vue element plus Typography 排版
我们对字体进行统一规范,力求在各个操作系统下都有最佳展示效果。 字体# 字号# LevelFont SizeDemoSupplementary text12px Extra SmallBuild with ElementBody (small)13px SmallBuild with ElementBody14px BaseBuild with ElementSmall Title16px MediumBuild w…...

理论U3 决策树
文章目录 一、决策树算法1、基本思想2、构成1)节点3)有向边/分支 3、分类步骤1)第1步-决策树生成/学习、训练2)第2步-分类/测试 4、算法关键 二、信息论基础1、概念2、信息量3、信息熵: 二、ID3 (Iterative Dichotomis…...

Redis 常用操作
一、Redis常用的5种数据类型 字符串(String):最基本的数据类型,可以存储字符串、整数或浮点数。哈希(Hash):键值对的集合,可以在一个哈希数据结构中存储多个字段和值。列表…...

c# 使用Null合并操作符例子
在这个示例中,我们定义了两个字符串变量 name 和 defaultName。变量 name 被赋值为 null,而变量 defaultName 被赋值为 “John Doe”。 接下来,我们使用 Null 合并操作符 ?? 来获取一个非空值。如果 name 不为 null,则 result 的…...
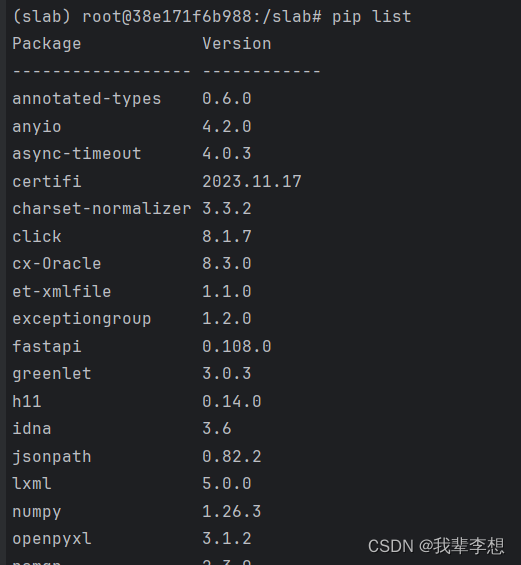
【Docker】docker部署conda并激活环境
原文作者:我辈李想 版权声明:文章原创,转载时请务必加上原文超链接、作者信息和本声明。 文章目录 前言一、新建dockerfile文件二、使用build创建镜像1.报错:Your shell has not been properly configured to use conda activate.…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
