【问题解决】web页面html锚点定位后内容被遮挡问题解决【暗锚】
正常的锚点跳转
a标签的href填写目标元素的id即可
<a href="#my_target">to div1</a> <div id="my_target">div1</div>
内容被顶栏遮挡示例
但是当id所在元素被嵌套多层flex和relative布局之后,跳转后部分内容会被遮挡。

解决办法(暗锚)
将锚点所在元素(不一定是div,也可以是其他标签)定义为relative相对布局。将锚点target定义为absolute绝对布局,并且添加top对应需要跳转位置离顶部的距离。
<div class="my-anchor"><span id="target-home"></span><span id="target-features"></span><span id="target-roadmap"></span>
</div>
.my-anchor{...position: relative;
}
#target-home{position: absolute;top:83px;
}
#target-features{position: absolute;top:883px;
}
#target-roadmap{position: absolute;top:2403px;
}
现在跳转后页面顶部内容不会被遮挡,由于span锚点在直观上不可见,所以称之为暗锚。
用vue3做web时遇到了该问题,记录一次解决过程,如有其他问题可以提问讨论。
相关文章:

【问题解决】web页面html锚点定位后内容被遮挡问题解决【暗锚】
正常的锚点跳转 a标签的href填写目标元素的id即可 <a href"#my_target">to div1</a> <div id"my_target">div1</div> 内容被顶栏遮挡示例 但是当id所在元素被嵌套多层flex和relative布局之后,跳转后部分内容会被遮挡…...

easyui datagrid无数据时显示无数据
这里写自定义目录标题 需求解决办法 需求 使用datagrid显示记录时,结果查询记录数为0,此时需要显示无数据。 示例代码 <table id"dg"></table>$(#dg).datagrid({url:datagrid_data.json,columns:[[{field:code,title:Code,widt…...

动态规划python简单例子-斐波那契数列
def fibonacci(n):dp [0, 1] [0] * (n - 1) # 初始化动态规划数组for i in range(2, n 1):dp[i] dp[i - 1] dp[i - 2] # 计算斐波那契数列的第 i 项print(dp)return dp[n] # 返回斐波那契数列的第 n 项# 示例用法 n 10 # 计算斐波那契数列的第 10 项 result fibonac…...
免 费 搭 建 多模式商城:b2b2c、o2o、直播带货一网打尽
鸿鹄云商 b2b2c产品概述 【b2b2c平台】,以传统电商行业为基石,鸿鹄云商支持“商家入驻平台自营”多运营模式,积极打造“全新市场,全新 模式”企业级b2b2c电商平台,致力干助力各行/互联网创业腾飞并获取更多的收益。从消…...

Python AttributeError: ‘NoneType‘ object has no attribute ‘shape‘如何解决
Python AttributeError: ‘NoneType‘ object has no attribute ‘shape‘ 运行出现上述错误,这个错误表示某个图像对象为 NoneType ,没有 shape 属性。通常情况下,这是因为 OpenCV 没有能够正确地加载图像,导致无法访问图像数据。…...
vue3自定义确认密码匹配验证规则
// 自定义确认密码匹配验证规则 const matchPassword (rules:any, value:any, callback:any) > {if (value ! addData.payPwd) {callback(new Error(两次密码输入不一致!))} else {callback()} }const rules reactive({payPwd: [{ required: true, message: &q…...

岗位所处定位,岗位职责
电子产品所需岗位:pcb设计电路板,fpga,嵌入式,应用层(前后端,移动端)。 PCB 岗位职责:1.负责器件.工程或者项目与技术验证类的PCB板设计工作;2.协助项目中部分模块的PCB(…...

2024阿里云服务器配置推荐方案
阿里云服务器配置怎么选择合适?CPU内存、公网带宽和ECS实例规格怎么选择合适?阿里云服务器网aliyunfuwuqi.com建议根据实际使用场景选择,例如企业网站后台、自建数据库、企业OA、ERP等办公系统、线下IDC直接映射、高性能计算和大游戏并发&…...

OceanBase原生分布式数据库
1.历史背景 在Java Web项目中,常常使用免费开源的MySQL数据库存储业务数据,按业界经验MySQL单库超过多大数据体量,或单表超过几百万条数据后就会出现查询变慢的情况,单实例数据库只能扩展物理资源(CPU、内存),来提升查…...

首次使用go-admin
go-admin 1.1 拉取 拉去后端代码 git clone https://github.com/go-admin-team/go-admin.git拉取前端代码 git clone gitgithub.com:go-admin-team/go-admin-ui.git 1.2 编译 cd ./go-admingo mod tidygo build1.3 配置文件的修改 这里可以可以根据自己的需要进行自定义两…...
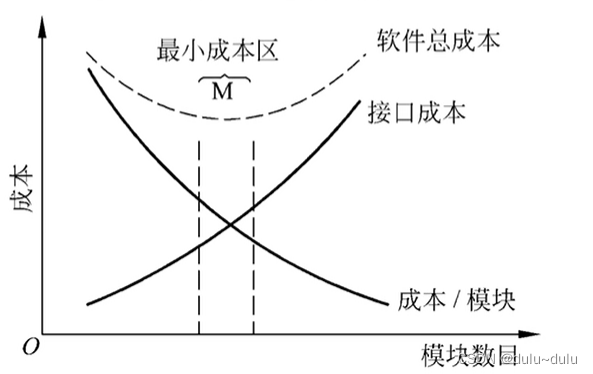
软件工程概论---内聚性和耦合性
目录 一.耦合性 1.内容耦合 2.公共耦合 4.控制耦合 5.标记耦合(特征耦合) 6.数据耦合 7.非直接耦合 二.内聚性 1.偶然内聚 2.逻辑内聚 3.时间内聚 4.过程内聚 5.通信内聚 6.顺序内聚 7.功能内聚 一.耦合性 耦合性是指软件结构中模块相互…...

纯血鸿蒙「扩圈」100天,酝酿已久的突围
坦白讲,去年参加华为开发者大会看到HarmonyOS NEXT(仅运行鸿蒙原生应用,所以也称作「纯血鸿蒙」)的时候,小雷也没料想到鸿蒙原生应用生态的发展速度会如此之快。 9月25日,华为正式对外宣布启动HarmonyOS NE…...
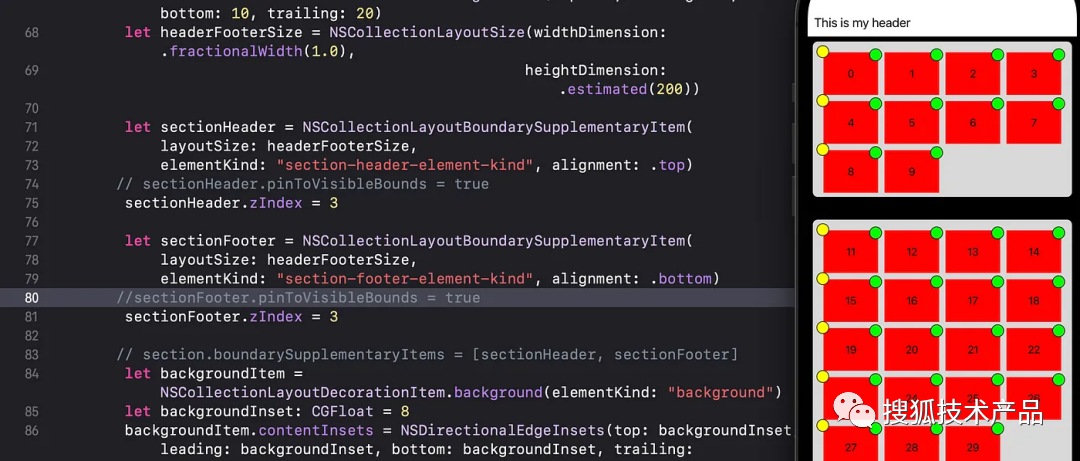
UICollection Compositional Layout全详解
本文字数:8325字 预计阅读时间:45分钟 01 Collection View Layout全详解 UICollectionView在iOS中是构建复杂布局的强大工具。iOS13中引入的 UICollectionViewCompositionalLayout为创建自定义布局提供了全新的可能性。本文将深入探讨Compositional Lay…...

单例模式的模板
参考了网上的一些单例模式,自己也写一个模板。 要点: 线程安全性单例对象的唯一性 #include <mutex> //在模板类 Singleton 中,可以定义单例模式的实现细节 template <typename T> class Singleton { public://通过删除拷贝构造…...

C#基础-空处理
在c#中,值对象是没有办法赋值为null的。比如说,你想要定义一个布尔值,你的赋值数据要么得是true、要么就得是false,默认情况下我们永远没可能给这个布尔赋值为null,即使只是对这个变量进行声明而不初始化数据ÿ…...

测试平台开发vue组件化重构前端代码
基于 springbootvue 的测试平台开发 继续更新(人在魔都 T_T)。 这期其实并不是一个详细的开发过程记录,主要还是针对本次前端重构来聊聊几个关注点。 目前重构的总进度在80%,重构完的页面没什么变化,再回顾一下。 一…...

龍运当头--html做一个中国火龙祝大家龙年大吉
🐉效果展示 🐉HTML展示 <body> <!-- partial:index.partial.html --> <svg><defs><g id=...
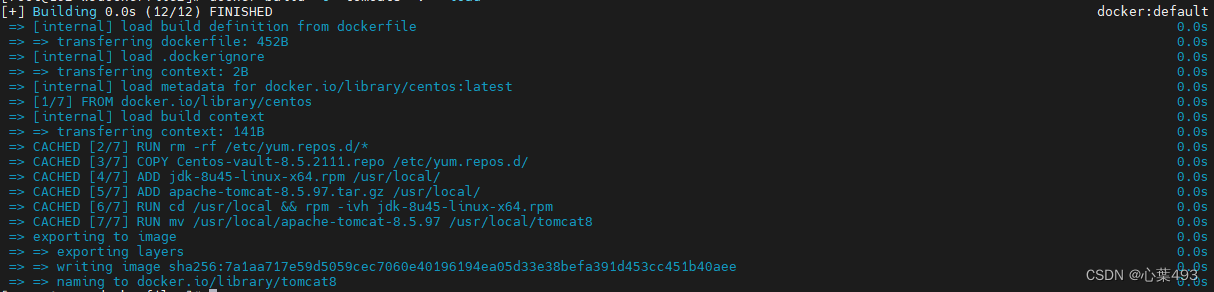
Dockerfile语法和简单镜像构建
Dockerfile是一个用于定义Docker镜像的文本文件,包含了一系列的指令和参数,用于指示Docker在构建镜像时应该执行哪些操作,例如基于哪个基础镜像、复制哪些文件到镜像中、运行哪些命令等。 Dockerfile文件的内容主要有几个部分组成,…...

uniapp使用wxml-to-canvas开发小程序保存canvas图片
微信小程序官方解决方案:wxml-to-canvas 使用wxml-to-canvas要知道一些前提条件 1、只能画view,text,image 2、每个元素必须要设置宽高 3、默认是flex布局,可以通过flexDirection: "column"来改变排列方式 4、文字 必…...

关于数据库切换的麻烦
背景介绍 现项目使用了两个数据源,分别为A、B,两个数据库的数据结构并不相同,数据库A是用来做查询一些基本信息的,数据库B是用来保留业务操作数据的。后端是在mapper层用DS注解来区分哪些地方用数据库A,而哪些地方用数…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
